Similar presentations:
Кинематика точки (Лекция 1, кафедра теоретической механики )
1.
Новосибирский Государственный Архитектурно-СтроительныйУниверситет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
КИНЕМАТИКА
ЛЕКЦИЯ № 1
КИНЕМАТИКА ТОЧКИ
Кафедра теоретической механики
2.
План лекцииВведение
Способы задания движения
Траектория
Скорость
Ускорение
Частные случаи движения
Заключение
3.
ВведениеМы изучили первый раздел курса ТМ - статику.
Основной результат:
F F
ТЕЛО, СИЛЫ : ( F1 ,..., F1 )
n
n
( F1 ,..., F1 ) 0 Fk 0, M 0 Fk 0
k 1
k 1
1
2
F3
Fn
Если уравнения равновесия не выполнены, то тело
будет двигаться! Каким образом?
Ответ на этот вопрос будет дан в третьей части
курса – в динамике.
Вторая часть курса – кинематика, нужна для того,
чтобы разобраться с самим движением.
Причины движения (т.е. СИЛЫ) нас в кинематике
интересовать не будут!
4.
ВведениеИтак:
Кинематика изучает геометрические свойства
движения тел (без учета действующих на них сил).
Основные ее задачи:
1. Научиться задавать движение тел
2. По заданному движению тел определять их
кинематические характеристики (траекторию,
скорость, ускорение, ….)
Замечание. Есть еще и обратная задача - по
заданным кинематическим характеристикам тела
определять закон его движения.
Решать эти задачи мы начнем с простейшего тела –
точки.
5.
Цель лекции:Изучить кинематику точки.
6.
Способы задания движения точки, траектория1. В прямоугольной декартовой системе Oxyz
z
r (t )
k
O
j
i
x
x x(t ), y y (t ), z z (t )
M
y
z
x
y
координатный способ
r (t ) x(t )i y (t ) j z (t )k
r r (t ) векторный способ
Траектория точки – геометрическое место
положений, занимаемых ею при движении( или след,
который она оставит, если ее покрасить; или еще:
годограф ее радиус-вектора ).
Замечание. Не путать с другим “определением”:
траектория – это линия, по которой движется точка.
Траектория может быть лишь часть этой линии!!!
7.
Определение траекторииПример. Точка двигалась в плоскости Oxy в течение
10 секунд. Определить ее траекторию, если
x(t ) 2t; y(t ) 12t
2
Решение. Заданные уравнения
определяют траекторию в
параметрическом виде. Для
получения явного вида y=y(x)
исключим параметр t. Получим:
y 3x 2
y
x
O 10 20
t x / 2 y 3x . t 0,10 x 0,20
2
Ответ:
Траектория – часть параболы
y 3x , x 0,20
2
8.
Способы задания движения точки (продолжение)1. В естественной системе координат
A –O
Пусть линия AB, по которой
+
движется точка, известна. Тогда
s
положение точки М на линии
M
B можно определить введя
естественную координату s.
s OM ; s s(t )
Такой способ задания называется естественным.
Система координат с криволинейной осью AB
называется естественной системой координат.
Само уравнение s=s(t) называется законом движения
точки вдоль траектории.
Замечание. Так и определяют движение поездов и
автомобилей, вводя километраж на дорогах.
9.
Способы задания движения точки (продолжение)Вопрос. Дуговая координата s и
путь S, пройденный точкой одно и
– O
+
то же?
s
Ответ. НЕТ, например для
автомобиля, двигавшегося по
маршруту O M1 M ; S s1 (s1 s)
Замечание. При решении задач механики
используются и другие системы координат:
полярная, цилиндрическая, сферическая….
M
M1
10.
Скорость точкиr r (t t ) r (t )
r
v ср
v lim
t
dr
v
скорость
dt
M (t )
z
r dr
t dt
A
r (t )
v
r
M (t t )
v cp
r (t t )
B
точки
O
x
Скорость точки равна производной от ее радиусавектора по времени.
Направлена скорость – по касательной к
траектории точки в сторону ее движения.
y
11.
Проекции скорости точкиВ системе
Oxyz:
A
dr
v
r x i y j z k
dt
v x x , v y y v z z
В естественной системе:
M (t )
z
r (t )
v
r
M (t t )
v cp
r (t t )
B
O
x
dr
dr ds
v
;
dt
ds dt
dr
единичный вектор касательной
ds
ds
v
s касательная скорость
dt
t
v v ; v v; s(t) s(0) x 2 y 2 z 2 dt
0
y
12.
Пример определения скоростиПример. Точка движется по дуге
окружности радиуса R=20см по
закону s=20sin( t). Определить
величину и направление
скорости для t=5c.
Решение.
s(5) 20 sin 5 0 точка
v (t) 20 cos 5 20
v(5) 20
и
направлено
v(5)
в
в
– O +
положении
сторону
" "
О
13.
Ускорение точкиv1
M (t1 )
v
aср
M (t1 t )
v2
v v2 v1 - приращение вектора скорости за время Δt
v - среднее ускорение – изменение
a cp
скорости в единицу времени
t
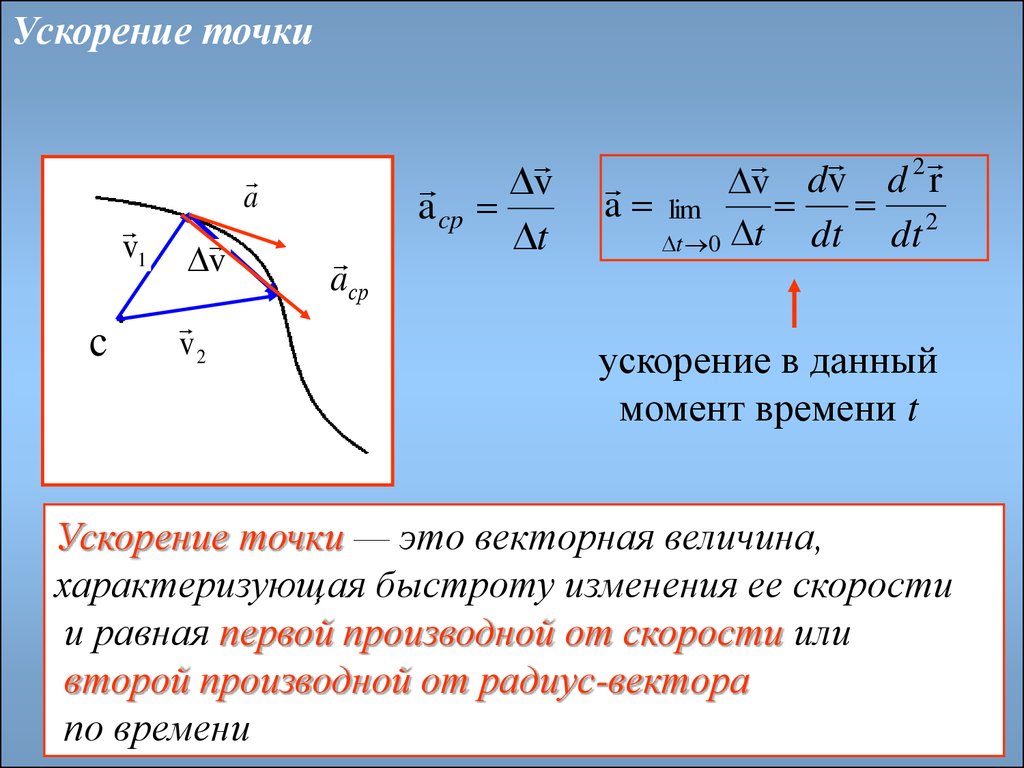
14.
Ускорение точкиv1
c
a
v
v2
a cp
aср
v
t
2
v dv d r
2
a lim
dt dt
t 0 t
ускорение в данный
момент времени t
Ускорение точки — это векторная величина,
характеризующая быстроту изменения ее скорости
и равная первой производной от скорости или
второй производной от радиус-вектора
по времени
15.
Проекции ускорения точки1. В системе Oxyz
вектор скорости
v
vx i v y j vzk
вектор ускорения
a
a x i a y j a zk
d v
v x i v y j v z k
a x i a y j a zk
dt
a x v x x
a y v y y
a z v z z
16.
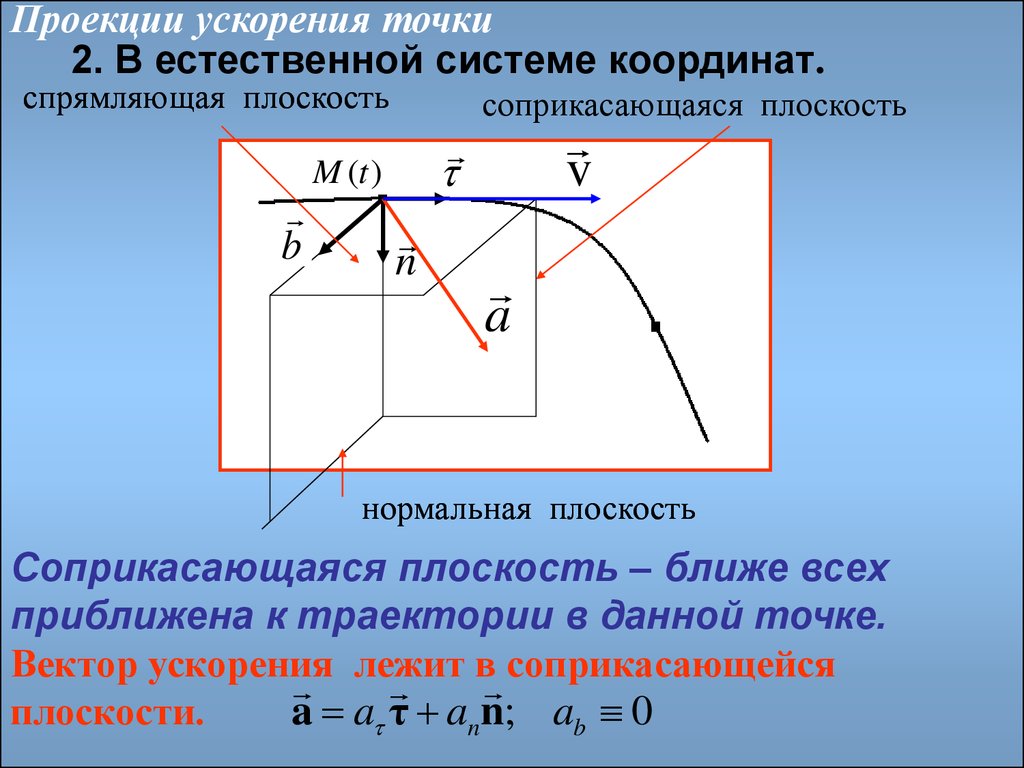
Проекции ускорения точки2. В естественной системе координат.
спрямляющая плоскость
b
соприкасающаяся плоскость
v
M (t )
n
a
нормальная плоскость
Соприкасающаяся плоскость – ближе всех
приближена к траектории в данной точке.
Вектор ускорения лежит в соприкасающейся
плоскости.
a a τ ann; ab 0
17.
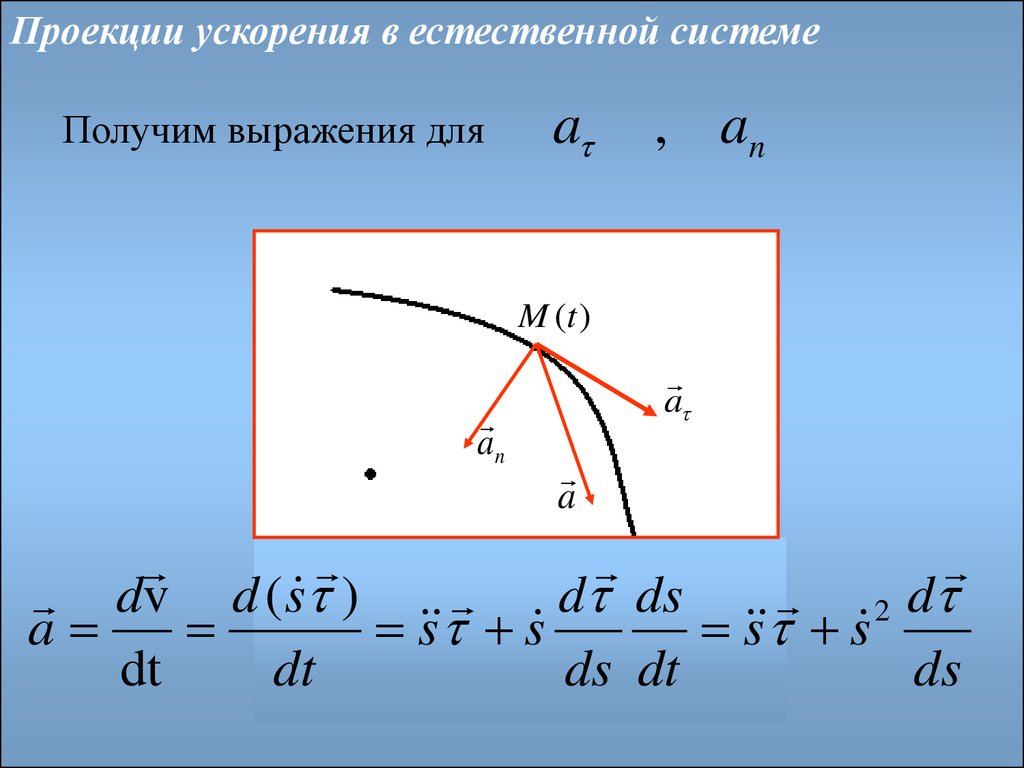
Проекции ускорения в естественной системеПолучим выражения для
a
, an
M (t )
an
a
a
dv d ( s )
2 d
d ds
a
s s
s s
dt
dt
ds dt
ds
18.
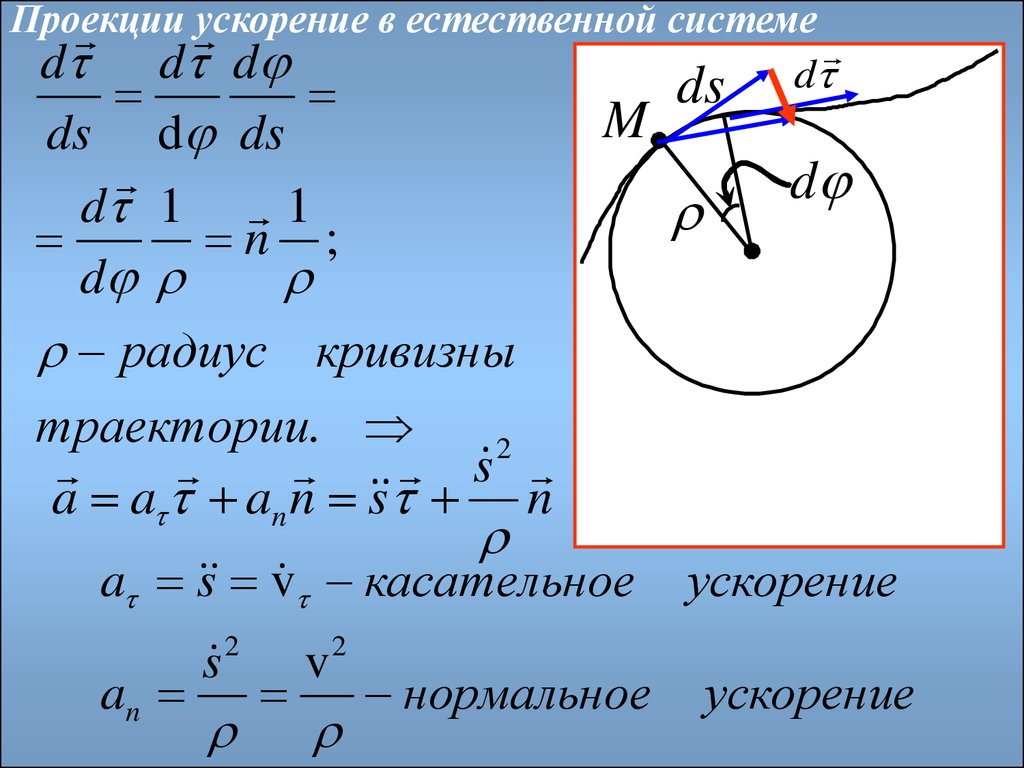
Проекцииускорение в естественной системе
d d d
ds d
M
ds d ds
d 1 1
n ;
d
радиус кривизны
траектории.
2
s
a a an n s n
a s v касательное
an
s 2
v
2
нормальное
d
ускорение
ускорение
19.
Проекции ускорения в естественной системеa s v касательное
an
s
2
–
v
2
О
ускорение
нормальное
ускорение
+ s(t)
M
an
n
a
a
v
20.
Механический смысл касательного и нормальногоускорения
a s v ; an
s
2
v
2
Касательное ускорение ответственно за изменение
вектора скорости по модулю.
Нормальное ускорение ответственно за изменение
скорости по направлению.
21.
Пример.v
A
a
B
Преступник в пункте A сел в машину в 12-00 и
поехал по дороге с начальной скоростью 100км/час.
Пункт перехвата B находится в 50 км от пункта A.
Известно, что он ехал все время так, что
Помогите поймать преступника.
v a
22.
Простейшие движения точкиРавномерное движение
a 0
v const
v t1
v t1 v t2 v t3
v t 2
Уравнение движения и нач. условия:
s v 0
s 0 s0
Закон движения:
s s0 v 0t
v t3
v const
a 0
an 0
a 0
an 0
23.
Простейшие движения точкиЕсли
Ускоренное движения:
Замедленное движения:
a 0
v a 0
v a 0
v 0
a 0
a 0
v 0
Равнопеременное движение
a const
Уравнение движения и нач. условия:
s a
v 0 v 0 s 0 s0
Закон движения:
s s0 v 0t a t 2 2
24.
ЗаключениеЗаключение
Определены основные задачи кинематики.
Рассмотрены способы задания движения точки.
Определена траектория точки.
Определена скорость и ускорение точки.
Определены проекции скорости и
ускорения в прямоугольной декартовой и
естественной системах координат
6. Выяснен механический смысл
касательного и нормального ускорения.
7. Рассмотрены частные случаи движения
точки.
1.
2.
3.
4.
5.
25.
Вопросы для самоконтроля1.Что называется механическим движением
точки?
2. Какой геометрией описывается пространство,
в котором происходит движение тел?
3. Зависит ли расстояние между двумя точками
пространства от выбора системы координат?
4. Что означает однородность пространства и
времени?
5. Что изучает кинематика?
6. Сформулируйте задачи кинематики.
7. Какие способы задания движения
материальной точки существуют?
8. Что такое траектория материальной точки?
9. Что такое скорость материальной точки?
26.
Вопросы для самоконтроля10. Как определяется единичный вектор,
направленный вдоль касательной к
траектории?
11. Что характеризует ускорение?
12. Ускорение это векторная величина или скалярная?
13. Что характеризует тангенциальное ускорение, чему
оно равно и как направлено?
14. Что характеризует нормальное ускорение, чему оно
равно и как направлено?
15. Что такое радиус кривизны траектории?
16. Какое движение точки называется
равнопеременным?
17. Что называется ускорением точки?
18. Какое движение называется равномерным?
27.
Тема следующей лекцииПростейшие движения
твердого тела.























 physics
physics mechanics
mechanics








