Similar presentations:
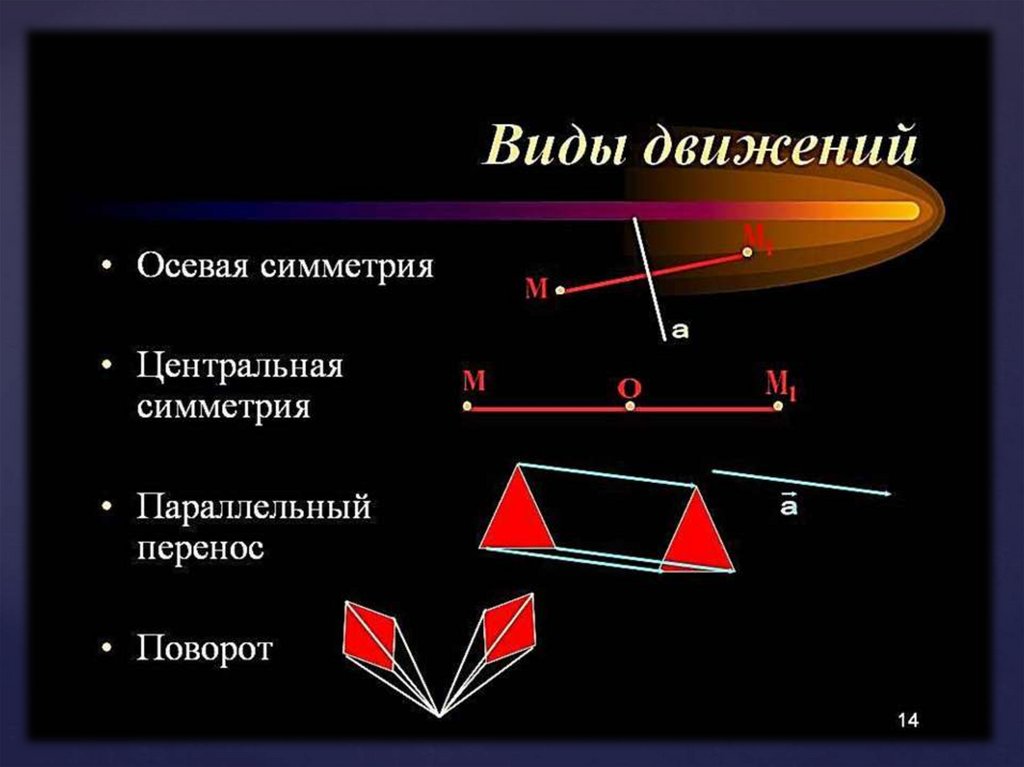
Понятие движения в геометрии
1.
Муниципальное бюджетное общеобразовательное учреждениесредняя школа №1 г. Павлово
Презентация по геометрии
на тему:
«Понятие движения
в геометрии»
Выполнили: учащаяся 9 Б класса
Рыбакина Екатерина.
г. Павлово
Март, 2019 год
2.
СОДЕРЖАНИЕ:Определение движения пространства
Определение симметрии, виды
симметрии.
Осевая симметрия.
Теорема.
3. Симметрия – (от греч.) соразмерность, пропорциональность, одинаковость в расположении частей.
Движение (перемещение) плоскости это отображение плоскости на себя, прикотором сохраняются расстояния
между точками.
Симметрия – (от греч.)
соразмерность, пропорциональность,
одинаковость в расположении частей.
4.
5. Осевой симметрией с осью a называется такое отображение пространства на себя, при котором любая точка M переходит в
симметричную ей точку M1 относительно оси a.Симметрия простейших фигур
6. Докажем , что осевая симметрия является движением. Для этого введём прямоугольную систему координат Oxyz.
7.
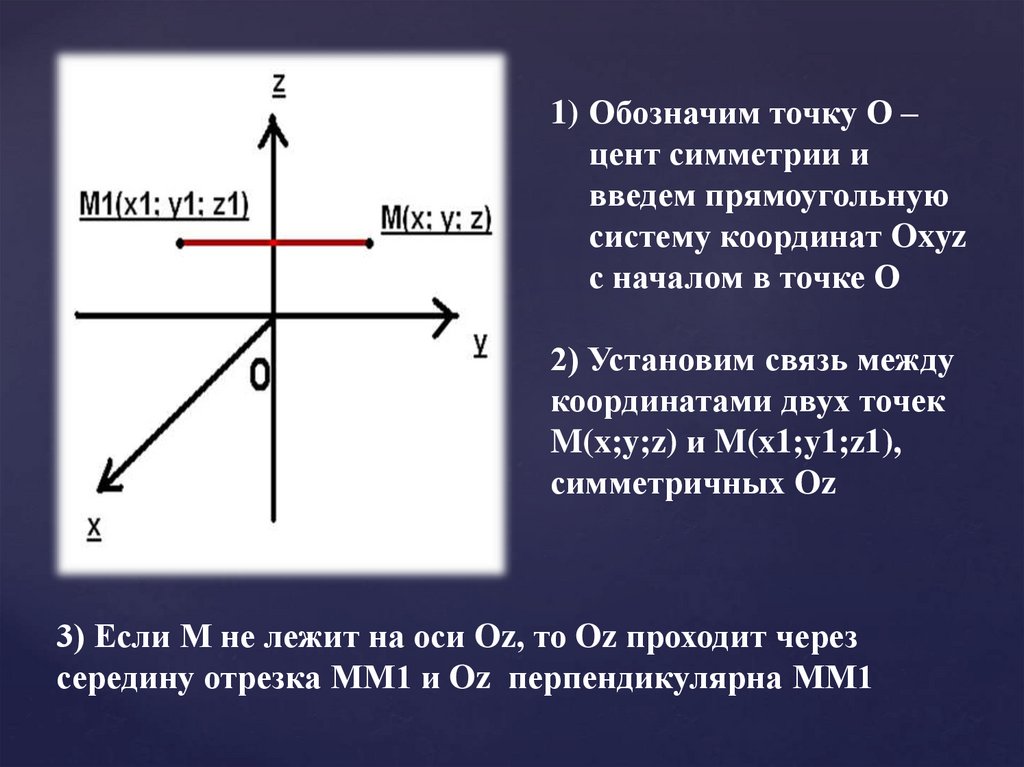
1) Обозначим точку О –цент симметрии и
введем прямоугольную
систему координат Oxyz
с началом в точке О
2) Установим связь между
координатами двух точек
M(x;y;z) и M(x1;y1;z1),
симметричных Oz
3) Если М не лежит на оси Oz, то Oz проходит через
середину отрезка ММ1 и Oz перпендикулярна ММ1
8.
Координаты середины отрезкав пространстве
9.
4) Из первого условия по формуле длякоординат середины отрезка получаем
(x+x1)/2=0 и (y+y1)/2=0, откуда x1=-x; y1=-y
5) Второе условие означает, что аппликаты
(аппликатой точки называется координата
этой точки на оси OZ в прямоугольной
трёхмерной системе координат)
точек М и М1 равны: z1=z
10.
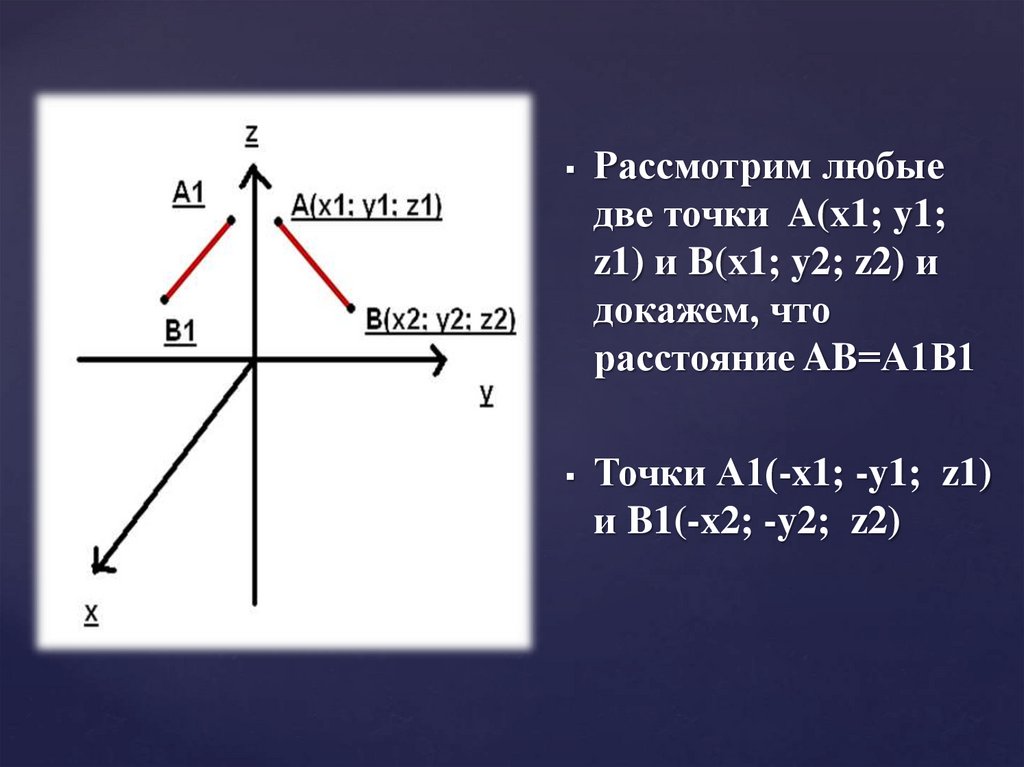
Рассмотрим любыедве точки A(x1; y1;
z1) и B(x1; y2; z2) и
докажем, что
расстояние AB=А1В1
Точки А1(-x1; -y1; z1)
и B1(-x2; -y2; z2)
11. По формуле расстояния между двумя точками находим:
тогда АВ=А1В1,что и требовалось доказать.
12.
Центральная симметрияявляется движением
Теорема:
Доказательство:
Пусть A и B — две произвольные
точки фигуры F.
При симметрии относительно точки O фигуры F
точка A переходит в точку A1, точка B — в точку B1.
Рассмотрим треугольники AOB и A1OB.
1) AO=OA1
2) BO=OB1 (так как A и A1, B и B1 — точки,
симметричные относительно точки O)
3) ∠AOB=∠B1OA1 (как вертикальные)
Следовательно, треугольники AOB и A1OB равны
(по двум сторонам и углу между ними).
Из равенства треугольников следует равенство
соответствующих сторон: AB=A1B1, то есть
расстояние между точками сохраняется, а значит,
преобразование симметрии относительно точки
является движением.
Что и требовалось доказать.











 mathematics
mathematics








