Similar presentations:
Понятие о движении плоскости. Центральная и осевая симметрии. 9 класс
1.
14.04.20239-А,Б,В классы
Геометрия
Тема урока: Понятие о движении
плоскости. Центральная и осевая
симметрии
2.
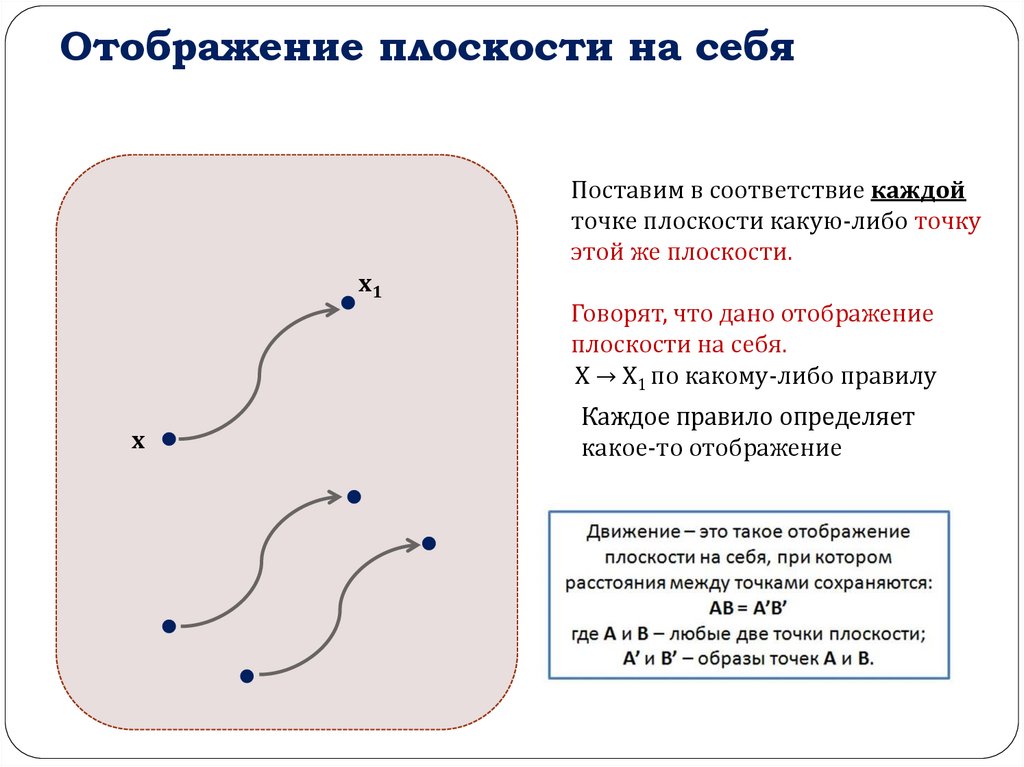
Отображение плоскости на себяПоставим в соответствие каждой
точке плоскости какую-либо точку
этой же плоскости.
х1
х
Говорят, что дано отображение
плоскости на себя.
Х → Х1 по какому-либо правилу
Каждое правило определяет
какое-то отображение
3.
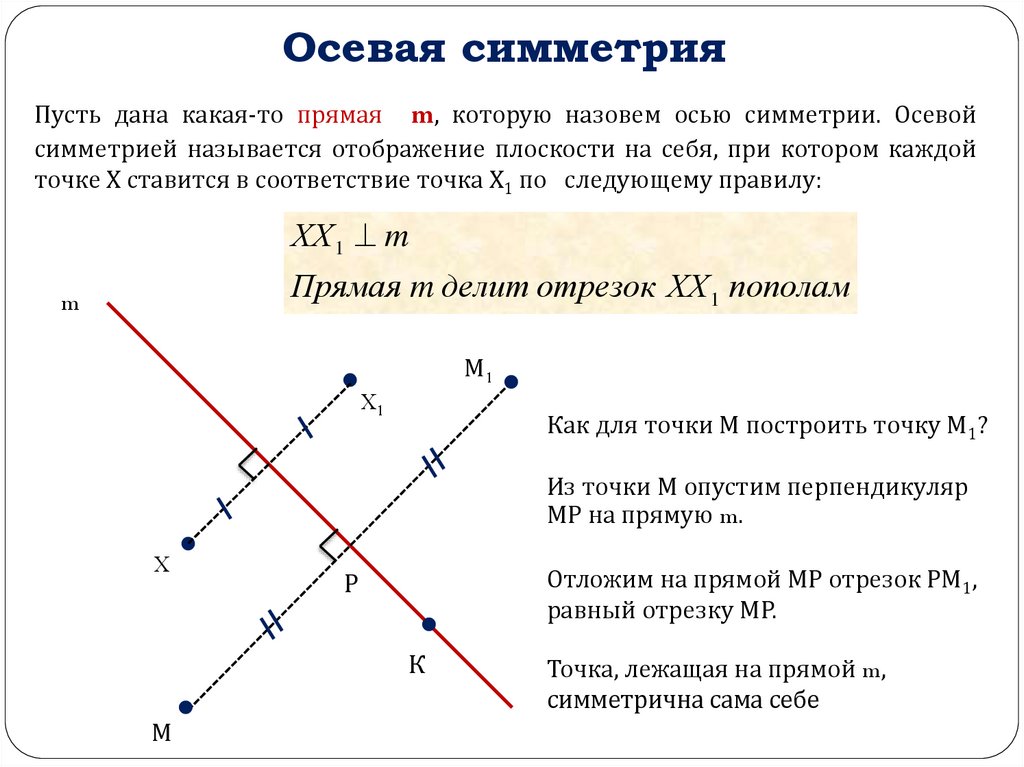
Осевая симметрияПусть дана какая-то прямая m, которую назовем осью симметрии. Осевой
симметрией называется отображение плоскости на себя, при котором каждой
точке Х ставится в соответствие точка Х1 по следующему правилу:
ХХ 1 m
Прямая m делит отрезок ХХ 1 пополам
m
М1
X1
Как для точки М построить точку М1?
Из точки М опустим перпендикуляр
МР на прямую m.
X
Отложим на прямой МР отрезок РМ1,
равный отрезку МР.
Р
К
М
Точка, лежащая на прямой m,
симметрична сама себе
4.
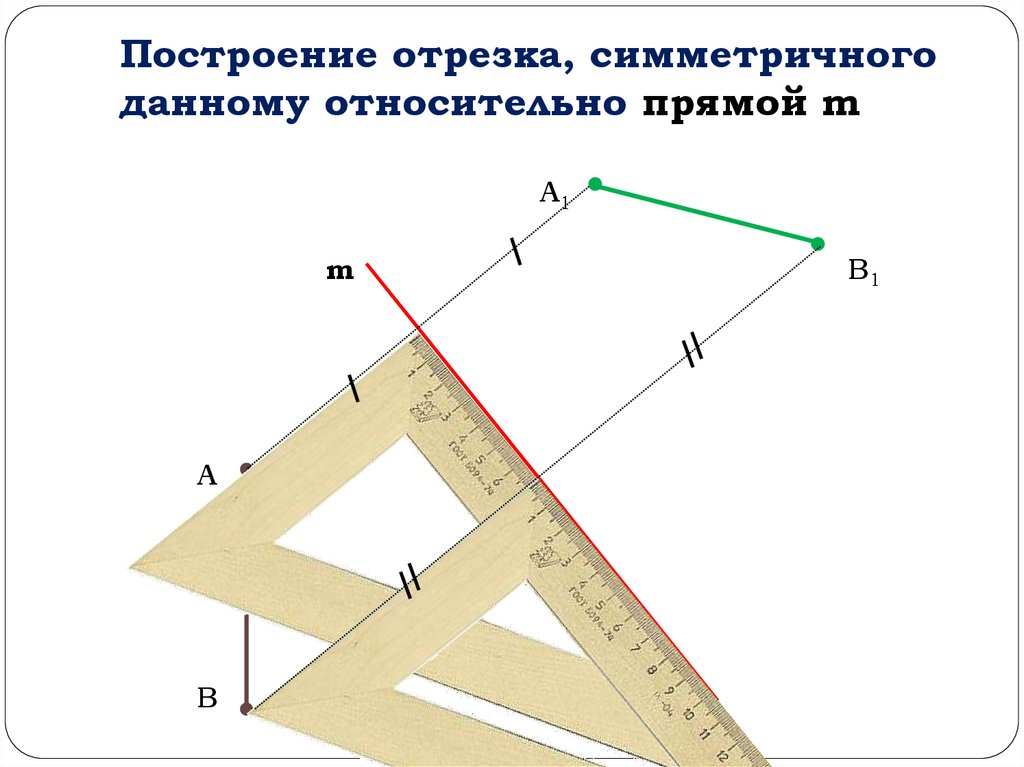
Построение отрезка, симметричногоданному относительно прямой m
A1
m
A
B
B1
5.
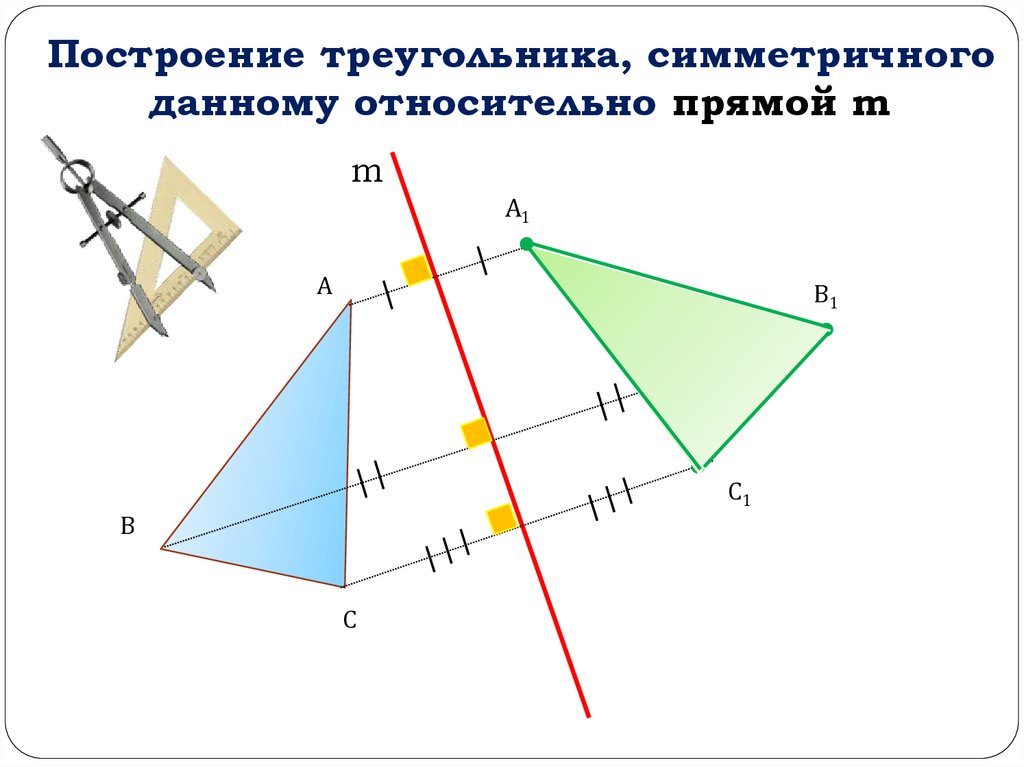
Построение треугольника, симметричногоданному относительно прямой m
m
А1
А
В1
С1
В
С
6.
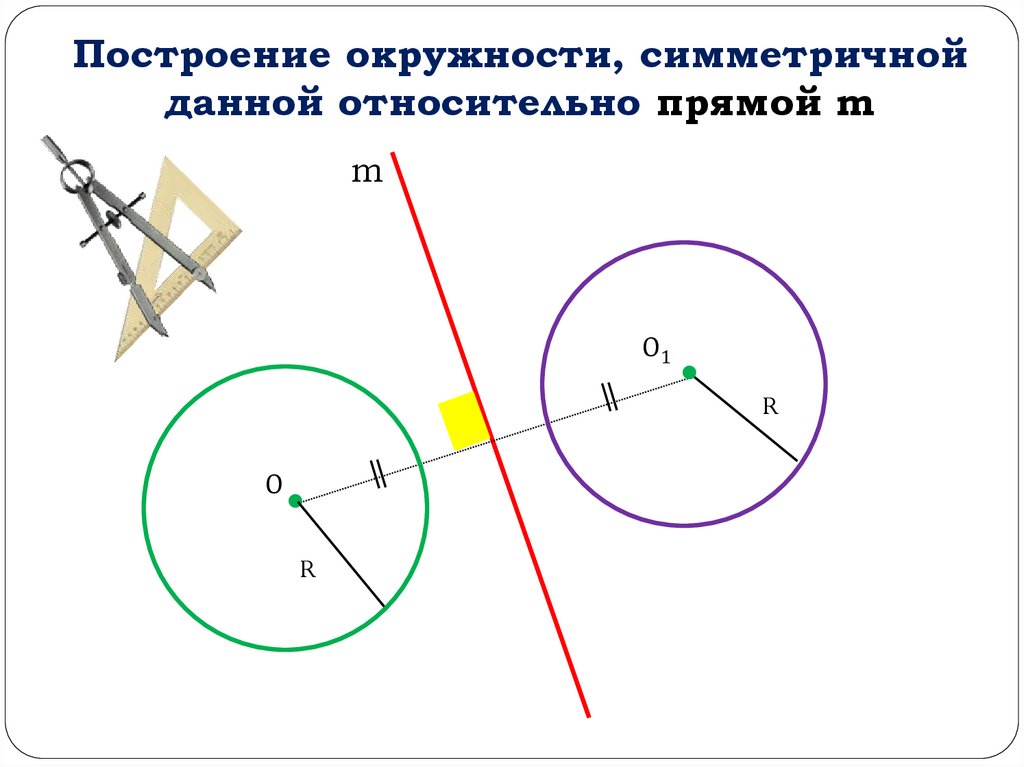
Построение окружности, симметричнойданной относительно прямой m
m
О1
R
O
R
7.
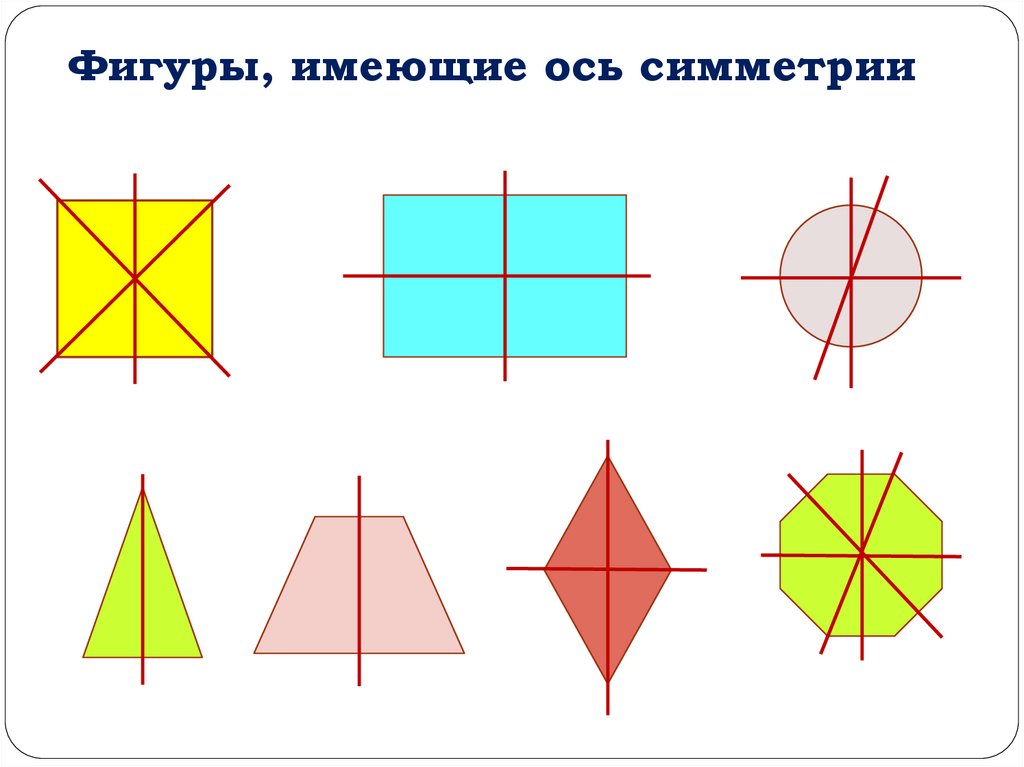
Фигуры, имеющие ось симметрии8.
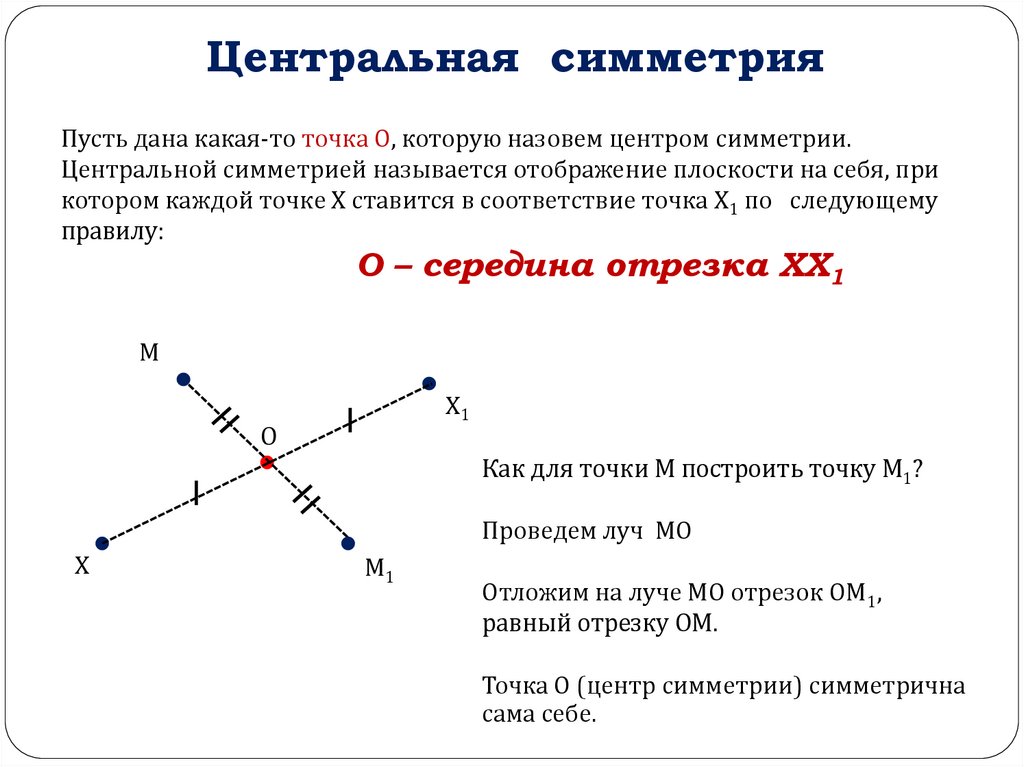
Центральная симметрияПусть дана какая-то точка О, которую назовем центром симметрии.
Центральной симметрией называется отображение плоскости на себя, при
котором каждой точке Х ставится в соответствие точка Х1 по следующему
правилу:
О – середина отрезка ХХ1
М
Х1
О
Как для точки М построить точку М1?
Проведем луч МО
Х
М1
Отложим на луче МО отрезок ОМ1,
равный отрезку ОМ.
Точка О (центр симметрии) симметрична
сама себе.
9.
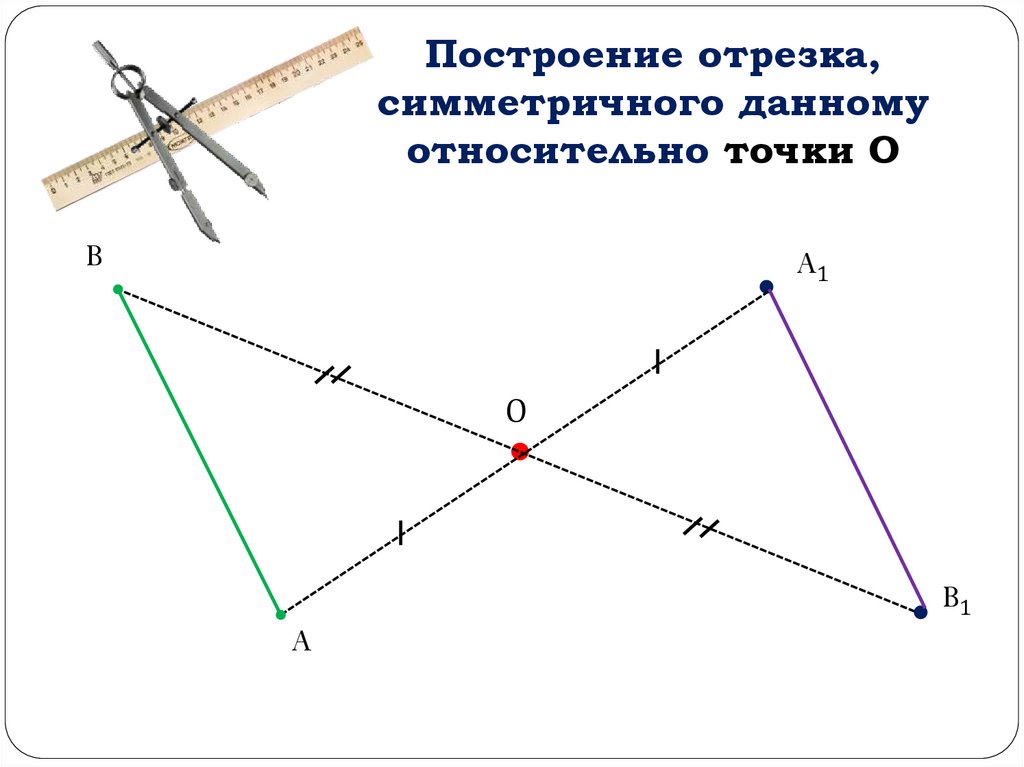
Построение отрезка,симметричного данному
относительно точки О
B
A1
О
B1
A
10.
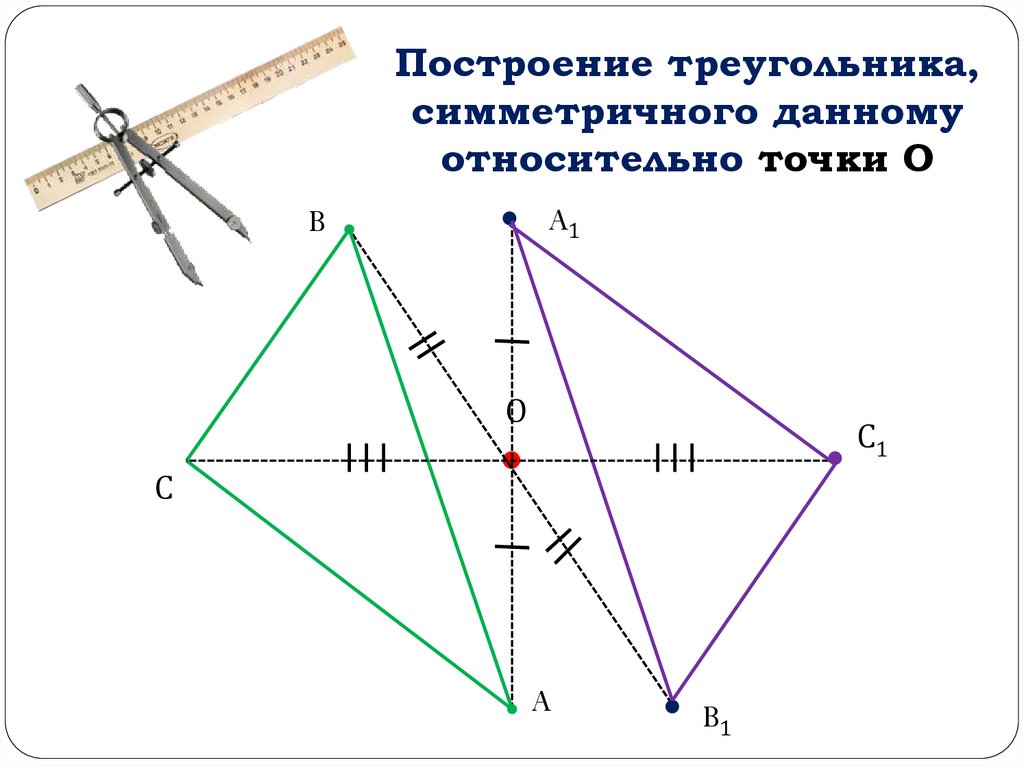
Построение треугольника,симметричного данному
относительно точки О
A1
B
О
С1
С
A
B1
11.
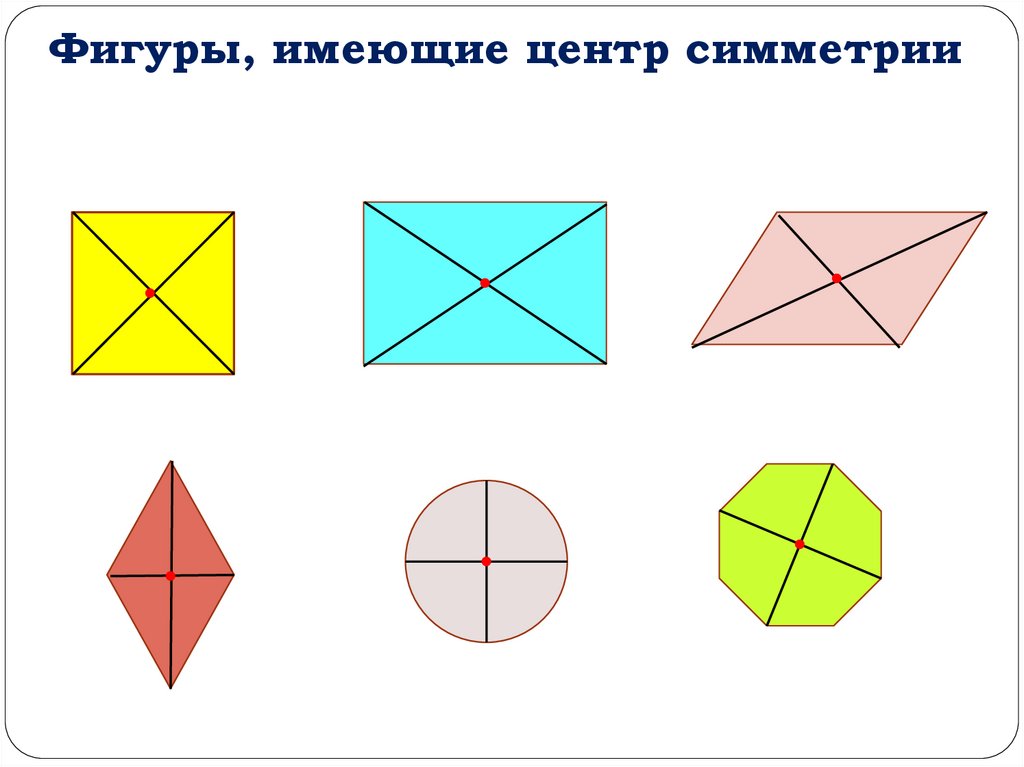
Фигуры, имеющие центр симметрии12.
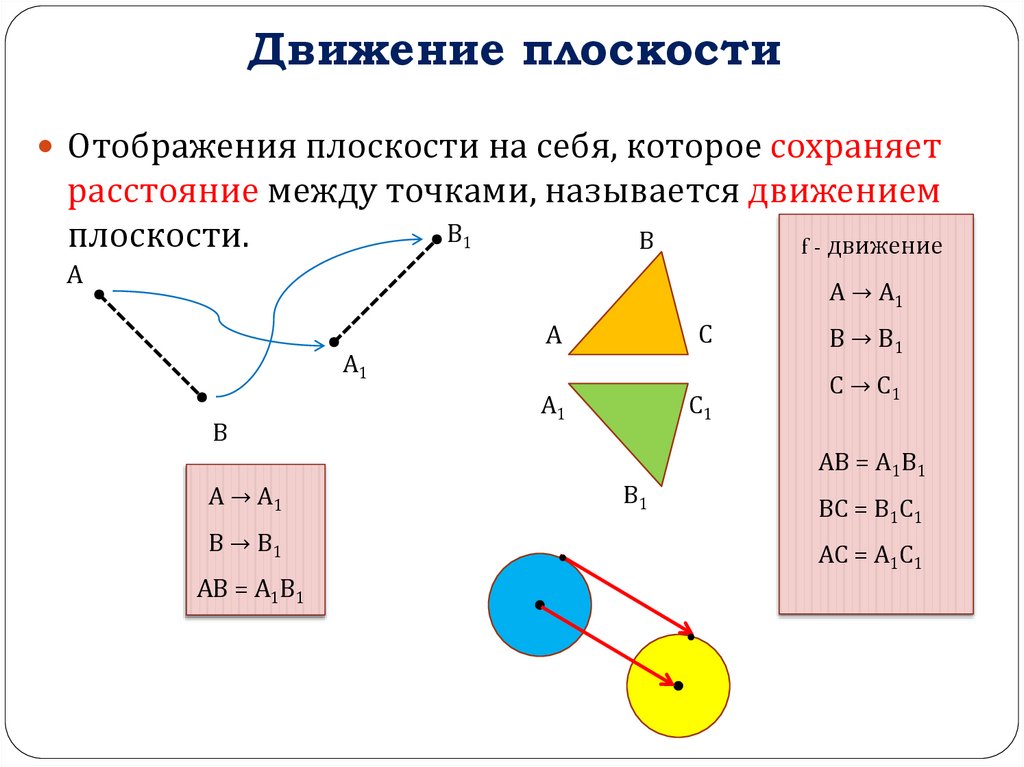
Движение плоскостиОтображения плоскости на себя, которое сохраняет
расстояние между точками, называется движением
В1
плоскости.
В
f - движение
А
А → А1
А1
В
А → А1
В → В1
АВ = А1В1
А
С
А1
С1
В1
В → В1
С → С1
АВ = А1В1
ВС = В1С1
АС = А1С1
13.
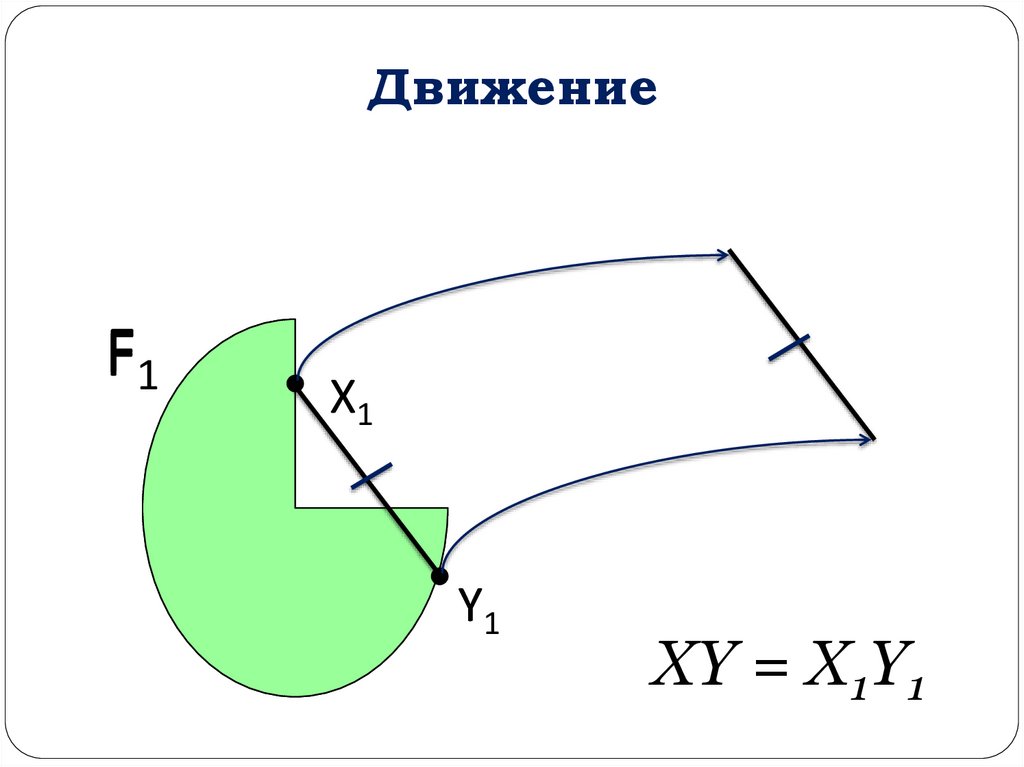
ДвижениеF1
X1
Y1
XY = X1Y1
14.
Теорема. Осевая симметрия - движениеДано: f – осевая симметрия,
прямая m - ось симметрии
Х → Х1
У → У1
Доказать: ХУ = Х1У1
m
X1
У1
К
Z1
Р
X
Z
У
Проведем УУ1 и 1 1 УУ1
XZ X 1Z1
ХYZ Х 1Y1Z1
YZ Y1Z1
Из равенства ХYZ Х 1Y1Z1 ХY Х 1Y1
15.
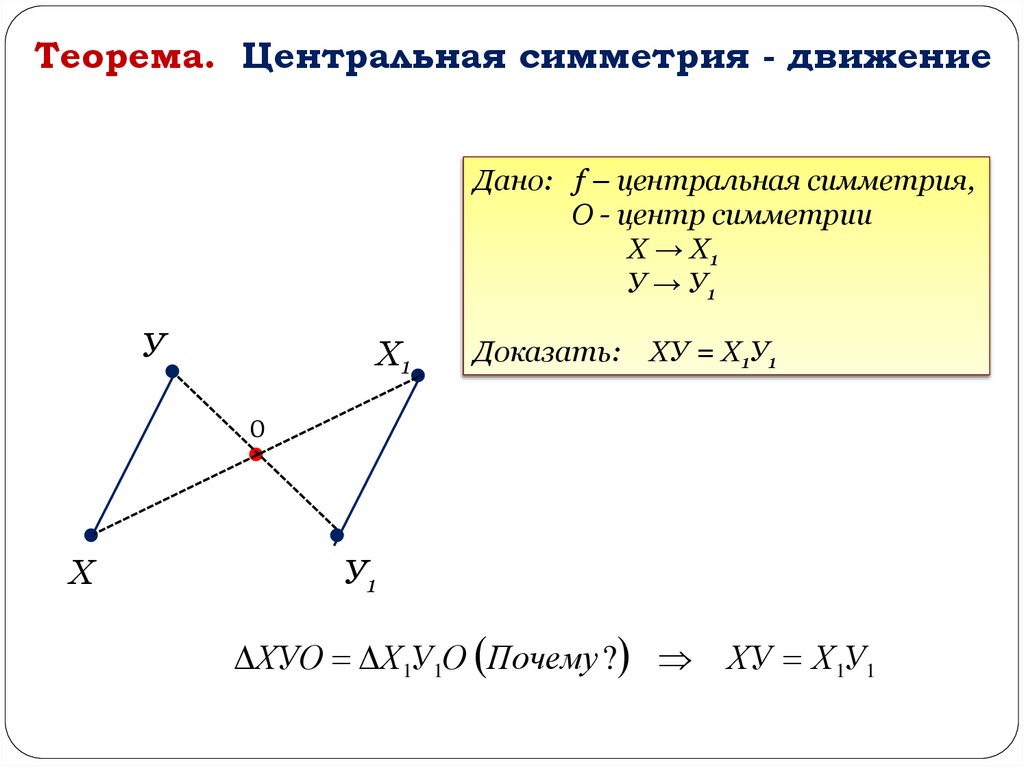
Теорема. Центральная симметрия - движениеДано: f – центральная симметрия,
О - центр симметрии
Х → Х1
У → У1
У
Х1
Доказать: ХУ = Х1У1
О
Х
У1
ХУО Х 1У1О Почему ?
ХУ Х 1У1
16.
Свойства движения1. При движении отрезок отображается на отрезок
Р
А
А1
В
Р1
В1
f движение
A A1 B B1
P AB P P1
Доказать : P1 A1 B1 ( A1 P1 P1 B1 A1 B1 )
f движение
A A1 B B1
AB A1 B1
P P1
AP A1 P1
PB P1 B1
P AB AP PB AB
A1 P1 P1 B1 AP PB AB A1 B1
Получили : A1 P1 P1 B1 A1 B1 P1 A1 B1
17.
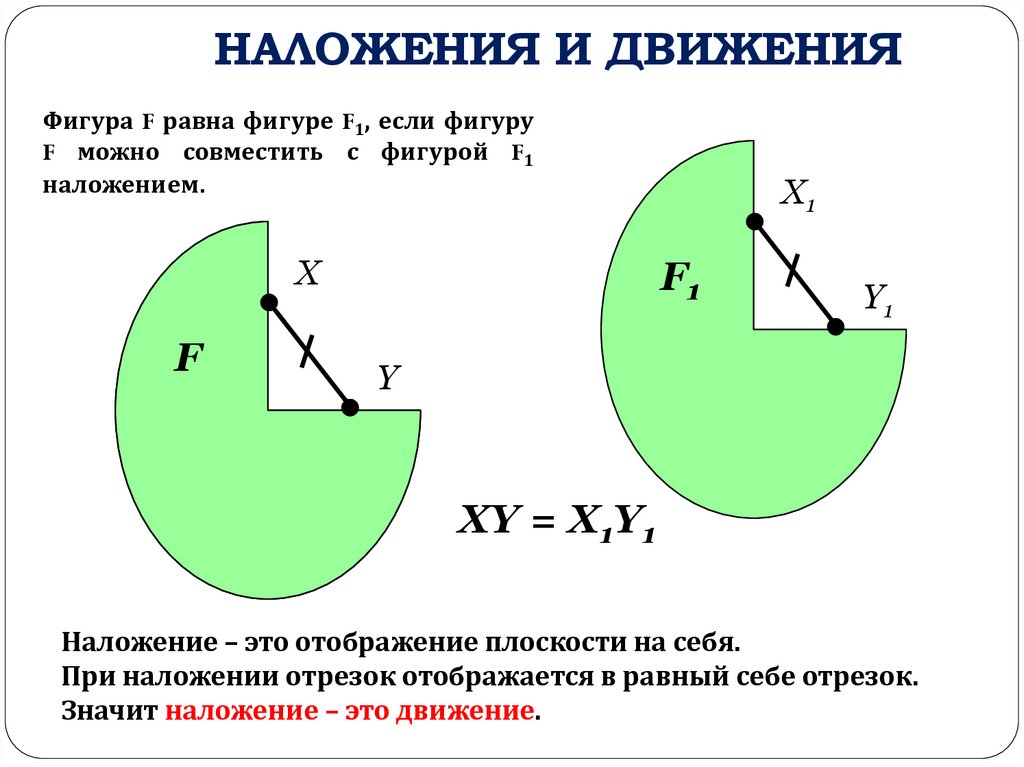
НАЛОЖЕНИЯ И ДВИЖЕНИЯФигура F равна фигуре F1, если фигуру
F можно совместить с фигурой F1
наложением.
X
FF
X1
F1
Y1
Y
XY = X1Y1
Наложение – это отображение плоскости на себя.
При наложении отрезок отображается в равный себе отрезок.
Значит наложение – это движение.
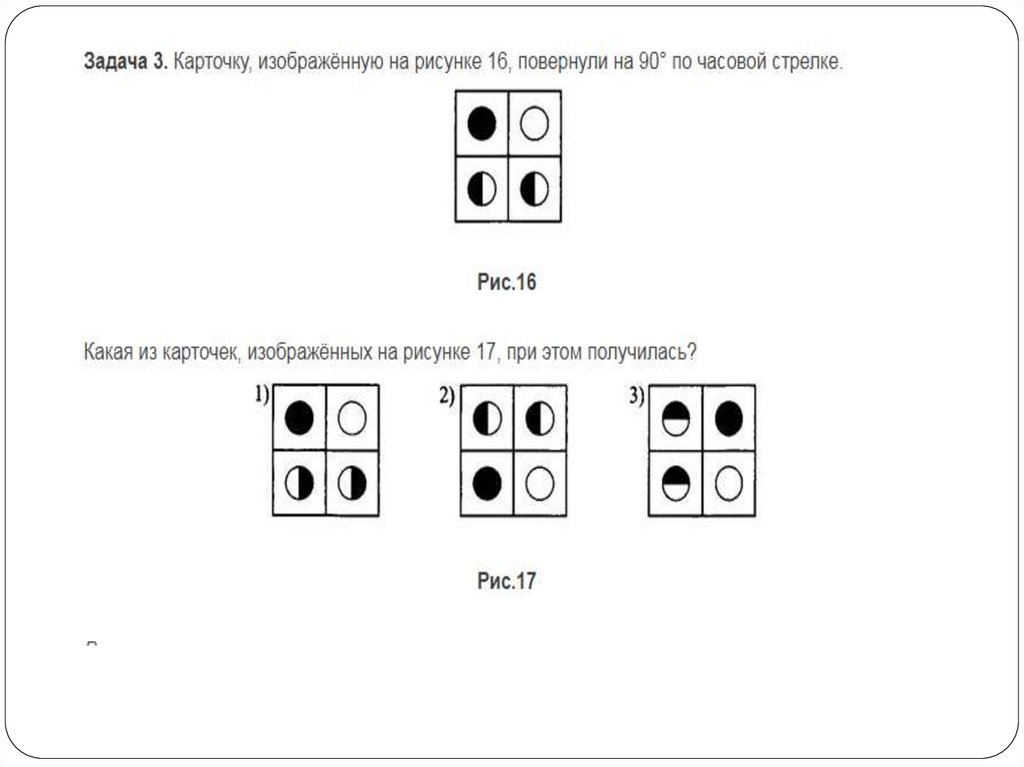
18.
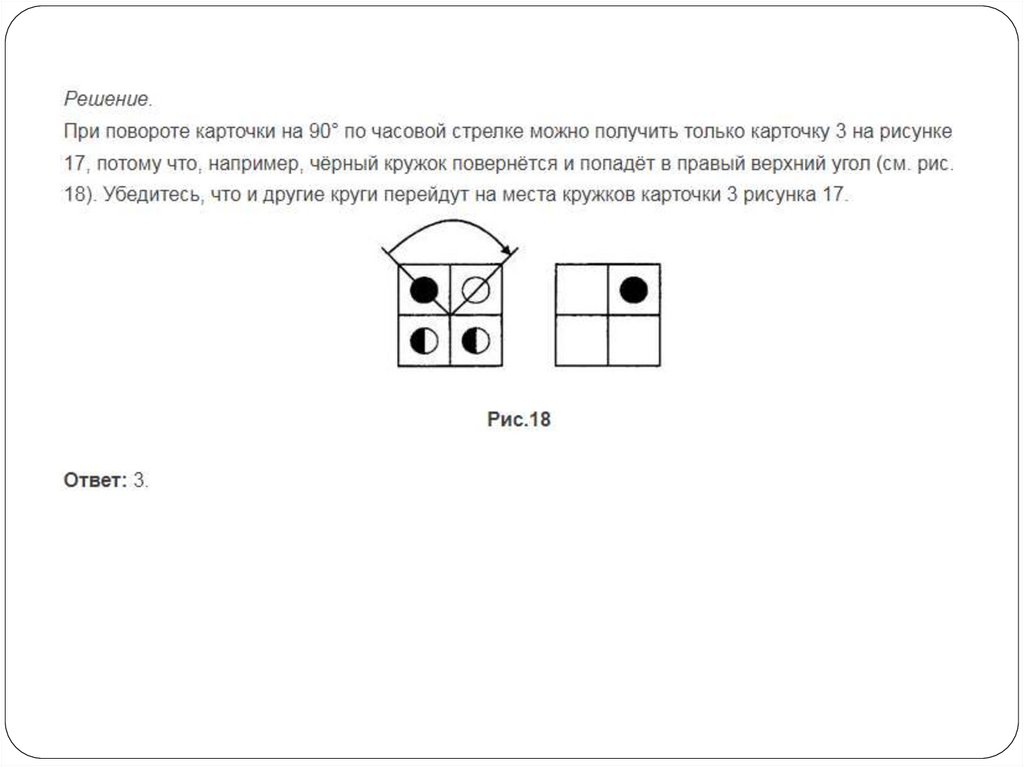
19.
20.
21.
22.
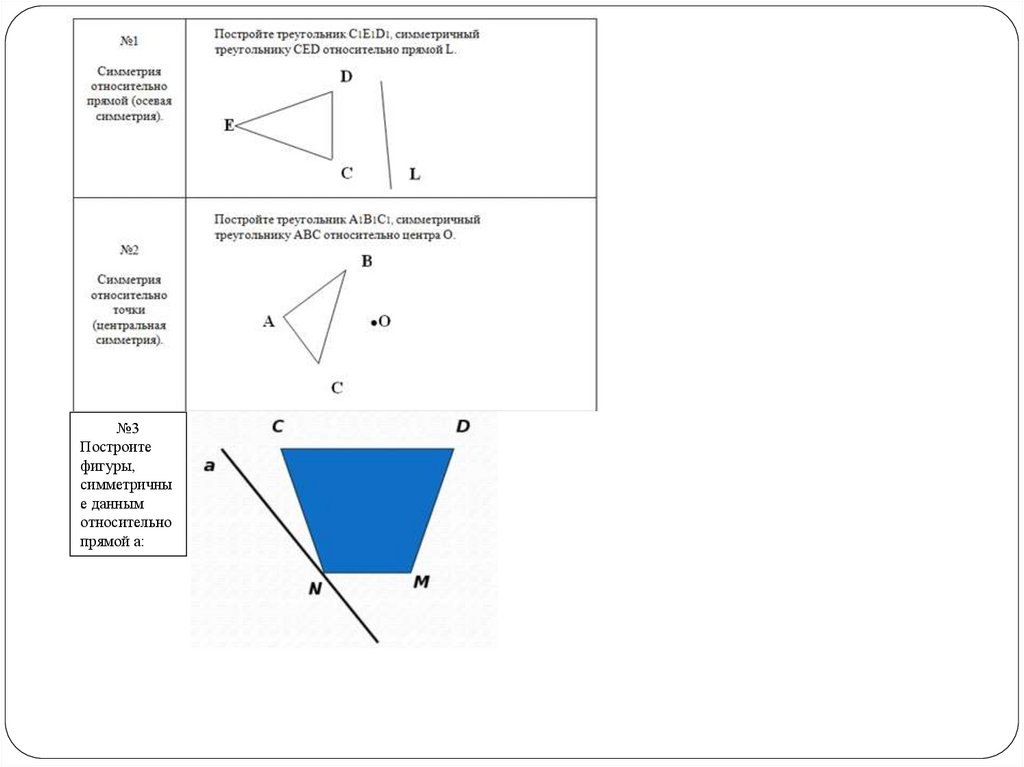
№3Построите
фигуры,
симметричны
е данным
относительно
прямой а:



 mathematics
mathematics








