Similar presentations:
Понятие движения. Осевая симметрия
1. Понятие движения
2. Цели урока:
соответствия:КаждойНайдите
т очке плоскост
и ст авит ся в
соот вет ст вие какая-т о т очка эт ой же
плоскост и, причем любая т очка плоскост и
оказывает ся сопост авленной некот орой т очке.
Говорят , чт о дано от ображение
плоскост и на себя.
(Осевая и цент ральная симмет рии)
От ображение плоскост и на себя,
сохраняющее расст ояние, называют движением
3. Найдите соответствия:
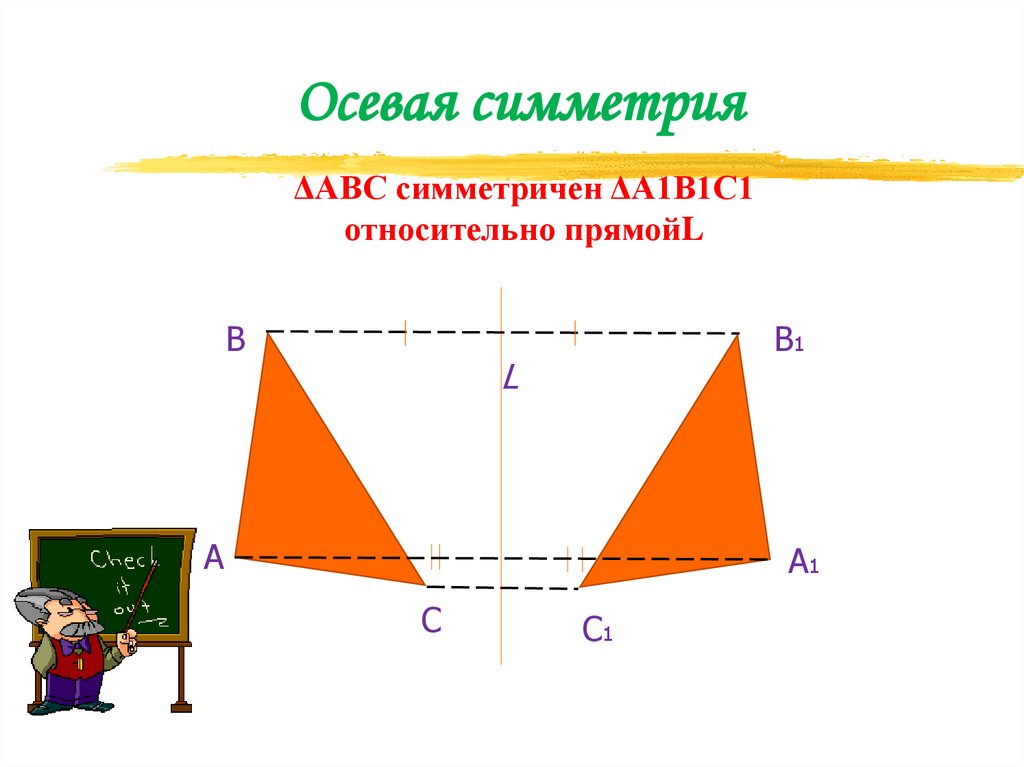
Осевая симметрияΔАВС симметричен ΔА1В1С1
относительно прямойL
В
В1
L
А
А1
С
С1
4.
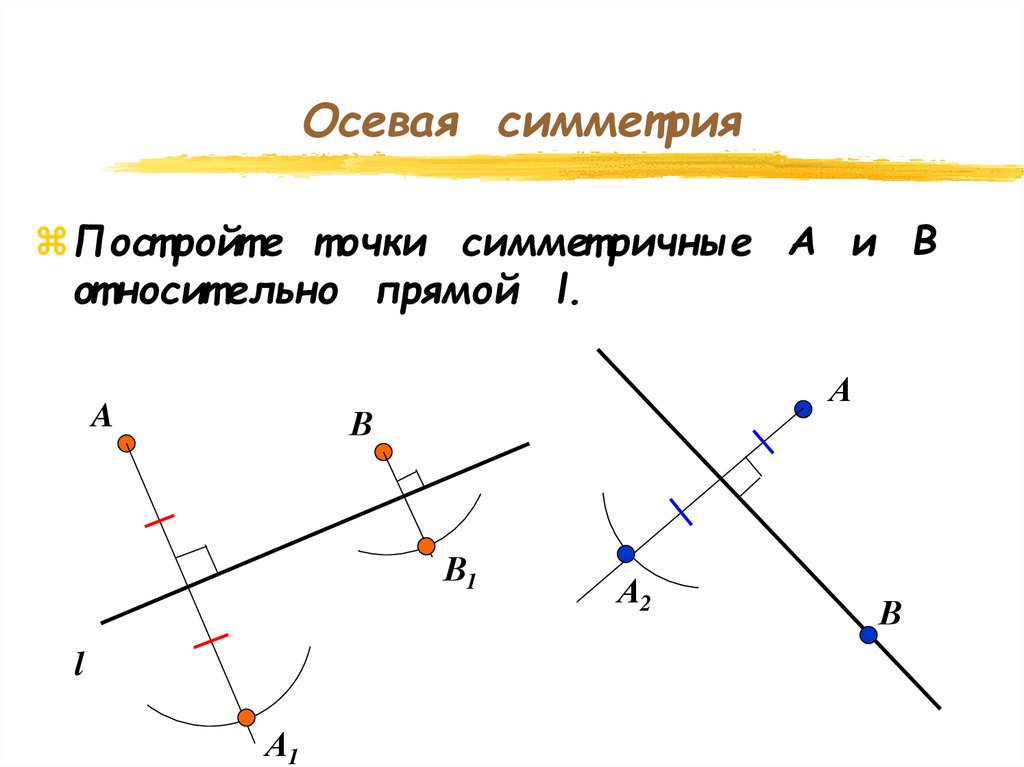
Осевая симметрияПост ройт е т очки симмет ричные А и В
от носит ельно прямой l.
A
А
В
В1
l
А1
А2
В
5. Осевая симметрия
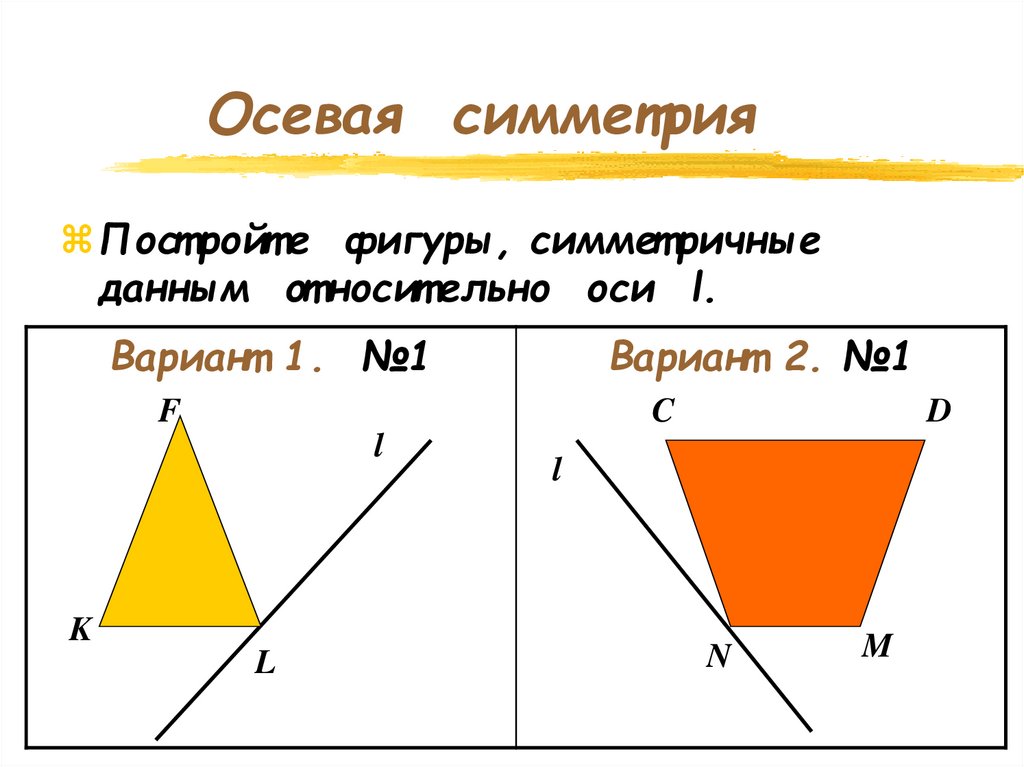
Пост ройт е фигуры, симмет ричныеданным от носит ельно оси l.
Вариант 1. №1
Вариант 2. №1
F
C
l
K
L
D
l
N
M
6. Осевая симметрия
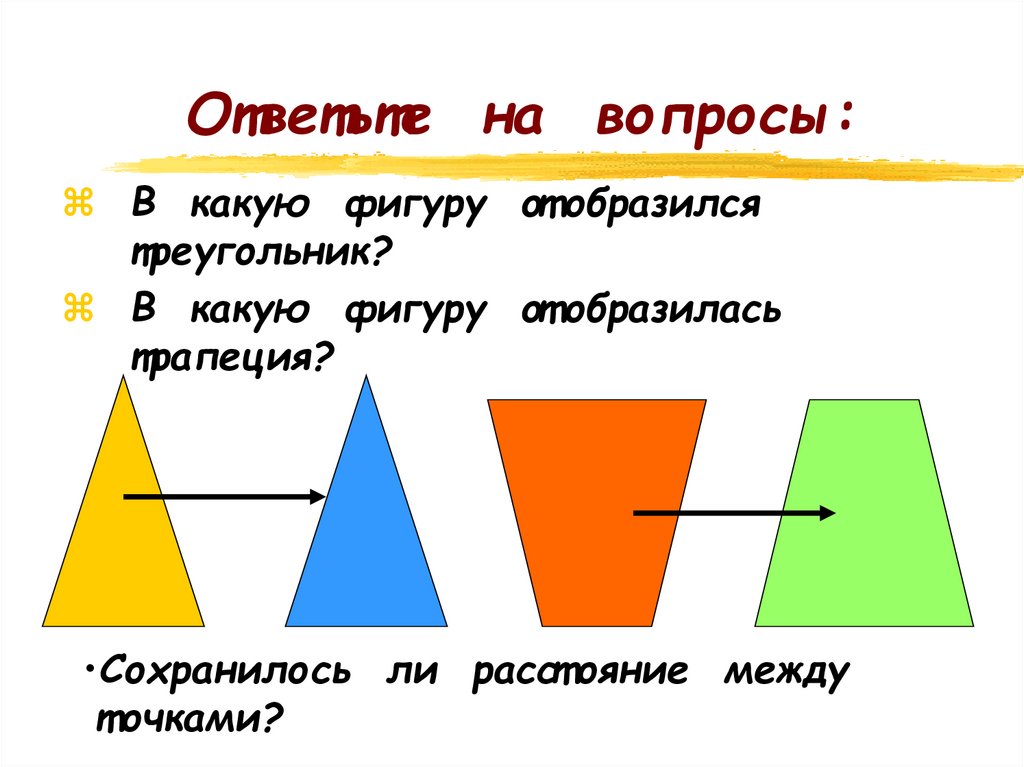
Ответьте на вопросы:В какую фигуру от образился
треугольник?
В какую фигуру от образилась
трапеция?
•Сохранилось ли расст ояние между
т очками?
7. Ответьте на вопросы:
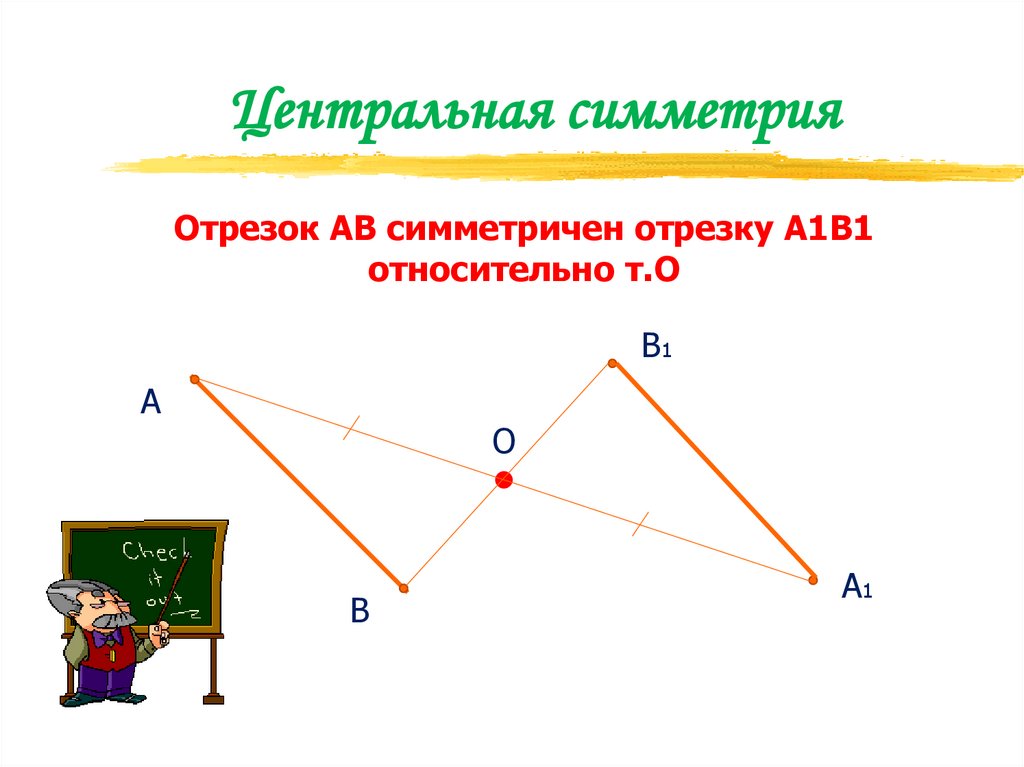
Центральная симметрияОтрезок АВ симметричен отрезку А1В1
относительно т.О
В1
А
О
В
А1
8.
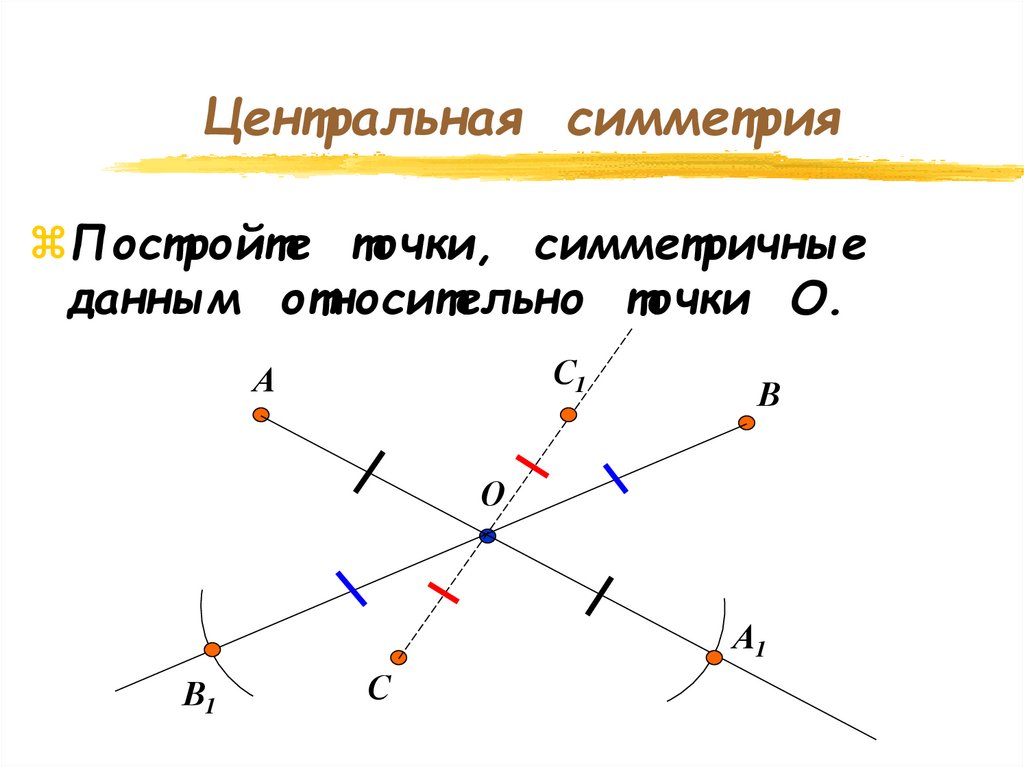
Центральная симметрияПостройте точки, симметричные
данным относительно точки О.
С1
А
В
О
А1
В1
С
9. Центральная симметрия
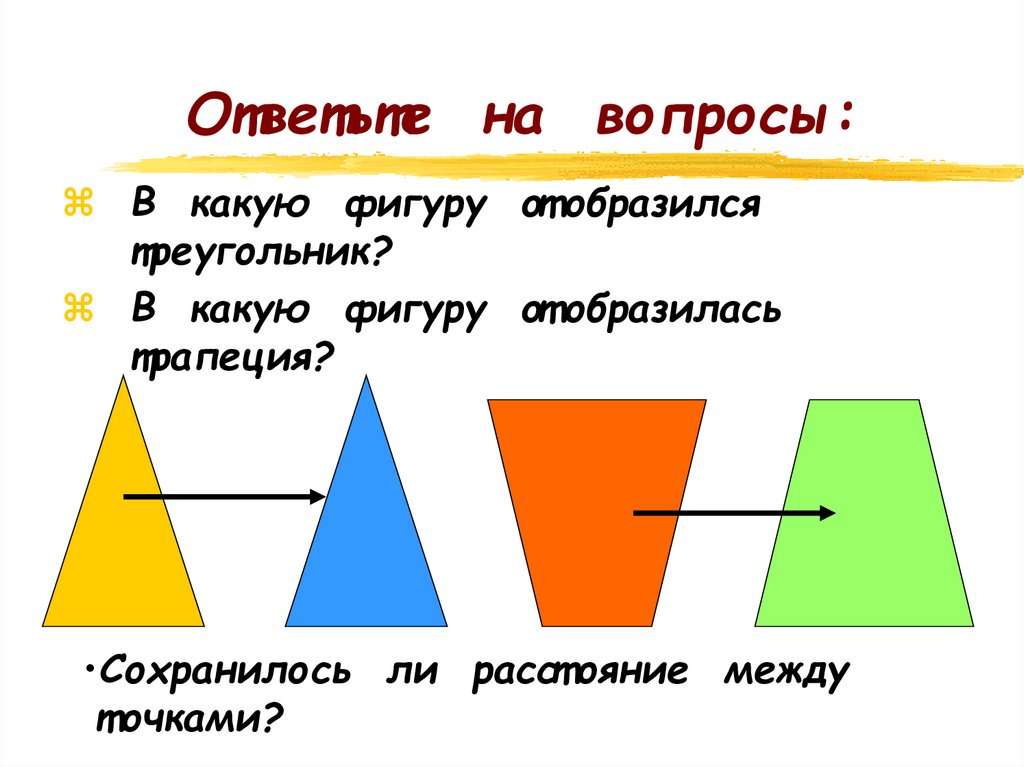
Ответьте на вопросы:В какую фигуру от образился
треугольник?
В какую фигуру от образилась
трапеция?
•Сохранилось ли расст ояние между
т очками?
10. Ответьте на вопросы:
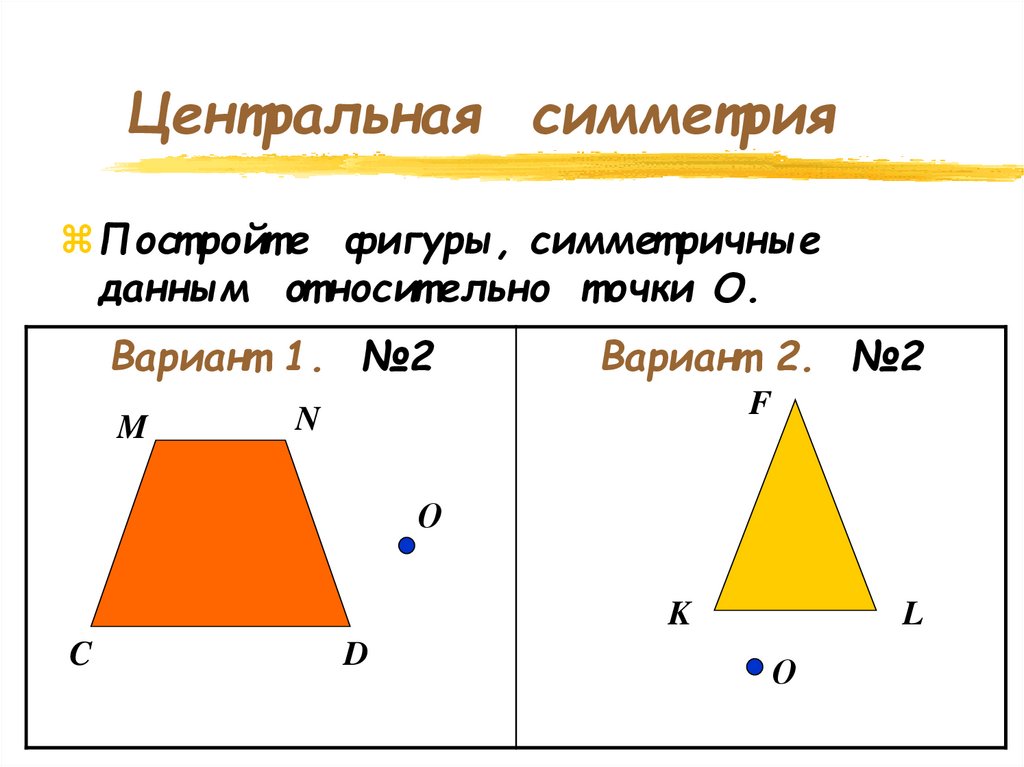
Центральная симметрияПост ройт е фигуры, симмет ричные
данным от носит ельно т очки О.
Вариант 1. №2
M
Вариант 2. №2
F
N
О
K
C
D
L
О
11. Центральная симметрия
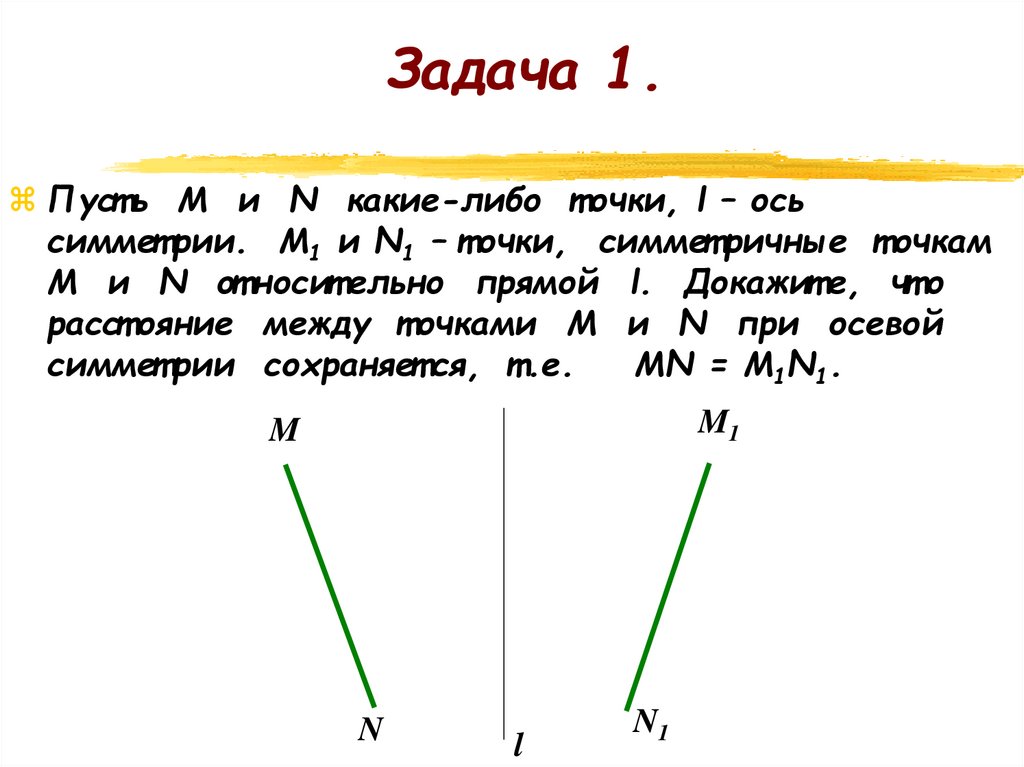
Задача 1.Пуст ь М и N какие-либо т очки, l – ось
симмет рии. М1 и N1 – т очки, симмет ричные т очкам
М и N от носит ельно прямой l. Докажит е, чт о
расст ояние между т очками М и N при осевой
симмет рии сохраняет ся, т .е.
МN = M1N1.
M1
M
N
l
N1
12. Задача 1.
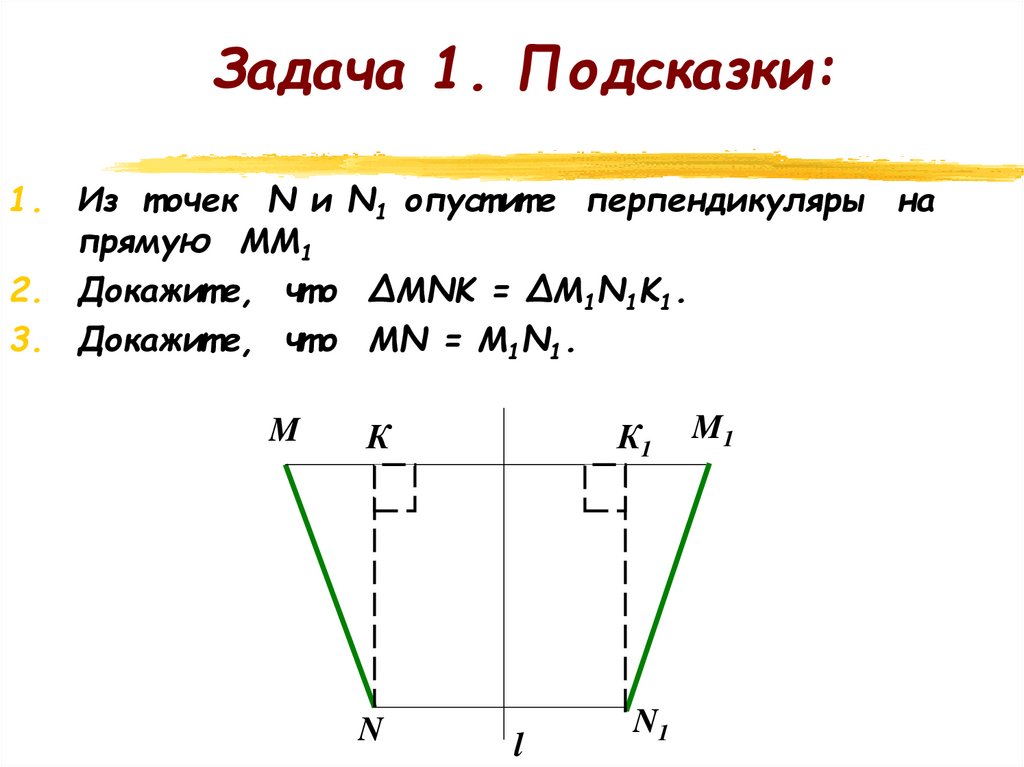
Подсказки:1. Из т очек N и N1 опуст ит е перпендикуляры на
прямую ММ1
2. Докажит е, чт о ∆MNK = ∆M1N1K1.
3. Докажит е, чт о МN = М1N1.
M
К
К1
N
N1
l
M1
13. Задача 1. Подсказки:
Понятие движенияПусть каждой точке плоскости ставится в
соответствие какая-то точка этой же плоскости,
причем любая точка плоскости оказывается
сопоставленной некоторой точке. Тогда
говорят, что дано отображение плоскости на
себя.
Осевая симметрия и центральная
симметрия есть отображение плоскости
на себя.
14.
Понятие движенияДвижение плоскости – это
отображение плоскости на
себя, сохраняющее
расстояние.
15.
Задача 2. (№3)Докажит е, чт о цент ральная симмет рия
ест ь движение.
Подсказки:
1)
2)
3)
4)
Возьмит е т очки М и N и О – цент р симмет рии.
Пост ройт е т очки М1 и N1 от носит ельно т очки О.
Докажит е, чт о ∆ОМN = ∆OM1N1.
Докажит е, чт о МN = M1N1.
Отображение плоскости
на себя,
сохраняющее расстояние,
называют движением





 mathematics
mathematics








