Свойства биссектрис треугольника. Тематическая подготовка к ОГЭ

1. Рациональные методы решения задач. Свойства биссектрис (и не только) треугольника.

Тематическая подготовка к ОГЭ.

2. Что мы знаем о биссектрисе треугольника из школьного учебника?

3. Определение

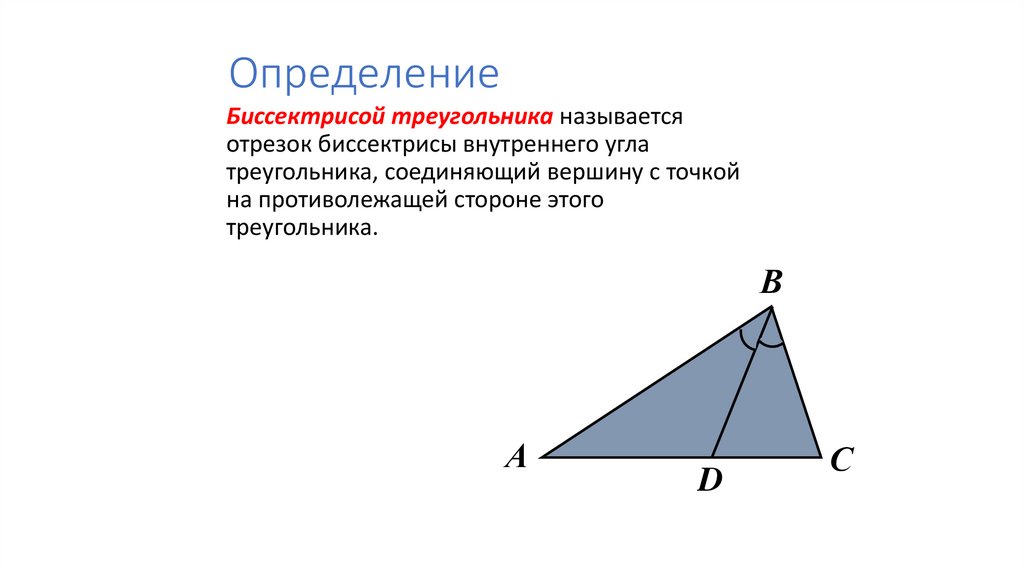
Биссектрисой треугольника называется
отрезок биссектрисы внутреннего угла
треугольника, соединяющий вершину с точкой
на противолежащей стороне этого
треугольника.
В
А
D
С

4. Свойства биссектрисы

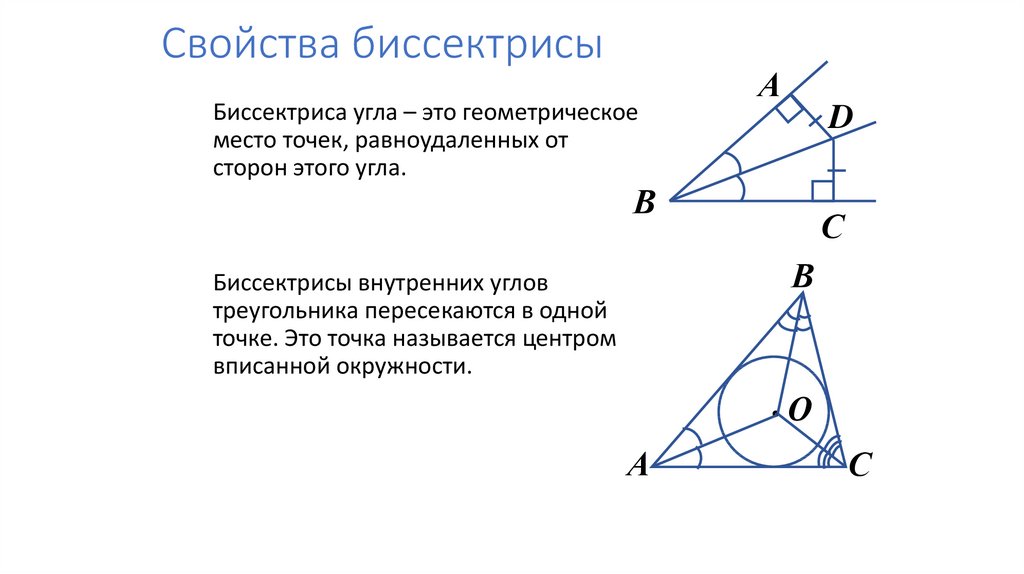
Биссектриса угла – это геометрическое
место точек, равноудаленных от
сторон этого угла.
А
D
В
С
В
Биссектрисы внутренних углов
треугольника пересекаются в одной
точке. Это точка называется центром
вписанной окружности.
О
А
С

5.

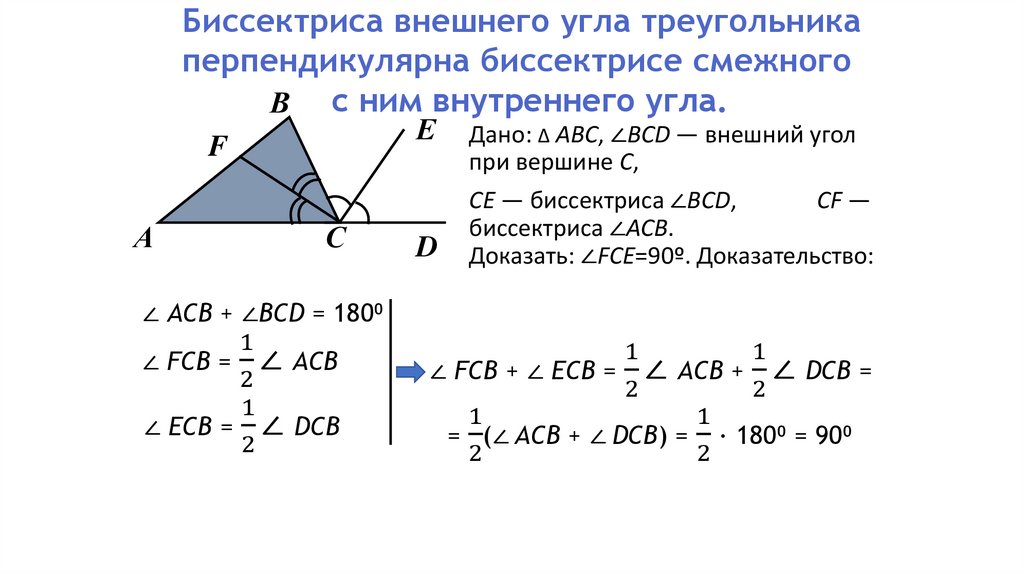
Биссектриса внешнего угла треугольника
перпендикулярна биссектрисе смежного
В с ним внутреннего угла.
Е
F
А
С
∠ ACB + ∠BCD = 180⁰
1
∠ FCB = ∠ ACB
2
1
∠ ECB = ∠ DCB
2
D
Дано: ∆ ABC, ∠BСD — внешний угол
при вершине C,
CE — биссектриса ∠BCD,
CF —
биссектриса ∠ACB.
Доказать: ∠FCE=90º. Доказательство:
1
1
∠ FCB + ∠ ECB = ∠ ACB + ∠ DCB =
2
2
1
1
= (∠ ACB + ∠ DCB) = ∙ 180⁰ = 90⁰
2
2

6.

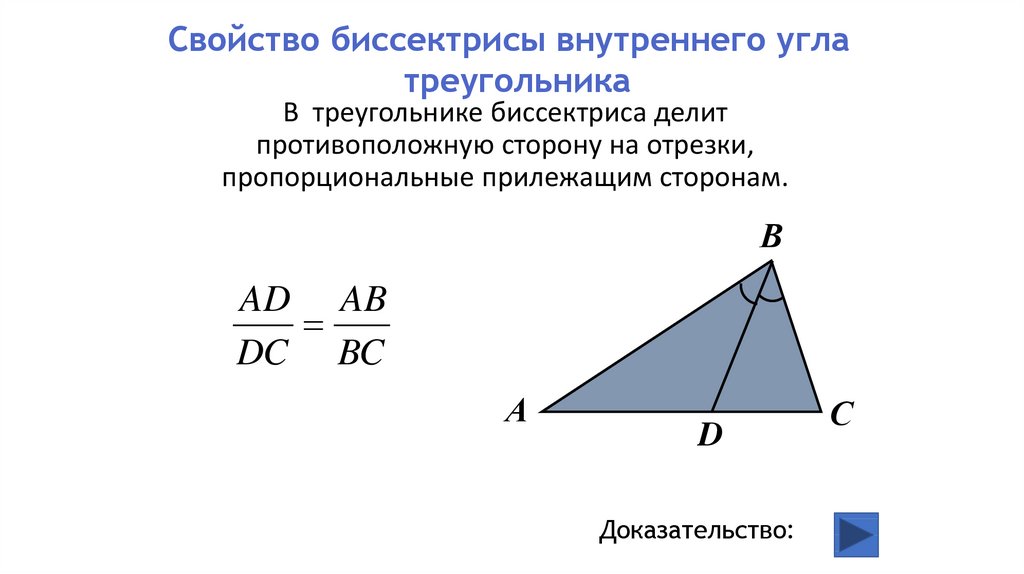
Свойство биссектрисы внутреннего угла
треугольника
В треугольнике биссектриса делит
противоположную сторону на отрезки,
пропорциональные прилежащим сторонам.
В
AD AB
DC BC
А
D
Доказательство:
С

7.

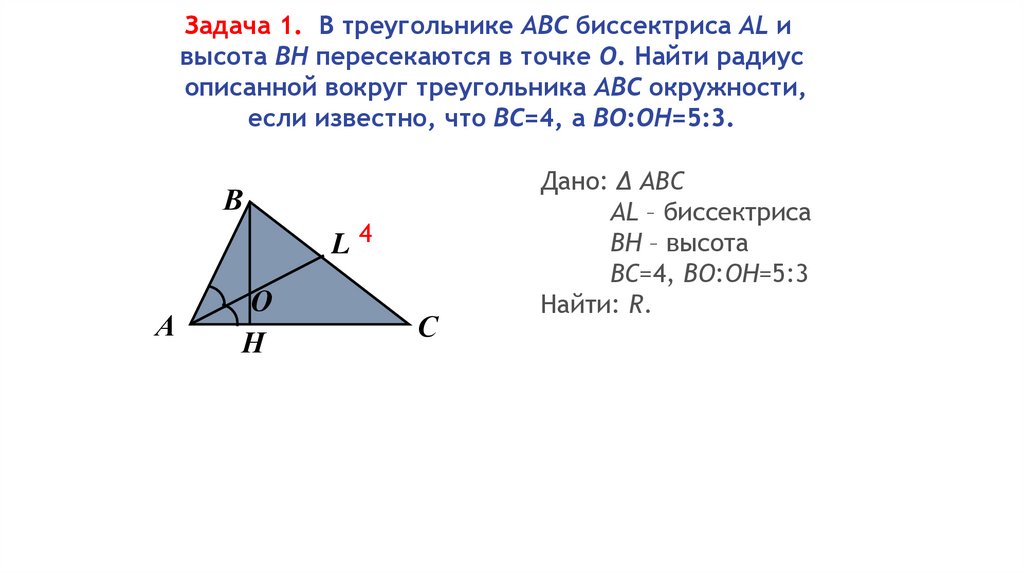
Задача 1. В треугольнике АВС биссектриса AL и
высота ВН пересекаются в точке О. Найти радиус
описанной вокруг треугольника АВС окружности,
если известно, что ВС=4, а ВО:ОН=5:3.
В
L4
А
О
Н
С
Дано: ∆ АВС
AL – биссектриса
ВН – высота
ВС=4, BО:ОН=5:3
Найти: R.

8.

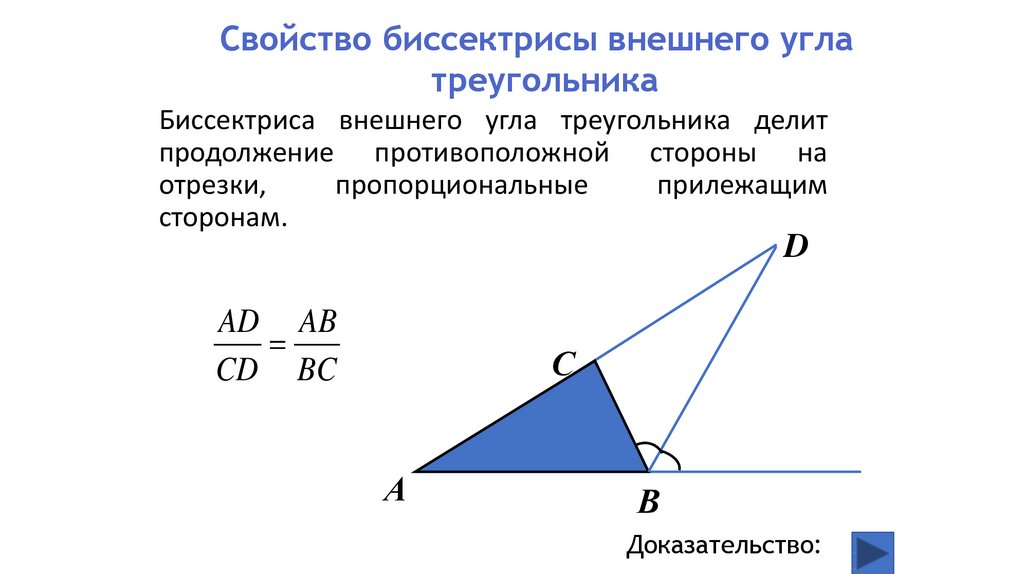
Свойство биссектрисы внешнего угла
треугольника
Биссектриса внешнего угла треугольника делит
продолжение противоположной стороны на
отрезки,
пропорциональные
прилежащим
сторонам.
D
AD AB
CD BC
С
А
В
Доказательство:

9.

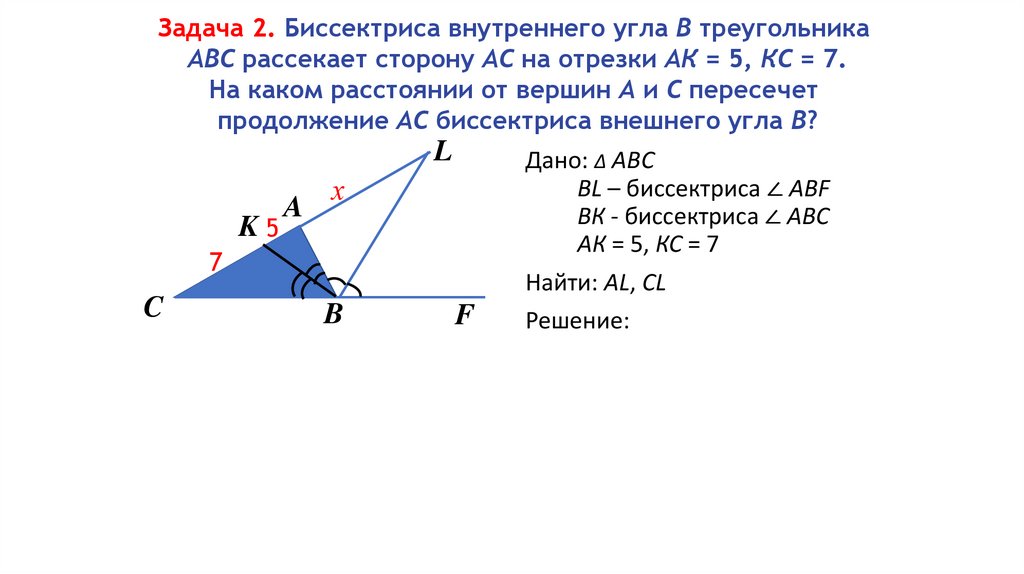
Задача 2. Биссектриса внутреннего угла В треугольника
АВС рассекает сторону АС на отрезки АК = 5, КС = 7.
На каком расстоянии от вершин А и С пересечет
продолжение АС биссектриса внешнего угла В?
L
K5
A
х
7
C
B
F
Дано: ∆ АВС
BL – биссектриса ∠ АBF
ВК - биссектриса ∠ АBС
АК = 5, КС = 7
Найти: AL, CL
Решение:

10.

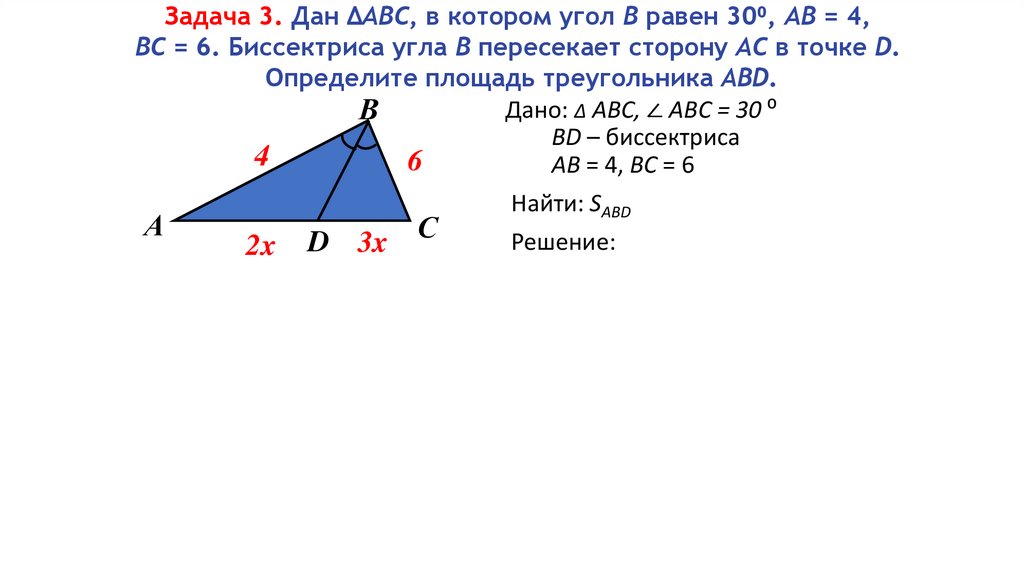
Задача 3. Дан ΔАВС, в котором угол В равен 30⁰, АВ = 4,
ВС = 6. Биссектриса угла В пересекает сторону АС в точке D.
Определите площадь треугольника ABD.
Дано: ∆ АВС, ∠ ABC = 30 ⁰
В
BD – биссектриса
4
6
АB = 4, BС = 6
Найти: SABD
А
С
Решение:
2x D 3x

11.

Биссектриса угла треугольника делит его
площадь на части, пропорциональные
прилежащим сторонам.
В
Дано: Δ ABC; BD – биссектриса
Доказать: SABD : SBDC = AB:BC
Доказательство:
А
D
H
С
1. ΔABD и ΔDBC имеют общую высоту BH,
SABD : SBDC = AD:DC.
2. BD – биссектриса
3. SABD : SBDC =AD:DC
AD:DC = AB:BC
AD:DC = AB:BC.
SABD : SBDC = AB:BC

12.

Решение задачи 3 с использованием свойства биссектрисы.
Дан ΔАВС, в котором
угол В равен 30⁰, АВ = 4, ВС = 6. Биссектриса
Дано: ∆ АВС, ∠ ABC = 30 ⁰
угла В пересекает сторону АС в точке D.
BD – биссектриса
Определите площадь треугольника ABD.
АB = 4, BС = 6
В
4
А
Найти: SABD
Решение:
6
D
С

13.

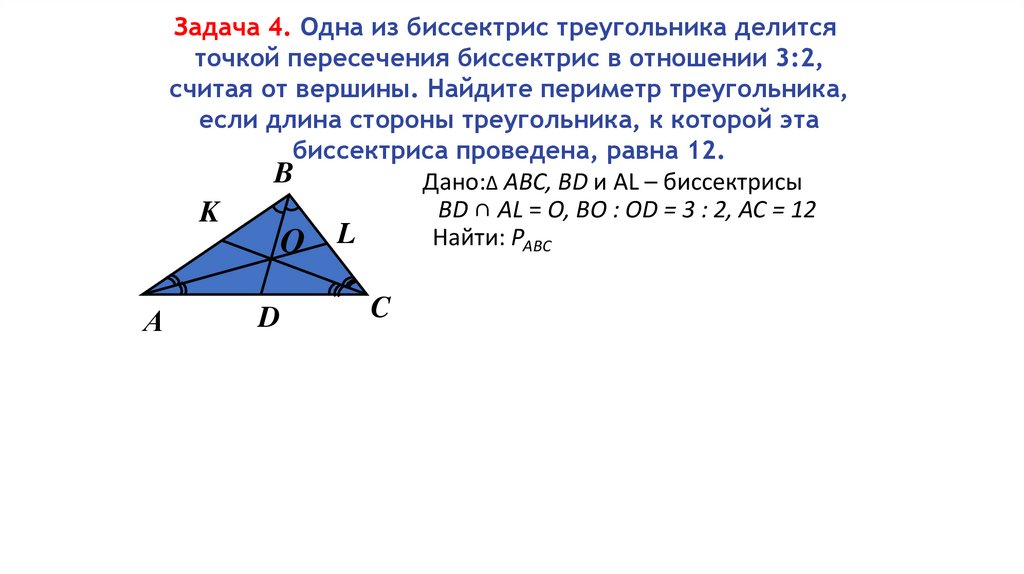
Задача 4. Одна из биссектрис треугольника делится
точкой пересечения биссектрис в отношении 3:2,
считая от вершины. Найдите периметр треугольника,
если длина стороны треугольника, к которой эта
биссектриса проведена, равна 12.
B
Дано:Δ АВС, BD и AL – биссектрисы
BD ∩ AL = O, BО : OD = 3 : 2, АС = 12
K
Найти: РАВС
O L
А
D
C