Similar presentations:
Свойства равнобедренного треугольника
1. Свойства равнобедренного треугольника
17.11.20212. Равнобедренный треугольник
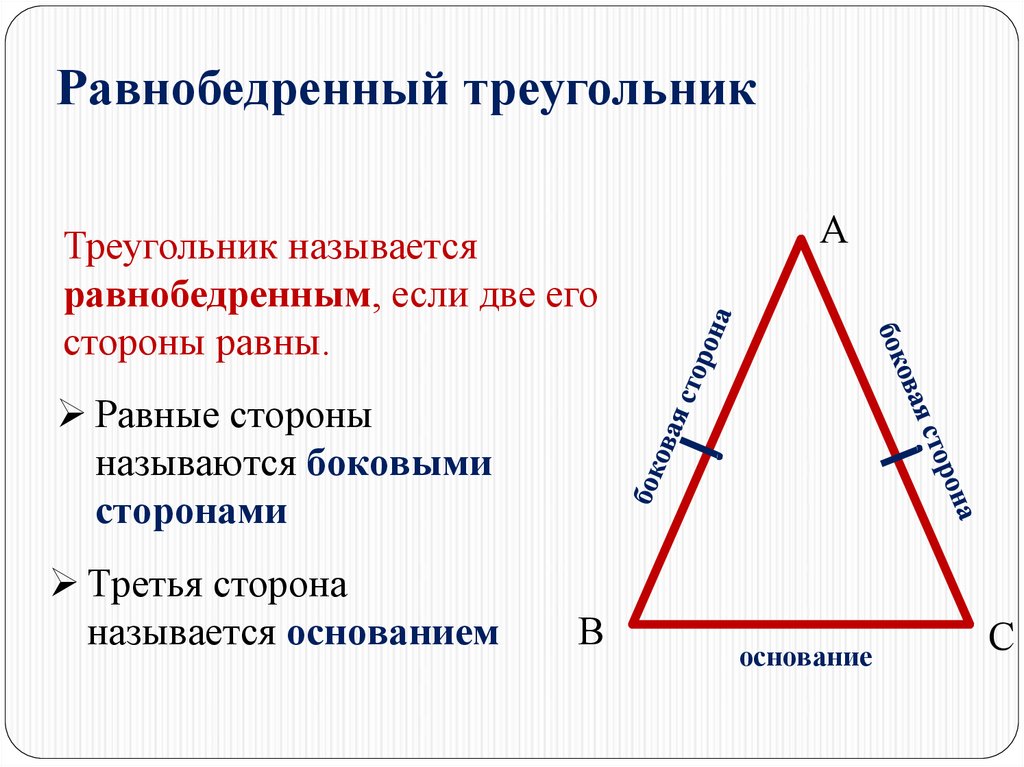
Треугольник называетсяравнобедренным, если две его
стороны равны.
А
Равные стороны
называются боковыми
сторонами
Третья сторона
называется основанием
В
основание
С
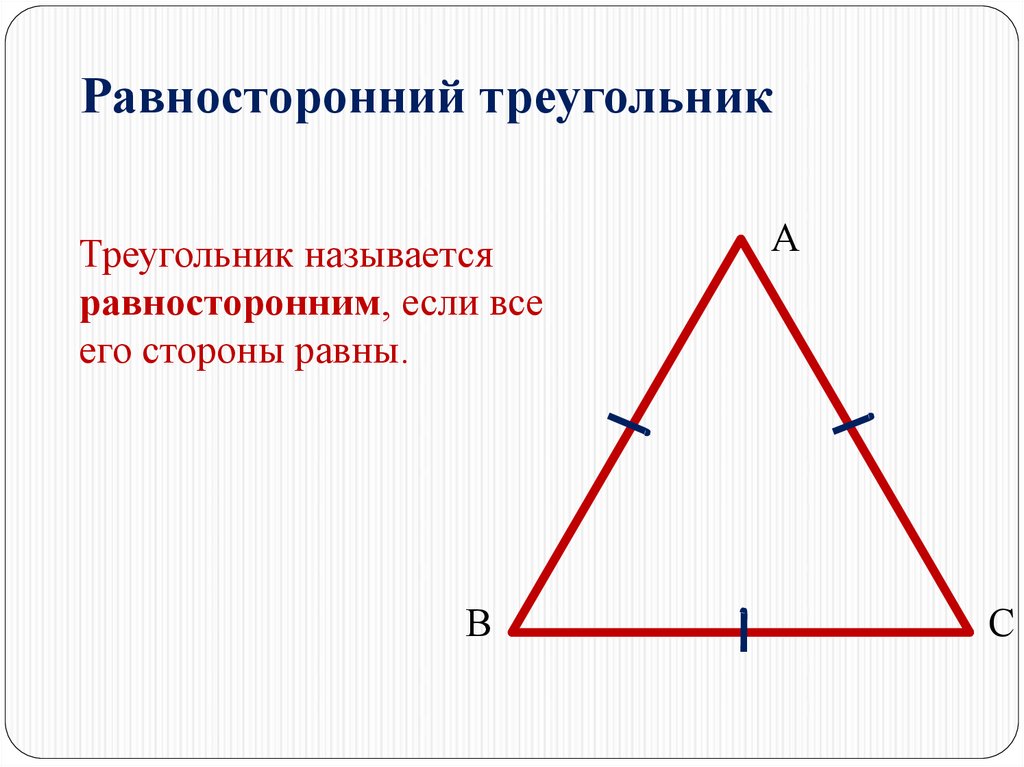
3. Равносторонний треугольник
Треугольник называетсяравносторонним, если все
его стороны равны.
В
А
С
4. В равнобедренном треугольнике углы при основании равны
Дано:А
АВС - равнобедренный
BC - основание
Доказать: B C
1 2
В
D
С
Доказательство:
AD- биссектриса АВС
АВD ADC
по первому признаку (т.к.
AB=AC - по условию, ADобщая сторона, 1 2 )
В равных треугольниках против равных сторон лежат
равные углы , поэтому B C
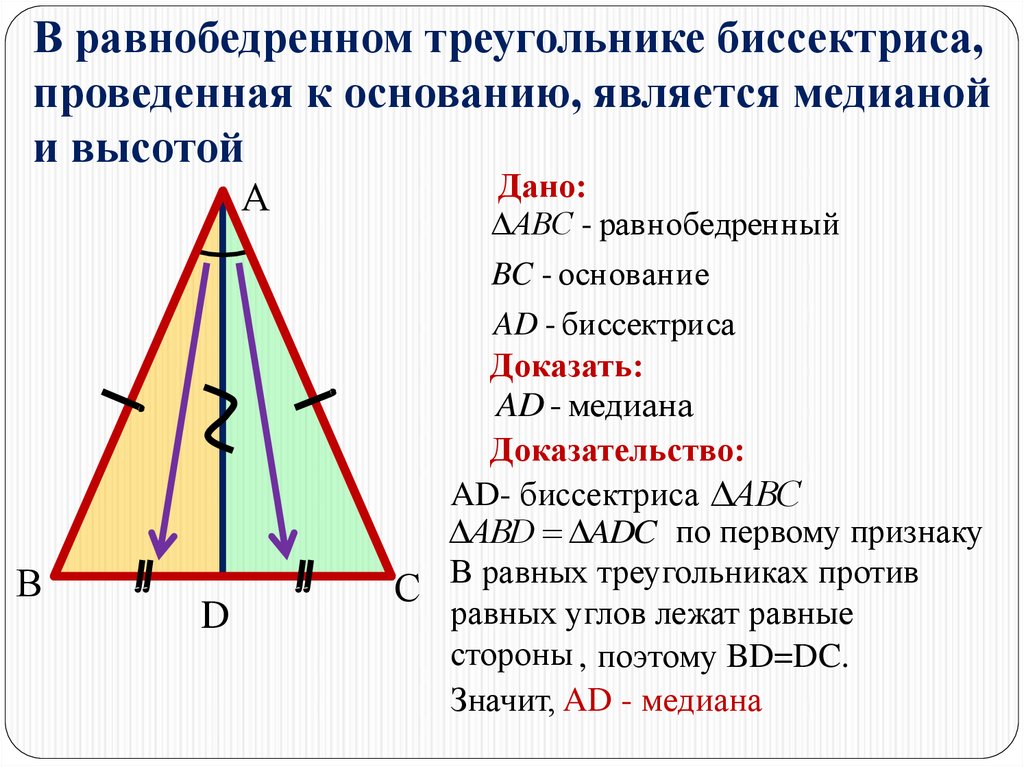
5. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
АВ
D
Дано:
АВС - равнобедренный
BC - основание
AD - биссектриса
Доказать:
AD - медиана
Доказательство:
AD- биссектриса АВС
АВD ADC по первому признаку
С В равных треугольниках против
равных углов лежат равные
стороны , поэтому BD=DC.
Значит, AD - медиана
6. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
Дано:АВС - равнобедренный
BC - основание
AD - биссектриса
Доказать:
AD - высота
Доказательство:
AD- биссектриса АВС
АВD ADC по первому признаку
В
С В равных треугольниках против
равных сторон лежат равные углы,
D
поэтому BDA CDA
BDA и CDA - смежные, BDA CDA 180 , BDA CDA 90 .
Значит, AD – высота.
А
7.
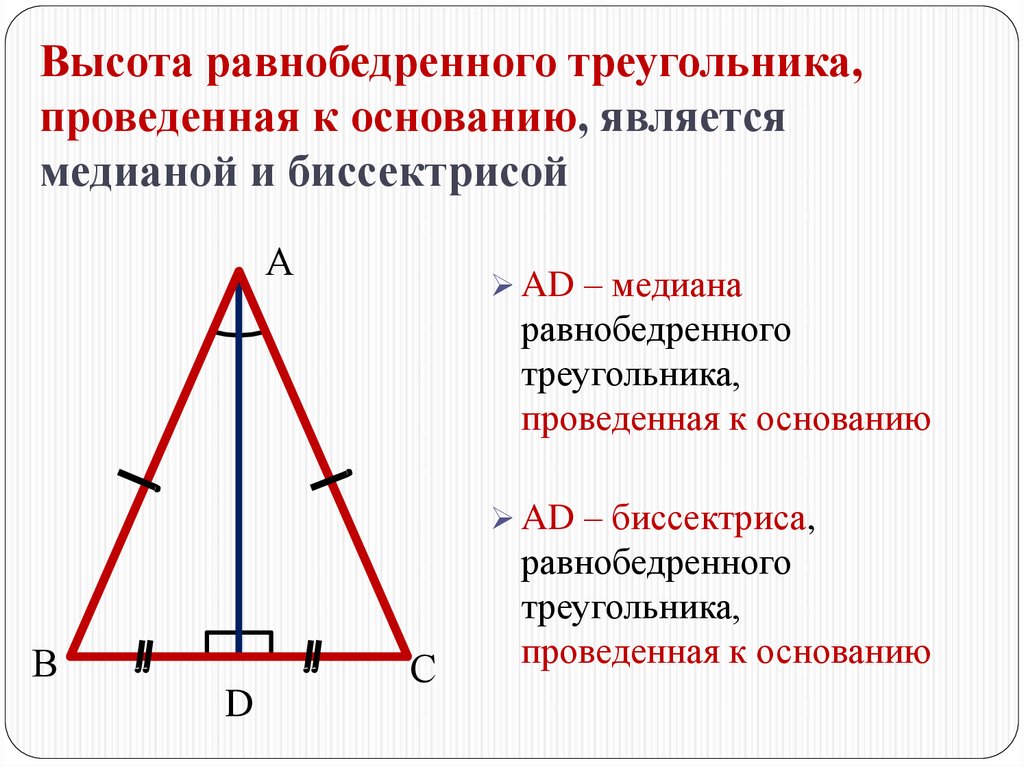
Высота равнобедренного треугольника,проведенная к основанию, является
медианой и биссектрисой
А
AD – медиана
равнобедренного
треугольника,
проведенная к основанию
AD – биссектриса,
В
D
С
равнобедренного
треугольника,
проведенная к основанию
8.
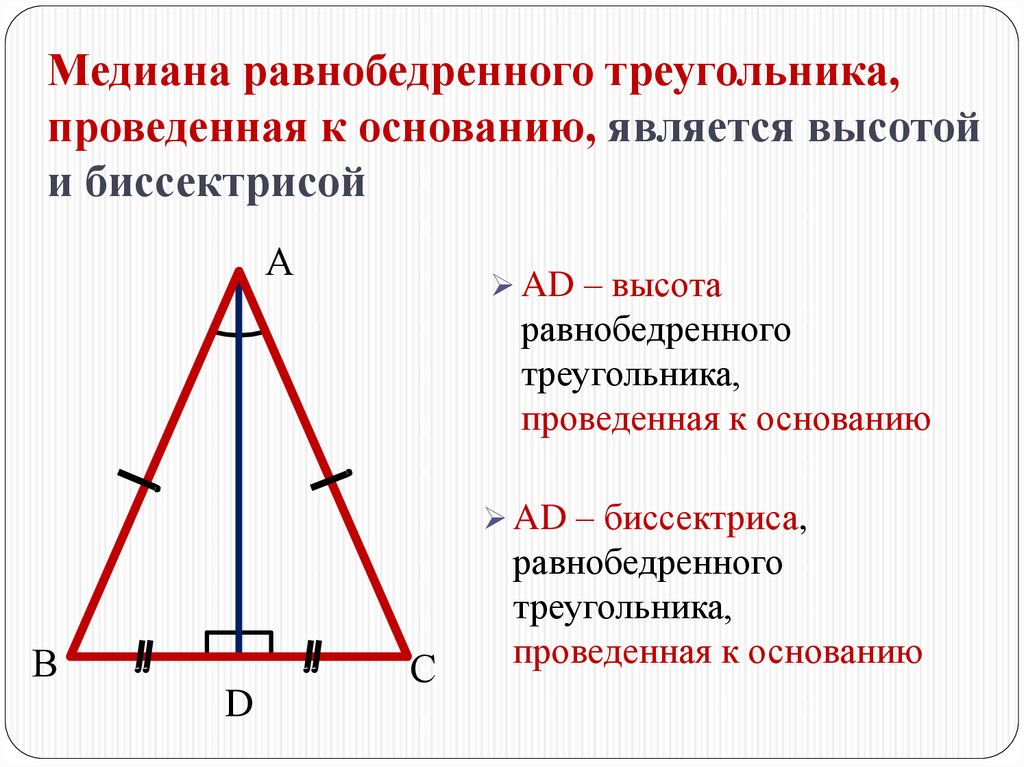
Медиана равнобедренного треугольника,проведенная к основанию, является высотой
и биссектрисой
А
AD – высота
равнобедренного
треугольника,
проведенная к основанию
AD – биссектриса,
В
D
С
равнобедренного
треугольника,
проведенная к основанию
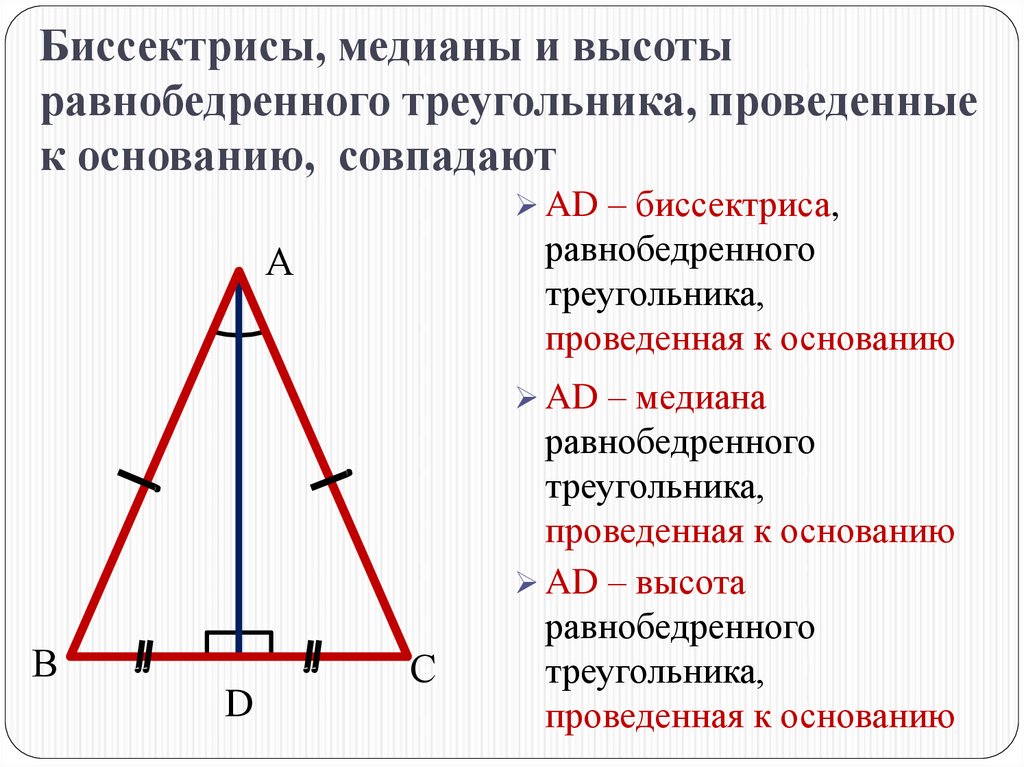
9. Биссектрисы, медианы и высоты равнобедренного треугольника, проведенные к основанию, совпадают
AD – биссектриса,равнобедренного
треугольника,
проведенная к основанию
А
AD – медиана
В
D
С
равнобедренного
треугольника,
проведенная к основанию
AD – высота
равнобедренного
треугольника,
проведенная к основанию
10.
11.
D70°
А
С
70°
Проверь себя!
12.
А65°
С
D
115°
В
Проверь себя!
13.
С40°
А
В
D
40°
Проверь себя!
14.
ВА
С
D
65°
К
65°
Проверь себя!
15.
АD
С
30°
В
60°
Проверь себя!
16.
МК
D
40°
С
80°
В
А
Проверь себя!
17.
КD
А
40°
С
100°
В
Проверь себя!
18.
ВА
С
90°
D
Проверь себя!
19.
ЕВ
70°
С
D
55°
А
Проверь себя!
20.
А50°
D
В
Е
25°
С
Проверь себя!
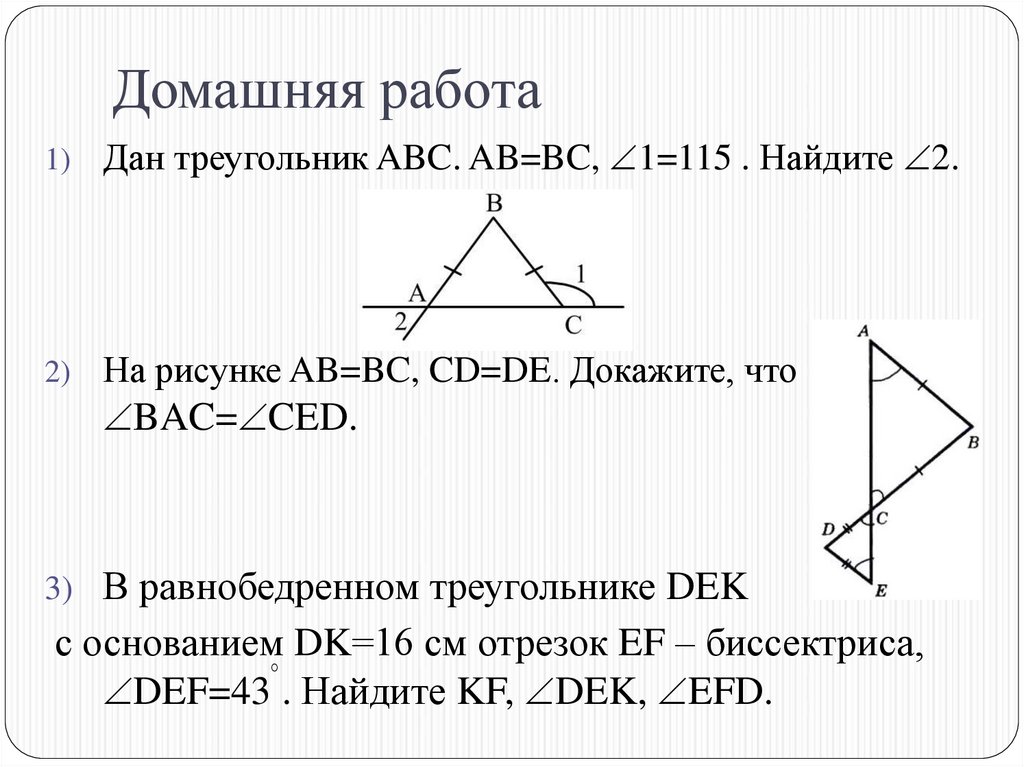
21. Домашняя работа
1)Дан треугольник ABC. AB=BC, 1=115 . Найдите 2.
2)
На рисунке AB=BC, CD=DE. Докажите, что
BAC= CED.
3) В равнобедренном треугольнике DEK
с основанием DK=16 см отрезок EF – биссектриса,
DEF=43 . Найдите KF, DEK, EFD.














 mathematics
mathematics