Равнобедренный треугольник и его свойства

1.

1

2.

На каких рисунках изображены:
а) медианы:
2

3.

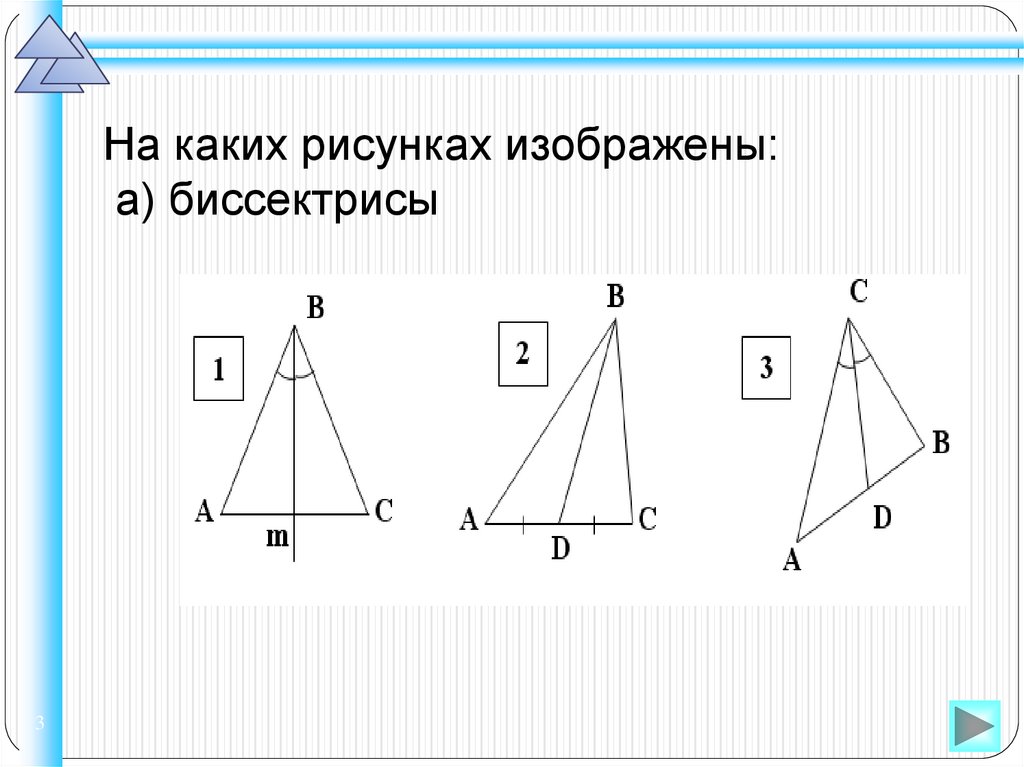
На каких рисунках изображены:
а) биссектрисы
3

4.

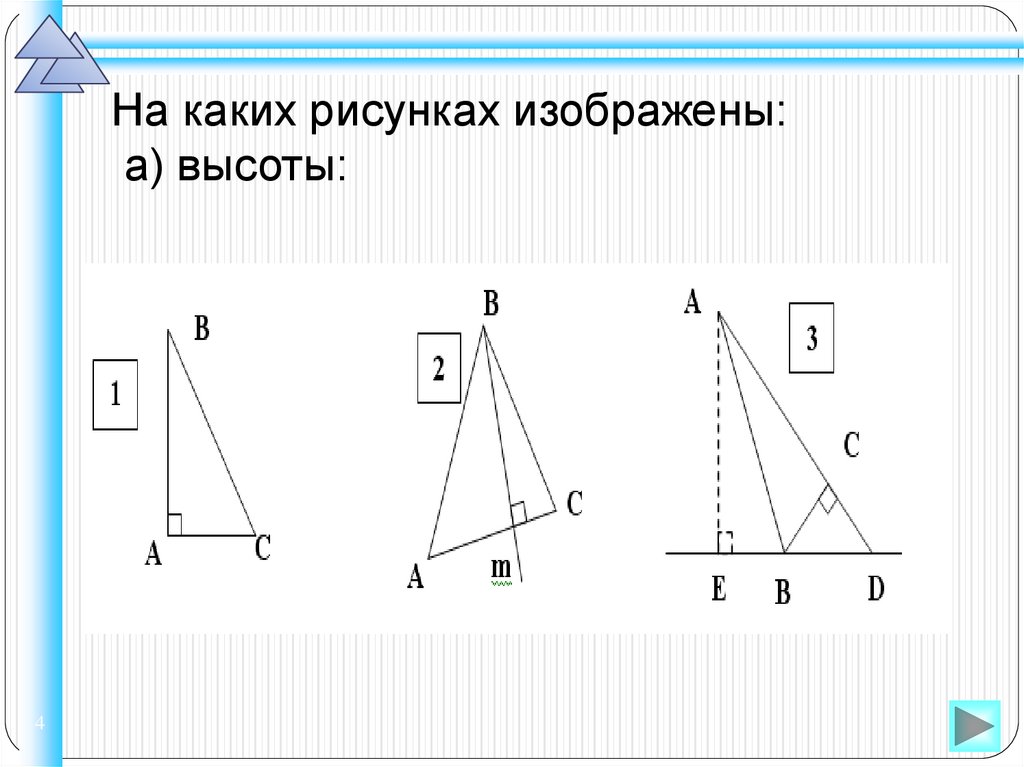
На каких рисунках изображены:
а) высоты:
4

5.

Классификация треугольников по
?
углам
-остроугольный
-тупоугольный
-прямоугольный
5
сторонам
?
-равнобедренный
-равносторонний
-разносторонний

6.

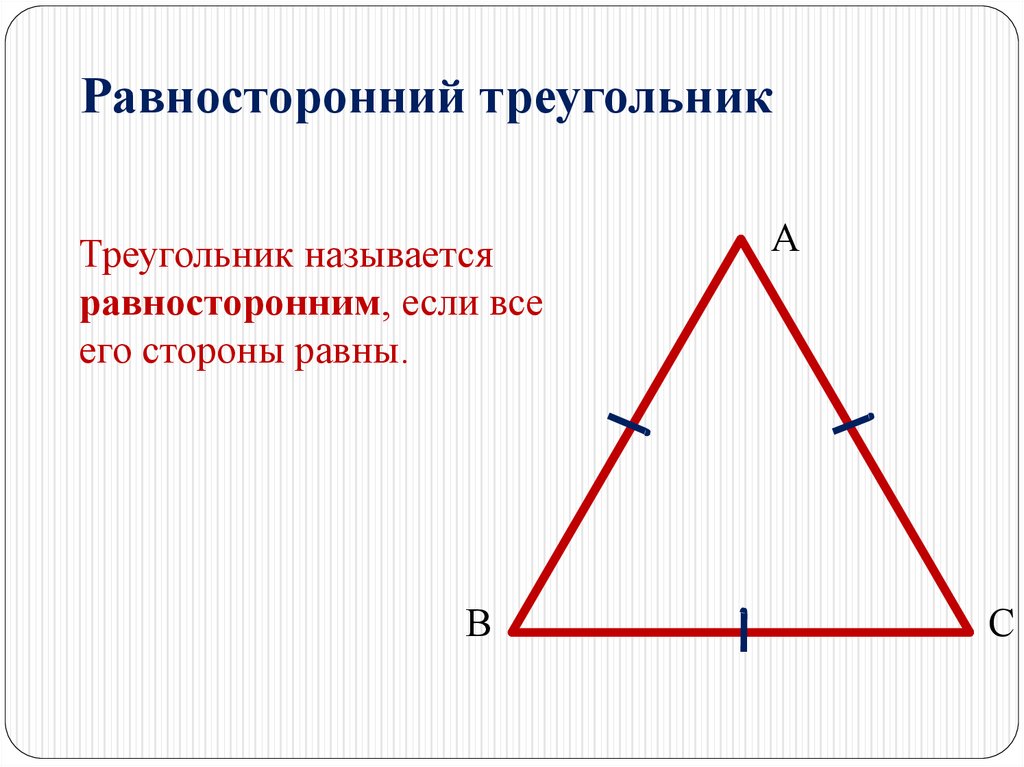
Равносторонний треугольник
Треугольник называется
равносторонним, если все
его стороны равны.
В
А
С

7.

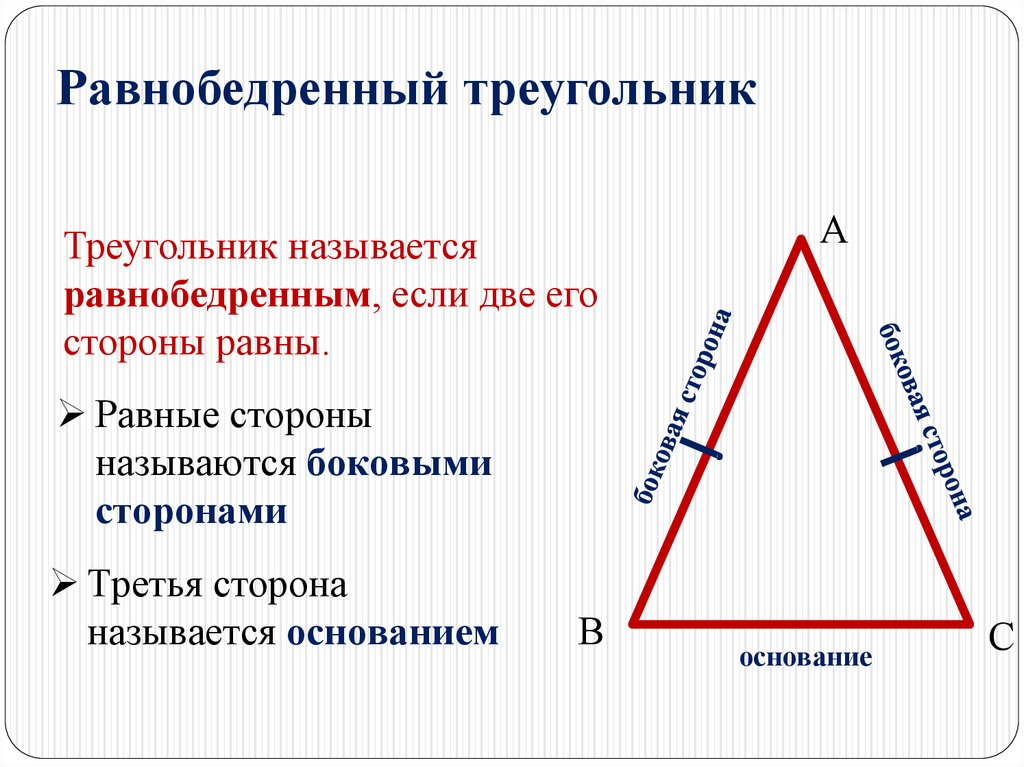
Равнобедренный треугольник
Треугольник называется
равнобедренным, если две его
стороны равны.
А
Равные стороны
называются боковыми
сторонами
Третья сторона
называется основанием
В
основание
С

8.

В равнобедренном треугольнике углы при
основании равны
А
Дано:
АВС - равнобедренный
BC - основание
Доказать: B C
Доказательство:
AD- биссектриса АВС
В
АВD ADC
С
по первому признаку
В равных треугольниках против равных сторон лежат
равные углы , поэтому B C
D

9.

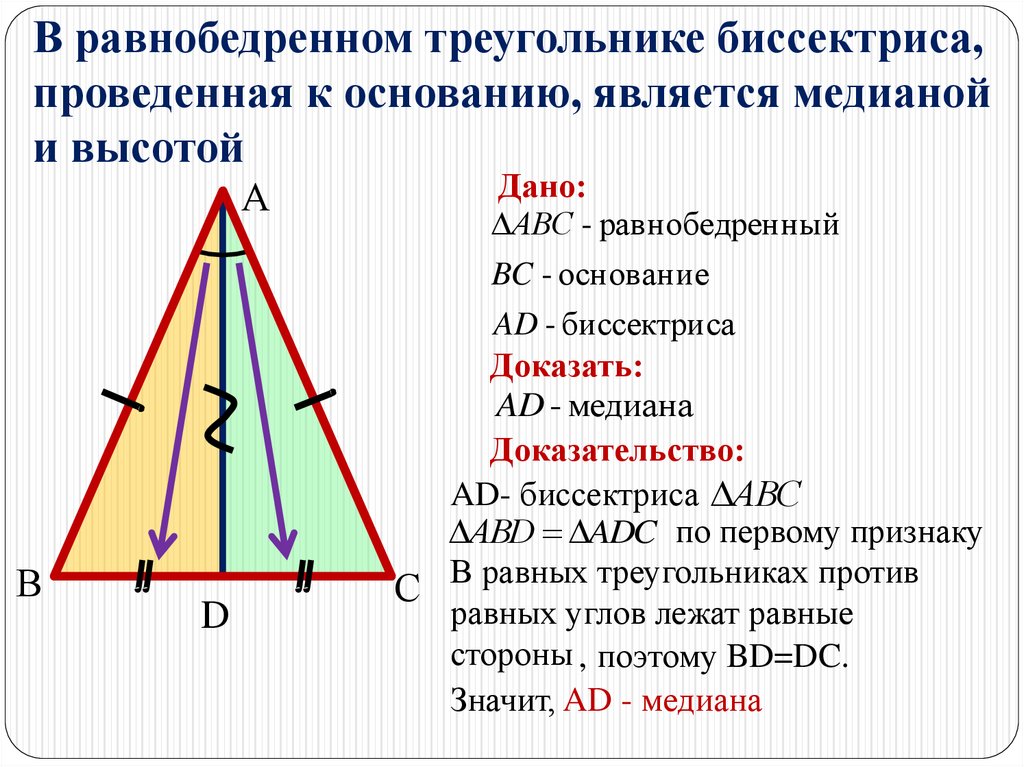
В равнобедренном треугольнике биссектриса,
проведенная к основанию, является медианой
и высотой
А
В
D
Дано:
АВС - равнобедренный
BC - основание
AD - биссектриса
Доказать:
AD - медиана
Доказательство:
AD- биссектриса АВС
АВD ADC по первому признаку
С В равных треугольниках против
равных углов лежат равные
стороны , поэтому BD=DC.
Значит, AD - медиана

10.

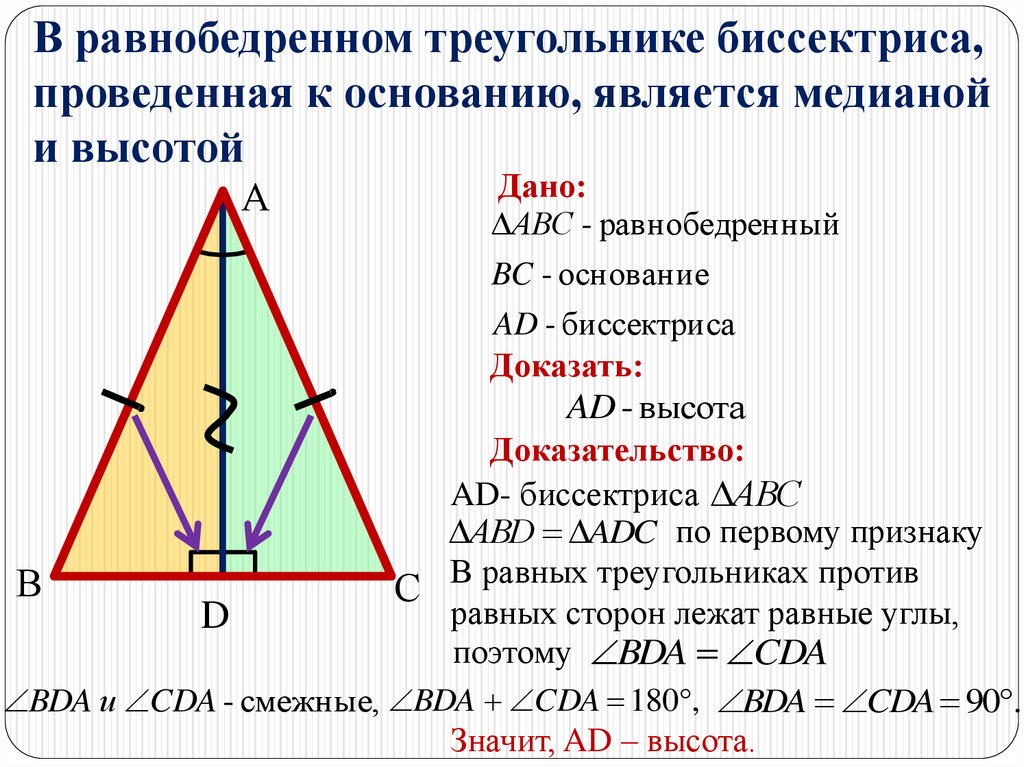
В равнобедренном треугольнике биссектриса,
проведенная к основанию, является медианой
и высотой
Дано:
АВС - равнобедренный
BC - основание
AD - биссектриса
Доказать:
AD - высота
Доказательство:
AD- биссектриса АВС
АВD ADC по первому признаку
В
С В равных треугольниках против
равных сторон лежат равные углы,
D
поэтому BDA CDA
BDA и CDA - смежные, BDA CDA 180 , BDA CDA 90 .
Значит, AD – высота.
А

11.

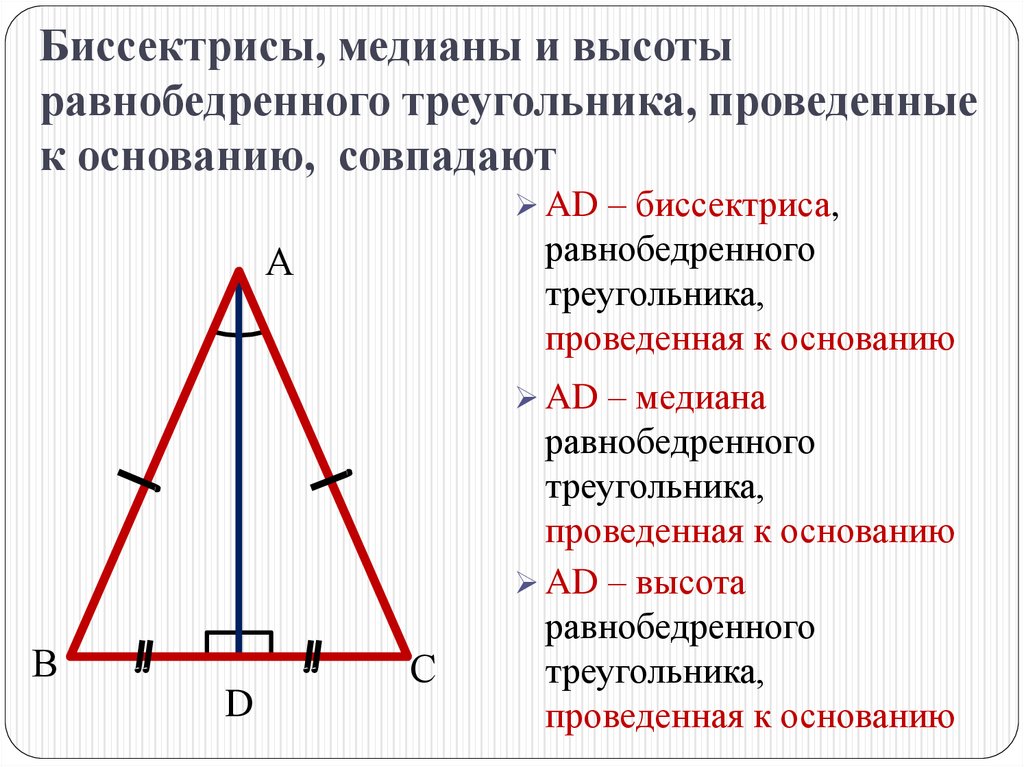
Биссектрисы, медианы и высоты
равнобедренного треугольника, проведенные
к основанию, совпадают
AD – биссектриса,
равнобедренного
треугольника,
проведенная к основанию
А
AD – медиана
В
D
С
равнобедренного
треугольника,
проведенная к основанию
AD – высота
равнобедренного
треугольника,
проведенная к основанию

12.

Чем отличается
свойство от
признака?
12

13.

Свойство --- это характеристика известного
объекта
(например, нам дан равнобедренный
треугольник, то из этого следует, что у него
углы при основании равны).
Признак --- это характеристика
неизвестного объекта, т.е.необходимо
определить что это за объект по каким-либо
признакам.
(например, если у треугольника углы при
основании равны, значит этот объект –
равнобедренный треугольник).

14.

Решение задач
В равнобедренном треугольнике боковая сторона равна
9см, а основание 5см. Вычислите периметр треугольника.
В равнобедренном треугольнике основание равно 7см, а
периметр равен 17см. Вычислите боковую сторону
треугольника.
В равнобедренном треугольнике боковая сторона равна
6см, а периметр 22см. Вычислите основание
треугольника.
В равностороннем треугольнике периметр равен 21см.
Вычислите сторону треугольника.

15.

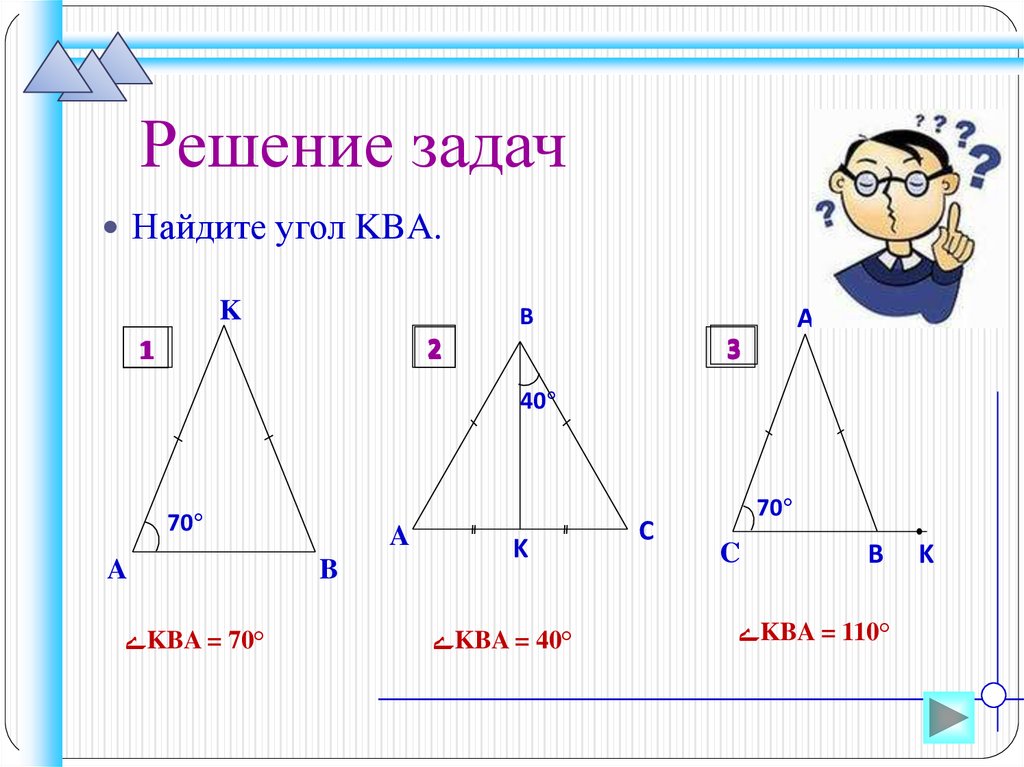
Решение задач
Найдите угол KBA.
K
B
A
2
1
3
40
70
A
‫ے‬KBA = 70°
A
B
K
‫ے‬KBA = 40°
C
70
C
B
‫ے‬KBA = 110°
K

16.

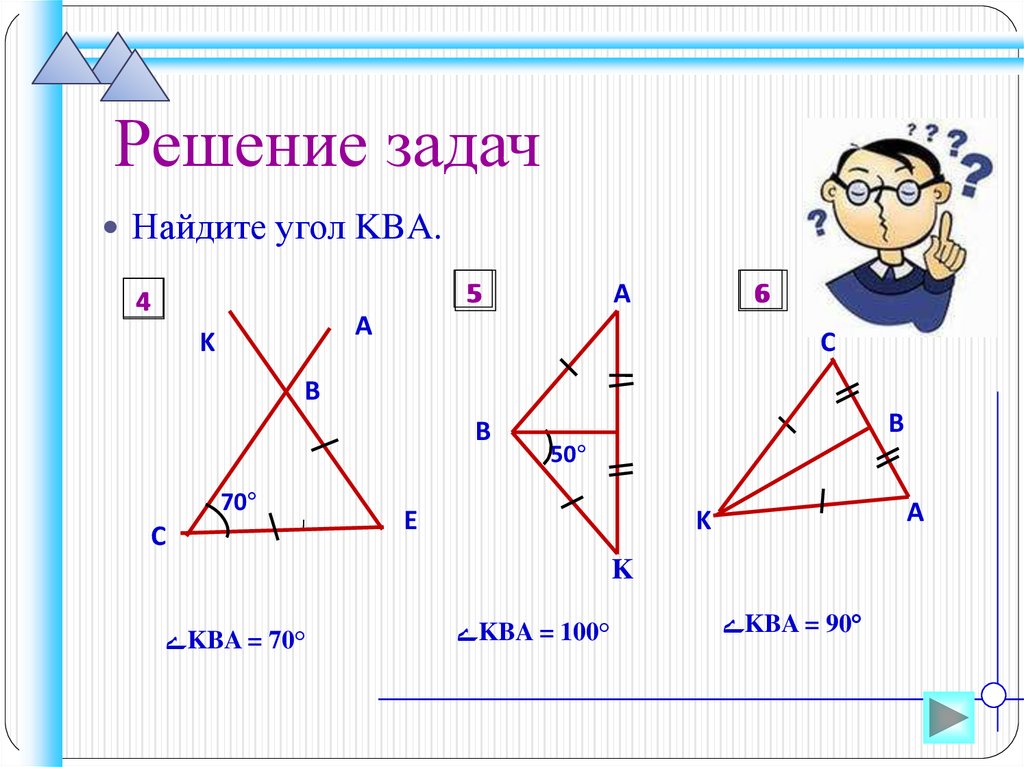
Решение задач
Найдите угол KBA.
5
4
A
6
A
K
C
B
B
70
C
B
50
E
A
K
K
‫ے‬KBA = 70°
‫ے‬KBA = 100°
‫ے‬KBA = 90°

17.

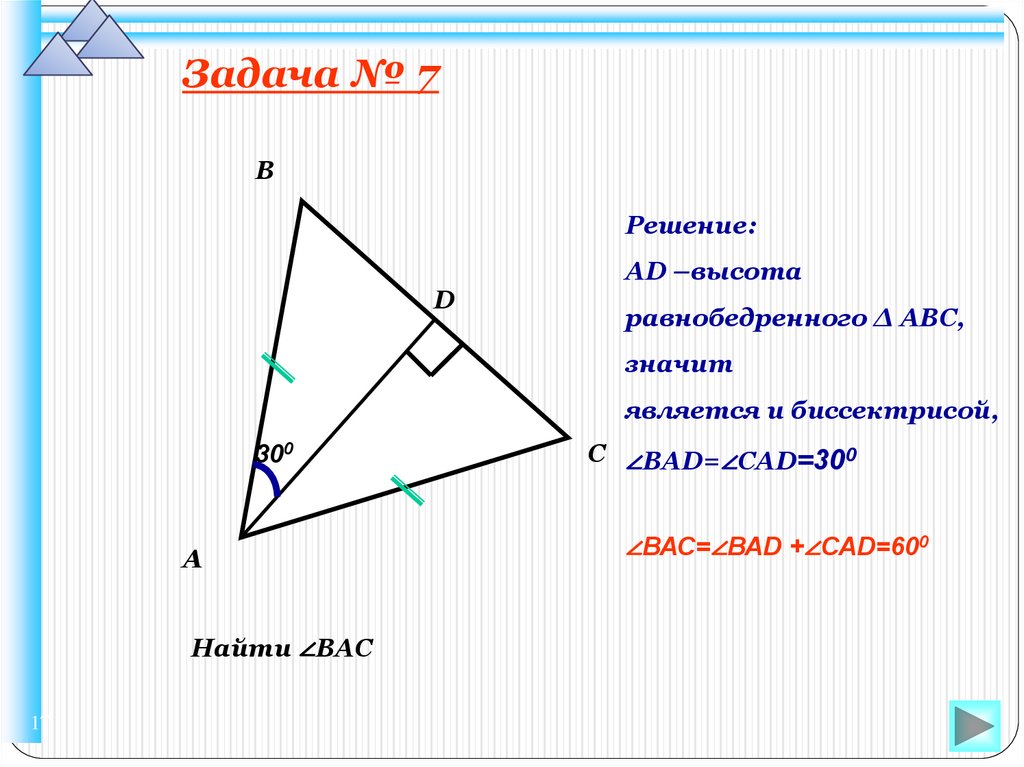
Задача № 7
В
Решение:
D
АD –высота
равнобедренного ∆ АВС,
значит
является и биссектрисой,
300
А
Найти ∠ВАС
17
С ∠ВАD=∠САD=300
∠ВАС=∠ВАD +∠САD=600

18.

Контрольные вопросы
Какой треугольник называется
равнобедренным?
Какой треугольник называется
равносторонним?
Является ли равносторонний треугольник
равнобедренным?
Каким свойством обладают углы
в равнобедренном треугольнике?
Каким свойством обладает биссектриса,
проведённая к основанию
равнобедренного треугольника?

19.

Домашнее задание
Изучить п. 18
№

20.

20