Промежутки возрастания и убывания функции. Точки экстремума

1. «Промежутки возрастания и убывания функции. Точки экстремума»

2. Содержание

Возрастающая
, убывающая
функции
Монотонная функция
Точки экстремума
Исследование функции на монотонность и
экстремум
Задача 1
Задача 2
Задания для самостоятельной работы

3. Возрастающая функция

Функция y = f(x) называется возрастающей
на некотором интервале,
u x2
если для любых x1
x1
таких, что
выполняется неравенство
x2 ,
f ( x1 ) f ( x 2 ).

4. Убывающая функция

Функция
y = f(x) называется
убывающей на некотором интервале,
если для любых
x
u
x
1
2
из этого интервала и таких, что
выполняется
x1 x 2
неравенство
f ( x1 ) f ( x2 ).

5. Монотонные функции

Функции,
возрастающие или
убывающие на
некотором интервале,
называются
монотонными.

6. На каждом интервале функция является монотонной

y=f(x)
а
x2
x1
x4
x3
b
x5
х

7.

Например,
функция у = f (х)
изображенная на рисунке, возрастает
на интервалах
(a; x1 ), ( x2 ; x3 ), ( x4 ; x5 )
и
убывает на интервалах
( x1 ; x 2 ),
( x3 ; x4 ),
( x5 ; b).

8. Максимумы, минимумы функции

x1 , x3 , x5
Точки
являются точками максимума,
а
x ,
x
точки
2
4
точками минимума.

9.

x0
Точка
называется точкой
максимума для функции
y=f(x),
если для любого х из
окрестности этой точки
выполняется
неравенство
f ( x) f ( x0 ).

10.

Точка
x0
называется точкой минимума
для функции
y=f(x),
если для любого х из
окрестности этой точки
выполняется неравенство
f ( x) f ( x0 ).

11. Экстремумы функции

Точки максимума и
минимума называются
точками экстремума

12. Дана функция у = f(х).

Чтобы исследовать функцию на
монотонность и экстремумы, нужно:
1. Найти область определения функции.
2. Найти производную данной функции.
3. Найти критические точки.
Критические точки - это точки, в
которых производная функции равна
нулю или не существует.
Т.е. чтобы найти критические точки,
нужно приравнять к нулю производную
функции и решить полученное
уравнение.
f ' ( x) 0.

13.

4. Отметить критические точки на числовой
прямой.
x1
x2
x3
x
5. Эти точки разбивают область определения
функции на некоторые интервалы.

14. Знак производной

Определить
знак производной функции
на каждом интервале.
Для этого нужно вычислить значение
производной в одной точке каждого
интервала
Определить его знак

15. Условие:

6. Если производная функции на данном
интервале положительная,
то функция на этом интервале возрастает,
Если производная функции на данном
интервале отрицательная,
то убывает.

16. Максимум функции

Если
производная
функции при переходе
через точку
x0
меняет
то -
x0
знак с "+" на "-",
точка
максимума

17. Минимум функции

Если
производная
функции при переходе
через точку
x0
меняет знак с "- '' на "+";
то
точка минимума
x0

18.

Если знак
производной в точке
x0
не меняется,
то в данной
критической точке
экстремума нет

19.

7. Найти значение функции в
точках экстремума, подставив
их абсциссы в данную
функцию.
8. Написать результат
исследования функции.

20. Задача 1.

Исследовать функцию
на монотонность и
экстремум.
1 3
2
f ( x) x x 3 x 4
3

21. Решение:

1 3
f ( x) x x 2 3 x 4
3
1. D( f ( x)) ( ; );
1 3
2
2
2. f ' ( x) x x 3x 4 x 2 x 3;
3
2
3. f ' ( x ) 0
x 2x 3 0
x1 1; x2 3;
'

22.

max
+
-1
min
-
+
3
х
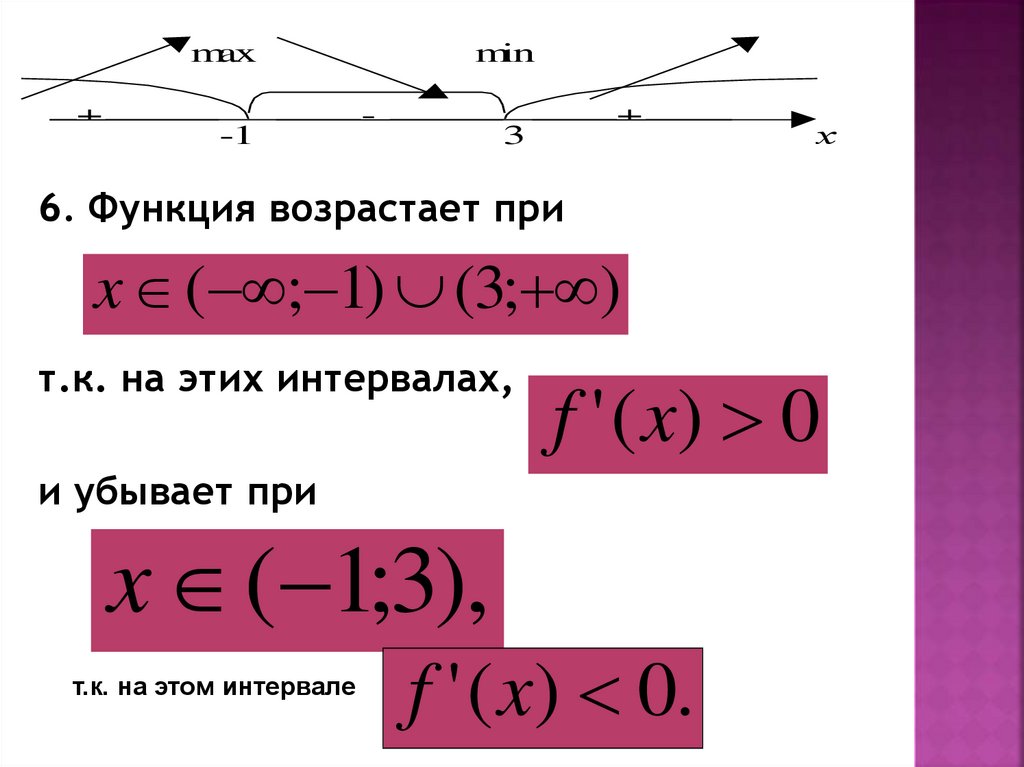
6. Функция возрастает при
x ( ; 1) (3; )
т.к. на этих интервалах,
f ' ( x) 0
и убывает при
x ( 1;3),
т.к. на этом интервале
f ' ( x) 0.

23.

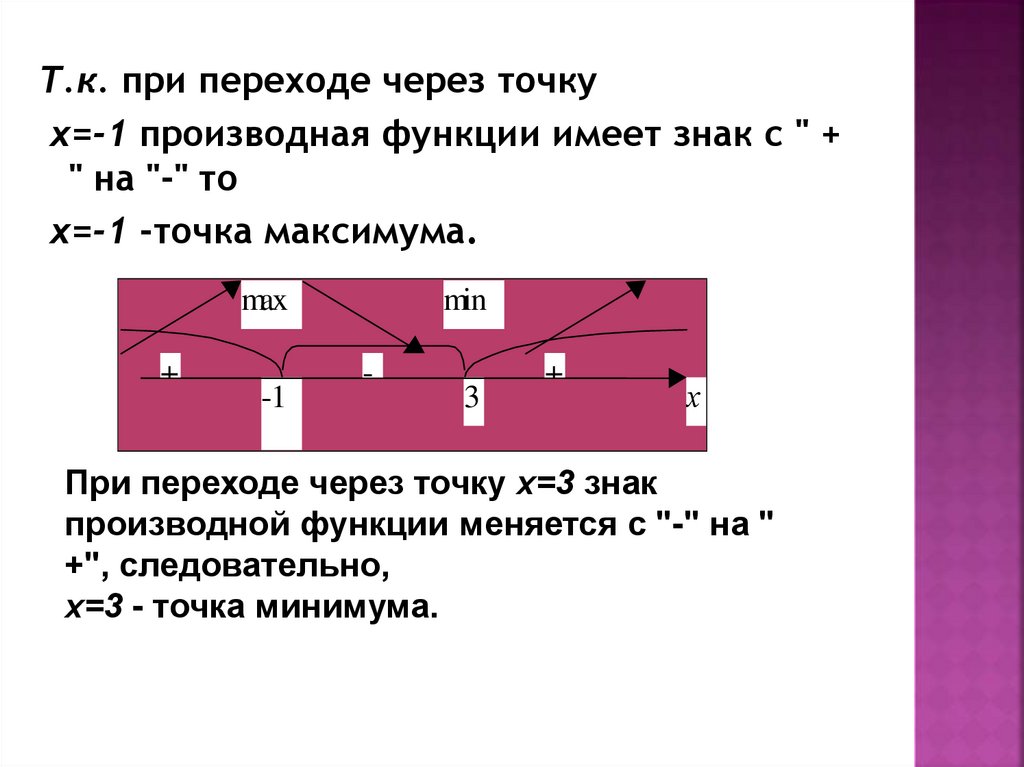
Т.к. при переходе через точку
х=-1 производная функции имеет знак с " +
" на "-" то
х=-1 -точка максимума.
max
+
-1
min
-
3
+
х
При переходе через точку х=3 знак
производной функции меняется с "-" на "
+", следовательно,
х=3 - точка минимума.

24. Значения функции в точках экстремума

1
1
2
3
2
7. f ( 1) ( 1) ( 1) 3 ( 1) 4 1 3 4 5 ,
3
3
3
1 3
f (3) 3 3 2 3 3 4 9 9 9 4 5;
3

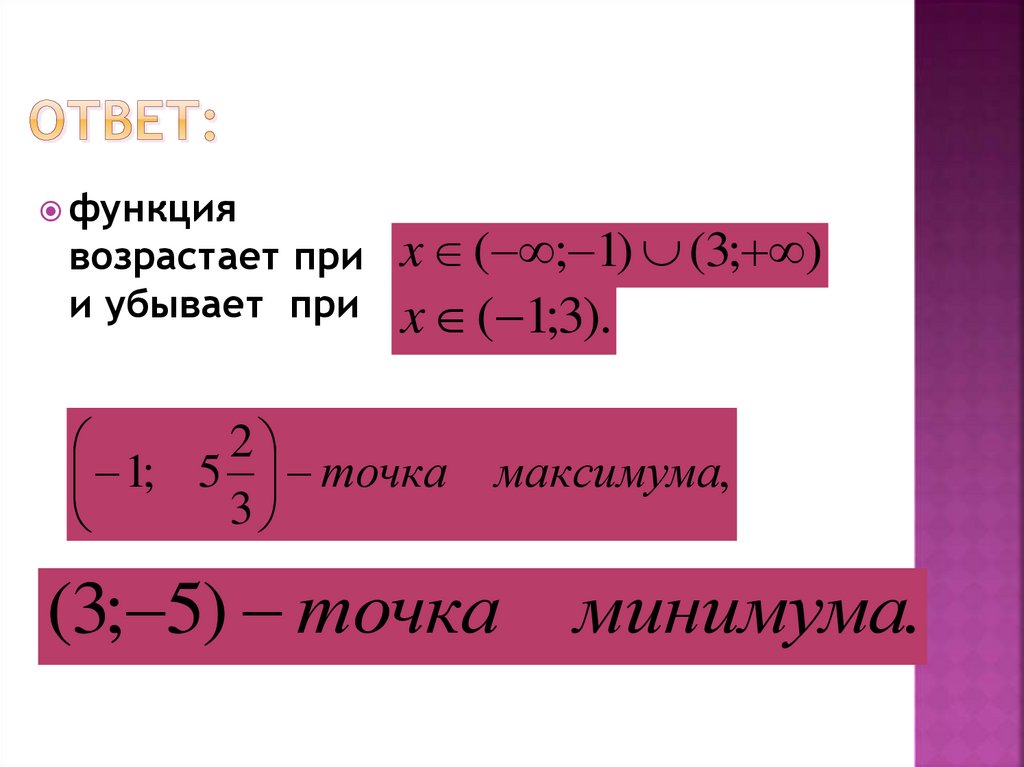
25. Ответ:

функция
возрастает при
и убывает при
x ( ; 1) (3; )
x ( 1;3).
2
1; 5 точка максимума,
3
(3; 5) точка
минимума.

26. Задача 2.

1 3 1 4
f ( x) x x
3
4
Исследовать
функцию
на монотонность и экстремум.

27. Решение:

1. D( f ( x)) ( ; );
'
1 3 1 4
2. f ' ( x ) x x x 2 x 3 ;
4
3
3. f ' ( x ) 0 x 2 x 3 0
x1, 2 0;
x3 1;
4. f ' ( 1) 1 ( 1) 2 0
2
3
1
1 1 1
f ' 0
8
2 2 2
f ' (2) 2 2 2 3 4 0;

28.

max
+
0
+
1
-
6. Функция возрастает при
x ( ;1)
т.к. на этих интервалах
f ' ( x) 0
и убывает при
x (1; ),
т.к. на этом интервале
f ' ( x) 0.
х

29.

Т.к.
при переходе через точку х=0
производная функции не меняет знак, то
в точке х=0 функция экстремума не
имеет.
При переходе через точку х=1 знак
производной функции меняется с "+" на "
-", следовательно, х=1 - точка максимума.

30. Ответ: функция возрастает при и убывает при

1 3 1 4 1
7. f (1) (1) (1) ,
3
4
12
x ( ;1)
1
1; точка
12
1
1; точка max .
12
x (1; ).
максимума.

31.

Задания для самостоятельной работы:
исследовать функцию
на монотонность и экстремум