Similar presentations:
Нахождение промежутков монотонности (промежутков возрастания и убывания)
1.
Нахождениепромежутков
монотонности
(промежутков
возрастания и
убывания)
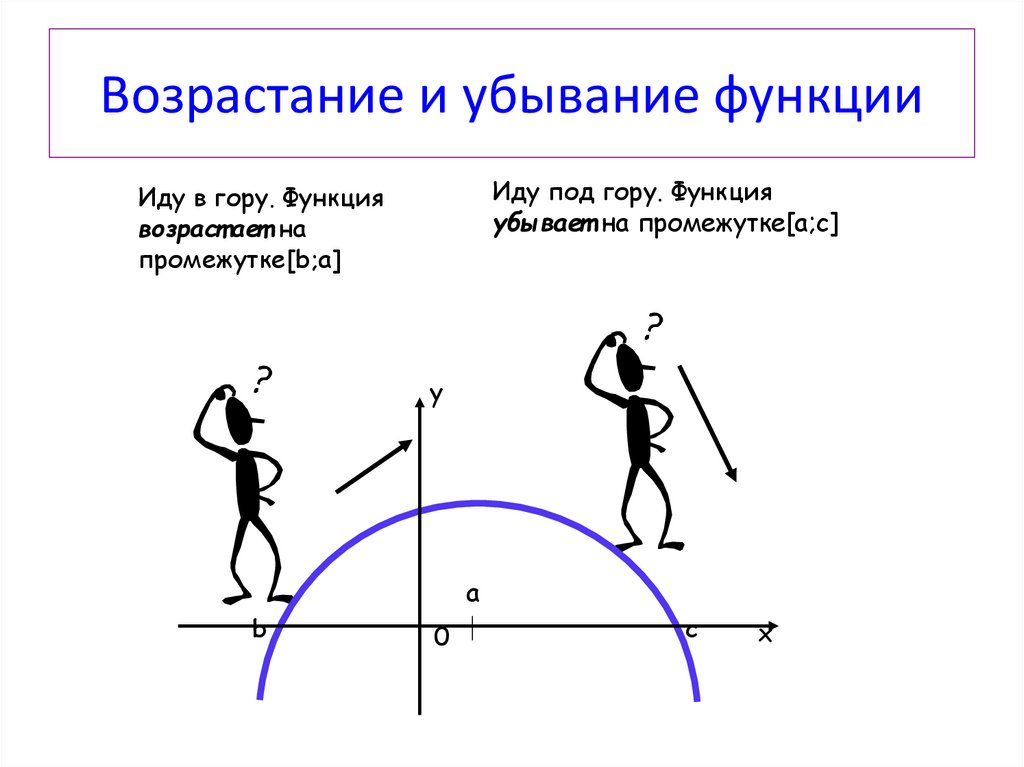
2. Возрастание и убывание функции
Иду под гору. Функцияубывает на промежутке[a;с]
Иду в гору. Функция
возраст ает на
промежутке[b;a]
y
a
b
0
c
x
3. Чтобы найти промежутки монотонности функции f(x), надо:
1. Найти f´(x).2. Найти нули и точки разрыва f´(x).
3. Определить, где f´(x)>0. Это промежутки
возрастания f(x).
4. Определить, где f´(x)<0. Это промежутки
убывания f(x).
Промежутки монотонности записываются в квадратных
скобках, если концы их входят в область определения
функции.
4. Задание 1:
Найти промежутки монотонностифункции
9х 1
у
х
2
5. ЭКСТРЕМУМЫ ФУНКЦИИ
6. Признак максимума функции
• Если функция f непрерывна в точке х0, а f `(x) > 0 наинтервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0
является точкой максимума функции f.
• Если в точке х0 производная меняет знак с плюса на минус, то
точка х0 максимума.
10
+
9
Y
-
8
7
+
6
-
5
4
+
-
3
2
1
X
-10
-9
-8
-7
-6
+
-5
-4
-3
-2
-1
0
-1
-2
-3
+
-4
1
2
3
4
-
-5
-6
+
-7
-8
-9
-10
-
5
6
7
8
9
10
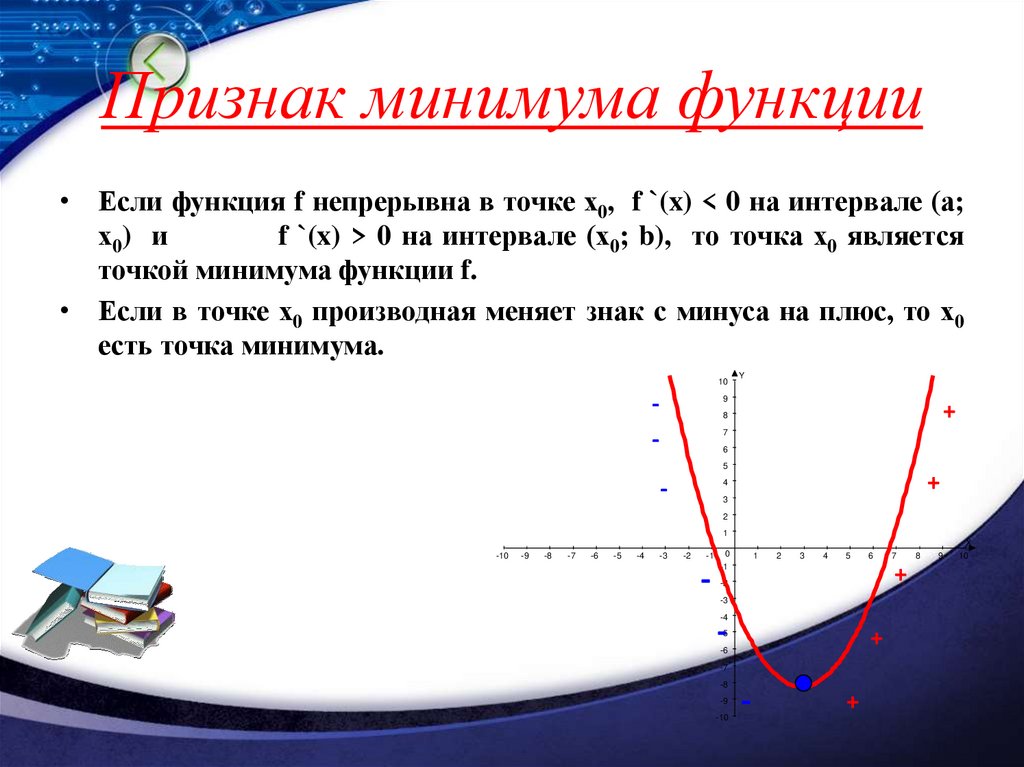
7. Признак минимума функции
• Если функция f непрерывна в точке х0, f `(x) < 0 на интервале (а;х0) и
f `(x) > 0 на интервале (х0; b), то точка х0 является
точкой минимума функции f.
• Если в точке х0 производная меняет знак с минуса на плюс, то х0
есть точка минимума.
10
-
Y
9
+
8
7
6
5
-
+
4
3
2
1
X
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
-
0
1
2
3
4
5
6
+
-1
-2
-3
-4
-
+
-5
-6
-7
-8
-9
-10
7
-
+
8
9
10
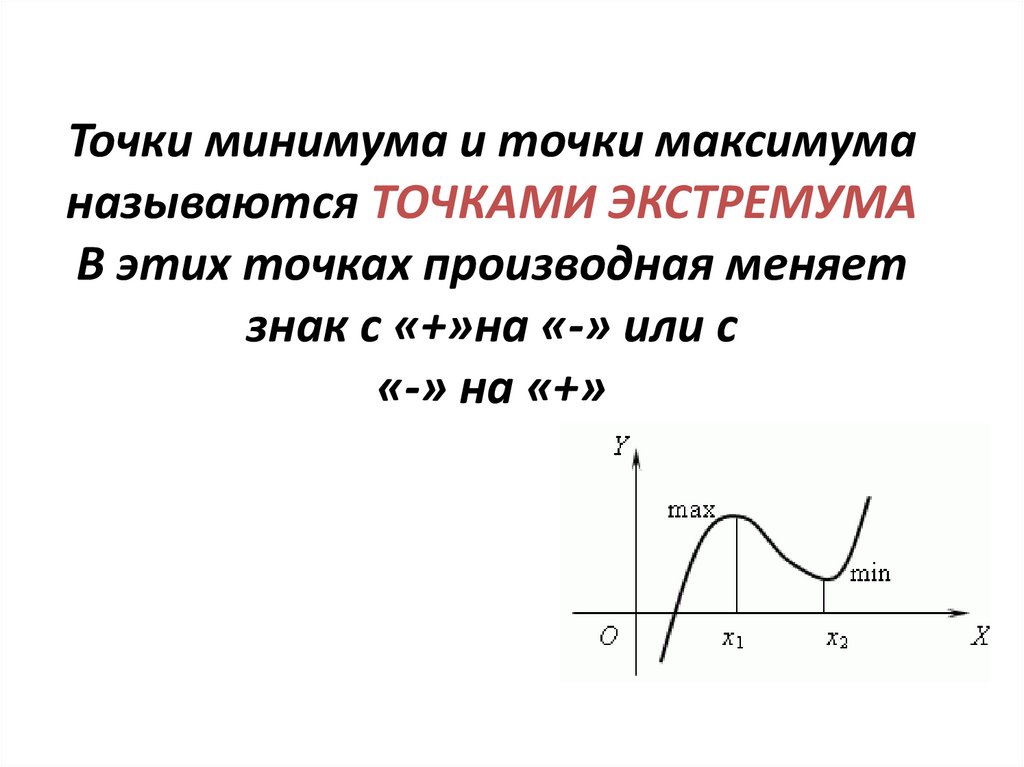
8. Точки минимума и точки максимума называются ТОЧКАМИ ЭКСТРЕМУМА В этих точках производная меняет знак с «+»на «-» или с «-» на
«+»9.
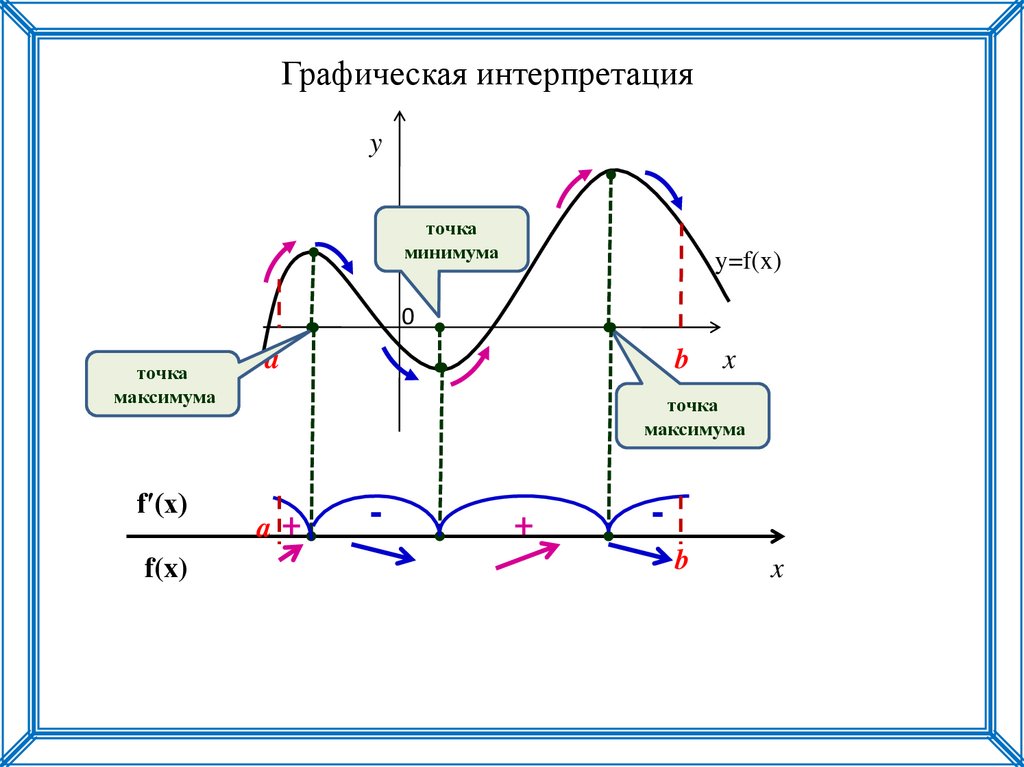
Графическая интерпретацияy
точка
минимума
y=f(x)
0
точка
максимума
f′(x)
f(x)
b
a
x
точка
максимума
a+
-
+
b
x
10.
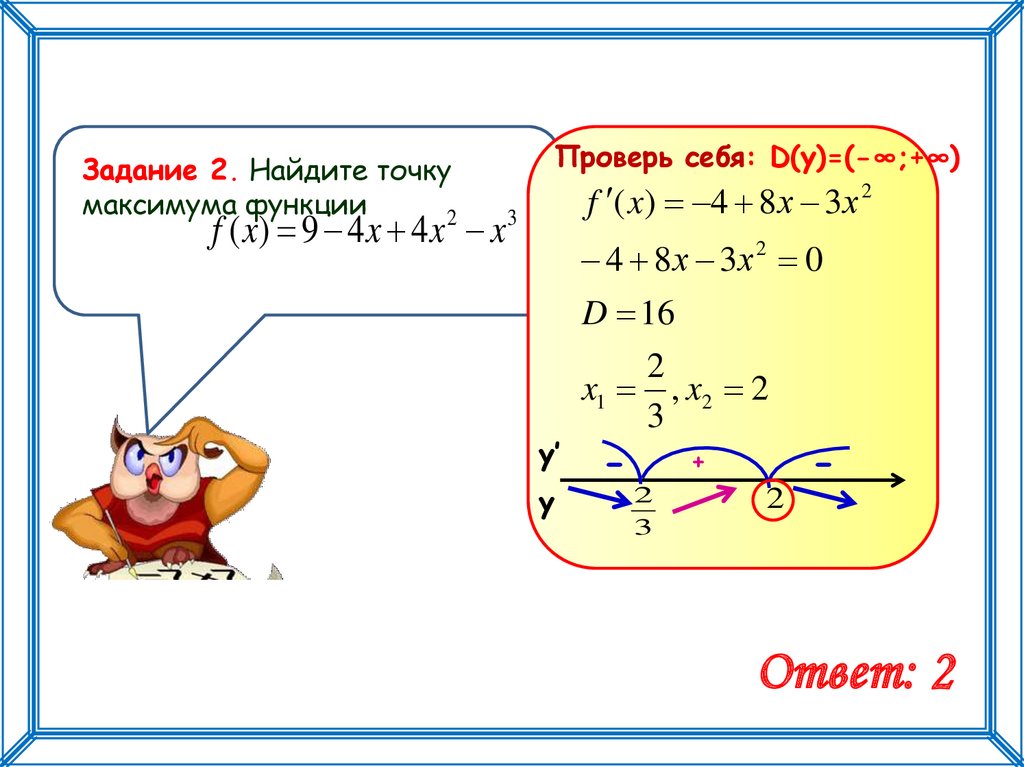
Проверь себя: D(y)=(-∞;+∞)Задание 2. Найдите точку
максимума функции
2
f ( x) 4 8 х 3 х 2
f ( x) 9 4 x 4 x x 3
4 8 х 3х 2 0
D 16
у′
у
2
x1 , x2 2
3
-
+
2
3
-
2
Ответ: 2
11. Производная и графики функций
12. Общая схема исследования функций
1) находят область определения функции;2) определяют точки разрывов функции и их характер;
3) находят корни функции;
4) определяют четность или нечетность функции;
5) проверяют функцию на периодичность;
6) вычисляют производную функции, находят ее критические точки, находят
интервалы монотонности и экстремумы;
7) вычисляют вторую производную функции и по ней определяют интервалы
выпуклости, вогнутости и точки перегиба;
8) находят асимптоты функции;
9) по полученным данным строят качественный график исследуемой функции.
13.
Исследовать функцию ипостроить её график:
у=х3-6х2+9х+1
14. 1. Найти производную функции
у=х3-6х2+9х+1Y’=3x2-12x+9
15. 2. Найти критические точки
х1=3Х2=1
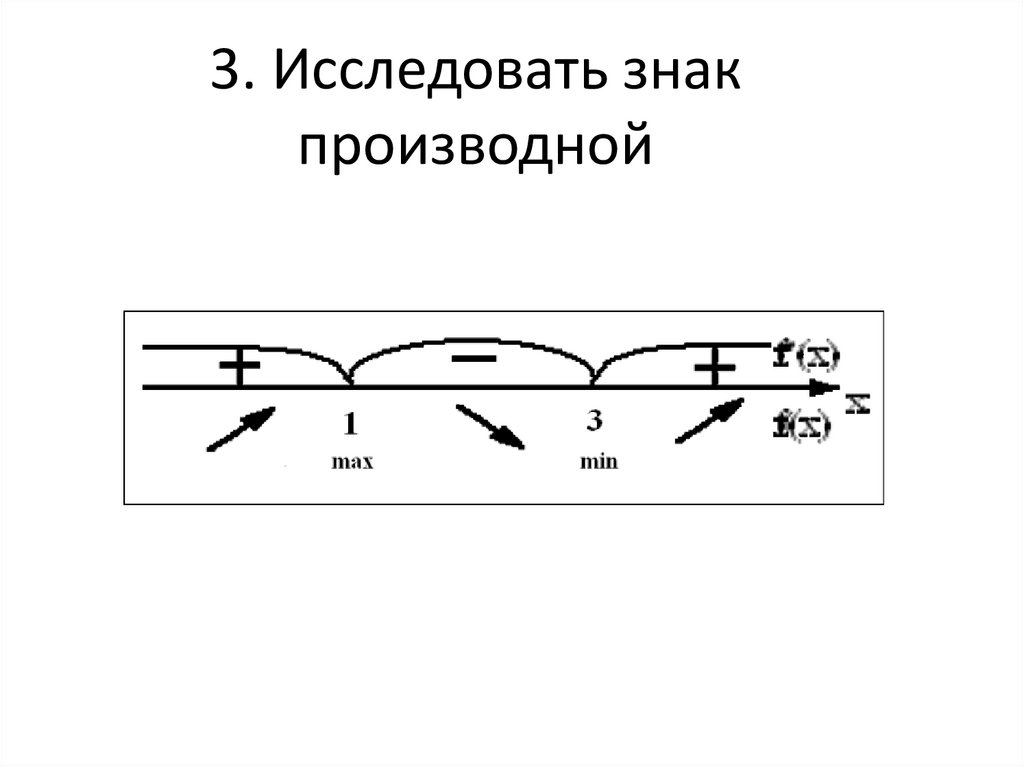
16. 3. Исследовать знак производной
17. 4. Найти экстремальные значения функции
у=х3-6х2+9х+1уmax(1)=5
уmin(3)=1
18. 5. Найти вторую производную
у=х3-6х2+9х+1Y’’=6x-12
19. 6. Найти точки в которых вторая производная равна нулю или не существует
Х1=220. 7. Исследовать знак второй производной
Х=2 – точка перегиба21. 8. Найти значение функции в точке перегиба
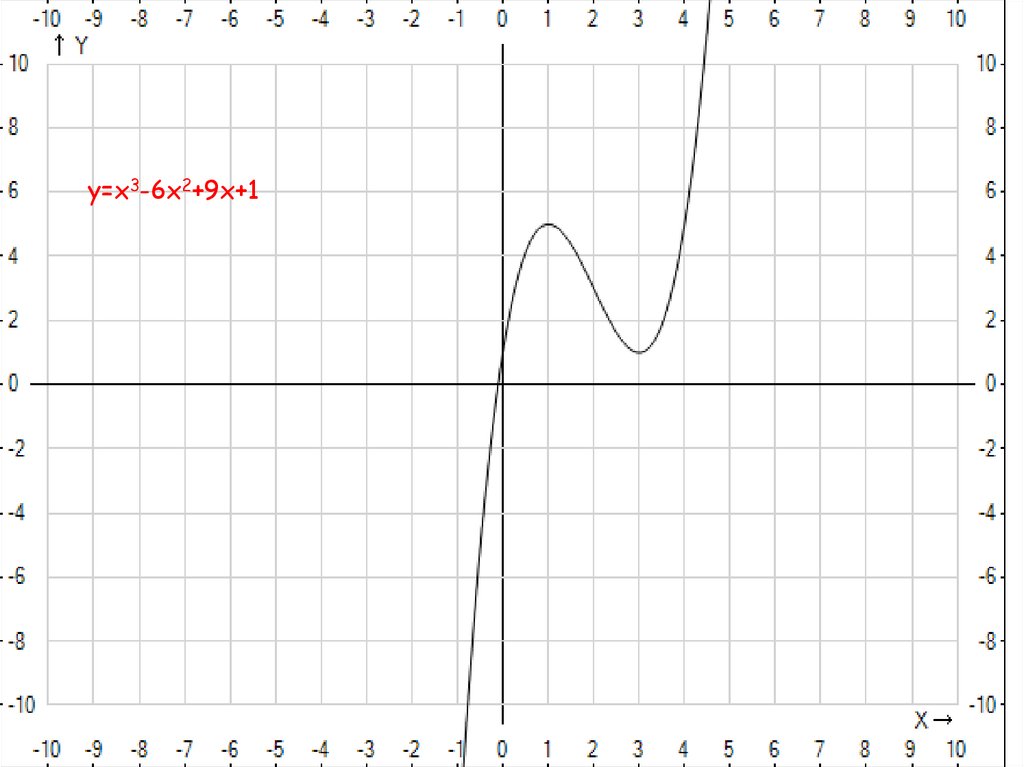
у (2)=322. 9. Построение графика функции у=х3-6х2+9х+1
у=х3-6х2+9х+123. ПРИМЕР
Задание 3: Исследовать функцию ипостроить график
f ( x ) 3x x
2
3
















 mathematics
mathematics








