Возрастание и убывание функции. Экстремумы

1. Тема урока: Возрастание и убывание функции. Экстремумы.

2. Понятие «Функция»

Функция 1692 г
Готфрид Вильгельм
Лейбниц
1698 г. Якоб Бернулли
начало XIX века Николай Иванович Лобачевский

3.

Линейная y=kx+b
y
S=vt
vx=v0x+axt
o
x
k>0
b
y
tф=1,8tc+32
k<0
0
x
b

4. Квадратичная y=ax2+bx+c y=a (x - m)2 +n

y
y=a (x - m)2 +n
n
a>0
-1
0
0
1
2
3
4
5
6
x
m
g 2
S (t ) t v0t
2
y
R
a<0
n
I
Q=RI2
в единицу
времени
0
-1
0
1
2
3
4
m
5
6
7
8
9
10
11
7
x

5. Степенная функция y=axn

Степенная функция
V x
3
n
y=ax
y
Y=x3
-3
-2
-1
0
o
1
2
3
y
2
T
X
q
1
2
y x
1
2
o
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
x
0,8
x

6. Прогноз погоды

Температура T(t)
Давление атмосферное p(t)
0
-2
17
18
19
20
-4
-6
-8
-10
-12
-14
-16
21
22
766
764
762
760
758
756
754
752
750
748
746
17
-18
Дни
18
19
20
дни
21
22

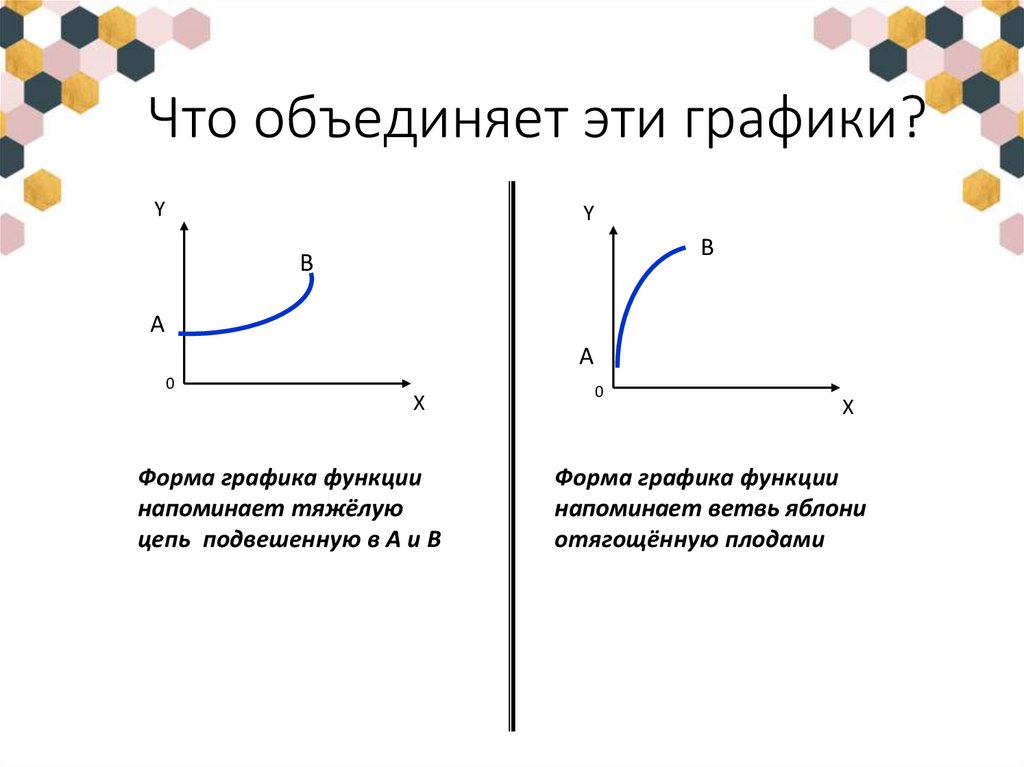
7. Что объединяет эти графики?

Y
Y
B
B
A
A
0
X
Форма графика функции
напоминает тяжёлую
цепь подвешенную в A и B
0
X
Форма графика функции
напоминает ветвь яблони
отягощённую плодами

8.

Андрей Николаевич Колмогоров
(1903-1987)
•Алгебра и начала анализа
10 - 11 класс.
•Математическая логика.
•Математическая статистика.
•Функциональный анализ.
•Теория информации.
•Математика в стрельбе.
•Математика в лингвистике.
•Математика в биологии.

9. Элементарные функции

•Линейные
•Квадратичные
•Степенные
•Дробно-линейные
•Тригонометрические

10. Элементарные функции.

Линейные
Квадратичная
y
y
y=a(x-m)2+n2
y=kx+b
b
m
x
0
0
x
n
Дробно - линейные
y
k
y
n
x m
Степенная
y=xn
y
x
0
n=2k
y=n
x=m
n -чётное
0
x

11. Элементарные функции. Тригонометрические.

y=sin(x)
y=cos(x)
0
y=tg(x)
y=ctg(x)

12.

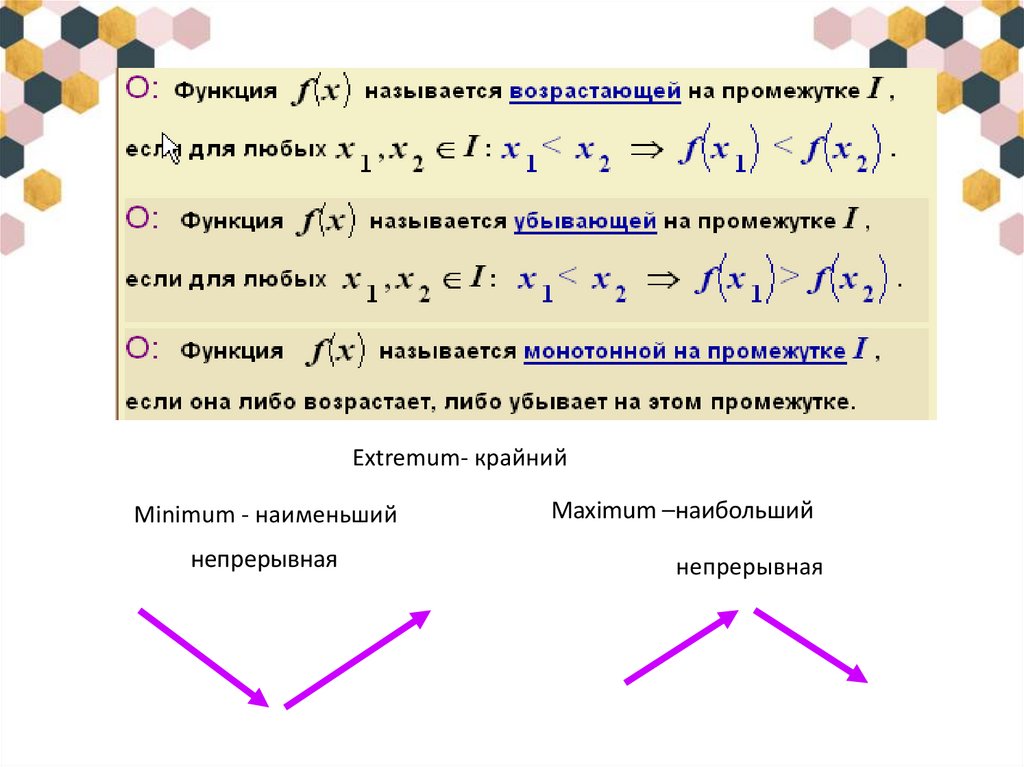
Extremum- крайний
Minimum - наименьший
непрерывная
Maximum –наибольший
непрерывная

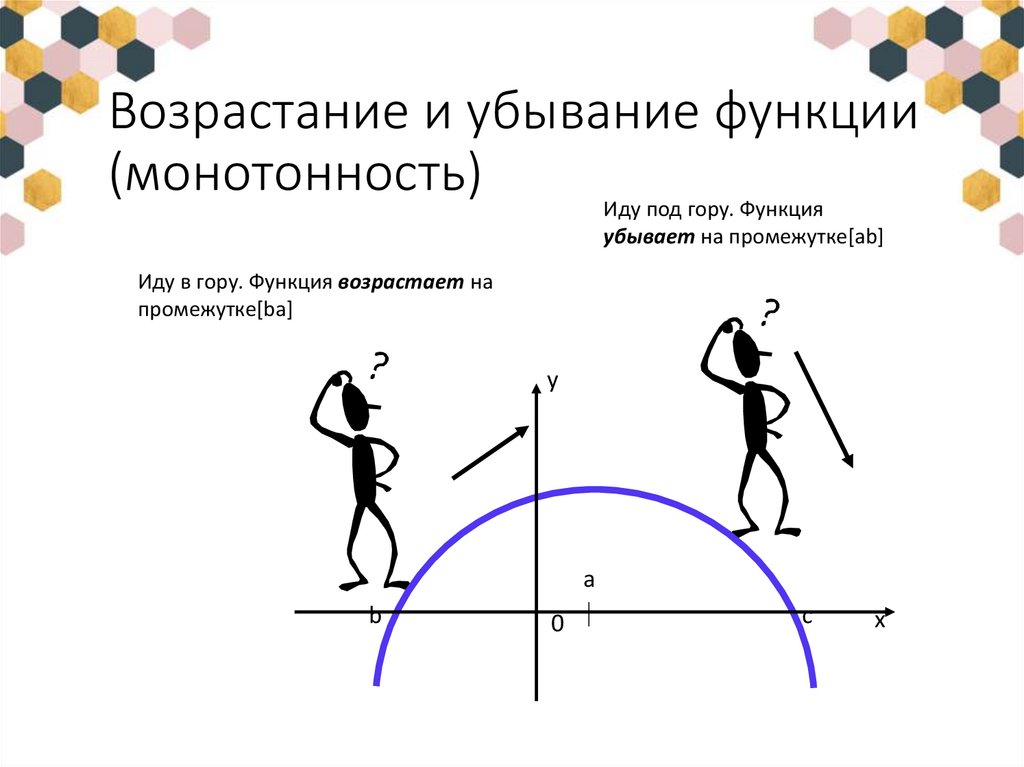
13. Возрастание и убывание функции (монотонность)

Иду под гору. Функция
убывает на промежутке[ab]
Иду в гору. Функция возрастает на
промежутке[ba]
y
a
b
0
c
x

14. Maximum – наибольший Minimum - наименьший

Maximum
Minimum
Max
Min
X0
x0
x0
x0

15. Экстремумы

Минимум (min)
Максимум (max)
Y
Y
0
X
0
X

16.

Эталон (знаковая модель)
Иду под гору. Функция
убывает на промежутке
[a;c]
Иду в гору. Функция
возрастает на
промежутке [b;a]
y
Функция
a
b
НЕ Функция
c
0
x
y
y
Минимум (min)
Максимум (max)
m
0
x
0
n
Y
Непрерывная
y
Y
x
y
0
X
X
Y=m
X=n
x

17. Maximum, наибольший Minimum, наименьший

y
x3
x1
x2
0
xmax=x2
Max не всегда наибольший
Xнаиб =x4
Min не всегда наименьший
xнаим= x4
xmin= x3
Точки экстрема xmax и xmin
Экстрем функции ymax=f(xmax), ymin=f(xmin)
x4
x

18. Экономическая задача.

Кривая предложения S=S(p)
Кривая спроса D=D(P)
60
400
350
300
250
200
150
100
50
0
50
40
30
20
10
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

19. Формирование стоимости

100
80
Крив ая
спроса D=D(P)
60
40
Крив ая
предложения
S=S(p)
20
0
1
2
3
4
5
6
7
8
9

20. Формирование реальной стоимости

100
80
Крив ая
спроса D=D(P)
60
40
Крив ая
предложения
S=S(p)
20
0
1
2
3
4
5
6
7
8
9