Функция у=ах² , её свойства и график. 8 класс

1.

Функция у=ах² ,
её свойства и
график.
8 класс

2.

3.

у=х²
Графиком является парабола.
х
Точка
(0;0)
-1
0 –1вершина
2 параболы
3
-2
Ветви направлены вверх
1
4
9
1
4
У
0
Ось у- ось симметрии
у
Ветвь
9
Ветвь
Построим график функции
-3
9
у=х² для этого значения
параболы
параболы
аргумента
(х) выберем
2
сами, а значенияу функции
х
(у) вычислим4 по формуле
у=х².
Ось
симметрии
х
Вершина параболы
01 2 3
1
-3 -2 -1

4.

Постройте график
функции:
y=
2
2x
х - 2 -1 0 1 2
у 8 2 0 2 8
Постройте график
функции:
y = 0,5x2
у
у х
9
8
7
6
5
4
3
2
1
-3 -2 -1 0
х - 3 - 2 -1 0 1 2 3
у 4,5 2 0,5 0 0,5 2 4,5
у 2х
2
у 0,5х
1
2 3
2
2
х

5.

График функции у=аx2 может быть
получен из графика функции у=x2
путем растяжения его вдоль оси Оу
в а раз (а-натуральное число).

6.

Зависимость «степени крутизны »
параболы от коэффициента а.
у
у х
y =9 аx2
y = аx2
0 < а <1
8
7
а
6
5
4
3
2
1
-3 -2 -1 0
>1
у 2х
2
у 0,5х
1
2 3
2
2
х

7.

Свойства функции у=ах²
1.Область
1. D ( у ) ;
определения
2.
2.Область
значений
3. у=0, если х= 0
E ( у ) 0;
у>0, если
х ; 0
0;
(а>0):
у
8
6
4
2
1
4. Функция убывает
при х ; 0
х
Функция возрастает -3 -2 -1 0 1 2 3
-1
при х 0 ;
ограничена снизу, но не ограничена
5.Функция
Ограниченность
сверху.
унаиб.= НЕТ
6. унаим.= 0
Непрерывна.
7. Непрерывность
7.

8.

По графику функции
у=2х² найдите
значение функции,
соответствующее
заданному значению
аргумента:
1)
2)
3)
4)
4)
0 у=0
1 у=2
-1 у=2
2 у=8
-1,5 у=4,5
у
у 2х
9
8
7
6
5
4
3
2
1
-3 -2 -1 0
1
2 3
2
х

9.

Найдите
унаиб. и унаим.
функции у=2х²
на отрезке
2
8
0 ; 2
Унаиб.=8
Унаим.=0
у 2х
у
4
1
-3 -2 -1
01 2 3
х

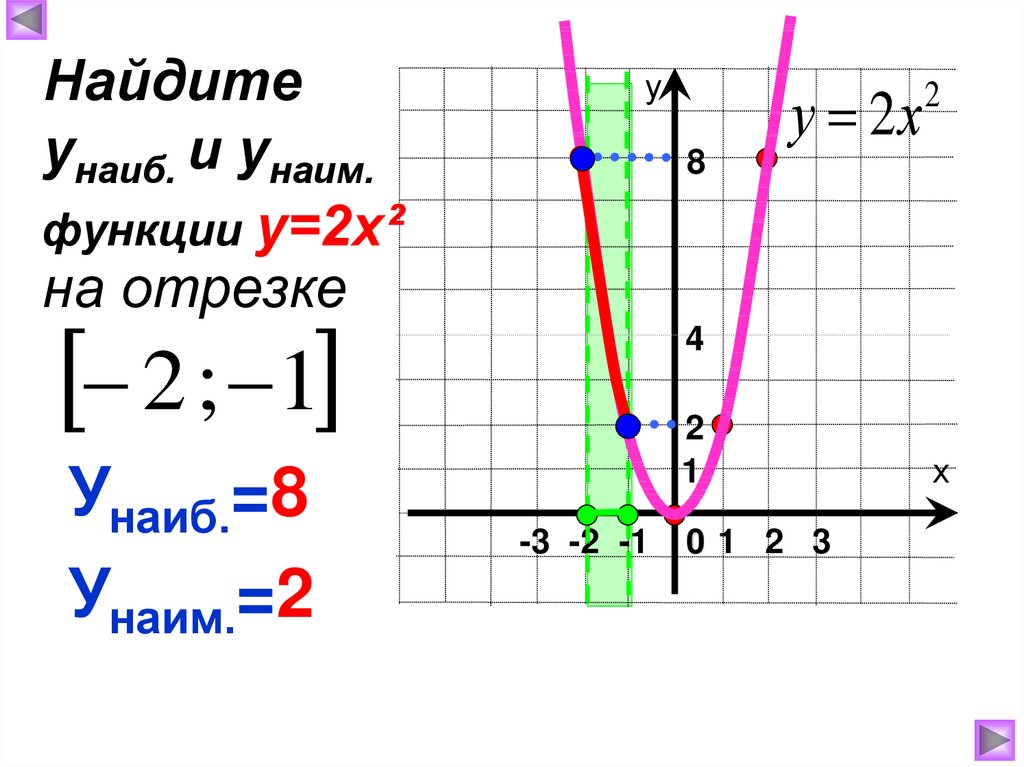
10.

Найдите
унаиб. и унаим.
функции у=2х²
на отрезке
у
8
2 ; 1
Унаиб.=8
Унаим.=2
у 2х
2
4
2
1
-3 -2 -1
01 2 3
х

11.

Найдите
унаиб. и унаим.
функции у=2х²
на отрезке
1;1,5
Унаиб.=4,5
Унаим.=0
у
у 2х
2
8
4,5
3
2
1
-3 -2 -1
х
01 2 3

12.

Построим график функции
у=-х² для этого значения
аргумента (х) выберем
сами, а значения функции
(у) вычислим по формуле у=х².

13.

у=-х²
Графиком является парабола.
х
-1
0 –1вершина
2 параболы
3
-2
Точка
(0;0)
Ветви
направлены
вниз
-1
-4
-4
У
0 симметрии -9 -1
Ось у- ось
у
Вершина параболы
х
-3 -2 -1 0 1 2 3
-1
-4
Ось
симметрии
-9
у х
2
-3
-9

14.

График функции у=ах2 симметричен
графику функции у=-ах2 относительно
оси Ох.
Если а>0, то ветви параболы
направлены…
Если а<0, то ветви параболы
направлены…

15.

y=
2
-2x
х - 2 -1 0 1 2
у -8 -2 0 -2 -8
Постройте график
функции:
y = -0,5x2
у
-3 -2 -1 0
1
-1
-2
-3
-4
-5
-6
-7
-8
-9
х - 3 - 2 -1 0 1 2 3
у -4,5 -2 -0,5 0 -0,5 -2 -4,5
2 3
х
Постройте график
функции:
у 0,5х
у 2х
2
у х
2
2

16.

График функции у= 1 x2 может
а
быть получен из графика функции
у=x2 путем сжатия его вдоль оси Оу
в а раз (а-натуральное число).

17.

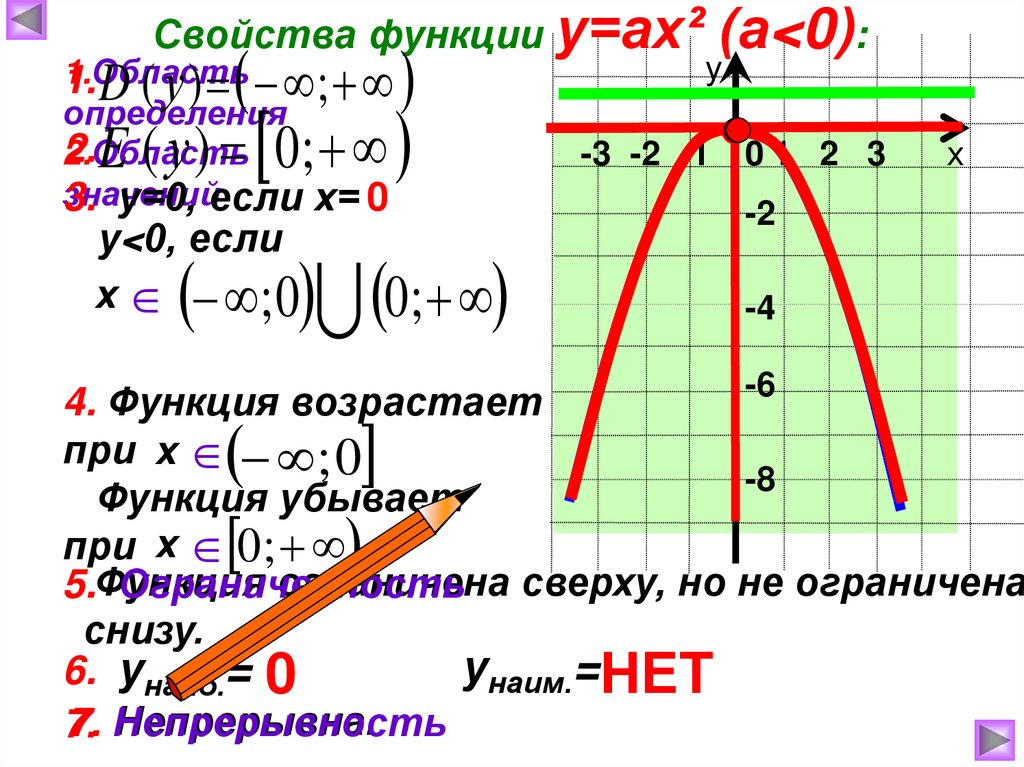
Свойства функции у=ах²
1.Область
1. D ( у ) ;
определения
2.
2.Область
значений
3. у=0, если х= 0
E ( у ) 0;
у<0, если
х ; 0
0;
(а<0):
у
-3 -2 -1
01 2 3
х
-2
-4
-6
4. Функция возрастает
при х ; 0
-8
Функция убывает
при х 0 ;
ограничена сверху, но не ограничена
5.Функция
Ограниченность
снизу.
унаим.=НЕТ
6. унаиб.= 0
Непрерывна.
7. Непрерывность
7.

18.

Найдите
унаиб. и унаим.
функции у=-0,5х²
на отрезке
у
х
-4 -3 -2 -1 0 1 2 3 4
-1
-2
у 0,5х2
0 ; 2
-4
Унаиб.=0
Унаим.=-2
-8
-6

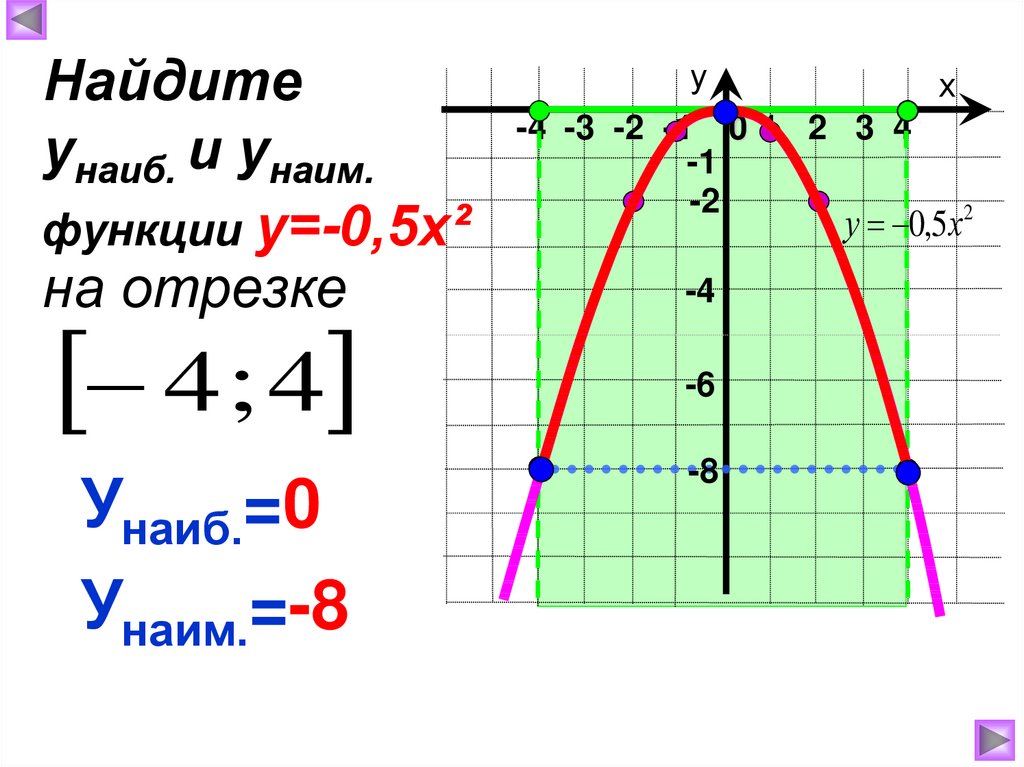
19.

Найдите
унаиб. и унаим.
функции у=-0,5х²
на отрезке
у
х
-4 -3 -2 -1 0 1 2 3 4
-1
-2
2
у 0,5х
4 ; 4
-4
Унаиб.=0
Унаим.=-8
-8
-6

20.

Найдите
-4
унаиб. и унаим.
функции у=-0,5х²
на полуинтервале
2 ; 4
Унаиб.=-2
Унаим.=НЕТ
у
х
-3 -2 -1 0 1 2 3 4
-1
-2
2
у 0,5х
-4
-6
-8

21.

Найдите
-4
унаиб. и унаим.
функции у=-0,5х²
на полуинтервале
у
х
-3 -2 -1 0 1 2 3 4
-1
-2
2
у 0,5х
2 ; 2
-4
Унаиб.=0
Унаим.=-2
-8
-6

22.

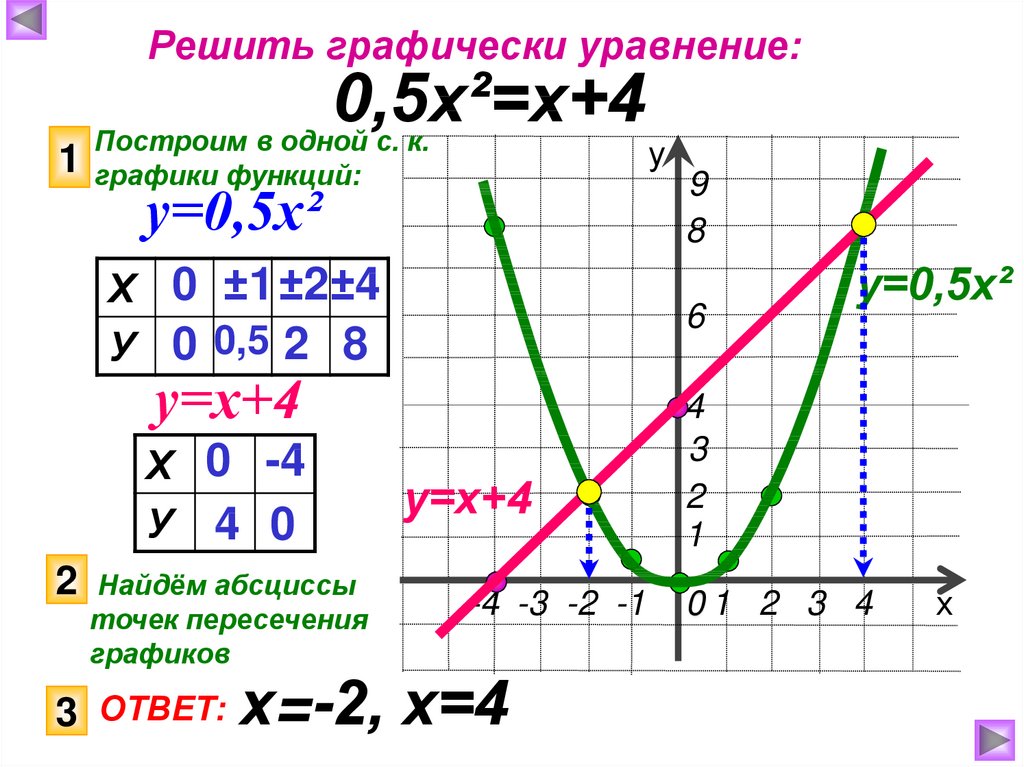
Решить графически уравнение:
1
0,5х²=х+4
Построим в одной с. к.
графики функций:
у=0,5х²
Х 0 ±1 ±2±4
У 0 0,5 2 8
2
Найдём абсциссы
точек пересечения
графиков
3 ОТВЕТ:
9
8
6
у=х+4
Х 0 -4
У 4 0
у
у=х+4
-4 -3 -2 -1
х=-2, х=4
у=0,5х²
4
3
2
1
01 2 3 4
х

23.

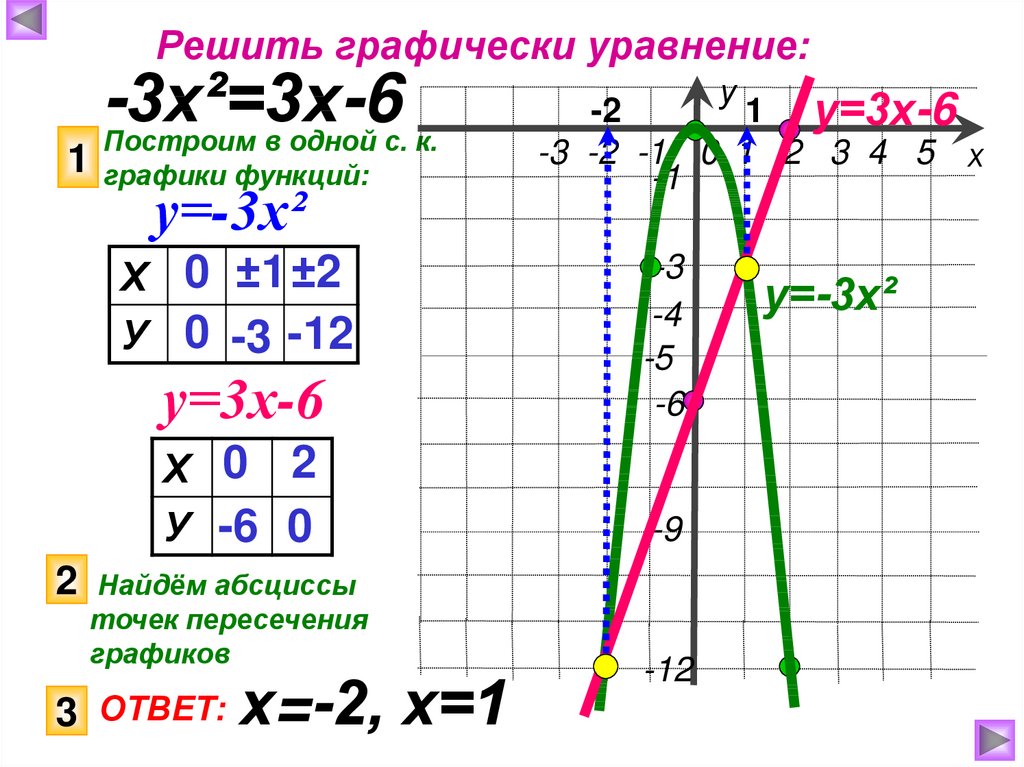
Решить графически уравнение:
1
-3х²=3х-6
Построим в одной с. к.
графики функций:
у=-3х²
Х 0 ±1 ±2
У 0 -3 -12
2
у
-2
1 у=3х-6
-3 -2 -1 0 1 2 3 4 5 х
-1
у=3х-6
-3
-4
-5
-6
Х 0 2
У -6 0
-9
Найдём абсциссы
точек пересечения
графиков
3 ОТВЕТ:
х=-2, х=1
-12
у=-3х²

24.

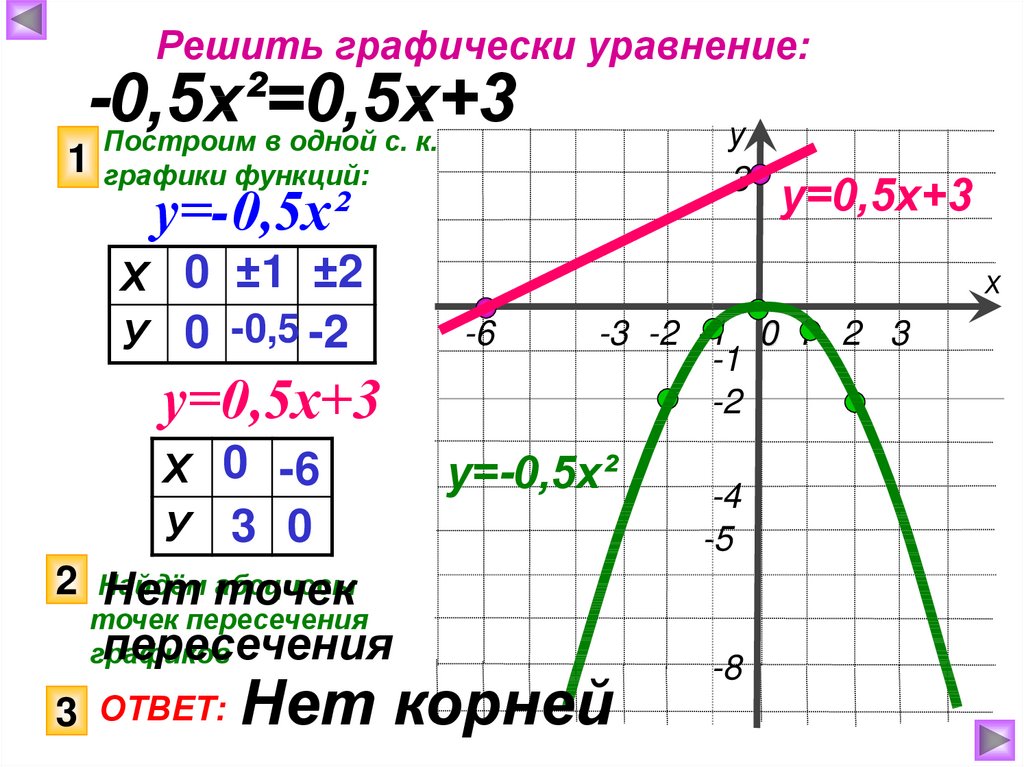
Решить графически уравнение:
-0,5х²=0,5х+3
Построим в одной с. к.
1
у
3
графики функций:
у=-0,5х²
Х 0 ±1 ±2
У 0 -0,5 -2
у=0,5х+3
Х 0 -6
У 3 0
х
-6
-3 -2 -1 0 1 2 3
-1
-2
у=-0,5х²
-4
-5
2 Найдём
абсциссы
Нет точек
точек пересечения
графиков
пересечения
3 ОТВЕТ:
у=0,5х+3
Нет корней
-8

25.

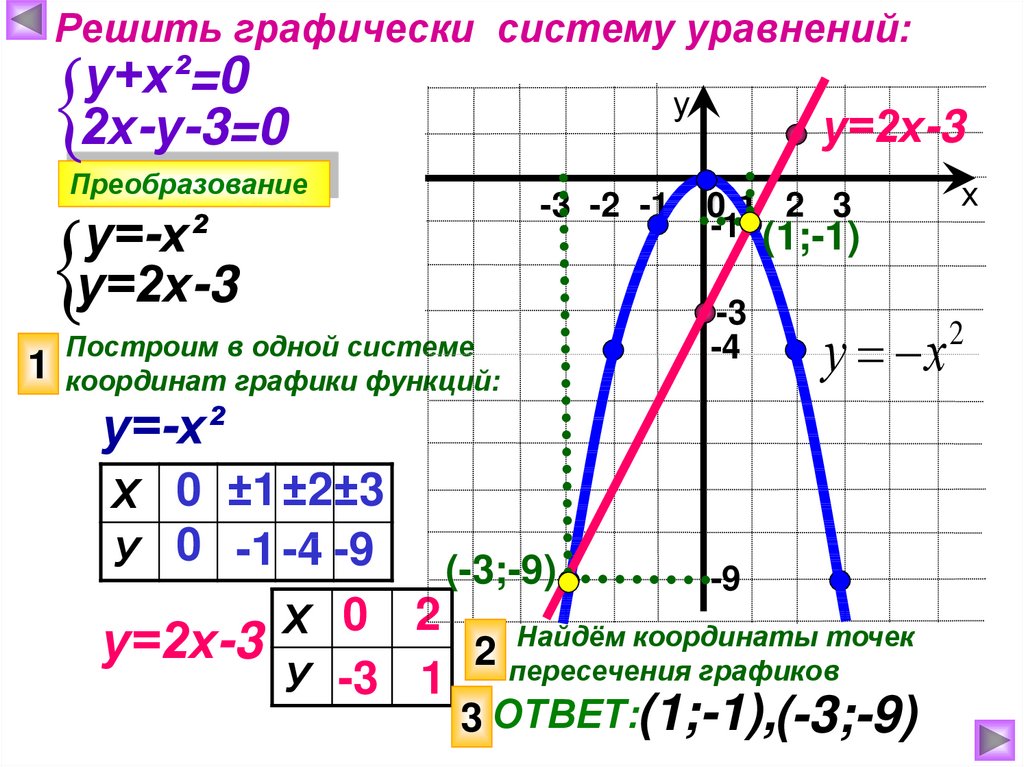
Решить графически систему уравнений:
у=-х²
у=2х-3
у+х²=0
2х-у-3=0
у
Преобразование
1
-3 -2 -1
Построим в одной системе
координат графики функций:
у=2х-3
01 2 3
-1 (1;-1)
-3
-4
у х
у=-х²
Х 0 ±1 ±2±3
У 0 -1 -4 -9
у=2х-3
(-3;-9)
-9
Х 0 2
Найдём координаты точек
2 пересечения
графиков
У -3 1
3 ОТВЕТ:(1;-1),(-3;-9)
х
2

26.

Постройте график функции
2х²,если -1≤х≤1
f(x)= 2,если 1<х≤6
и опишите её свойства.

27.

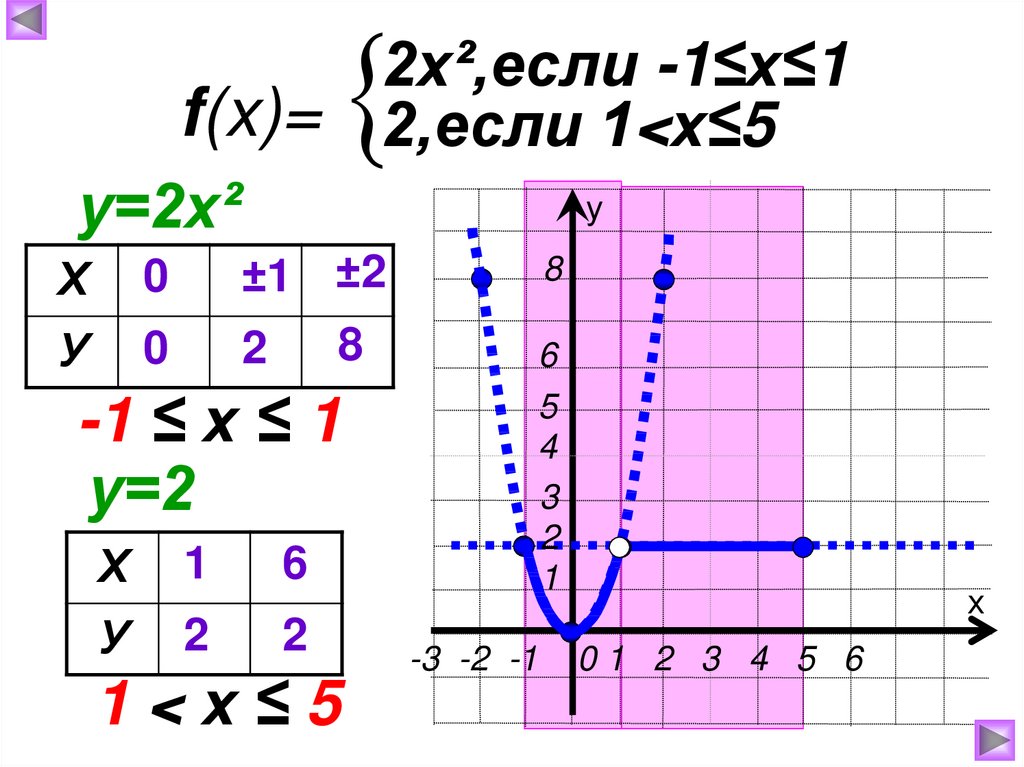
2х²,если -1≤х≤1
f(x)= 2,если 1<х≤5
у
у=2х²
Х
0
У
0
±1 ±2
8
2
8
6
5
4
3
2
1
-1 ≤ х ≤ 1
у=2
Х
1
6
У
2
2
1<х≤5
-3 -2 -1
х
01 2 3 4 5 6

28.

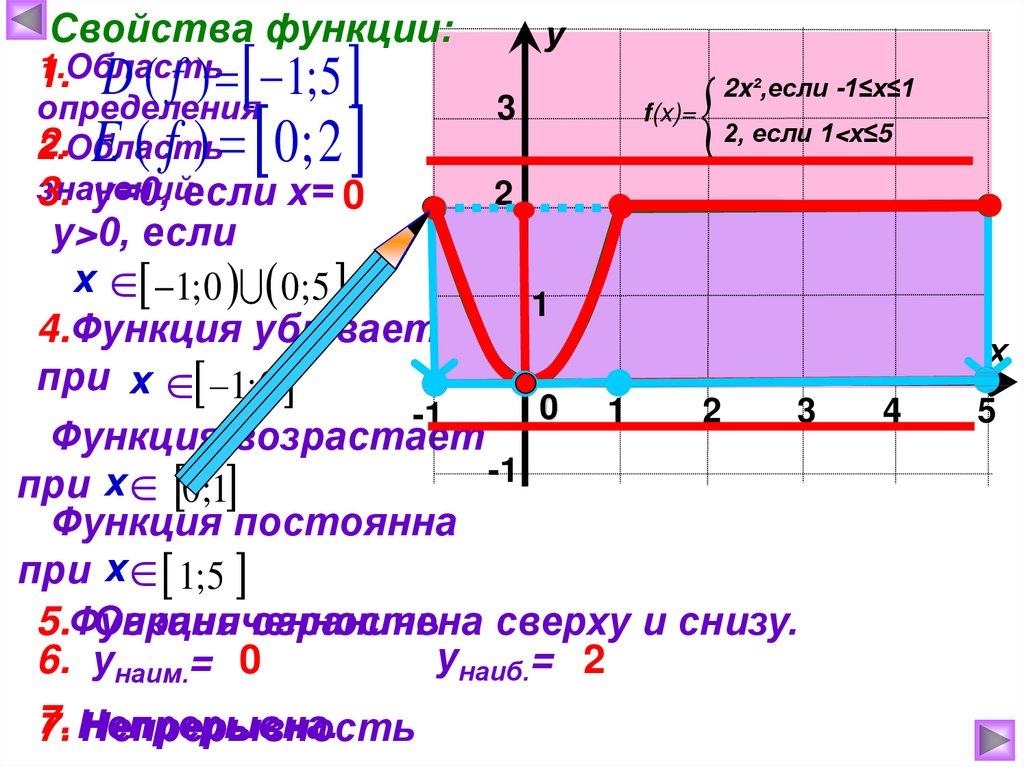
Свойства функции:
1.Область
1. D ( f ) 1; 5
определения
у
3
2x²,если -1≤х≤1
2, если 1<х≤5
2. E ( f ) 0 ; 2
2.Область
значений
2
3. у=0, если х= 0
у>0, если
х 1; 0 0; 5
1
4.Функция убывает
при х 1; 0
0 1
2
3
4
-1
Функция возрастает
-1
при х 0 ;1
Функция постоянна
при х 1; 5
5.Функция
Ограниченность
ограничена сверху и снизу.
унаиб.= 2
6. унаим.= 0
7. Непрерывна.
Непрерывность
f(x)=
х
5