Призма

1. Призма

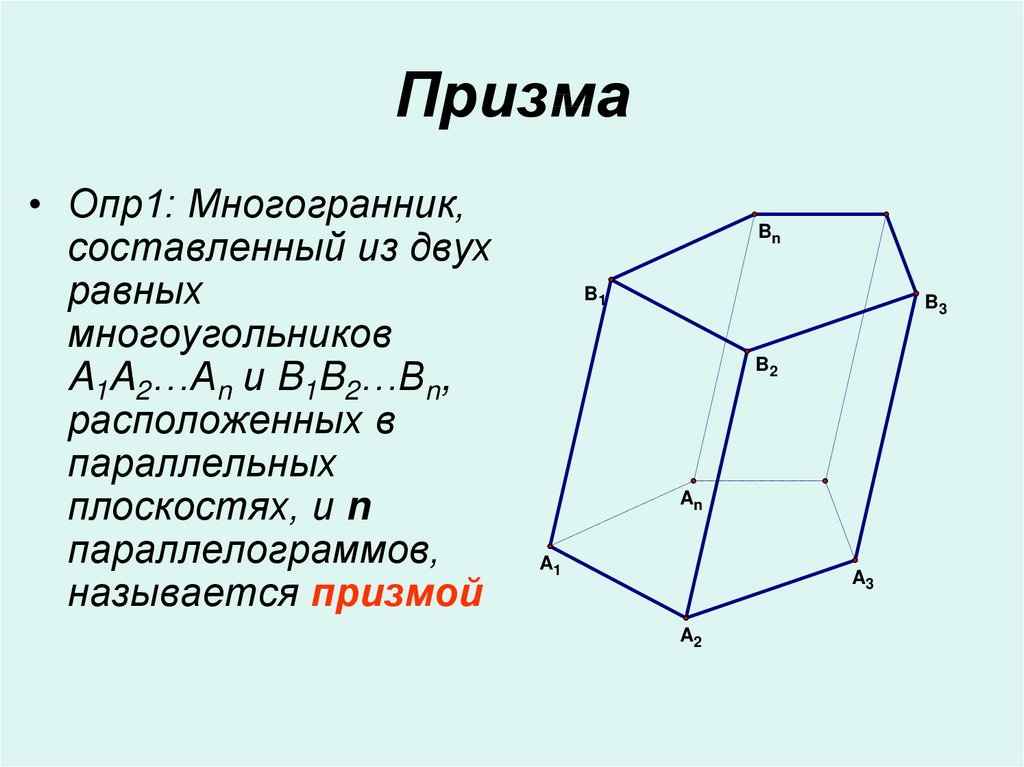
• Опр1: Многогранник,
составленный из двух
равных
многоугольников
A1A2…An и B1B2…Bn,
расположенных в
параллельных
плоскостях, и n
параллелограммов,
называется призмой
Bn
B1
B3
B2
An
A1
A3
A2

2.

Bn
B1
B3
B2
An
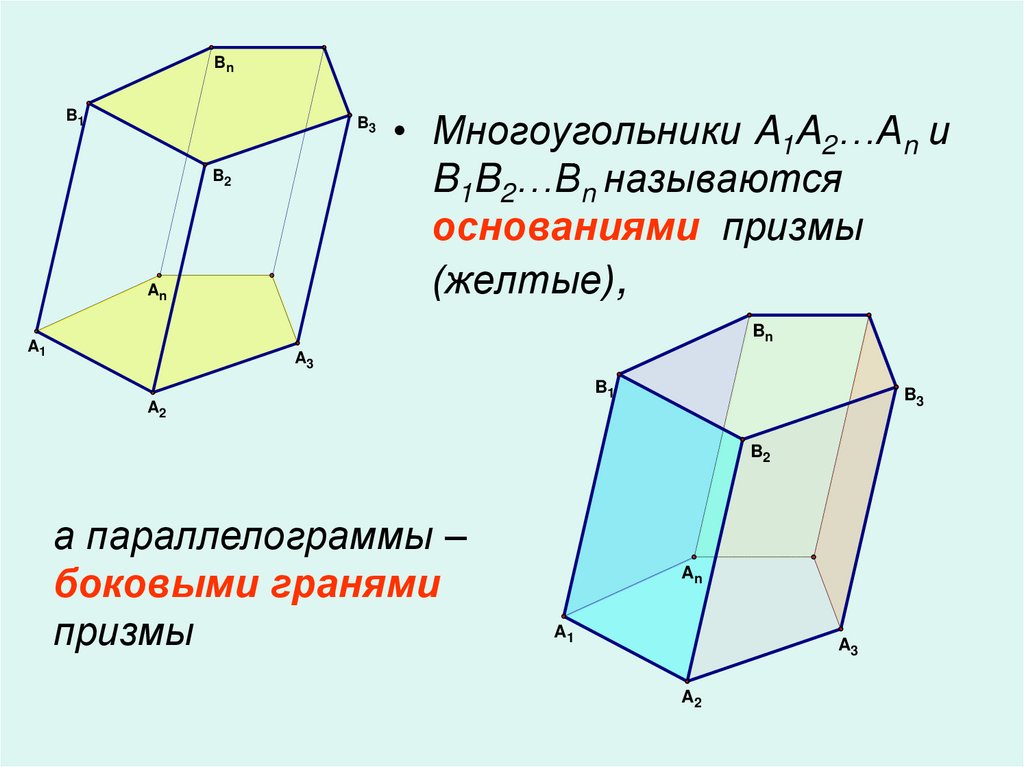
• Многоугольники A1A2…An и
B1B2…Bn называются
основаниями призмы
(желтые),
Bn
A1
A3
B1
B3
A2
B2
а параллелограммы –
боковыми гранями
призмы
An
A1
A3
A2

3.

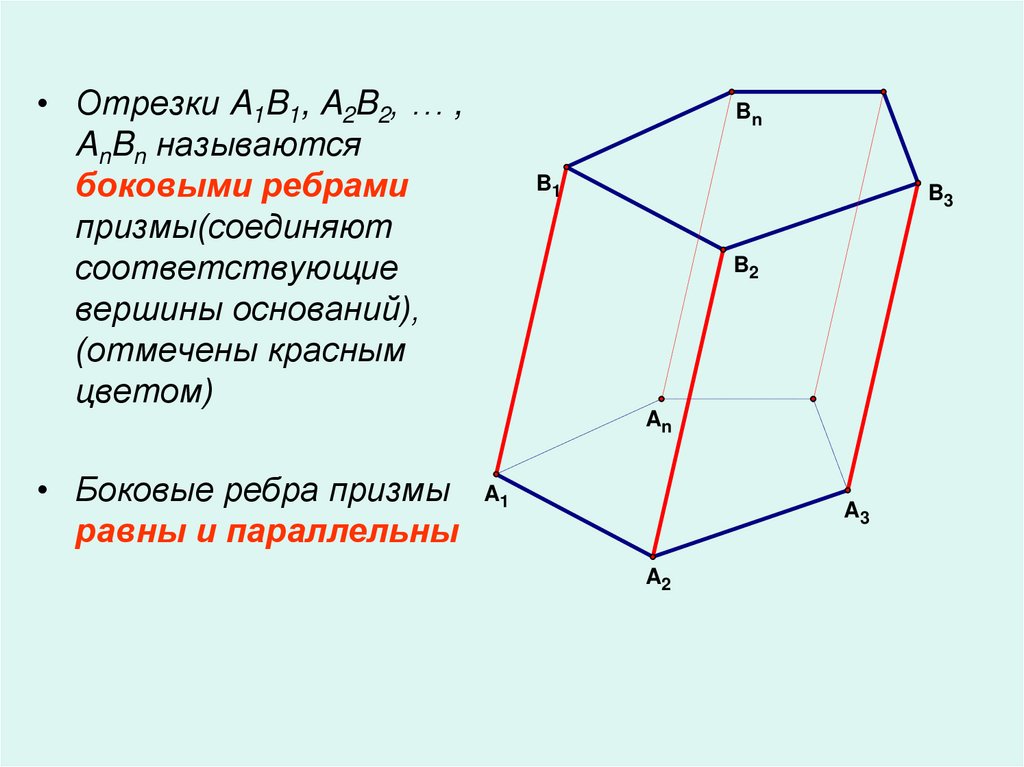
• Отрезки A1B1, A2B2, … ,
AnBn называются
боковыми ребрами
призмы(соединяют
соответствующие
вершины оснований),
(отмечены красным
цветом)
Bn
B1
B3
B2
An
• Боковые ребра призмы
равны и параллельны
A1
A3
A2

4.

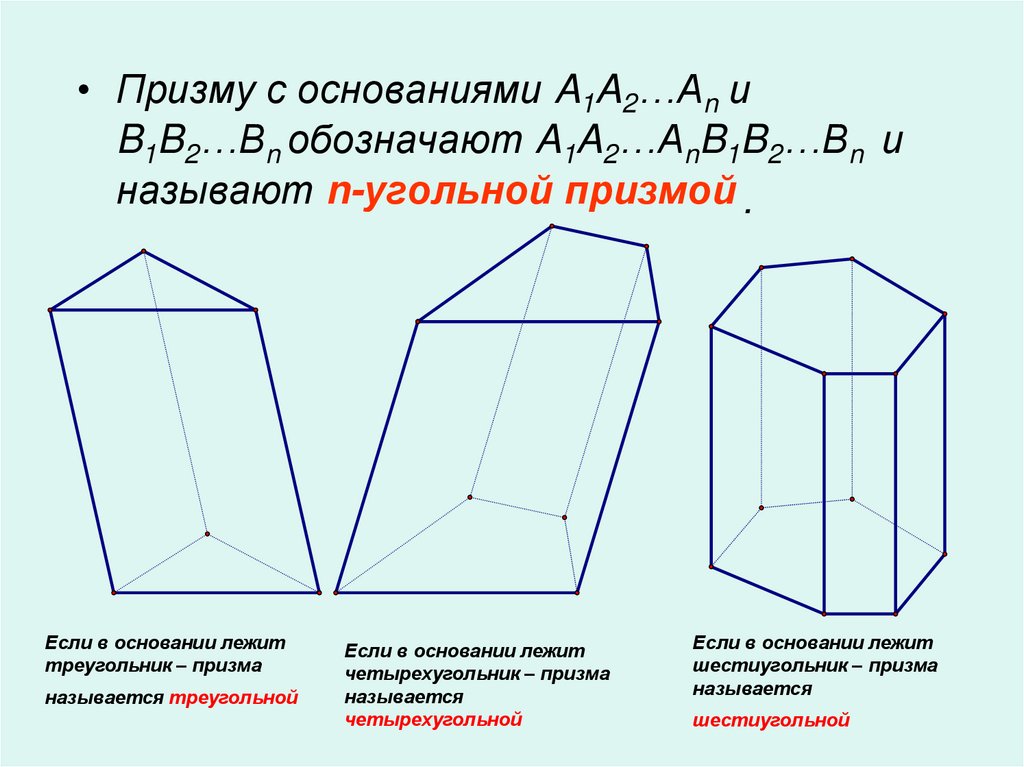
• Призму с основаниями A1A2…An и
B1B2…Bn обозначают A1A2…AnB1B2…Bn и
называют n-угольной призмой .
Если в основании лежит
треугольник – призма
называется треугольной
Если в основании лежит
четырехугольник – призма
называется
четырехугольной
Если в основании лежит
шестиугольник – призма
называется
шестиугольной

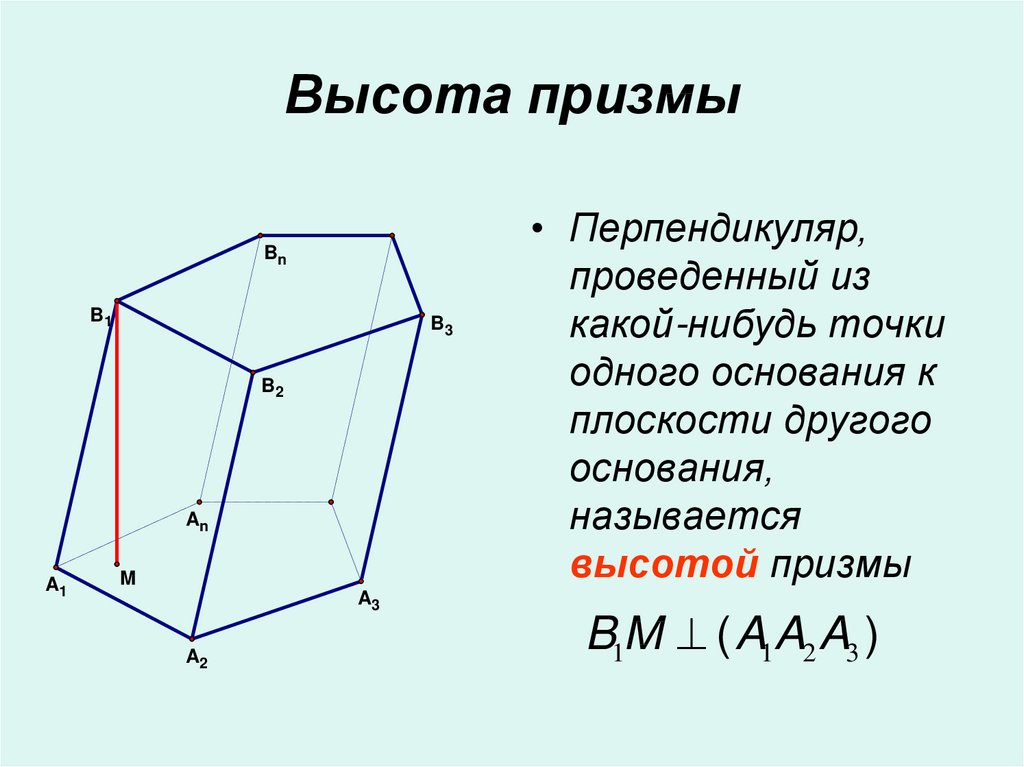
5. Высота призмы

Bn
B1
B3
B2
An
A1
M
A3
A2
• Перпендикуляр,
проведенный из
какой-нибудь точки
одного основания к
плоскости другого
основания,
называется
высотой призмы
B1M ( A1A2 A3 )

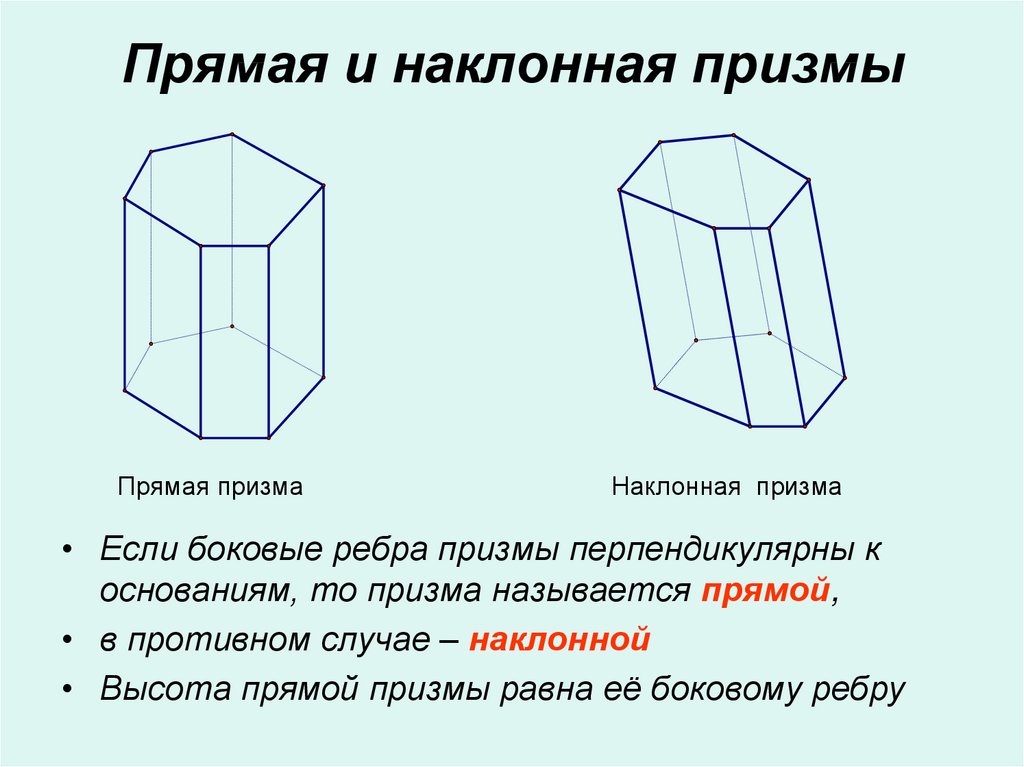
6. Прямая и наклонная призмы

Прямая призма
Наклонная призма
• Если боковые ребра призмы перпендикулярны к
основаниям, то призма называется прямой,
• в противном случае – наклонной
• Высота прямой призмы равна её боковому ребру

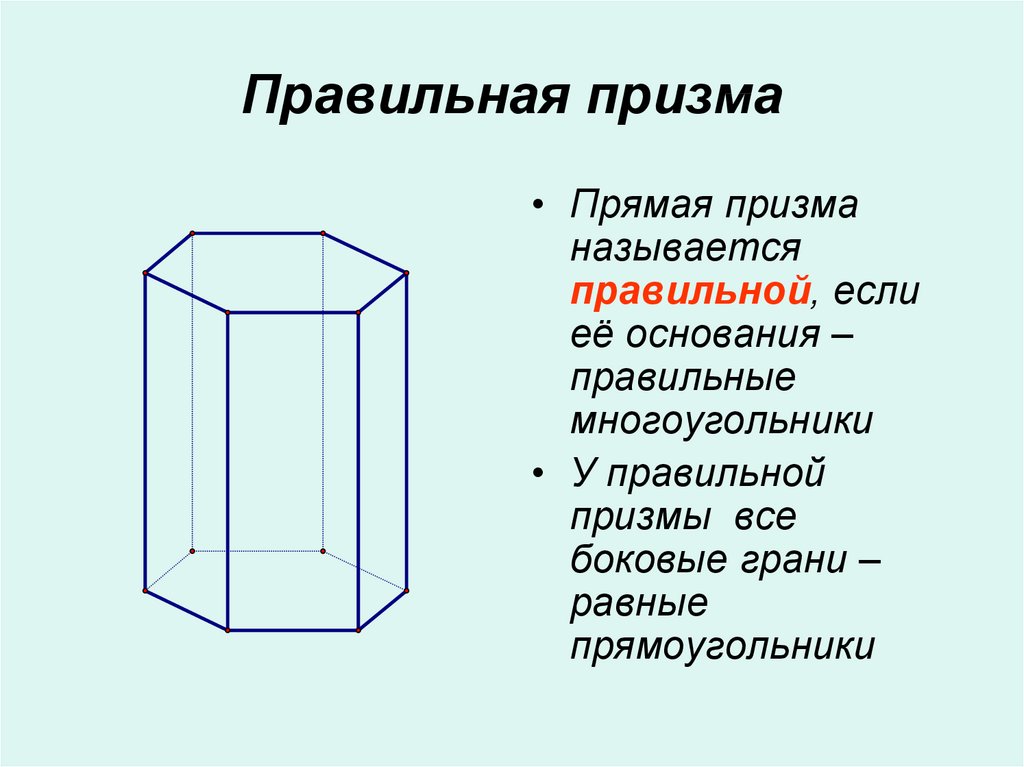
7. Правильная призма

• Прямая призма
называется
правильной, если
её основания –
правильные
многоугольники
• У правильной
призмы все
боковые грани –
равные
прямоугольники

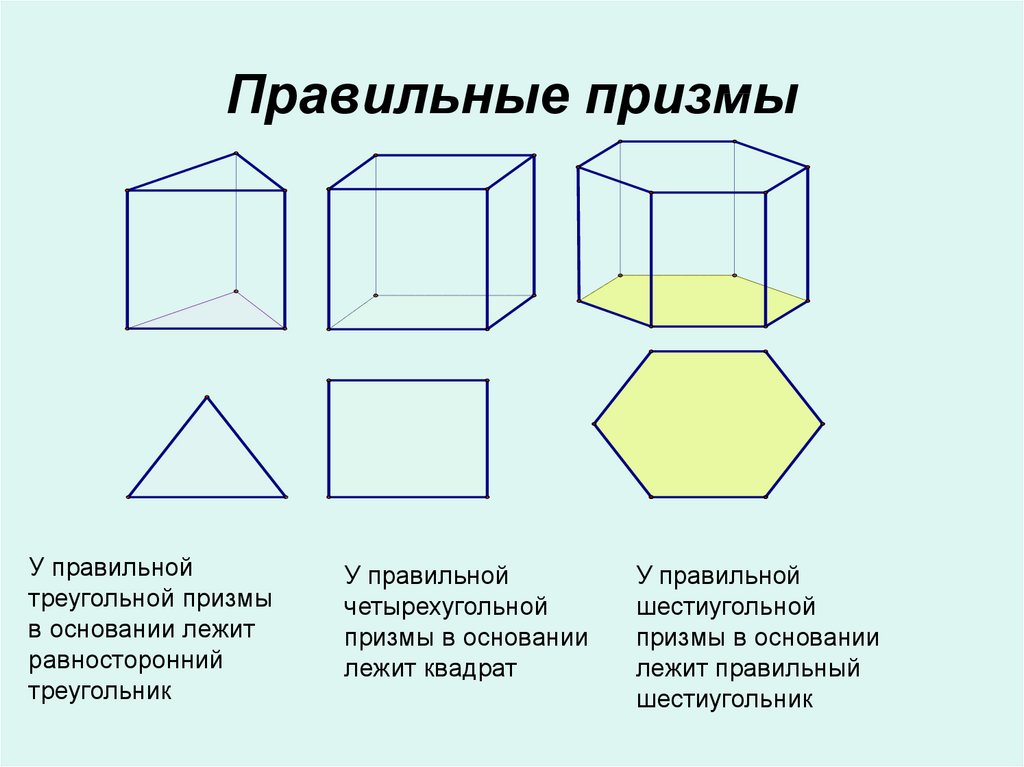
8. Правильные призмы

У правильной
треугольной призмы
в основании лежит
равносторонний
треугольник
У правильной
четырехугольной
призмы в основании
лежит квадрат
У правильной
шестиугольной
призмы в основании
лежит правильный
шестиугольник

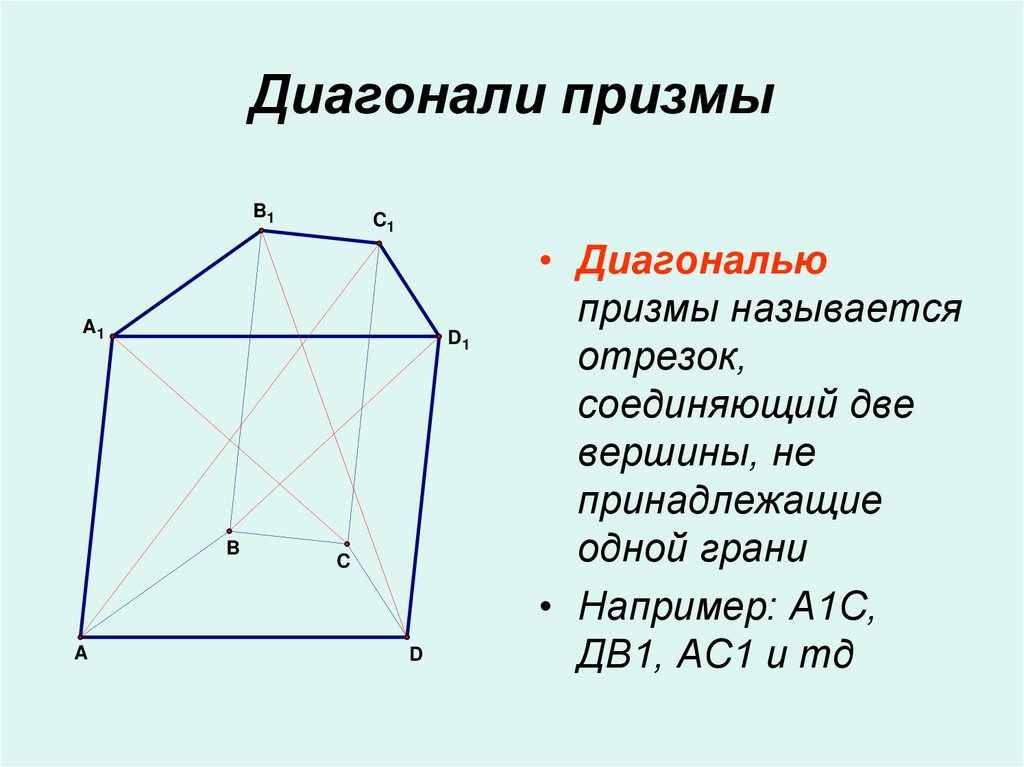
9. Диагонали призмы

B1
C1
A1
D1
B
A
C
D
• Диагональю
призмы называется
отрезок,
соединяющий две
вершины, не
принадлежащие
одной грани
• Например: А1С,
ДВ1, АС1 и тд

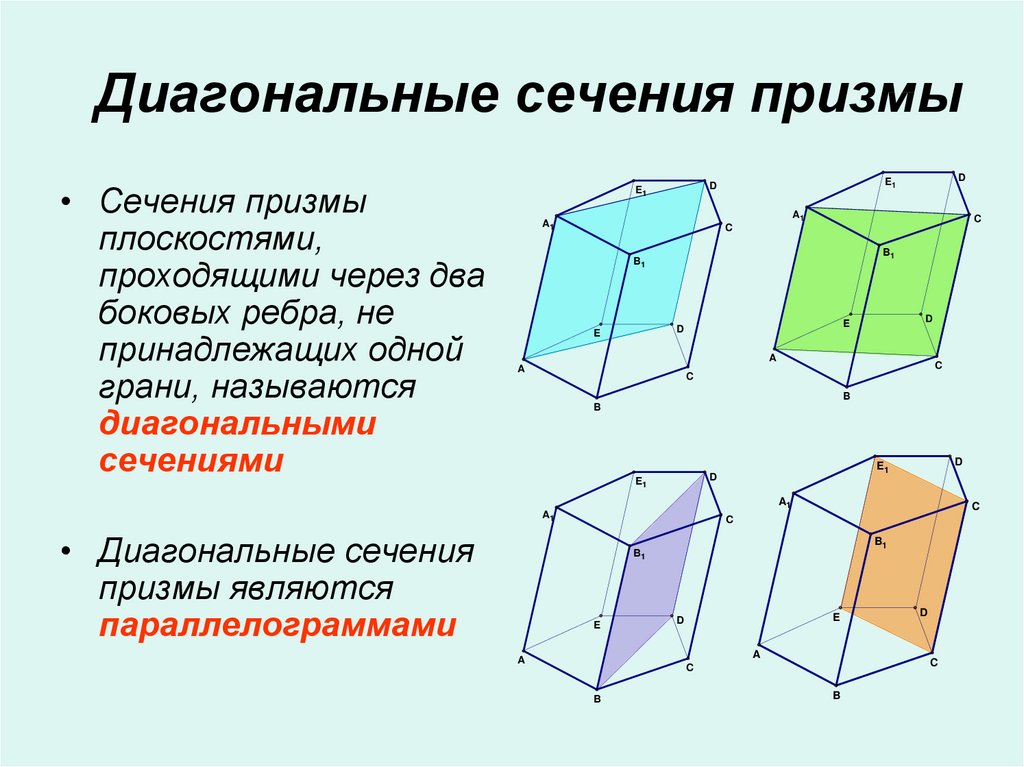
10. Диагональные сечения призмы

• Сечения призмы
плоскостями,
проходящими через два
боковых ребра, не
принадлежащих одной
грани, называются
диагональными
сечениями
D
E1
D
E1
A1
A1
C
C
B1
B1
D
E
D
E
A
A
C
C
B
B
E1
D
E1
D
A1
A1
• Диагональные сечения
призмы являются
параллелограммами
C
C
B1
B1
E
E
D
A
A
C
C
B
D
B