Similar presentations:
Дифференцирование функций
1. Повторение
Дифференцированиефункций
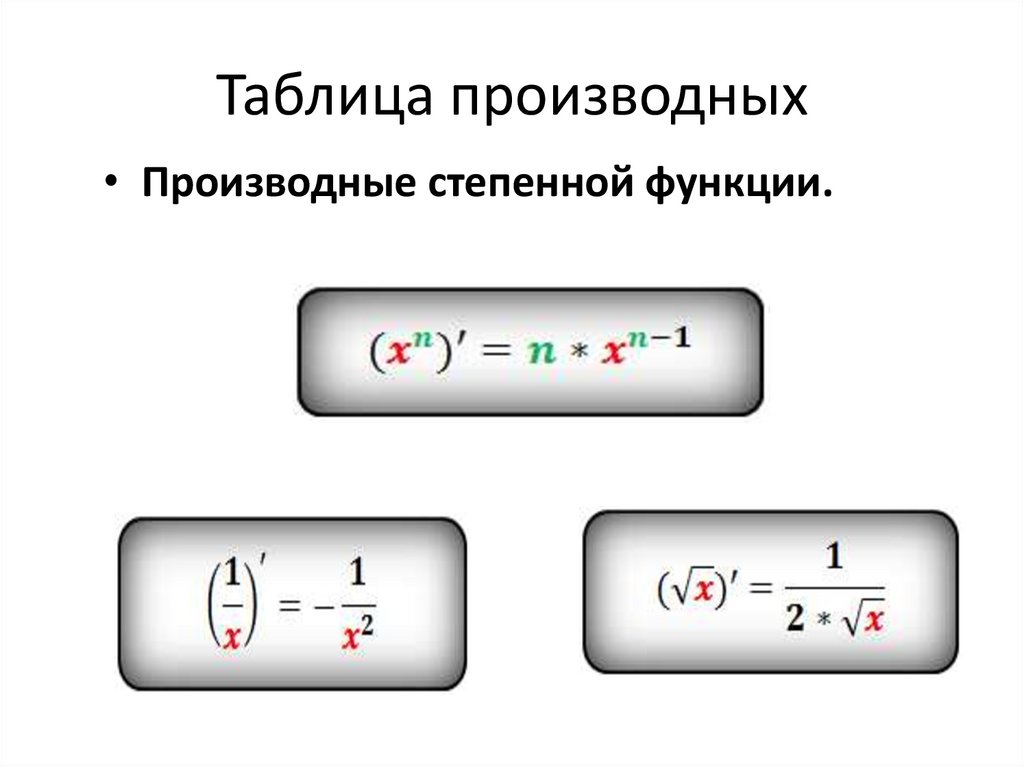
2. Таблица производных
• Производные степенной функции.3. Таблица производных
• Производные показательной функции.4. Таблица производных
• Производные логарифмической функции.5. Таблица производных
• Производные тригонометрическойфункции.
6. Таблица производных
• Производные обратнойтригонометрической функции.
7. Правила дифференцирования
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b)функции, С – постоянная.
(C ) 0
(u v ) u v
(u v ) u v u v (C u ) C u
(u v w ) u v w u v w u v w
u u v u v
C
C
v
2
2
v
v
v
v
8.
9. Производные высших порядков
Производная y f (x ) функции y f (x )есть также функция от x и называется
производной первого порядка.
Если функция f (x ) дифференцируема, то
ее производная называется производной
второго порядка и обозначается:
y ;
f ( x );
2
d y
2
dx
y ( y )
10.
Монотонностьи экстремумы
11.
Если, то
функция у= f(х)
возрастает .
!
f (х)≥0
Если
, то
функция у= f(х)
убывает .
!
f (х)≤0
12.
Внутренние точки области определенияфункции, в которых производная
функции равна нулю, называют
стационарными, а внутренние точки
области определения функции, в
которых функция непрерывна, но
производная не существует –
критическими.
13.
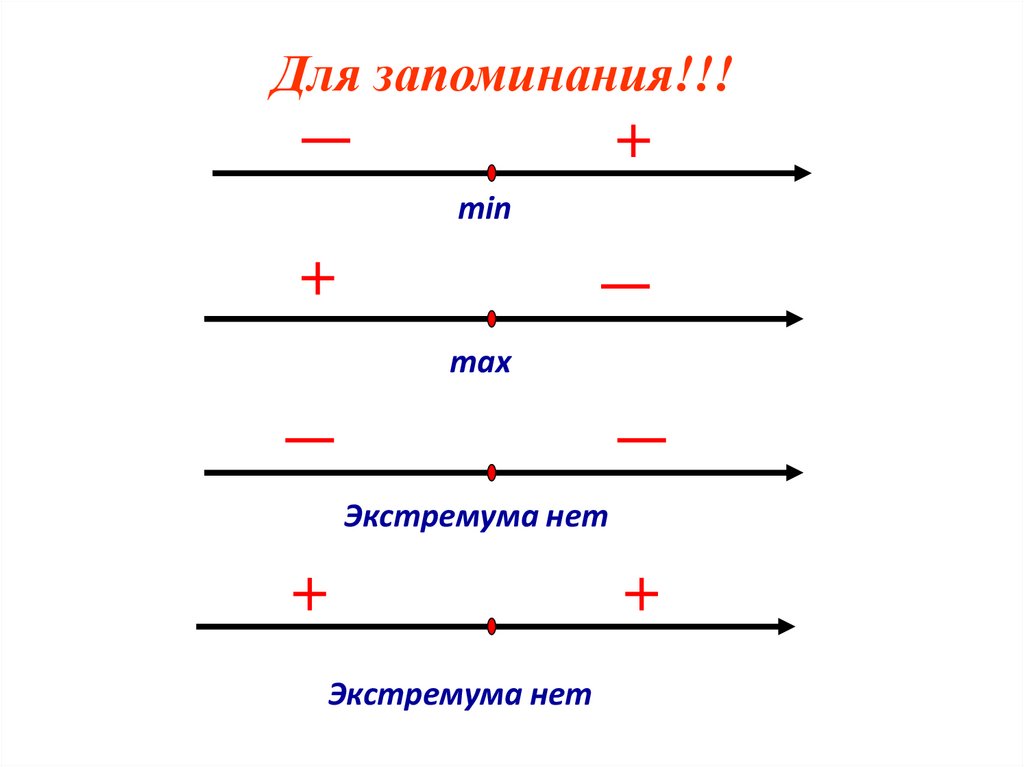
Для запоминания!!!min
max
Экстремума нет
Экстремума нет
14. Выпуклость и вогнутость функции
15.
Если вторая производнаяфункции у = f (х) на
данном интервале
положительна, то кривая
вогнута ,
а если отрицательна –
выпукла.
16.
Точки, в которых выпуклостьменяется на вогнутость или
наоборот,
называются точками перегиба
17.
График функцииГрафик функции
у = f (х) –
у = f (х) –
вогнутая кривая
выпуклая кривая
«+»
«-»









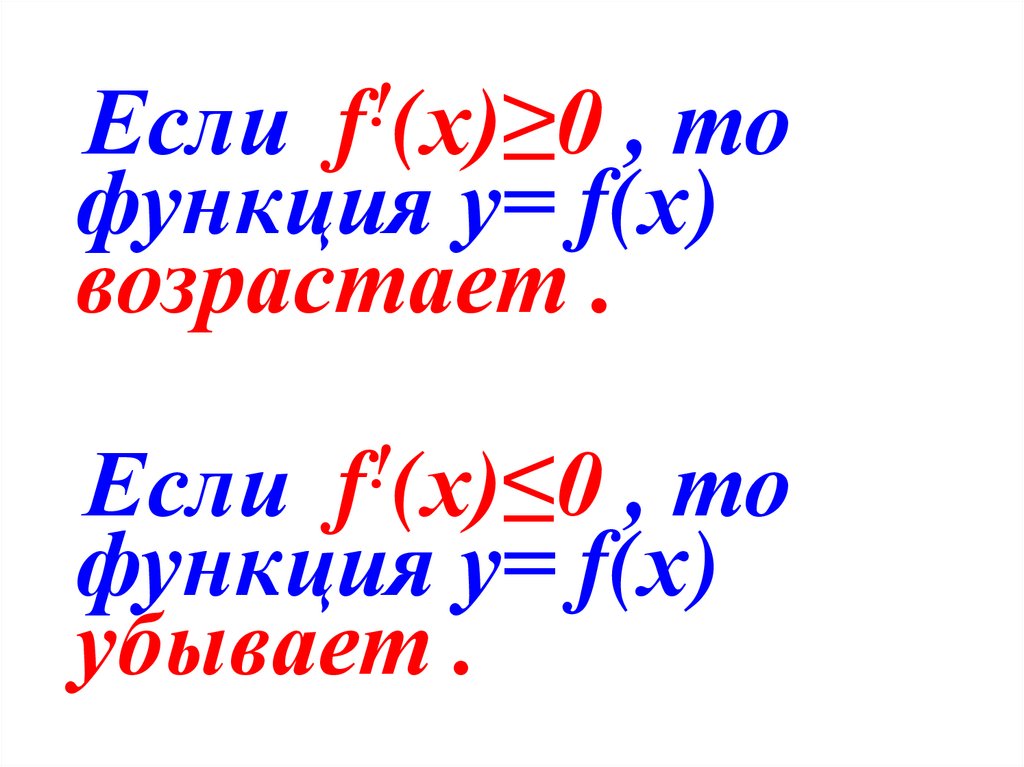





 mathematics
mathematics








