Similar presentations:
Динамика движения
1. ДИНАМИКА
2.
1. Наклонная плоскость, образующая угол = 30 с плоскостьюгоризонта, имеет длину l = 2 м. Тело, двигаясь равноускоренно,
соскользнуло с этой плоскости за время t = 2 с. Определить коэффициент трения тела о плоскость.
Дано:
= 30
l=2м
t=2с
Найти:
Решение:
Y
F тр
N
a
mg
Fрез m a
X
3.
YF тр
N
a
mg
X
N mg F тр m a
x : mgsin Fтр mа
y : N mgcos 0
4.
mgsin Fтр mаN mgcos
Fтр N
mgsin Fтр mа
Fтр mgcos
mgsin mgcos mа
gsin gcos а
5.
gsin gcos аgsin a
gcos
a
tg
gcos
ax t
x x0 υ0 x t
2
2
at
l
2
2
6.
2at
l
2
2l
a 2
t
2 2
2
a 2 1м/с
2
a
tg
gcos
1
tg 30
0 ,46
10 cos30
7.
2. Автомобиль массой m = 5 т движется со скоростью = 10 м/с повыпуклому мосту. Определить силу давления автомобиля на мост в
его верхней части, если радиус кривизны моста R = 50 м.
Дано:
m=5т
= 10 м/с
R = 50 м
Найти:
F.
Си:
5 103 кг
Решение:
N
F
Fрез m a
N mg m an
N m g m an
an
mg
8.
N m g m anN m ( g an )
N F - 3 закон Ньютона
N F
F m ( g an )
2
υ
аn
R
2
υ
F m (g )
R
9.
2υ
F m (g )
R
2
10
F 5 103 (10
) 40 103 40кН
50
10.
3. Материальная точка массой m = 2 кг движется под действием2
3
некоторой силы F согласно уравнению x A Bt Ct Dt ,
С = 1 м/с2, D = -0,2 м/с3. Найти значение этой силы в момент
времени t = 2 с. В какой момент времени сила равна нулю?
Дано:
m = 2 кг
С = 1 м/с2
D = -0,2 м/с3
t=2с
Найти:
F = f (t);
F(t) = 0
Решение:
x A Bt Ct 2 Dt 3
dx
2
υx
B 2C t 3D t
dt
dυx
ax
2C 6 D t
dt
11.
ax 2C 6D tF m ax
F (t ) m (2C 6 Dt )
F (2) 2 (2 1 6 0,2 2) -0,8 H
F (t ) m (2C 6 Dt ) 0
2C
C
t
6D
3D
12.
2CC
t
6D
3D
1
t
1,7c
3 ( 0,2)
13.
4. Мотоциклист в цирке едет вдоль внутренней поверхностивертикального цилиндра радиусом R = 15 м. Центр масс мотоцикла
с человеком отстоит на а = 1 м от места соприкосновения колёс со
стенкой. Коэффициент трения шин о стенки = 0,5. Определить:
1) минимальную скорость с которой должен ехать мотоциклист;
2) угол наклона мотоциклиста к горизонтальной поверхности.
Дано:
R = 15 м
а=1м
= 0,5
Найти:
1) min;
2) .
Решение:
1
an
N
F тр
Fрез m a
mg
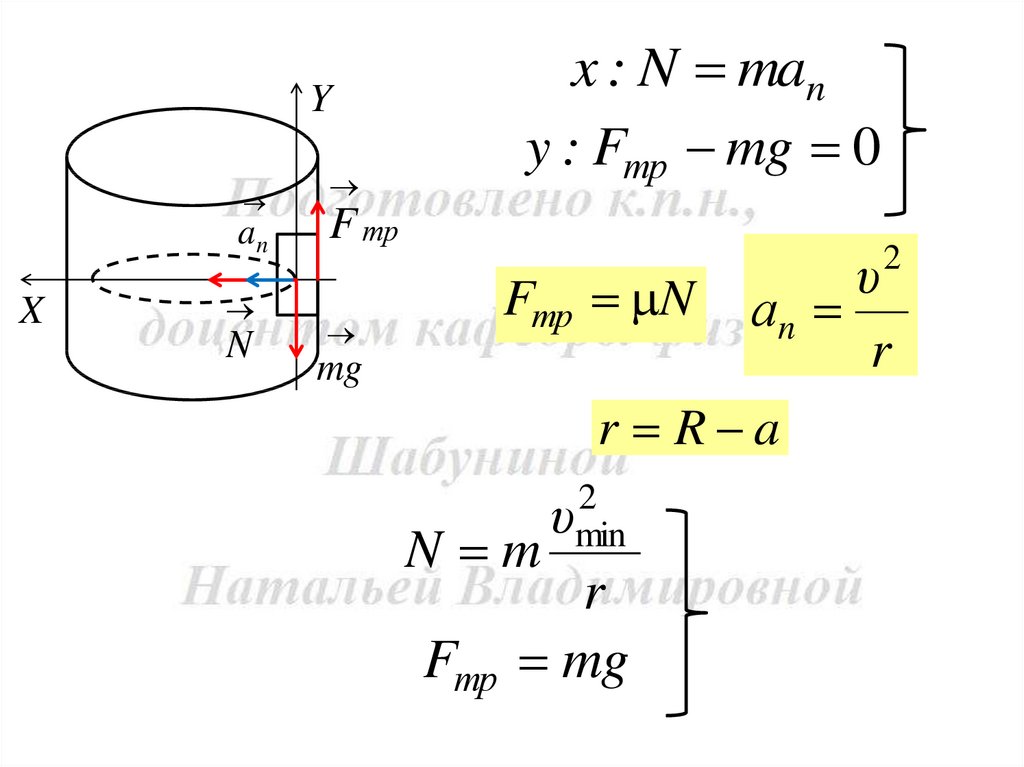
N mg F тр m a
14.
x : N many : Fтр mg 0
Y
an
X
N
F тр
2
Fтр
mg
N m
Fтр
υ
N аn
r
r R a
2
υmin
r
mg
15.
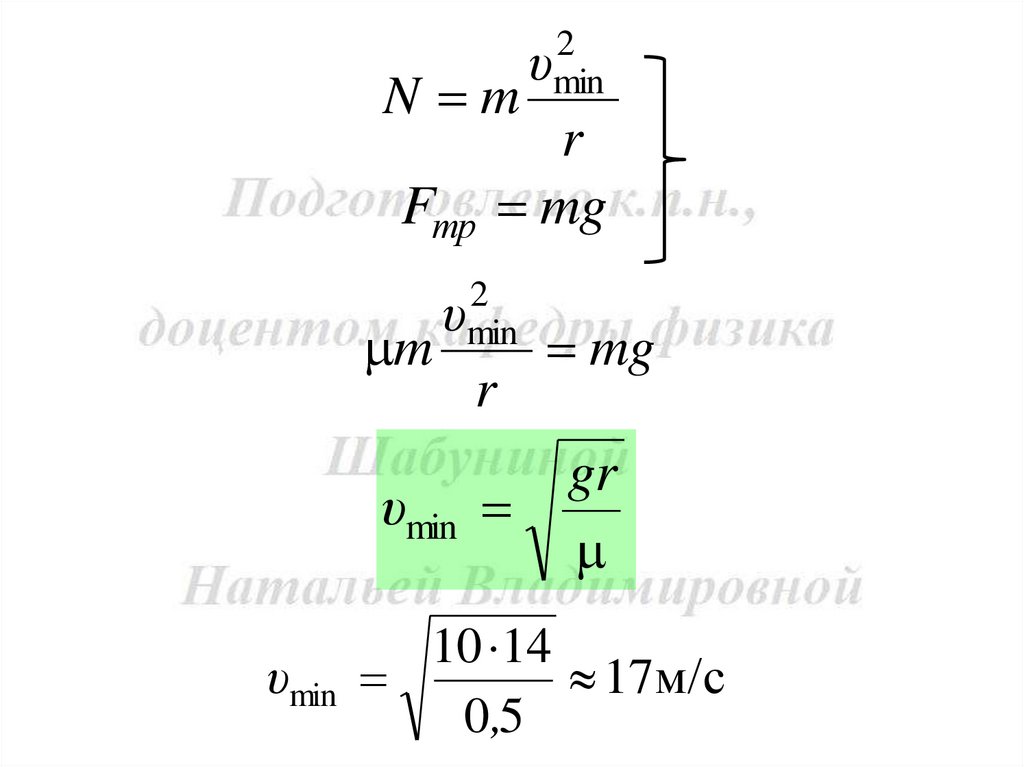
N mr
mg
Fтр
m
2
υmin
υmin
υmin
2
υmin
r
mg
gr
10 14
17м/с
0,5
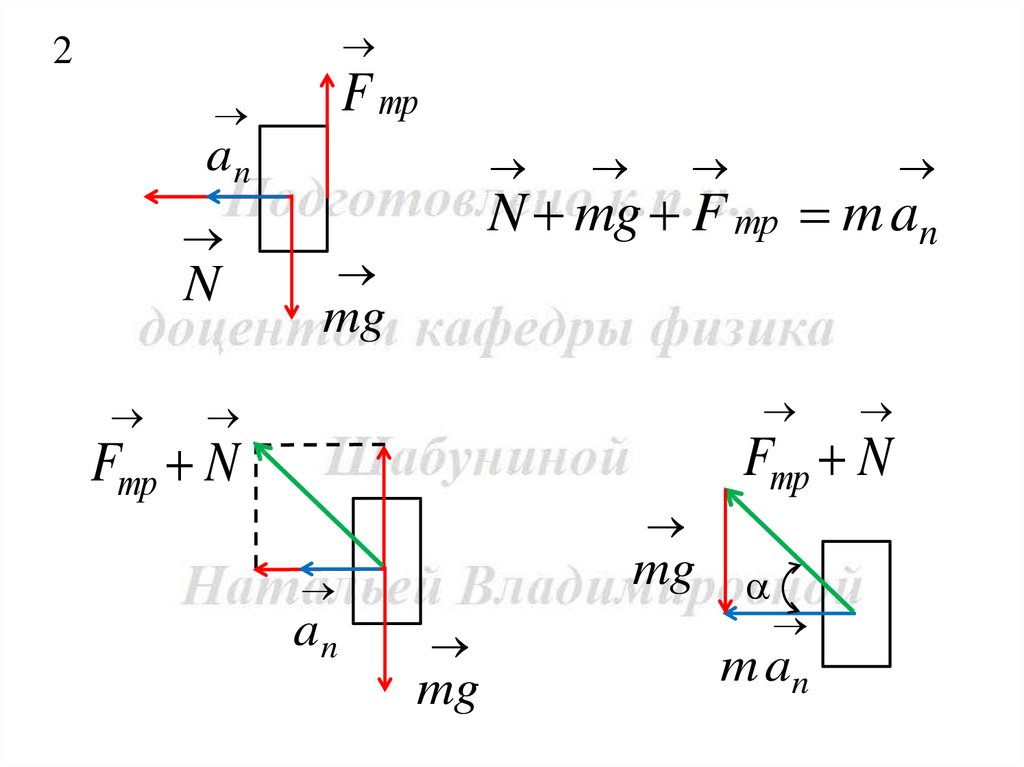
16.
2F тр
an
N
N mg F тр m an
mg
Fтр N
Fтр N
mg
an
mg
m an
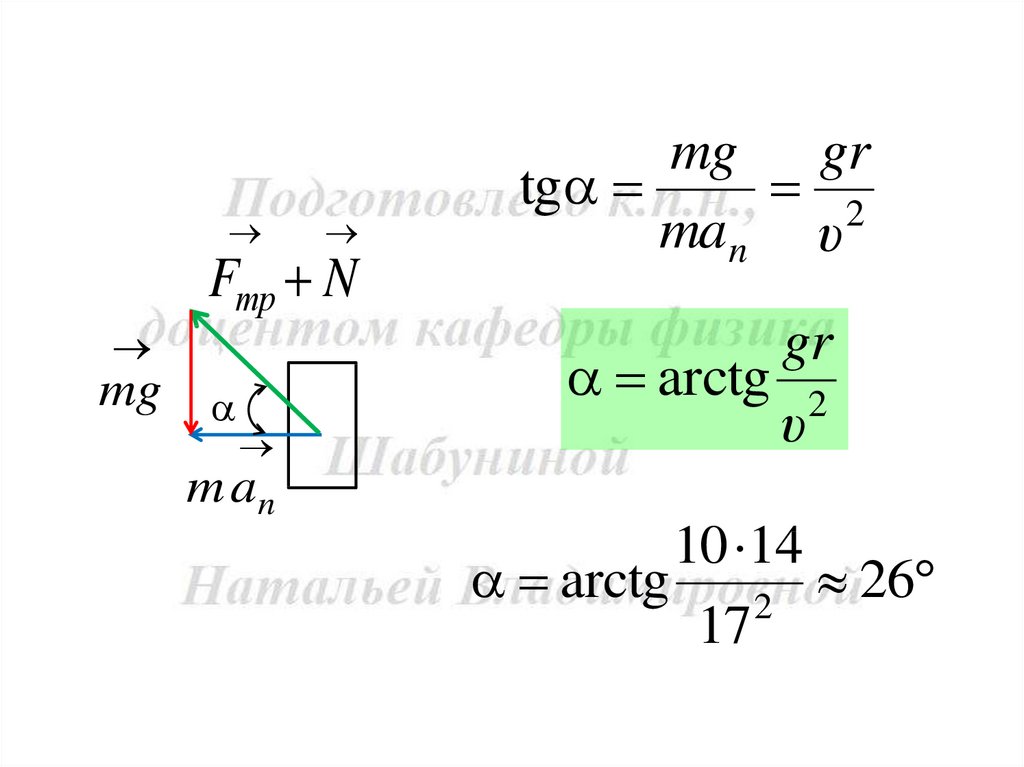
17.
Fтр Nmg
m an
mg gr
tg
2
man υ
gr
arctg 2
υ
10 14
arctg
26
2
17
18.
5. Парашютист масса которого m = 80 кг, совершает затяжнойпрыжок. Считая, что сила сопротивления воздуха пропорциональна
скорости, определить, через какой промежуток времени скорость
движения парашютиста будет равна 0,9 от скорости установившегося движения. Коэффициент сопротивления k = 10 кг/с. Начальная скорость парашютиста равна нулю.
Дано:
m = 80 кг
= 0,9 уст
k = 10 кг/с
0 = 0 м/с
Найти:
.
Fc
υ
Решение:
Fc k υ
Fрез
mg
m dυ
dt
m dυ
m g Fc
dt
19.
m dυm g Fc
dt
mdυ
mg Fc
dt
mdυ
mg kυ
dt
dυ
dt
mg kυ m
Fc
υ
Y
mg
0 ,9υ уст
0
dυ
1
dt
mg kυ m 0
20.
0 ,9υ уст0
dυ
1
dt
mg kυ m 0
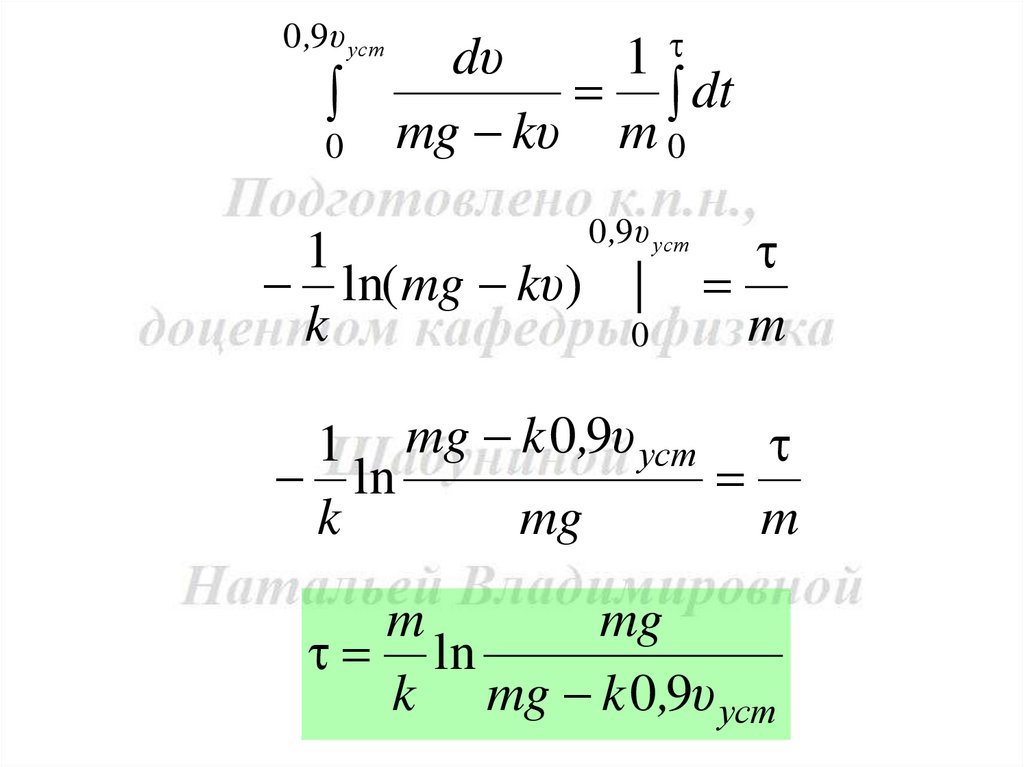
0 ,9υ уст
1
ln( mg kυ) |
k
0
m
1 mg k 0,9υ уст
ln
k
mg
m
m
mg
ln
k mg k 0,9υ уст
21.
mmg
ln
k mg k 0,9υ уст
mdυ
mg kυ
dt
mg kυ уст 0
υ уст
υ уст
mg
k
80 10
80м/с
10
22.
mmg
ln
k mg k 0,9υ уст
80
80 10
ln
18с
10 80 10 10 0,9 80
23.
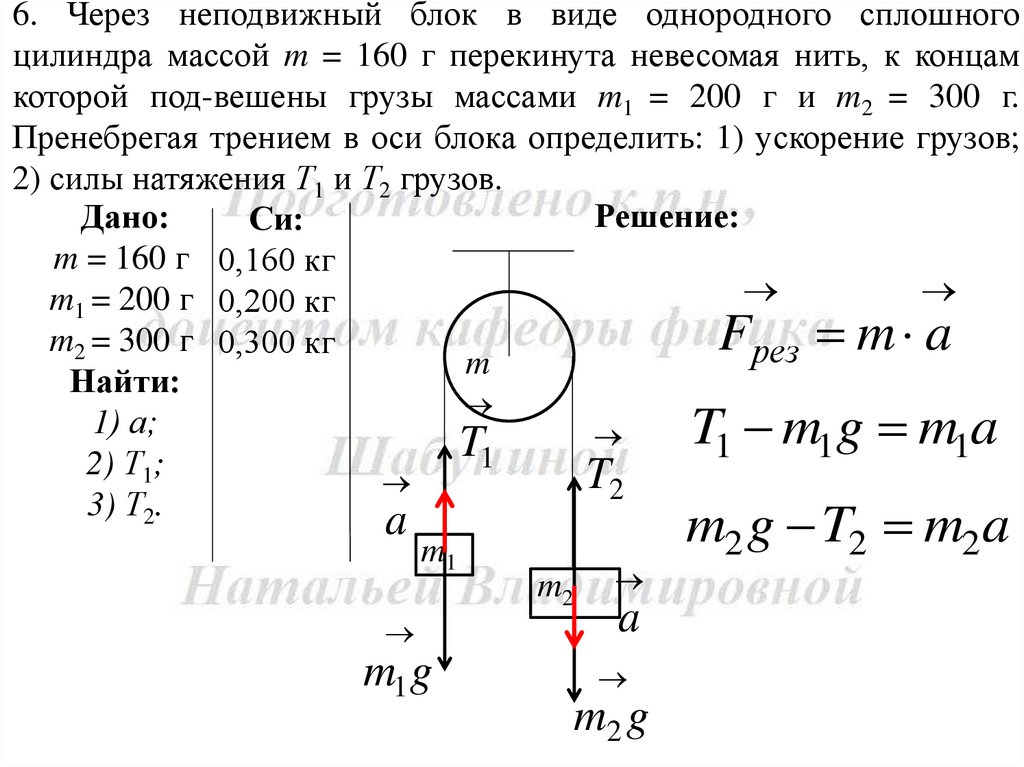
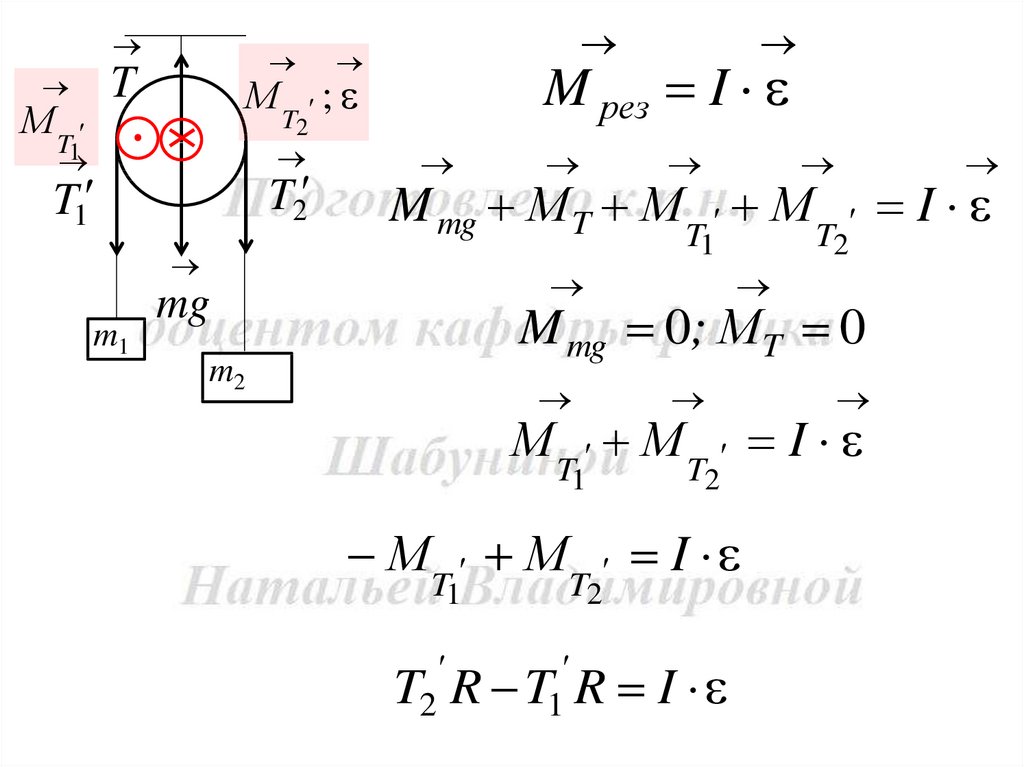
6. Через неподвижный блок в виде однородного сплошногоцилиндра массой m = 160 г перекинута невесомая нить, к концам
которой под-вешены грузы массами m1 = 200 г и m2 = 300 г.
Пренебрегая трением в оси блока определить: 1) ускорение грузов;
2) силы натяжения Т1 и Т2 грузов.
Решение:
Дано:
Си:
m = 160 г 0,160 кг
m1 = 200 г 0,200 кг
F
m
a
m2 = 300 г 0,300 кг
рез
m
Найти:
1) а;
T
m
g
m
a
T
1
1
1
1
2) Т1;
T2
3) Т2.
a
m2 g T2 m2 a
m1
m2
m1 g
a
m2 g
24.
TМT
M рез I
МT ;
2
1
T2
T1
M mg М T М T М T I
1
m1
mg
2
M mg 0; М T 0
m2
МT МT I
1
2
МT МT I
1
2
T2 R T1 R
I
25.
T2 R T1 RI
T1 T1
T2 T2
- 3 закон Ньютона
a R
a
T2 R T1 R I
R
26.
aT2 R T1 R I
R
T1 m1 g m1a
m2 g T2 m2 a
mR
I
2
2
2
mR a
(m2 g m2 a) R (m1 g m1a) R
2 R
ma
m2 g m2 a m1 g m1a
2
27.
mam2 g m2 a m1 g m1a
2
(m2 m1 ) g
a
m1 m2 m/ 2
(0,300 0,200) 10
2
a
1,7м/с
0,300 0,200 0,160/ 2
T1 m1 (a g )
T2 m2 (g - a)
28.
T1 m1 (a g )T2 m2 (g - a)
T1 0,200 (1,7 10) 2,3H
T2 0,300 (10 -1,7) 2,5H
29.
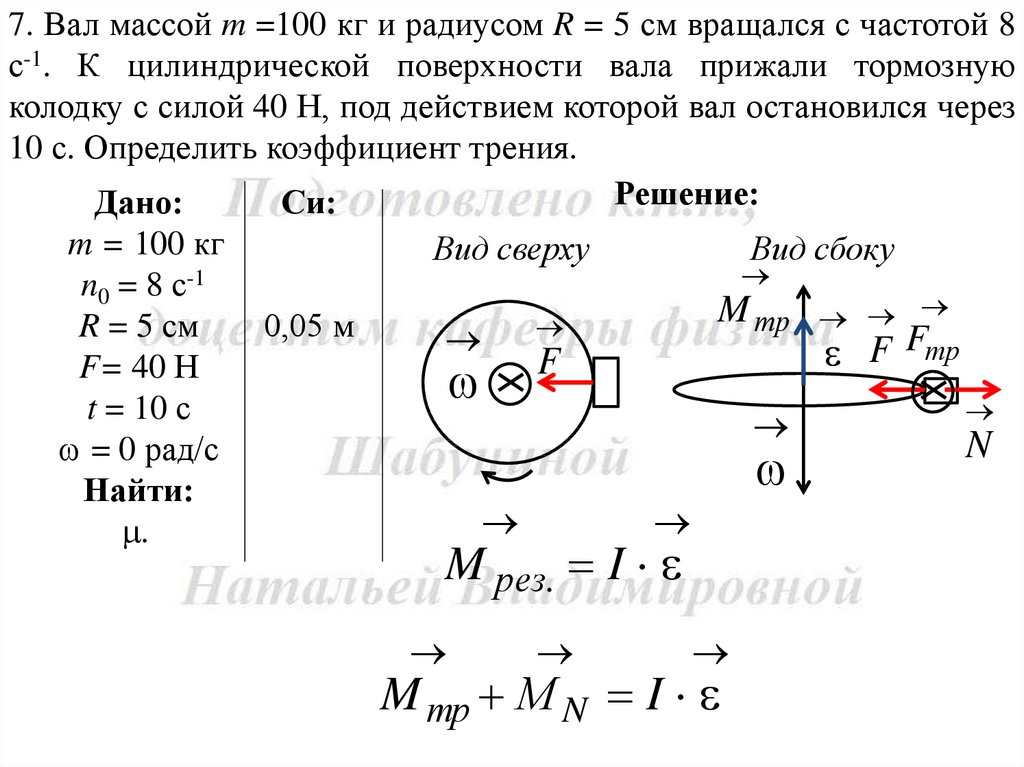
7. Вал массой m =100 кг и радиусом R = 5 см вращался с частотой 8с-1. К цилиндрической поверхности вала прижали тормозную
колодку с силой 40 Н, под действием которой вал остановился через
10 с. Определить коэффициент трения.
Решение:
Дано:
Си:
m = 100 кг
Вид сверху
Вид сбоку
n0 = 8 с-1
M
тр
R = 5 см
0,05 м
Fтр
F
F
F= 40 Н
t = 10 с
N
= 0 рад/с
Найти:
.
M рез. I
M тр М N I
30.
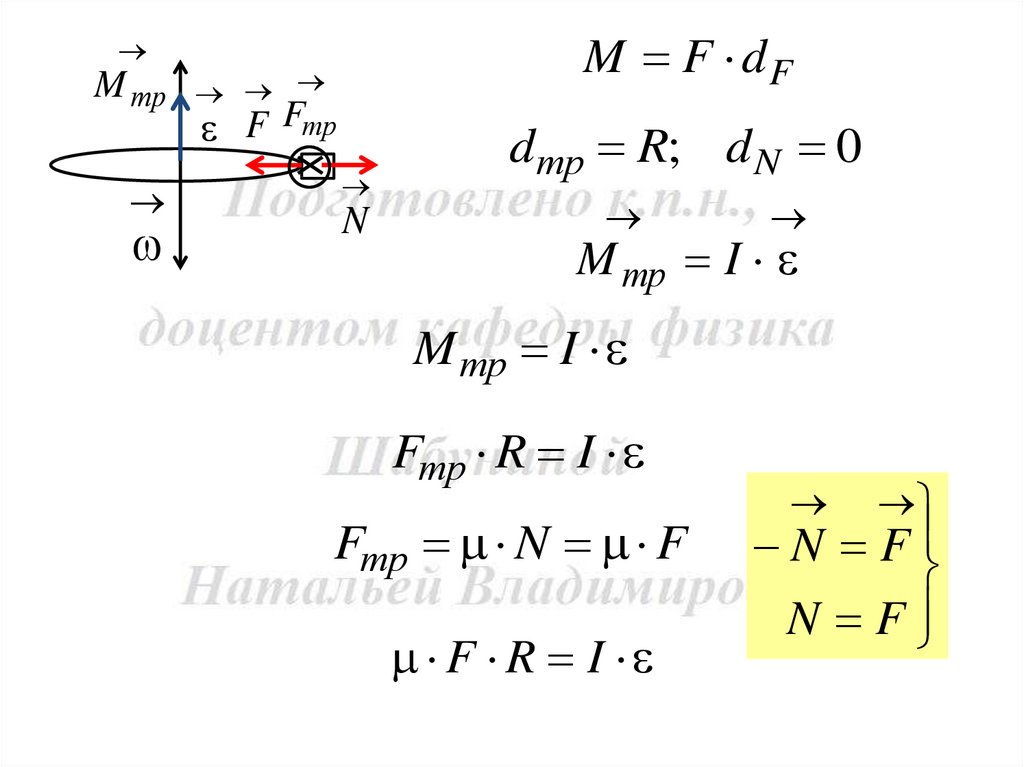
M трM F dF
F Fтр
N
dтр R; d N 0
M тр I
M тр I
Fтр R I
Fтр N F
F R I
N F
N F
31.
F R Im R
I
2
0
0
2 n0
t
t
t
2
m R 2 n0
F R
2
t
2
m R 2 n0
2 t F
2 n
32.
m R 2 n02 t F
100 0,05 2 3,14 8
0,314
2 10 40
33.
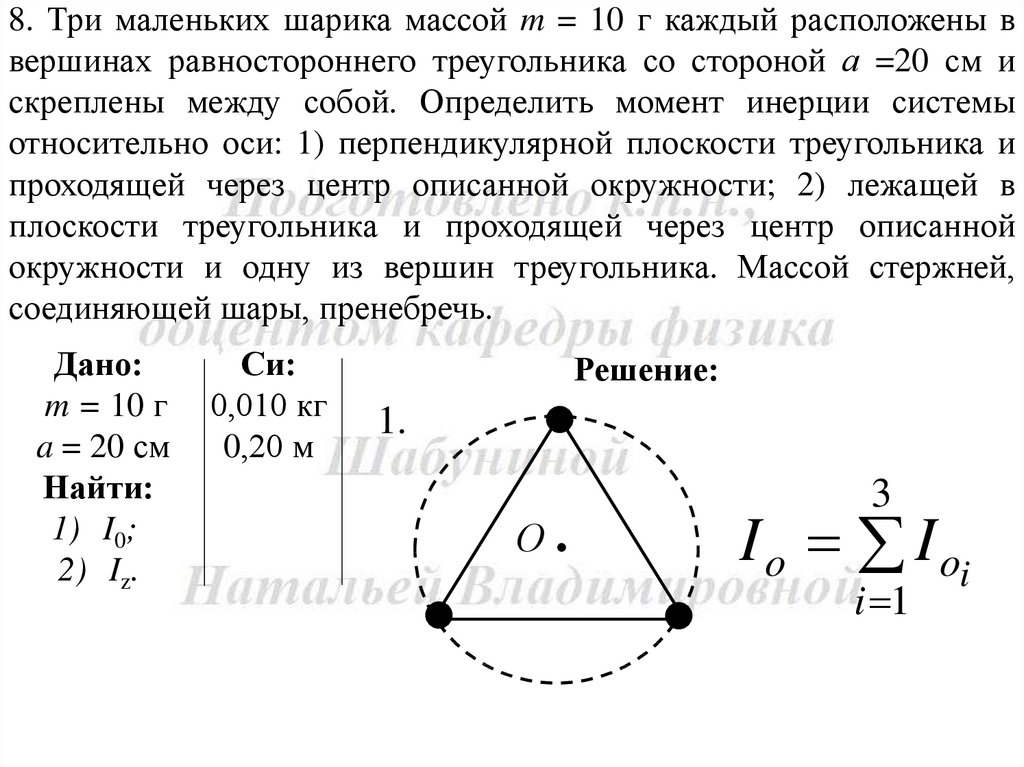
8. Три маленьких шарика массой m = 10 г каждый расположены ввершинах равностороннего треугольника со стороной а =20 см и
скреплены между собой. Определить момент инерции системы
относительно оси: 1) перпендикулярной плоскости треугольника и
проходящей через центр описанной окружности; 2) лежащей в
плоскости треугольника и проходящей через центр описанной
окружности и одну из вершин треугольника. Массой стержней,
соединяющей шары, пренебречь.
Дано:
m = 10 г
a = 20 см
Найти:
1) I0;
2) Iz.
Си:
0,010 кг
0,20 м
Решение:
1.
О.
3
I o I oi
i 1
34.
33
i 1
i 1
I o I oi mi ri
О.
r
2
3mr
a
r
3
2
I o ma
2
4
I o 0,010 0,20 4 10 кг м
2
2
35.
z2.
3
2
i 1
i 1
I z I zi mi ri
.
2mr
a
r
2
r
ma
Iz
2
4
2
I z 2 10 кг м
2
2
2
36.
9. Найти момент инерции тонкого однородного кольца радиусомR = 20 см и массой m = 100 г относительно оси, лежащей в
плоскости кольца и проходящей через его центр.
Дано:
m = 100 г
R = 20 см
Найти:
I0.
Си:
0,100 кг
0,20 м
Решение:
О
r
d
I o dm R
V
2
dm, dl
37.
Оr
d
I o dmr
dm, dl
2
V
r R cos
m m dm
l 2 R dl
dm dl
I o dlR cos Rd R cos
2
2
2
2
2
R cos ddl Rd
R cos d
3
2
3
0
2
38.
2I o R cos d
3
2
0
1
1
cos d sin 2
2
4
2
2
1
1
3
I o R sin2 |
4
2
0
3 1
1
1
1
R 2 sin 4 0 sin0
4
4
2
2
39.
3 11
1
1
R 2 sin 4 0 sin0
4
4
2
2
mR mR
R
2 R
2
3
3
m mR
I o
2 R 2
2
2
0,100 0 ,20
3
2
Io
2 10 кг м
2
2
40.
10. Диаметр диска d =20 см, масса m = 800 г. Определить моментинерции диска относительно оси, проходящей через середину
одного из радиусов перпендикулярно плоскости диска.
Дано:
m = 800 г
d = 20 см
Найти:
I0.
Решение:
Си:
0,800 кг
0,20 м
C
O
IO IC m a 2
m R
IC
2
2
R
a
2
41.
m RR
IO
m
2
2
2
2
3 m R2
IO
4
3 m d
IO
16
2
3 0,800 0,20
3
2
IO
6 10 кг м
16
2



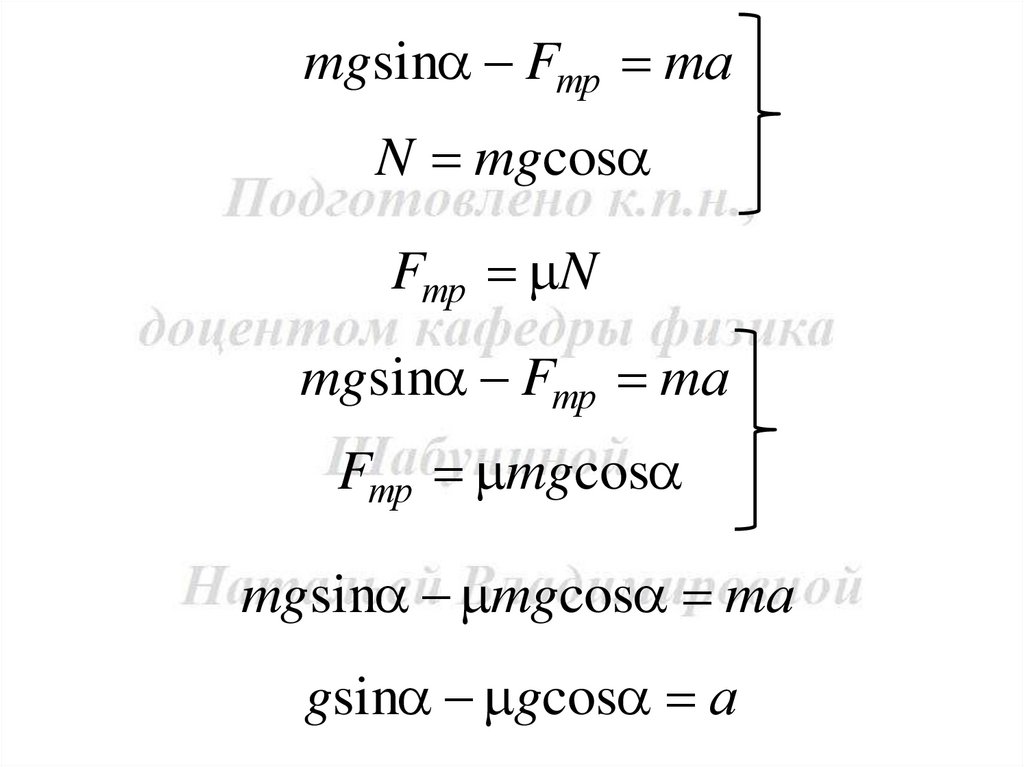










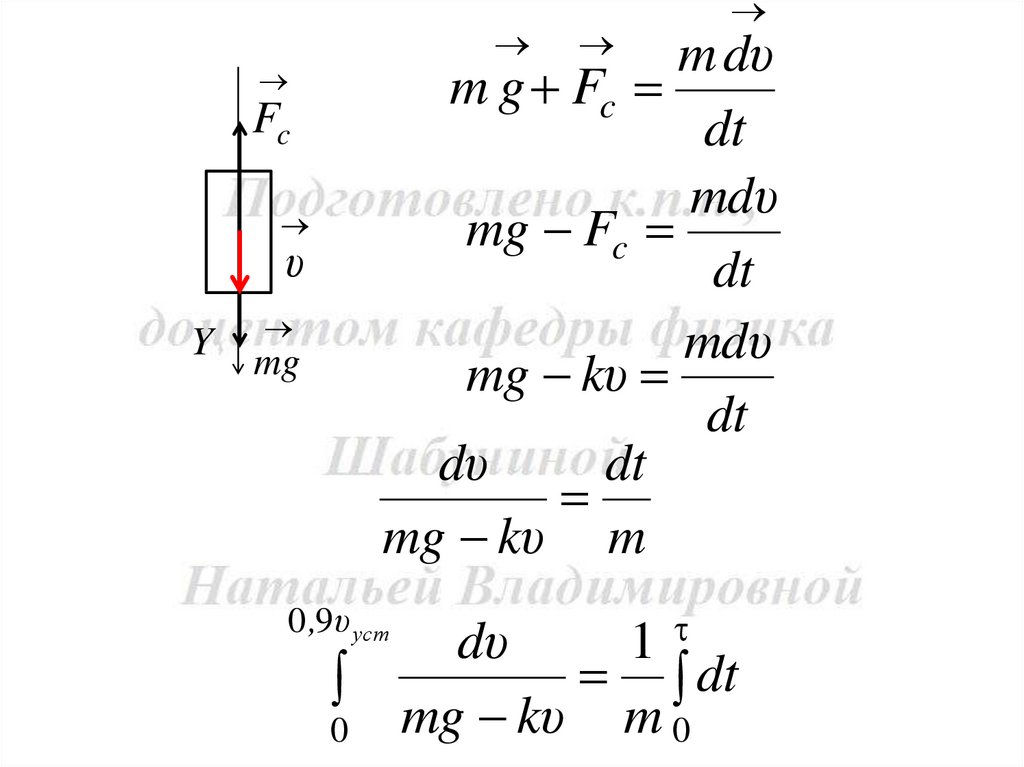








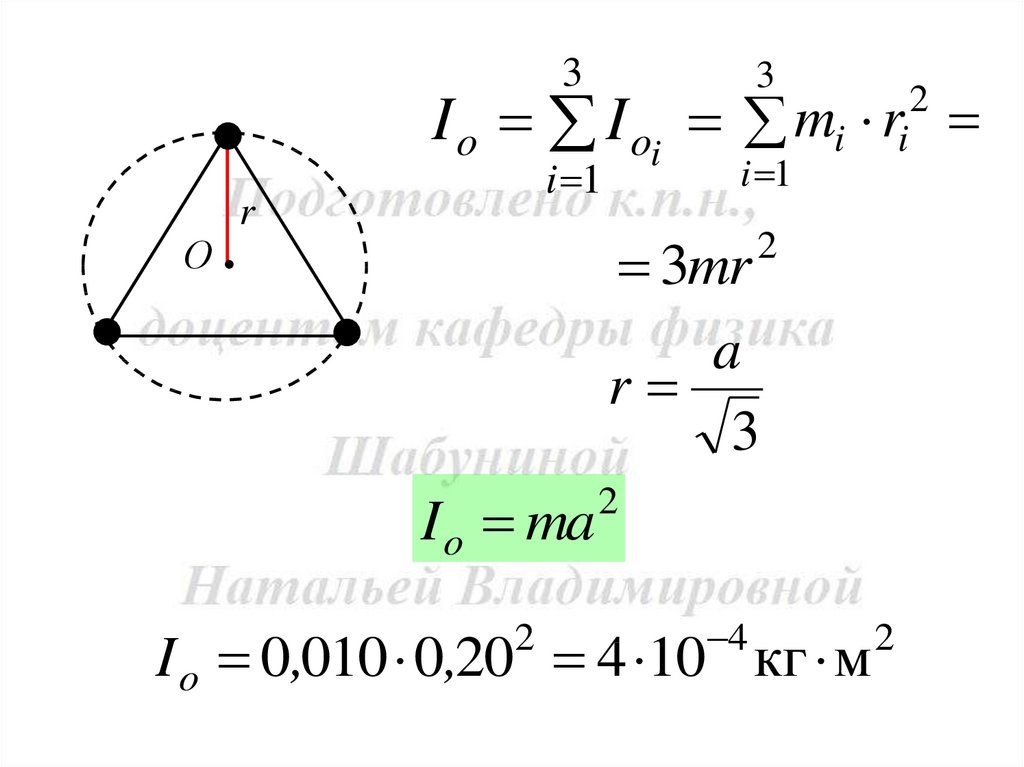



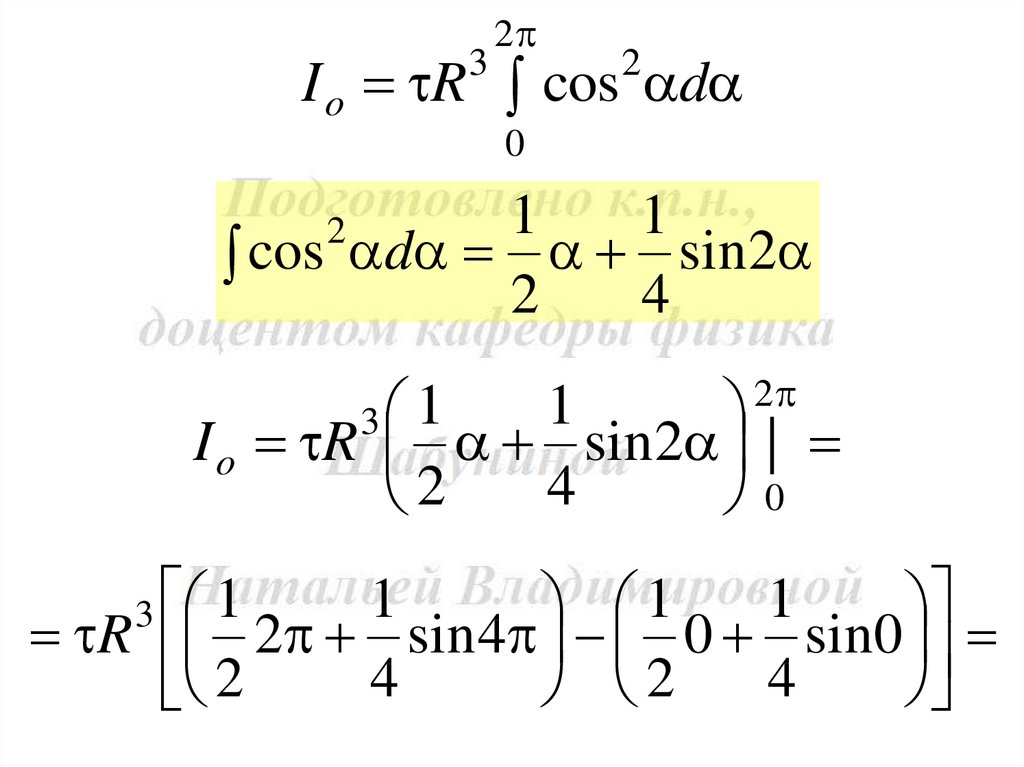
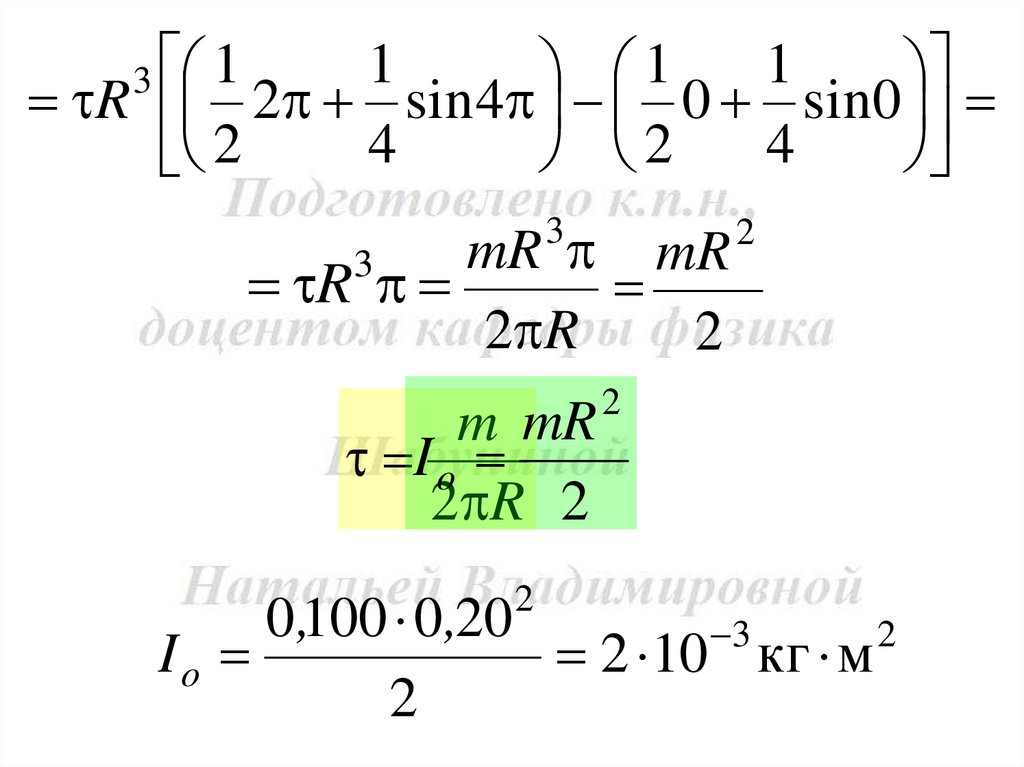


 physics
physics








