Законы Ньютона. Масса и силы

1.

2. Тема 1 Законы Ньютона масса и силы

Основы динамики
составляют три закона
Ньютона -результат
обобщения наблюдений и
опытов в области
механических явлений,
которые были известны еще до
Ньютона и осуществлены
самим Ньютоном

3.

Первый закон Ньютона
(закон инерции)
всякая материальная точка сохраняет состояние покоя или
равномерного и прямолинейного движения до тех пор,
пока воздействие со стороны других тел не выведет ее из
этого состояния
Признак инерциальной системы -отсутствие ускорения
Второй закон Ньютона
dp
F
dt
ОСНОВНОЙ ЗАКОН ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
F ma ,
Третий закон Ньютона
всякое действие материальных точек (тел) друг на
друга носит характер взаимодействия: силы, с которыми действуют друг на
друга тела, равны по модулю, противоположно направлены и действуют
вдоль соединяющей их прямой
Силы приложены к разным телам, их нельзя складывать и вычитать
Силы возникают и исчезают парами и являются силами одной природы
Закон справедлив и в случае взаимодействия на расстоянии

4.

Третий закон справедлив не всегда.
Он выполняется в случаях
1) контактных взаимодействий, т.е. при соприкосновении тел
2) при взаимодействии тел, находящихся на расстоянии друг
от друга, но покоящихся друг относительно друга
Законы Ньютона плохо работают при c
(релятивистская механика) а также, при движении тел очень малых
размеров, сравнимых с размерами элементарных частиц.
Например, нуклоны внутри ядра, кварки внутри нуклонов, и даже
электроны внутри атома, не подчиняются законам Ньютона.

5.

Сила
количественная мера действия одного тела на другое
Под действием сил
0
0
Тела изменяют скорость движения и
приобретают ускорение
(динамическое проявление силы)
Тела деформируются
(статическое проявление силы)
Сила, действующая на тело,
полностью определена,
если указаны ее

6.

Пример 1. Парашютист спускается вертикально с
постоянной скоростью 2 м/с. Систему отсчета,
связанную с Землей, считать инерциальной. В этом
случае
1) вес парашютиста равен нулю
2) сумма всех сил, действующих на парашютиста, постоянна и
не равна нулю
3) сумма всех сил, приложенных к парашютисту, равна нулю
4) сила тяжести, действующая на парашютиста, равна нулю
Ответ:
3
Парашютист равномерно приближается к
земле, когда действие
силы тяжести
компенсируется
силой натяжения строп
парашюта, которая, в свою очередь, обусловлена
сопротивлением воздуха.

7.

Пример 2. Самолет летит по прямой с постоянной
скоростью на высоте 9000 м. Систему отсчета, связанную
с Землей, считать инерциальной. Какое из утверждений
о силах, действующих на самолет, верно?
1)Сила сопротивления воздуха равна силе тяги двигателей
2) сумма всех сил, действующих на самолет, равна нулю
3) на самолет не действуют никакие силы
4) сила тяжести равна силе Архимеда, действующей на
самолет
Ответ: 2

8.

Пример 3. Систему отсчета, связанную с Землей,
будем считать инерциальной. Система отсчета,
связанная с автомобилем, тоже будет инерциальной,
если автомобиль
1)движется равномерно по прямолинейному участку шоссе
2) разгоняется по прямолинейному участку шоссе
3) движется равномерно по извилистой дороге
4) по инерции вкатывается на гору
Ответ: 1

9.

Пример 4. Лошадь тянет телегу. Сравните модули
силы F1 действия лошади на телегу и F2 действия телеги
на лошадь при равномерном движении телеги.
1)F1 = F2
Ответ: 1
2) F1 > F2
3)F1 < F2
4) F1 >> F2

10.

Пример 5. Материальная точка массой 0,5 кг соверша-
ет движение согласно уравнениям x(t ) 3t 3 6t 1,
y (t ) t 2 1, z (t ) 2t 3 1 Определить величину силы,
действующей на точку, в момент времени t=0,5 c
Решение:
По второму закону Ньютона
d 2x
a x 2 9t 2 6 18t
dt
d2y
a y 2 2t 2
dt
d 2z
2
az 2 6t 12t
dt
Ответ: F 5,5Н
a ax2 a y2 az2
F ma
а
18t 2 22 12t 2
а 468t 2 4 11м / с 2
F 0,5 11 5,5Н

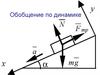
11. Принцип независимости сил

Если на материальную точку действует одновременно
несколько сил, то каждая сообщает материальной точке
ускорение, как будто других сил нет
Эти несколько сил можно заменить
эквивалентной им результирующей силой
n
F Fi
i 1

12.

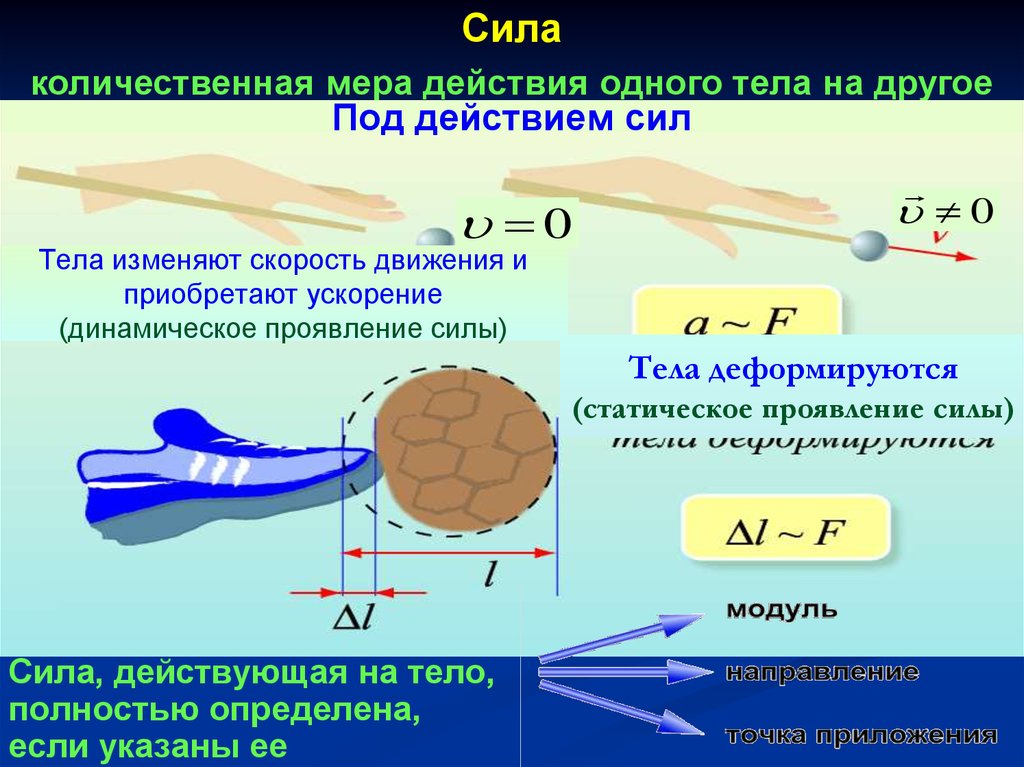
В каком случае лебедь рак и щука действительно не сдвинут
воз, если считать, что силы из равны по модулю ? Силу
трения между землей и возом не учитывать.

13.

В каком случае лебедь рак и щука действительно не
сдвинут воз, если считать, что силы из равны по
модулю ? Силу трения между землей и возом не
учитывать.
Если все три сила расположены в одной плоскости и
угол между ними 1200
Если подъемная сила
лебедя меньше силы
тяжести воза

14.

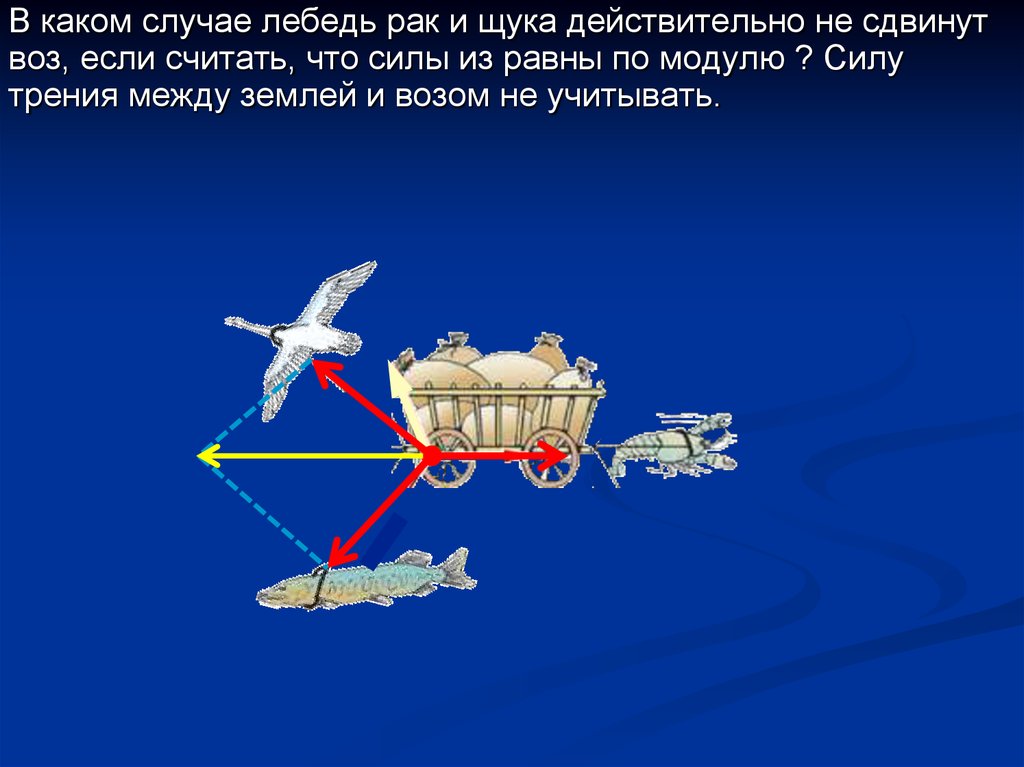
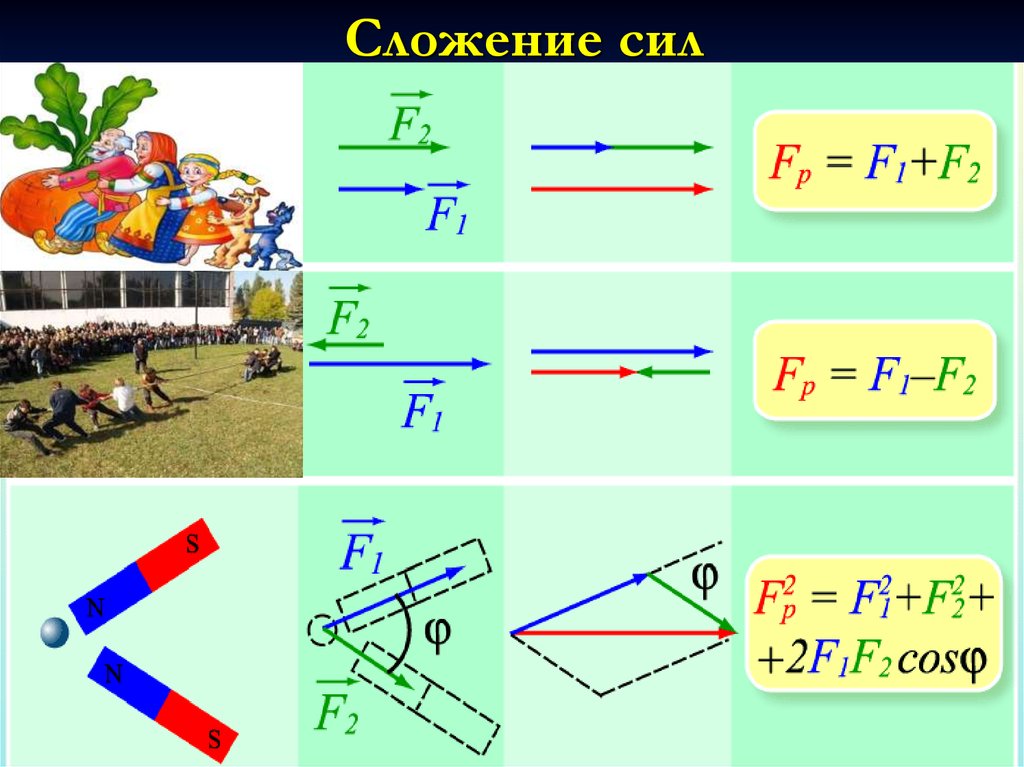
Сложение сил

15. Пример 6. На левом рисунке представлены векторы скорости и ускорения тела в инерциальной системе отсчета. Какой из векторов на

правом рисунке указывает
направление вектора равнодействующей всех сил,
действующих на тело в этой системе отсчета?
а
Ответ: 5

16.

Пример 7. Тело массой 200 г движется равномерно со
скоростью 5 м/с. Чему равна равнодействующая сила,
приложенная к данному телу?
Решение:
const
По первому закону Ньютона
если F 0
Ответ: 0
или
0

17. Пример 8. На рисунке представлен график зависи-мости модуля скорости тела от времени для прямоли-нейно движущегося тела.

Пример 8. На рисунке представлен график зависимости модуля скорости тела от времени для прямолинейно движущегося тела. Равнодействующая всех сил,
действующих на тело, равна нулю на участке(ах)
, м / c
Ответ: На участках OA и BC
О
А
В
С
D
t, c

18.

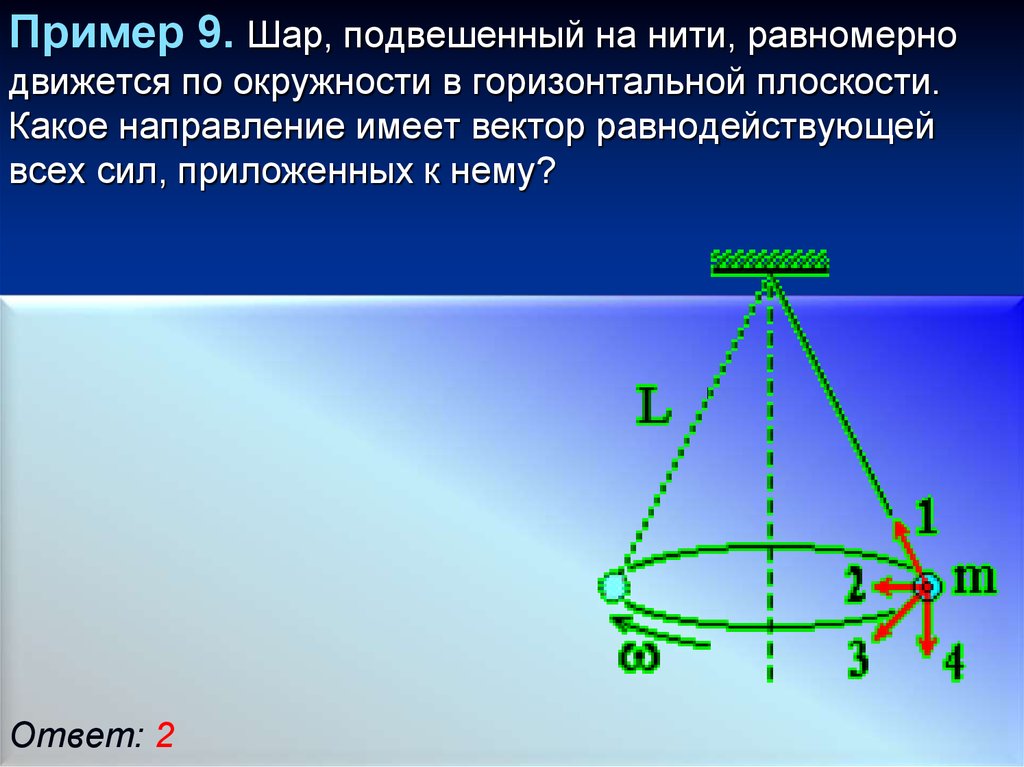
Пример 9. Шар, подвешенный на нити, равномерно
движется по окружности в горизонтальной плоскости.
Какое направление имеет вектор равнодействующей
всех сил, приложенных к нему?
Ответ: 2

19.

Пример 10. Движение легкового автомобиля задано
уравнением х 50 30t 0,6t 2 (все величины в единицах
СИ). Чему равно значение равнодействующей силы,
приложенной к автомобилю? Масса автомобиля 1,5 т.
Решение: По второму закону Ньютона равнодействующая сила
F ma
А ускорение есть вторая производная от перемещения
а х 30 1,2t 1,2 м / c 2
F 1500 1,2 1800 Н
Ответ: 1800 Н

20.

Пример 11. Автомобиль массой 1000 кг движется по выпуклому мосту со скоростью 10 м/c. Радиус кривизны в середине моста 50 м. Определить силу давления автомобиля
на мост в момент прохождения его через середину моста.
Решение: В инерциальной системе отсчета, связанной с поверхностью Земли,
сила
на автомобиль действуют
реакции со стороны моста N и сила тяжести mg та тg N
При криволинейном движении полное ускорение а ан а
2
2
2
По определению ан
В середине моста а 0 а ан
r
N
Если спроектировать все силы на ось
ординат, то : та тg N
2
N тg та т g
r
102
8 кН
N 1000 10
50
Ответ: 8 кН
mg
mа
у

21.

Виды сил в природе
Различают 4 типа сил (взаимодействий)
3
м
гравитационные где 6,67408(31) 10 11
2
m1m2
кг с
тяготения : F 2
r
гравитационная постоянная
значение приведено на 2014 г
электромагнитные
q1q2
электростатические : F k 2
r
упругости : F kx
F N
трения : F
F 2
сильные (ответственное за связь частиц в ядрах)
слабые (ответственное за распад частиц)

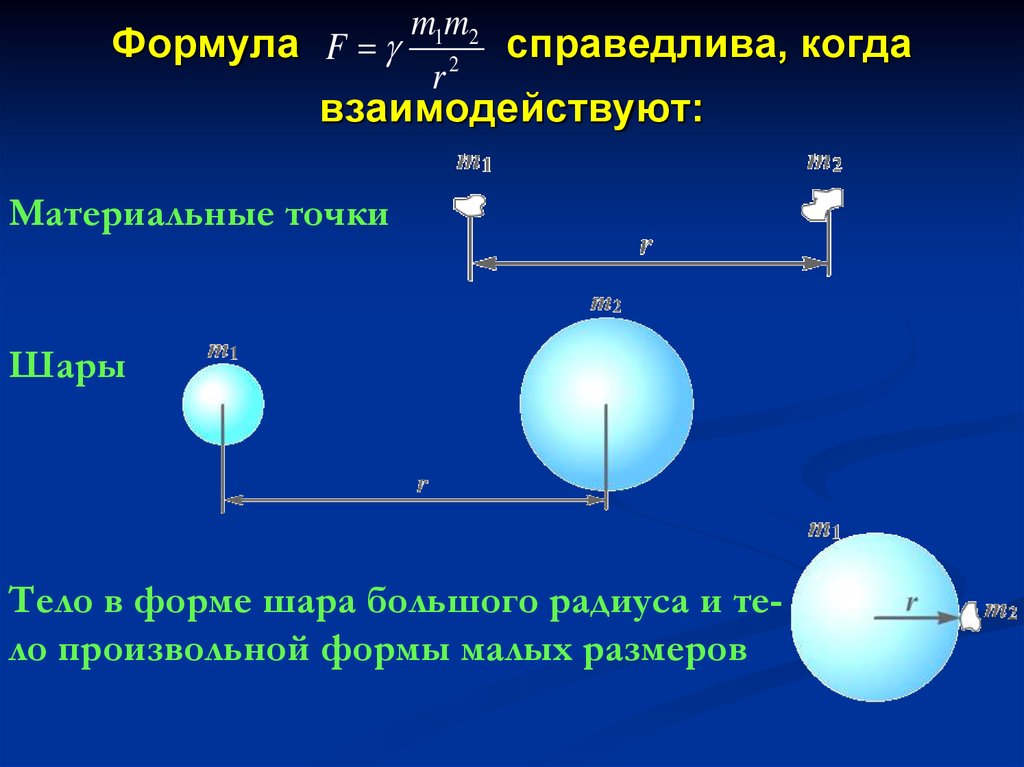
22. Формула справедлива, когда взаимодействуют:

m1m2
Формула F 2 справедлива, когда
r
взаимодействуют:
Материальные точки
Шары
Тело в форме шара большого радиуса и тело произвольной формы малых размеров

23. Любое тело на Земле испытывает действие огром-ного множества сил гравитационного притяжения со стороны окружающих его других

Любое тело на Земле испытывает действие огромного множества сил гравитационного притяжения со
стороны окружающих его других тел
Тяготение между Землей и кошкой массой 3 кг
24
3
5
,
9736
10
M З mк
11
29,9457 H
6
,
67234
10
F
2
6 2
R
6,371 10
Тяготение между Луной и кошкой
(Среднее расстояние между центрами Земли и Луны — 384 467 км)
22
M Л mк
3
7
,
3477
10
11
4
H
F
6
,
67234
10
1
,
04
10
2
2
6
6
R
384,467 10 6,371 10
Тяготение между Солнцем и кошкой (Среднее расстояние между
центрами Земли и Солнца — 149 597 870,66 км)
30
M С mк
3
1
,
9891
10
11
2
H
F
6
,
67234
10
1
,
78
10
2
2
11
6
R
1,496 10 6,371 10
Тяготение между двумя
кошками на расстоянии 10 см
m1m2
11 3 5
F 2 6,67234 10 2 10 7 H
R
0,1

24. Любое тело на Земле испытывает действие огром-ного множества сил гравитационного притяжения со стороны окружающих его других

Любое тело на Земле испытывает действие огромного множества сил гравитационного притяжения со
стороны окружающих его других тел
Тяготение между Землей и кошкой массой 3 кг 29,9457 H
Тяготение между Луной и кошкой 1,04 10 4 H
Тяготение между Солнцем и кошкой 1,78 10 2 H
Тяготение между двумя кошками 10 7 H
Все силы ничтожно малы и
принебрежимы по сравнению
с силой притяжения к Земле.
Ввиду большой важности
этой силы, ей присвоили имя
«собственное»:
сила тяжести тела

25.

Сила гравитации проявляется на Земле в виде силы
тяжести – силы, с которой все тела притягиваются
к Земле
Сила тяжести приложена к телу и действует по прямой,
соединяющей тело с центром Земли
Вблизи поверхности Земли сила тяжести
F тg
т.е. все тела падают с одинаковым ускорением –
ускорением свободного падения g.
м
g 9,819 2
с
Ускорение свободного падения не зависит от массы тела

26. Ускорение свободного падения зависит от

1. Массы планеты
2. Радиуса планеты
3. От высоты над
поверхностью планеты
4. От географической широты
(на полюсах - 9,832 м/с2, на экваторе - 9,78 м/с2)
5. От залежей полезных ископаемых (гравитационные
аномалии обычно выражаются в виде изменения ускорения
свободного падения в их окрестности, что может
свидетельствовать о наличии полезных ископаемых с
бо́льшим значением плотности или, наоборот, о наличии
больших пустот в породах)

27. Пример 12. Каковы силы тяжести, действующие на альпиниста массой 70 кг, находящегося на берегу Желтого моря и на вершине

Эвереста (8852 м)?
Решение: Так как Желтое море и Эверест находятся
примерно на одной широте, то радиус Земли в обоих
точках можно взять одинаковым и равным R 6,371 106 м
F1 mg1
F1 6,67 10
11
Mm
r12
5,9736 10 24 70
6,371 10
6 2
9,7477 70 687,1 H
F2
6,67 10 11 5,9736 10 24 70
6,371 10
6
0,008852 10
9,72 70 685,2 H
Ответ: 687 Н и 685 Н
6 2

28.

Вес
сила, с которой тело вследствие притяжения к
Земле, действует на опору или подвес
Вес и сила тяжести приложены к разным точкам:
вес к подвесу или опоре, сила тяжести – к самому телу
III закон
Ньютона
применим
III закон
Ньютона не
применим
Если подвес (опора) и тело покоятся (двигаются
равномерно прямолинейно)
относительно Земли, то
Р Fтяж
Если имеет место движение с ускорением а, то :
Р Fтяж ma

29.

Пример 13. Какое из нижеприведенных утверждений
справедливо?
1) Вес тела всегда равен его силе тяжести
2) Вес тела всегда больше его силы тяжести
3) Вес тела всегда меньше его силы тяжести
4) Вес тела может быть как больше, так и меньше силы
тяжести, а может быть и равен ей
Ответ: 4

30. Пример 14. В состоянии невесомости

1) масса тела равна нулю
2) на тело не действуют никакие силы
3) сила тяжести равна нулю
4) вес тела равен нулю
Ответ: 4

31. Пример 15. Чемодан массой 5 кг стоит на полу лифта, движущегося с ускорением 1 м/с2. Найти вес чемодана, ес-ли лифт движется

Пример 15. Чемодан массой 5 кг стоит на полу лифта,
движущегося с ускорением 1м/с2. Найти вес чемодана, если лифт движется вверх равноускоренно/замедленно
равноускоренно
7
Решение: 1) Лифт движется
по II закону Ньютона ma N mg
В проекции на ось Оу: ma N mg
N m a g
по III закону Ньютона
P N
a
y
P m( a g ) 5 (1 10) 55( H )
P mg
2) Лифт движется равнозамедленно
по II закону Ньютона ma N mg
ma N mg
N m a g
В проекции на ось Оу:
по III закону Ньютона P N
P1 m ( g а) 5 (10 1) 45( H )
P mg
mNg
Р

32. Пример 16. Чемодан массой 5 кг стоит на полу лифта, движущегося с ускорением 1 м/с2. Найти вес чемодана, ес-ли лифт движется

Пример 16. Чемодан массой 5кг стоит на полу лифта,
движущегося с ускорением 1 м/с2. Найти вес чемодана, если лифт движется вниз равноускоренно/равнозамедленно
равнозамедленно
Решение: 1) Лифт движется
по II закону Ньютона ma N mg
В проекции на ось Оу:ma N mg
N m a g
по III закону Ньютона P N
a
y
P m( a g ) 5 (1 10) 55( H )
P mg
2) Лифт движется равноускоренно
по II закону Ньютона ma N mg
В проекции на ось Оу: ma N mg
N m a g
по III закону НьютонаP N
P1 m ( g а) 5 (10 1) 45( H )
P mg
N
mg
Р

33. Пример 17. Чемодан массой 5 кг стоит на полу падающего лифта

Пример 17. Чемодан массой 5кг стоит на полу
падающего лифта
Решение: по II закону Ньютона
mg N mg
В проекции на ось Оу:
g
y
mg N mg
N 0
по III закону Ньютона
P N
Следовательно,
P 0
Т.е. чемодан (вместе с лифтом)
находится в состоянии невесомости
N
mg
Р

34. Пример 18. Если тело находится в состоянии покоя внутри жидкости или газа, и сила тяжести уравновеши-вается выталкивающей

Пример 18. Если тело находится в состоянии покоя
внутри жидкости или газа, и сила тяжести уравновешивается выталкивающей силой, то можно ли считать, что
это тело находится в состоянии невесомости?
Решение: Состояние невесомости
характеризуется отсутствием в
теле внутренних напряжений – т.е.
отдельные слои тела не давят
друг на друга и на опору
В теле, плавающем внутри жидкости,
внутренние напряжения,
существующие в нем за счет
силы тяжести, не исчезают
Тело давит на жидкость или газ,
являющиеся в данном случае
опорой
Ответ: нет

35.

Пример 24. Человек испытает состояние невесомости
1) если будет двигаться с ускорением, равным по величине g
2) если будет двигаться с любым ускорением, направленным
вниз
3) в течении всего затяжного прыжка до открытия парашюта
4) в начальный момент свободного падения в атмосфере,
когда сопротивление воздуха ещё невелико
5) при полёте в самолёте, движущегося по баллистической
траектории (траектория, по которой летел бы самолет под
воздействием одной лишь силы земного притяжения)
Для тренировки космонавтов в России и США создают кратковременное
состояние невесомости (до 40 с) при полётах самолёта по баллистической
траектории. В кабине пилота на нитке подвешен грузик. Когда нить не
натянута - состояние невесомости. Пилот должен управлять самолётом
так, чтобы шарик висел в воздухе, а нить не была натянута, т.е. самолёт
должен иметь постоянное ускорение g, направленное вниз (самолёт
«падает» вместе с шариком, ниткой, пилотом и космонавтами).
Состояние невесомости можно ощутить в начальный момент свободного
падения тела в атмосфере, когда сопротивление воздуха ещё невелико.
Ответ: 4, 5

36.

Пример 19. Почему космонавты, находящиеся на Международной космической станции (350 км от поверхности
Земли) испытывают состояние невесомости?
1. На такой высоте гравитация исчезает
2.Состояние невесомости на МКС возникает за счёт движения по круговой орбите с первой космической скоростью
Решение: ускорение свободного падения на МКС
M
3 5,9736 1024
м
11
g МКС 2 6,67234 10
8,8 2
2
6
6
R
с
6,371 10 0,35 10
что всего лишь на 10 % меньше, чем на поверхности Земли.
Состояние невесомости на МКС возникает за счёт движения
по круговой орбите с первой космической скоростью.
Ответ: 2

37.

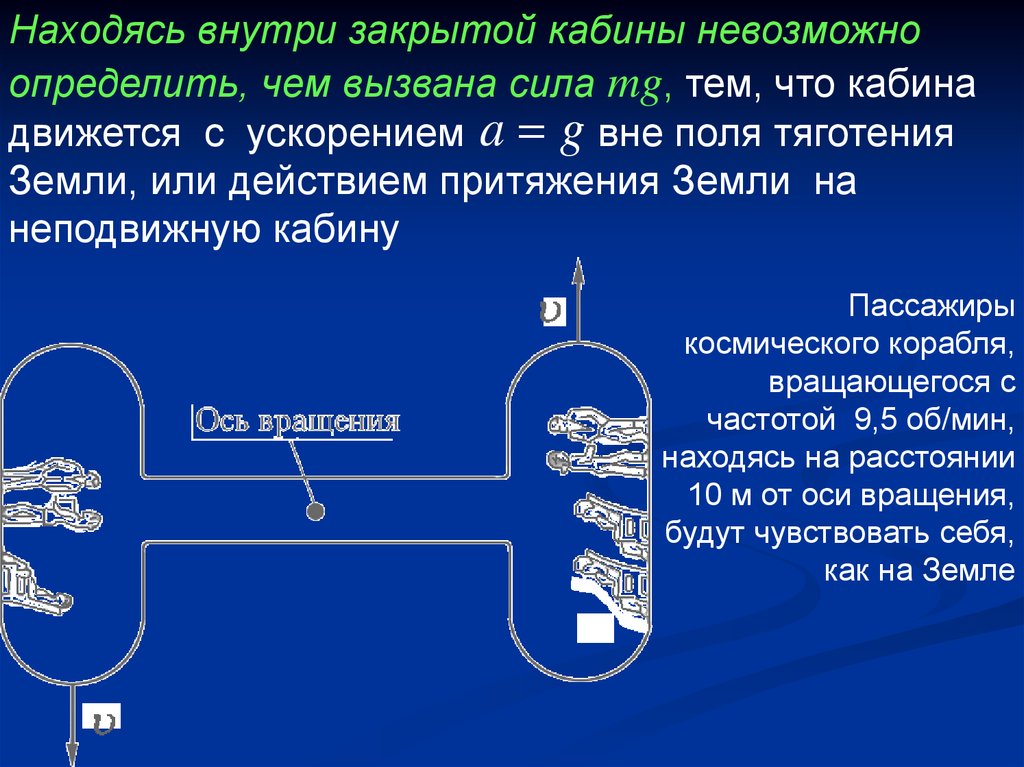
Находясь внутри закрытой кабины невозможно
определить, чем вызвана сила mg, тем, что кабина
движется с ускорением a g вне поля тяготения
Земли, или действием притяжения Земли на
неподвижную кабину
Пассажиры
космического корабля,
вращающегося с
частотой 9,5 об/мин,
находясь на расстоянии
10 м от оси вращения,
будут чувствовать себя,
как на Земле

38.

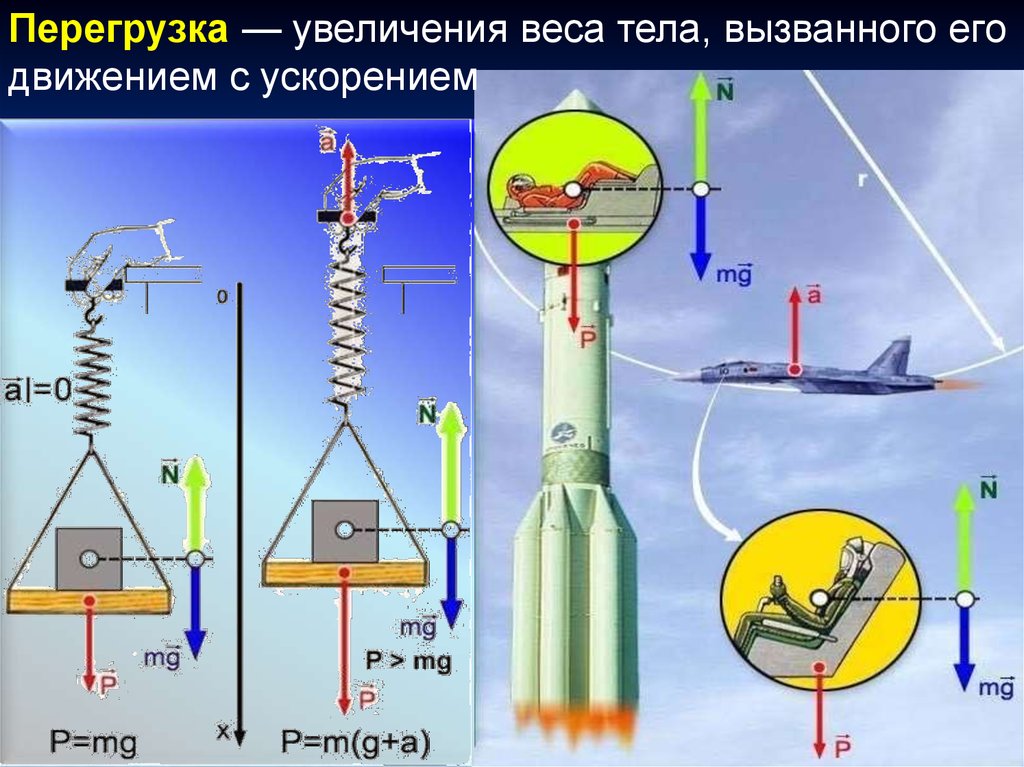
Перегрузка — увеличения веса тела, вызванного его
движением с ускорением

39.

Перегрузка, не связанная с
ускорением

40.

Примерные значения перегрузок, встречающихся в жизни
Человек, стоящий неподвижно
1g
В гонках на картах перегрузки
в поворотах достигают 3–4 g
Пассажир в самолете при взлете
Центрифуга ЦФ-18. Масса вращающихся
частей - 300 т, радиус плеча - 18 м.
Максимальная перегрузка - 30g.
Космонавт при спуске в космическом корабле «Союз»
Макс. перегрузка при тренировке
5 g в направлении «голова-таз»
Летчик при выполнении фигур высшего пилотажа
8 g в направлении
«грудь-спина»
Парашютист при раскрытии парашюта (при изменении скорости от 60 до 5 м/с)
1,5g
3g-4g
До 5g
5g
МАХ (кратковременная) перегрузка, при
которой человеку удалось выжить- 214 g
Летчик при выведении самолета из пикирования
8g-9g
Перегрузка (длительная), соответствующая пределу физиологических
возможностей человека
8g-10g

41. Пример 20. Ракета массой 105 кг стартует верти-кально вверх с поверхности Земли с ускорением 15 м/с2. Если силами сопротивления

Пример 20. Ракета массой 105 кг стартует вертикально вверх с поверхности Земли с ускорением 15 м/с2.
Если силами сопротивления воздуха при старте
пренебречь, то сила тяги двигателей ракеты равна
Решение:
Проставим силы, действующие на ракету
тa F тg
В проекции на ось у:
тa F тg
F т g а 105 10 15 2,5 106 Н
Ответ: 2,5 106 Н
у
F
тa
тg

42.

2. Электромагнитные силы
Электромагнитные силы проявляют себя как
упругие силы и силы трения

43. Упругие силы

Под действием внешних сил возникают
деформации (изменение размеров и
формы) тел
Если после прекращения действия
внешних сил восстанавливаются прежние форма и размеры
тела, то деформация называется упругой
Деформация имеет упругий характер, если внешняя сила не
превосходит определенного значения, которая называется
пределом упругости
Деформация, которая сохраняется в теле
после прекращения действия внешних сил,
называется пластической

44.

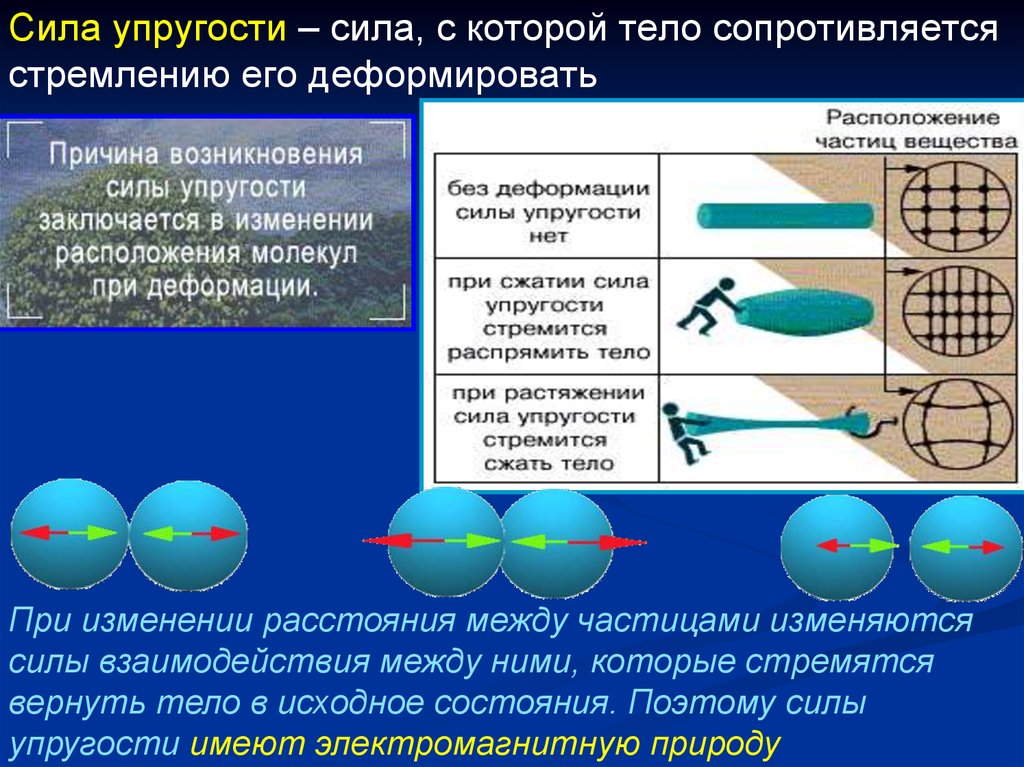
Сила упругости – сила, с которой тело сопротивляется
стремлению его деформировать
При изменении расстояния между частицами изменяются
силы взаимодействия между ними, которые стремятся
вернуть тело в исходное состояния. Поэтому силы
упругости имеют электромагнитную природу

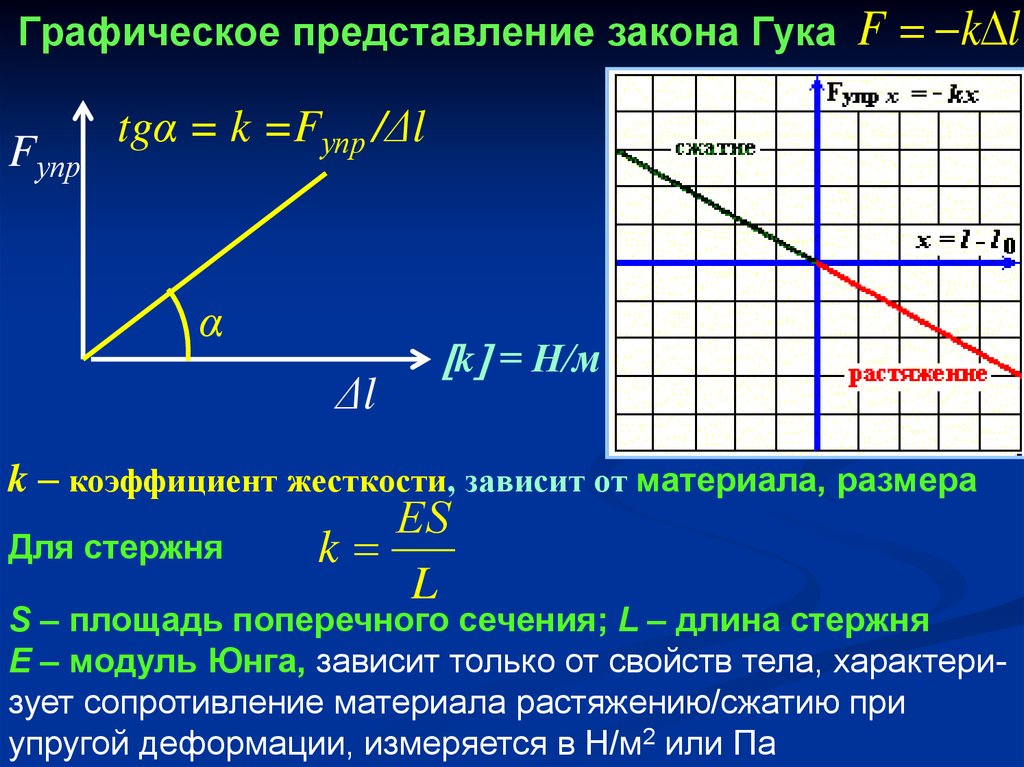
45. Графическое представление закона Гука

Fупр
F k l
tgα = k =Fупр /Δl
α
Δl
k = Н/м
k – коэффициент жесткости, зависит от материала, размера
Для стержня
ЕS
k
L
S – площадь поперечного сечения; L – длина стержня
E – модуль Юнга, зависит только от свойств тела, характеризует сопротивление материала растяжению/сжатию при
упругой деформации, измеряется в Н/м2 или Па

46.

Пример 21. Как изменится жесткость пружины при
уменьшении сил, приложенных к ее концам в два раза?
Решение:
жесткость конкретной пружины есть величина
постоянная, так как жесткость зависит от длины
пружины
материала
Ответ: не изменится

47.

Пример 22. Однородную пружину длиной L и
жесткостью k разрезали на 3 равные части. Чему равна
жесткость каждой части пружины?
ЕS
k
L
Решение:
k1
Ответ: 3K
3
ЕS 3ЕS
3k
L
L
3

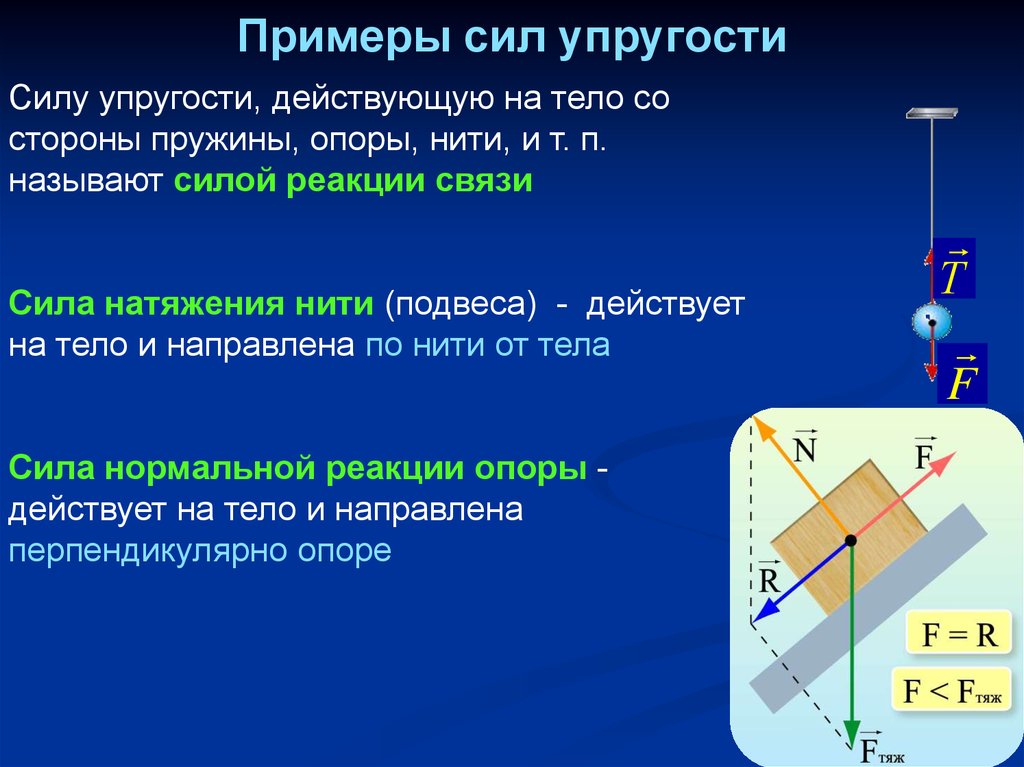
48. Примеры сил упругости

Силу упругости, действующую на тело со
стороны пружины, опоры, нити, и т. п.
называют силой реакции связи
Сила натяжения нити (подвеса) - действует
на тело и направлена по нити от тела
Сила нормальной реакции опоры действует на тело и направлена
перпендикулярно опоре
Т
F

49.

Пример 23. К невесомой нити подвешен груз массы 1
кг. Точка подвеса нити движется равноускоренно
вертикально вниз с ускорением 4 м/с2. Чему равно
натяжение нити?
Решение: Рассмотрим силы
На груз действуют сила натяжения нити Т
И сила тяжести mg
Результирующая этих сил F заставляет груз
двигаться с ускорением a
Уравнение сил mа Т mg ,
y
Движение осуществляется по вертикали вдоль Оу
Проекции сил на Оу:
Ответ: 6 Н
mа Т mg,
Т m а g
Т m а g 1 4 10 6 Н
Т
а
F
mg

50.

Пример 24. В шахте опускается равноускоренно лифт
массой 280 кг. В первые 10 с он проходит 35 м. С какой
силой канат действует на закрепленный вверху блок?
Решение: Т.к. в данной задаче масса каната не указана, т.е. считается пренебрежимо малой в сравнением с массой лифта,
то силу натяжения каната считают одинаковой по
y
Т Т
всей длине
На тело действуют силы mа Т mg ,
Движение осуществляется по вертикали вдоль Оу
Проекции сил на Оу: mа Т mg, Т m а g
Поскольку по условию за первые 10 с лифт равноускоренно проходит 35 м, то движение подчиняется закону:
at 2
S
2
2S
a 2
t
Ответ: 2,6 кН
2S
Т m 2 g
t
2 35
Т 280
10 2604 Н
2
10
Т
mа
Т
mg

51.

Пример 25. Через неподвижный блок перекинута
невесомая нерастяжимая нить, к концам которой
подвешены грузики равной массы, 5 кг каждый. Чему
равна сила натяжения нити?
Решение: Т.к. тела связаны невесомой нитью (масса блока тоже
не учитывается), то силу натяжения нити считают одинаковой по
всей длине Т1 Т 2 Т1 Т 2
Уравнение сил
mа Т mg ,
Т.к. тела уравновешивают друг друга, то
система находится в состоянии покоя и
ускорение грузиков равно нулю. Тогда в
проекции на ось у получаем
0 Т mg,
Т 1
Т 2
Т1
Т2
Т mg ,
Т 5 10 50 Н
Ответ: 50Н
y
m1 g
m2 g

52.

Пример 26. Через неподвижный блок перекинута
невесомая нерастяжимая нить, к концам которой
подвешены грузики массами 2 кг и 3 кг соответственно.
Чему равна сила натяжения нити?
Решение: Т.к. тела связаны невесомой нитью, то сила натяжения
нити одинакова по всей длине Т1 Т 2 Т1 Т 2
Т.к. массы грузиков не равны, то они движутся с
ускорениями а1 и а2. Т.к. нить нерастяжима, то заy
одно и то же время грузы проходят одинаковый
путь S1=S2, или для равноускоренного движения
Т 1
at 2
S
2
a1t 2 a2t 2 откуда a a
1
2
2
2
Т
g
В проекции на Оу: m1a Т m1 g , a
а 1
Т1
m1
Т
m2 a Т m2 g , m2 g Т m2 g
m1
2т1m2 g 2 2 3 10
m1 g
Т
24 Н
т1 m2
Ответ: 24Н
2 3
Т 2
а
2
Т2
m2 g

53.

Пример 26. К пружинным весам подвешен блок. Через
блок перекинут нерастяжимый шнур с грузами массой 2 кг и
3 кг на концах. Каково будет показание весов во время
движения грузов? Массой блока и шнура пренебречь.
Решение.
a a
m1a m1 g T1
m2 a m2 g T2
0 T T F
1
2
упр
m1a m1 g T
m2 a m2 g T
0 2T F
упр
1
Fупр
Вычтем из среднего уравнения верхнее:
g m2 m1 a m2 m1
a
g m2 m1
m2 m1
Подставим во второе уравне2 gm1m2
ние полученное значение а:
T
m2 m1
Из третьего уравнения:
4 gm1m2 По определению вес чисFупр 2T
m2 m1 ленно равен силе, с которой растянута пружина:
4 gm1m2
P
47,04 H
m2 m1
2
T1
T2
a2
T2
T1
m1g
a1
y
m2 g
Т1 Т 2 Т1 Т 2

54.

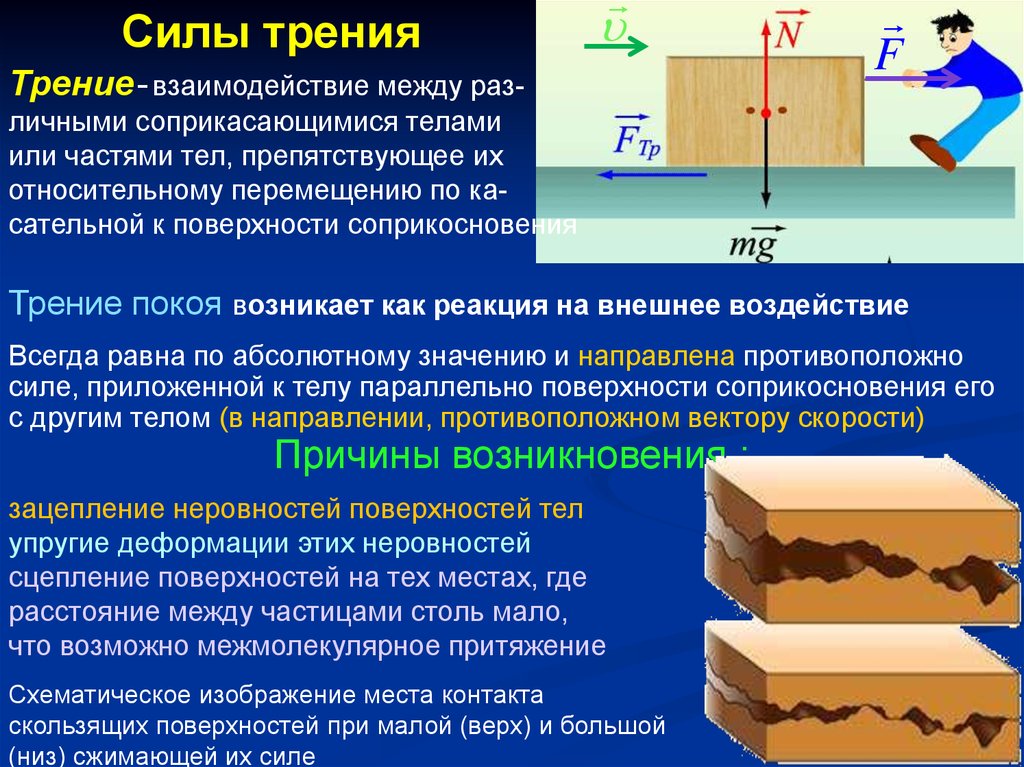
Силы трения
Трение- взаимодействие между раз-
F
личными соприкасающимися телами
или частями тел, препятствующее их
относительному перемещению по касательной к поверхности соприкосновения
Трение покоя возникает как реакция на внешнее воздействие
Всегда равна по абсолютному значению и направлена противоположно
силе, приложенной к телу параллельно поверхности соприкосновения его
с другим телом (в направлении, противоположном вектору скорости)
Причины возникновения :
зацепление неровностей поверхностей тел
упругие деформации этих неровностей
сцепление поверхностей на тех местах, где
расстояние между частицами столь мало,
что возможно межмолекулярное притяжение
Схематическое изображение места контакта
скользящих поверхностей при малой (верх) и большой
(низ) сжимающей их силе

55.

По величине сила трения покоя может изменяться от нуля до
некоторого максимального значения
Максимальная сила трения покоя пропорциональна силе,
действующей перпендикулярно поверхности соприкосновения тел –
силе нормальной реакции опоры
Fтр.скольжения Fmax тр.покоя N
коэффициент трения
график зависимости модуля силы
трения от величины внешней силы
Fтр
Fmax тр. покоя
Fв неш 0 Fтр 0
Fв неш F1 Fтр Fтр 1
Fв неш F2 Fтр Fтр 2
Fвнеш Fдвиж Fтр Fmax тр. покоя
Fв неш Fдв иж Fтр Fтр. скол ьжения
Fтр 2
Fтр1
Fтр. скол ьжения
Трение
скольжения
Трение
покоя
F1 F2 Fдв иж
Fв неш

56.

Трение скольжения
сила, возникающая при поступательном перемещении
одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения
Fтр.скольжения N
коэффициент трения для данных поверхностей, зависит от
материала трущихся поверхностей
качества обработки их поверхностного слоя
в меньшей степени
от температуры
относительной скорости перемещения
не зависит от
площади соприкасающихся поверхностей
N — сила нормальной реакции опоры
зависит от площади пятна контакта и давления

57.

Пример 27. Для силы трения покоя всегда
справедливо соотношение:
1) F N
2) F N
3) F mg
4) F mg
Решение: так как максимальное значение силы трения
покоя
Fmax тр.покоя N
то
Ответ: 1
Fтр.покоя N

58.

Пример 28. Автомобиль приближается к повороту радиуса 50 м. Рассчитайте предельные скорости при повороте на сухой дороге (μ=0,5) и на скользкой дороге (μ=0,2)
.Решение: В инерциальной системе
отсчета, связанной с
поверхностью Земли, на автомобиль
реакции со стороны моста N ,
сила тяжести mg и сила трения покоя Fтр
действуют сила
r
а
N
Ускорение обусловлено равнодействующей
всех
приложенных к автомобилю сил та тg N Fтр
Ускорение направлено вдоль
2
радиуса кривизны траектории а ан
r
В проекции на Оу: 0 тg N
В проекции на Ох: та Fтр
По определению: Fтр N
2
m тg rg
r
Ответ: 20 м/c и 12,6 м/с
mg
Fтр
1 0,5 80 10 20 м с
2 0,2 80 10 12,6 м с
х
у

59.

Пример 29. Если на тело массой 10 кг, лежащее на
горизонтальной плоскости, подействовать горизонтальной силой 20 Н, то сила трения между телом и
плоскостью будет равна (коэффициент трения между
телом и плоскостью 0,3)
Решение: Из условия задачи не понятно, сдвинулось тело
или нет.
Если F Fmax тр
, то
F Fmax тр
, то
Если
у
Fтр F
Fтр Fmax тр N
В проекции на Оу: 0 N mg N mg
Fmax тр mg
F Fmax тр
N
Fтр
mg
F
х
Fmax тр 0,3 10 10 30 Н
следовательно
Fтр 20 Н
Ответ: 20 Н

60.

Пример 30. На горизонтальной поверхности находится
тело массой 2 кг. На тело действует горизонтально направленная сила величиной 10 Н. Под действием этой
силы, тело перемещается с ускорением а=5 м/с2. Определить коэффициент трения между телом и поверхностью.
Решение: ma F N Fтр mg
В проекции на Ох:
mа F Fтр
В проекции на Оу: 0
у
Fтр N
а
N
Fтр
mg
F
N mg
N mg
Fтр mg
F ma 10 2 5
0
2 10
mg
mg
Fтр
х
Ответ: 0

61.

Пример 31. Брусок массой т движется равноускоренно
по горизонтальной поверхности под действием силы F,
направленной под углом α, как показано на рис. Коэффициент трения скольжения равен μ. Чему равен модуль
силы трения?
Решение: Силы, действующие на брусок
ma F N Fтр mg
В проекции на Ох:
В проекции на Oу:
ma F cos Fтр
0 N mg F sin
у
Fтр N
N mg F sin
а
Fтр
Отсюда сила трения
N
mg
Fтр mg F sin
F
х

62.

Пример 32. Брусок массой т движется равноускоренно
по горизонтальной поверхности под действием силы F, направленной под углом α, как показано на рис.
Коэффициент трения скольжения равен μ. Чему равен
модуль силы трения?
Решение:
В проекции на Ох:
В проекции на Oу:
у
ma F N Fтр mg
ma F cos Fтр
Fтр N
0 N mg F sin
N mg F sin
Отсюда сила трения
а
Fтр
N
mg
Fтр mg F sin
F
х

63.

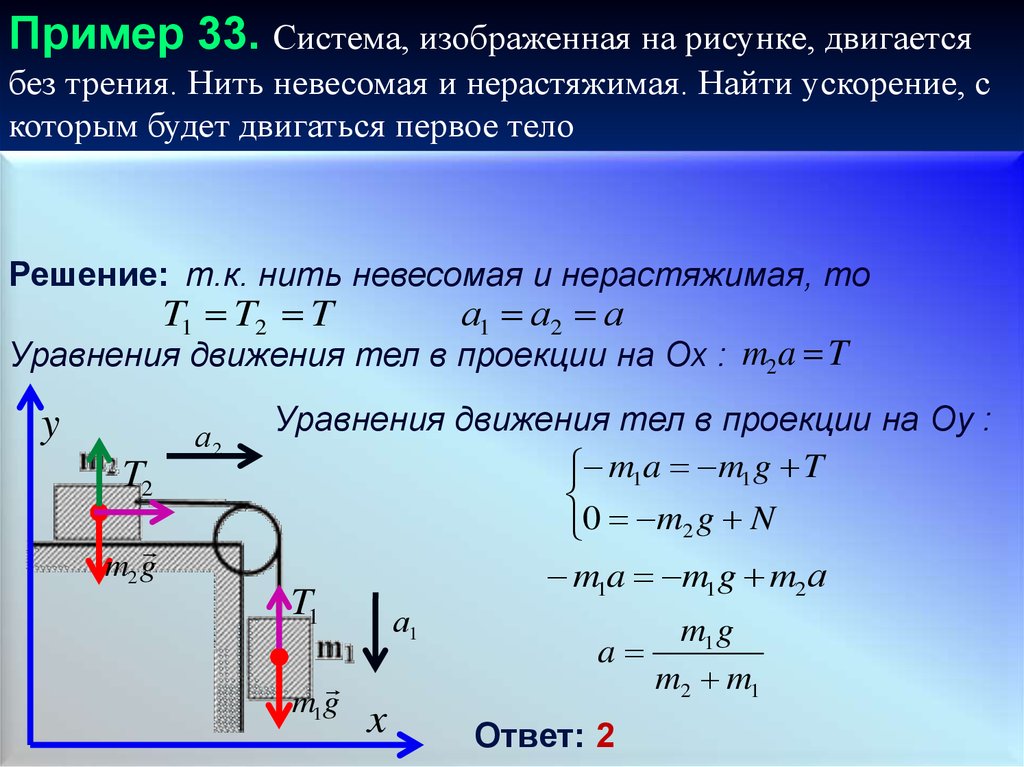
Пример 33. Система, изображенная на рисунке, двигается
без трения. Нить невесомая и нерастяжимая. Найти ускорение, с
которым будет двигаться первое тело
Решение: т.к. нить невесомая и нерастяжимая, то
T1 T2 T
а1 а2 а
Уравнения движения тел в проекции на Ox : m2 a T
y
а2
T2
m2 g
Уравнения движения тел в проекции на Oу :
m1a m1 g T
0 m2 g N
m1a m1 g m2 а
T1
m1g
а1
x
m1 g
a
m2 m1
Ответ: 2

64.

Пример 34. Система, изображенная на рисунке, дви-гается
по шероховатой поверхности с коэффициентом трения µ. Нить
невесомая и нерастяжимая. Найти ускорение, с которым будет
двигаться первое тело
Решение:
т.к. нить невесомая и нерастяжимая, то
T1 T2 T
а1 а2 а
Уравнения движения тел в проекции на Ox : m2 a T Fтр
y
Уравнения движения тел в проекции на Oу :
а2
m1a m1 g T
N T2
m1a m1 g m2 а Fтр
0 m2 g N
Fтр N m2 g
Fтр m2 g
T1
m1g
а1
a
x Ответ: 2
m1 g Fтр
m2 m1
m1 g m2 g
m2 m1

65.

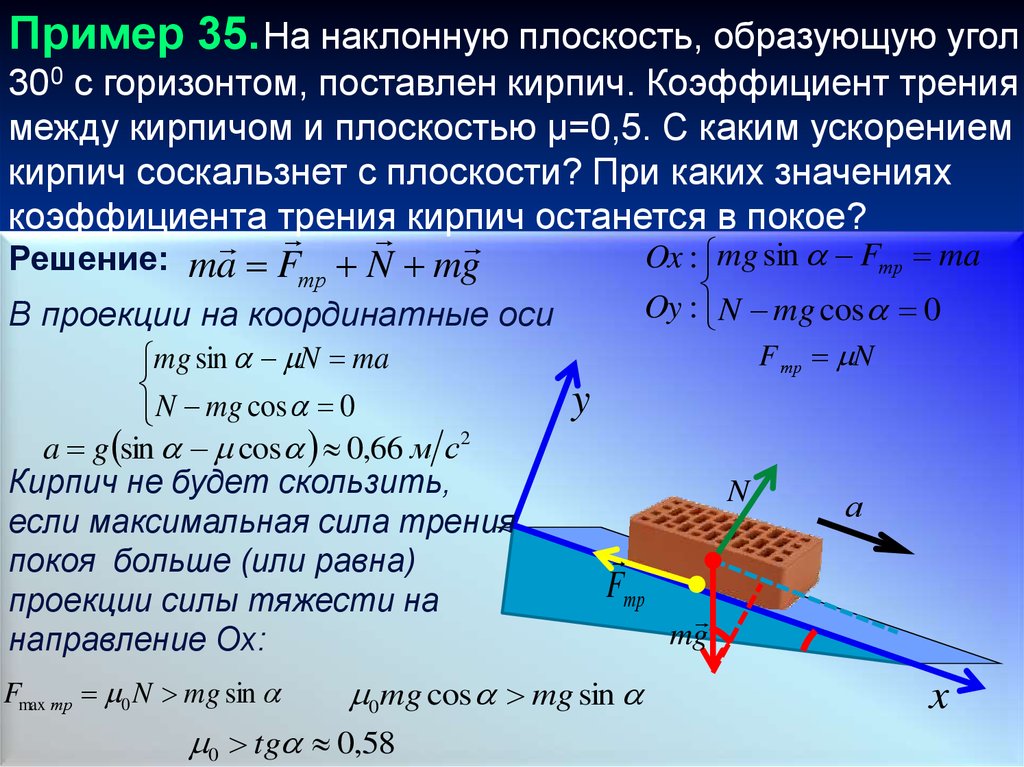
Пример 35. На наклонную плоскость, образующую угол
300 с горизонтом, поставлен кирпич. Коэффициент трения
между кирпичом и плоскостью μ=0,5. С каким ускорением
кирпич соскальзнет с плоскости? При каких значениях
коэффициента трения
кирпич останется в покое?
Решение: ma F N mg
тр
В проекции на координатные оси
mg sin N ma
N mg cos 0
a g sin cos 0,66 м с2
Кирпич не будет скользить,
если максимальная сила трения
покоя больше (или равна)
проекции силы тяжести на
направление Ox:
Fmax тр 0 N mg sin
Ox : mg sin Fтр ma
Oy : N mg cos 0
F тр N
y
N
Fтр
0mg cos mg sin
0 tg 0,58
а
mg
x

66. Пример 36. Невесомый блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы α=300 и β=450. Гири

массы т1 и т2 соединены нитью и
перекинуты через блок. Сила натяжения нити 6 Н. Найти
ускорение, с которым движутся гири и массы гирь, если гири
одинаковы. Коэффициенты трения гирь µ1=µ2=0,1.
Решение: Пусть гиря 2 скользит вниз, а гиря 1 – вверх.
Уравнения движения гирь в проекции на направления
их движения :
m2 g sin T2 Fтр2 m2 a,
Учитывая, что
T1 m1 g sin Fтр1 m1a.
T1 T2 T
m2 g sin T 2 m2 g cos m2 a N1 a
поскольку нить невесома
T m1 g sin 1m1 g cos m1a
Сложим уравнения системы
почленно:
Fтр1
Fтр1 1 N1 1m1 g cos
Fтр2 2 N 2 2 m2 g cos
T1
T1
m1g
a m2 m1 g m2 sin m1 sin 2m2 cos 1m1 cos
T2
a
T2
N2
Fтр2
m2 g

67. Пример 36. Невесомый блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы α=300 и β=450. Гири

массы т1 и т2 соединены нитью и перекинуты
через блок. Сила натяжения нити 6 Н. Найти ускорение, с
которым движутся гири и массы гирь, если гири одинаковы.
Коэффициенты трения гирь µ1=µ2=0,1.
g m2 sin m1 sin 2 gm2 cos 1m1 cos
a
m2 m1
Т.к. по условию m1 m2 m
g sin sin 2 cos 1 cos
м
a
2
0,244 2
с
Подставим полученное значение ускорения во второе
уравнение системы и выразим массу грузов:
2T
m
1 кг
g sin sin 1 cos 2 cos

68.

Сила трения качения
сила, возникающая при качении (без скольжения) твердых
тел круглой формы по поверхности других твердых тел
Причина возникновения:
Под действием силы тяжести круглое твердое тело (шар или колесо),
находящееся на плоской поверхности, деформируется, вследствие чего
оно опирается не на одну точку, а на площадку больших или меньших
размеров. Модуль силы трения качения:
Fтр.качения
N
R
- безразмерный коэффициент трения качения
N - модуль нормальной составляющей силы реакции опоры
R- радиус катящегося тела

69.

Если мы сравним между собой коэффициенты всех видов
внешнего трения для каких-либо двух материалов, из которых
изготовлены соприкасающиеся тела, то
покоя скольжения качения
т. е. при прочих равных условиях наибольшим является
трение покоя, а наименьшим - трение качения.

70.

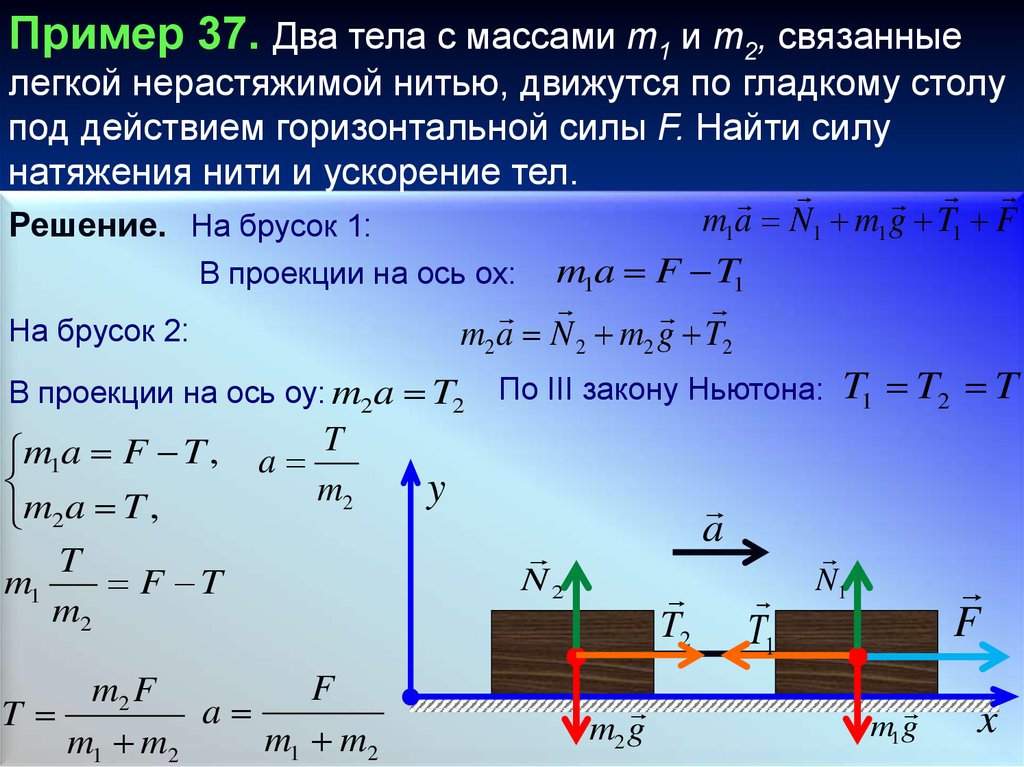
Пример 37. Два тела с массами т1 и т2, связанные
легкой нерастяжимой нитью, движутся по гладкому столу
под действием горизонтальной силы F. Найти силу
натяжения нити и ускорение тел.
m1a N1 m1 g T1 F
Решение. На брусок 1:
В проекции на ось ох: m1a F T1
На брусок 2:
m2 a N 2 m2 g T2
В проекции на ось оу: m2 a T2
m1a F T ,
m2 a T ,
T
m1
F T
m2
T
a
m2
F
m2 F
a
T
m1 m2
m1 m2
По III закону Ньютона:
y
a
N2
T2
m2 g
T1
T1 T2 T
N1
F
m1g
x

71.

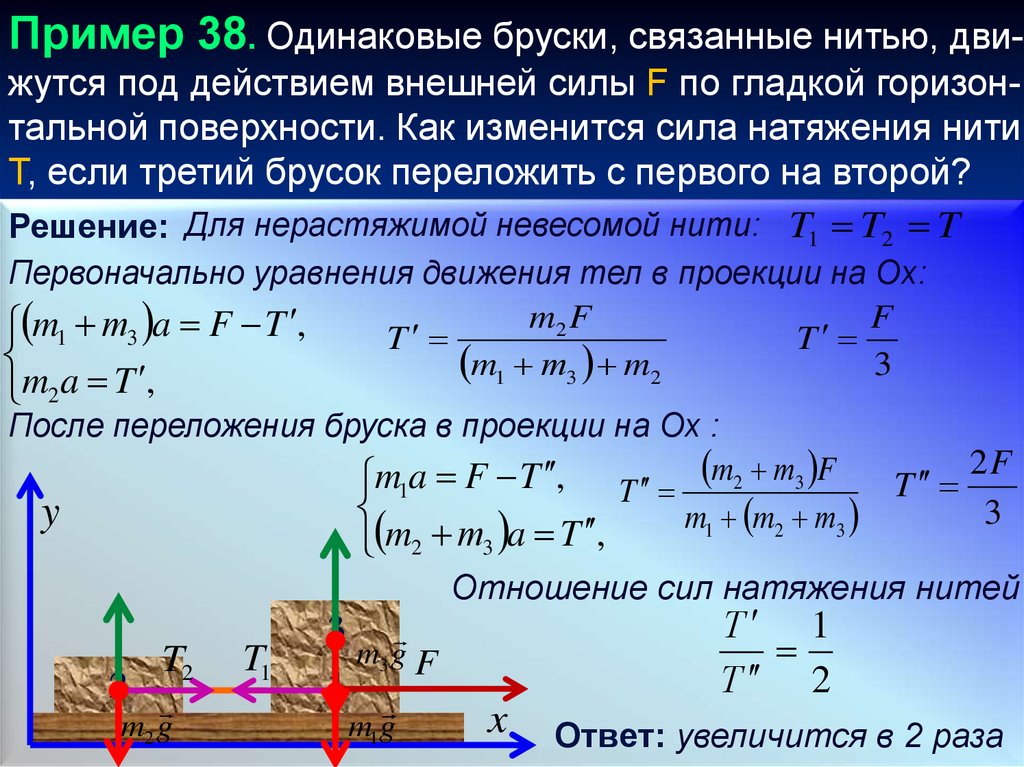
Пример 38. Одинаковые бруски, связанные нитью, движутся под действием внешней силы F по гладкой горизонтальной поверхности. Как изменится сила натяжения нити
T, если третий брусок переложить с первого на второй?
Решение: Для нерастяжимой невесомой нити: T1 T2 T
Первоначально уравнения движения тел в проекции на Ox:
F
m2 F
m1 т3 a F T ,
T
T
m1 т3 m2
3
m2 a T ,
После переложения бруска в проекции на Ox :
m1a F T , T m2 т3 F
y
m1 m2 т3
m2 т3 a T ,
T
2F
3
Отношение сил натяжения нитей
2
T2
m2 g
T1
3
m3 g F
1
m1g
Т 1
Т 2
x
Ответ: увеличится в 2 раза

72. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

1. Момент импульса
L J
М J
2. Момент сил
3. Момент инерции
n
J mi ri
i 1
2
m
J R dm
4. Теорема Штейнера
2
0
J Jc m d 2
Расчет моментов инерции некоторых простых тел

73.

Тело массой т
Ось проходит
через
Прямой тонкий
стержень длиной L
Центр перпендикулярно стержню
Кольцо, обруч, маховик, тонкостенный
цилиндр радиусом R
Сплошной цилиндр
(диск) радиусом R
Центр перпендикулярно плоскости
основания
Середину перпендикулярно плоскости основания
Середину в плоскости основания
Сплошной цилиндр
(диск) радиусом R
Сплошной шар
радиусом R
Центр шара
Полый тонкостенный
шар радиусом R
Центр шара
Рисунок
Момент
инерции
1
2
mL
12
mR
mR
2
2
2
1
mR 2
4
2
2
mR
5
2
2
mR
3

74.

Пример 39. Вал в виде сплошного цилиндра массой
10кг насажен на горизонтальную ось. На цилиндр намотан
невесомый шнур, к свободному концу которого подвешена
гиря массой 2 кг. С каким ускорением будет опускаться
гиря, если ее предоставить самой себе?
Решение: укажем силы Так как нить невесомая, то
Т Т Проведем ось Оу
Равнодействующая сил тяжести mg и натяжения
нити T вызывает равноускоренное движение гири
mg T ma
mg ma T
С другой стороны сила натяжения нити вызывает
у
вращение вала M Tr
Основное уравнение динамики вращательного движения:
1
J
md r 2
Момент инерции вала (цилиндра)
2
Угловое ускорение связано с линейным выражением
M J md r 2 a md
mg ma
a
r
r
22r r
2
Ответ: a 2,8 м / с
r
T
T
mg
а
M J
a r
m
a
g 2,8 м / с 2
m 1 md
2

75.

Пример 40. Через блок в виде диска массой 8 кг, перекинута невесомая нить, к концам которой подвешены грузы массами 10 кг и 20 кг. С каким ускорением будут двигаться грузы? Трением пренебречь.
Решение: Блок имеет массу → сила натяжения нити не одинакова
по всей длине Т1 Т 2
Нить невесома→
Т.к. т2>т1, то ускорения грузов направлены
T1 m1 g m1a
В проекции на Оу
T2 m2 g m2 a
Т1 Т1 , Т 2 Т 2
y
m
d
Блок вращается под действием момента сил
m2 g m2a m1 g m1a r 0,5 md r а
m m
a
g 2,9 м / c
m
2
m 2 m1
1
2
d
2
Т 2
Т1
Т2
а
M T2 Т1 r M m2 g m2a m1 g m1a r
С другой стороны M J Для диска J 0,5 md r 2
a
M 0,5 md r 2 a
r
r
r
Т 1
m1 g
Ответ: 3м/c2
а
m2 g

76.

Сила сопротивления движению тел в
жидкостях и газах
Возникает при движении твердых тел в жидкостях и газах
Трение покоя отсутствует, так как в жидкости (газе) сколь угодно малая
сила может вывести тело из состояния покоя, сообщив ему ускорение
Всегда направлена против движения тела, по касательной к
его поверхности и зависит от скорости движения тела
При небольших скоростях движения (например, в жидкостях)
f тр k1
При больших скоростях движения (например, в газах)
f тр k 2
2
коэффициенты пропорциональности k1 и k2 зависят от формы
и размеров тела, свойств вязкой среды (жидкости или газа) и
температуры