Similar presentations:
Матрицы и определители
1. Матрицы и определители
2. Матрица
Матрица–
это
прямоугольная
таблица
чисел, содержащая m строк
одинаковой длины n
Матрица А называется
матрицей размера mxn,
числа aiJ называются ее
элементами, где i показывает
номер строки, а j – номер
столбца. Числа а11, а22, а33…
образуют главную диагональ
а11
а
А 21
...
а
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
3. Пример
3 5 4 8А 1 1 2 4
3 4 1 2
Размер матрицы – 3х4
Элемент а23=-2
Элемент а31=-3
Элемент а12=5
Главную диагональ
составляют числа
3; -1; 1
4. Классификация матриц
• Две матрицы равны между собой, еслиравны все соответствующие элементы
этих матриц
• Матрица называется квадратной, если
число строк равно числу столбцов. При
этом квадратную матрицу размера nxn
называют матрицей n-го порядка
• Квадратная
матрица
называется
диагональной, если все элементы,
кроме элементов главной диагонали,
равны нулю
b11
b
В 21
...
b
m1
а11 a12
a22
а
А 21
...
...
а
m1 am 2
b12 ... b1n
b22 ... b2 n
... ... ...
bm 2 ... bmn
а11 a12
a22
а
А 21
... ...
а
n1 an 2
а11 0
0 a22
А
... ...
0
0
... a1n
... a2 n
... ...
... amn
aij bij
... a1n
... a2 n
... ...
... ann
0
... 0
... ...
... ann
...
5. Классификация матриц
• Диагональная матрица называетсяединичной, если все элементы
главной диагонали равны единице
• Матрица называется нулевой, если
все элементы равны нулю
• Квадратная матрица называется
треугольной, если все элементы,
расположенные по одну сторону от
главной диагонали, равны нулю
1
0
Е
...
0
0
0
0
...
0
0 ... 0
1 ... 0
... ... ...
0 ... 1
0 ... 0
0 ... 0
... ... ...
0 ... 0
а11 a12
0 a22
А
... ...
0
0
... a1n
... a2 n
... ...
... ann
6. Классификация матриц
• Матрица называется вектором, если онасодержит или одну строку, или один столбец
a
а
• Матрица называется транспонированной
а к a
АС с1
...
...
данной, если каждая строка данной матрицы
а
a
становится столбцом с тем же номером у
новой матрицы. Обозначается Ат
• Матрица называется канонической, если в
начале главной диагонали стоят единицы, а
остальные элементы равны нулю
Т
11
21
12
22
1m
2m
... an1
... an 2
2
... ...
... anm
с
1
0
D
...
0
... сn
0 ... 0
1 ... 0
... ... ...
0 ... 0
7. Пример
1 3А
2 4
Квадратная матрица А
В 1 2 3 Матрица-вектор В
1 0 0
С 2 1 0
3 2 1
Треугольная матрица С
Транспонированные матрицы:
1 2
А
3 4
Т
1
Т
В 2
3
1 2 3
Т
С 0 1 2
0 0 1
8. Действия над матрицами
• Суммой двух матриц одинакового размера называетсяматрица,
полученная
с
помощью
сложения
соответствующих элементов данных матриц
• Произведением матрицы на число называется матрица,
все элементы которой умножены на данное число
• Произведением двух матриц называется матрица, у
которой элемент i-той строки и j-того столбца равен
сумме произведений элементов i-той строки первой
матрицы на соответствующие элементы j-того столбца
второй матрицы
9. Примеры
2 3 0 5 3 14 2 1 7 6 4
2 3 0
( 4)
4 2 1
3 0 1
3 4 5
8 12 0
16 8 4
5 7
2 ( 5) ( 3) 3 0 ( 1) 2 ( 7) ( 3) 6 0 4
2 3 0
3 6
4 2 1 1 4 4 ( 5) ( 2) 3 1 ( 1) 4 ( 7) ( 2) 6 1 4
10 9 0 14 18 0 19 32
20 6 1 28 12 4 27 36
10. Свойства действий
А В В А• Переместительное свойство
• Сочетательные свойства
А В В А
А ( В С ) ( А В) С
( А) А; ( А В) С А ( В С ); ( А В) ( А) В
• Распределительные свойства
А (В С) А В А С
( ) А А А
( А В) А В
• Свойства нуля
А О А
А А 0
• Свойство единицы
Е А А
11. Элементарные преобразования матриц
1. Перестановка местами двух параллельных рядовматрицы
2. Умножение всех элементов ряда матрицы на
число отличное от нуля
3. Прибавление ко всем элементам ряда матрицы
соответствующих элементов параллельного ряда,
умноженных на одно и тоже число.
Две матрицы называются эквивалентными, если
одна из них получается из другой с помощью
элементарных преобразований
12. Пример
2 3 1 2 1 3 2 2 1 3 2 20 2 1 1 1 2 0 1 0 5 2 3
4 0 5 1 5 0 4 1 0 15 6 9
1 3 2 2
0 5 2 3
00 0 0
13. Определитель
Определителем квадратной матрицы называется число,которое вычисляется следующим образом:
1.Если порядок квадратной матрицы равен 1, т.е. она
состоит из 1 числа, то определитель равен этому числу
2.Если порядок квадратной матрицы равен 2, т.е. она
состоит из 4 чисел, то определитель равен разности
произведения
элементов
главной
диагонали
и
произведения элементов побочной диагонали
3.Если порядок квадратной матрицы равен 3, т.е. она
состоит из 9 чисел, то определитель равен сумме
произведений элементов главной диагонали и двух
треугольников параллельных этой диагонали, из которой
вычли сумму произведений элементов побочной диагонали
и двух треугольников параллельных этой диагонали
14. Определитель
1. а11 а112.
а11
а12
а21 а22
а11
а12
3. а21 а22
а31
а32
а11а22 а12а21
а13
а23 а11а22 а33 а12 а23а31 а21а32 а13
а33
а13а22 а31 а21а12 а33 а23а32а11
15. Примеры
3 32 3
5
5
2
1
6
3
1
2 6 ( 3) 5 27
6
0 ( 15 0 48) (6 0 18) 9
4 3
16. Свойства определителей
1.2.
3.
Определитель
не
изменится, если строки
заменить столбцами, а
столбцы – строками
Определитель, имеющий
2
одинаковых
ряда,
равен нулю
Общий множитель какого
–
либо
ряда
определителя
можно
вынести
за
знак
определителя
а b
c d
а b
a b
а
b
nc nd
а
c
b d
0
n
a b
c d
17. Свойства определителей
4.При
перестановке
двух
параллельных рядов определитель
меняет знак на противоположный
5. Если элементы какого-либо ряда
определителя представляют собой
суммы
двух
слагаемых,
то
определитель может быть разложен
на сумму двух соответствующих
определителей
6. Определитель не изменится,
если к элементам одного ряда
прибавить соответствующие элементы
параллельного ряда, умноженные на
любое число
a b
c d
a
b n
c d m
a b
c d
b
a
d
c
a b
c d
a
n
c m
a b na
c d nc
18. Минор элемента определителя и его алгебраическое дополнение
а11 а12А а21 а22
а13
а23
•Минором элемента aIJ
определителя n-го порядка
называется определитель n-1
а31 а32 а33
порядка, полученный из
исходного с помощью
а11 а13
а22 а23
вычеркивания i-той строки и j- М 11
М 32
а21 а23
а32 а33
того столбца
•Алгебраическое дополнение
элемента aIJ определителя –
1 1
А11 ( 1) М11 М11
это его минор, умноженный
на
3 2
А
(
1
)
М 32 М 32
i+j
32
(-1)
19. Свойства определителей
а11 а12 а137. Определитель равен сумме
произведений
элементов А а21 а22 а23 а11 А11 а12 А12 а13 А13
а31 а32 а33
некоторого
ряда
на
а11 а12 а13
соответствующие
им
А а21 а22 а23 а11 А11 а21 А21 а31 А31
алгебраические дополнения
а31 а32 а33
8.
Сумма
произведений
элементов какого-либо ряда
определителя
на
алгебраические
дополнения а А а А а А 0
12 22
13 23
соответствующих
элементов 11 21
параллельного ряда равна нулю
20. Примеры
52
1
5
2
1
3
1
6
1
0
2 0
2 1
0 5
3
6
15 18 42 9
4 3
1 3
1 4
4 3
6
1 4 3
1 4 3
7 6
0 2 1
0 0 7 6
( 147 138) 9
23 21
4 3
5
3
6
0 23 21
3
1
21. Обратная матрица
• Матрица называется невырожденной,если ее определитель не равен нулю, в
противном случае, матрицу называют
вырожденной
• Матрица называется союзной, если она
состоит
из
соответствующих
алгебраических
дополнений
и
транспонирована
• Матрица называется обратной к
данной матрице, если их произведение
равно единичной матрице того же
порядка, что и данная матрица
а11 а12
А а21 а22
а
31 а32
а13
а23
а33
det A 0
А11
*
А А12
А
13
А21
А22
А23
А31
А32
А33
А А 1 А 1 А Е
22. Теорема о существовании обратной матрицы
Любая невырожденная матрица имеет обратную,равную
союзной
матрице,
деленной
на
определитель данной матрицы
А
1
А
det A
*
23. Доказательство теоремы
А А*а11 а12
а21 а22
а
31 а32
а13 А11
а23 А12
а33 А13
а11 А11 а12 А12 а13 А13
а21 А11 а22 А12 а23 А13
а А а А а А
31 11 32 12 33 13
А21
А22
А23
А31
А32
А33
а11 А21 а12 А22 а13 А23
а21 А21 а22 А22 а23 А23
а31 А21 а32 А22 а33 А23
0
0
det A
0
det A
0 det A E
0
0
det A
а11 А31 а12 А32 а13 А33
а21 А31 а22 А32 а23 А33
а31 А31 а32 А32 а33 А33
24. Алгоритм нахождения обратной матрицы
1. Вычислить определитель2. Вычислить
все
алгебраические
дополнения
3. Составить союзную матрицу, не забывая о
транспонировании
4. Разделить
каждое
число
союзной
матрицы на определитель
25. Пример
2 3А
1 1
Пример
1) det A
2
3
1 1
2 ( 3) 5 0
2) А11 1; А12 ( 1) 1;
1 3
3) А
1 2
1 3
1
4) А 5 5
1 2
5 5
*
А21 3;
А22 2
26. Нахождение обратной матрицы 3-го порядка
а11 а12А а21 а22
а
31 а32
а13
а23
а33
а22
а23
1 а21
1
3. А
det A а23
а
21
а
22
1. det A
а11 а21 а31
Т
2. А а12 а22 а32
а
а
а
23
33
13
а32
а33
а31
а12 а32
а13 а33
а11 а31
а33
а31
а32
а13 а33
а11 а31
а12 а32
а12
а13
а11
а13
а11
а12
а22
а23
а21
а23
а21
а22
27. Пример
5 2 1А 3 1 4
6 0 3
Пример
5 2 1
det A 3 1 4 15 48 0 (6 0 18) 9
6 0 3
3
6
5
Т
А 2 1
0
1 4 3
1
4
1 3
1
А
9 4
3
1
0
3
6
3
6
0
2
0
1 3
5 6
1 3
5 6
2 0
2
1
5
1
5
2
1
1
4
3 6 7 3
3
1
5
15 21 23
3
4 9
6 12 11 2
3
3
1
2
3
7
3
4
3
7
9
23
9
11
9
28. Свойства обратной матрицы
1.Определитель обратной матрицыявляется
обратным
к
определителю данной матрицы
2.Обратная
матрица
от
произведения двух матриц равна
произведению матрицы обратной
ко второй на матрицу обратную к
первой
3.Порядок
действий:
транспонирование и нахождение
обратной матрицы можно менять
местами
det A
АВ
1
1
1
det A
1
В А
А А
1 Т
1
Т 1
29. Минор матрицы
а11 a12а21 a22
А
...
...
а
m1 am 2
... a1n
... a2 n
... ...
... amn
Минором матрицы называется определитель, состоящий из
элементов, находящихся на пересечении выделенных k строк и k
столбцов данной матрицы размера mxn
Рангом матрицы называется наибольший порядок того минора
матрицы, который отличен от нуля
Обозначение r(A), rangA
Минор называется базисным, если его порядок определяет ранг
матрицы
30. Пример
2 0 4 0А 3 0 6 0
1 0 30
• Все миноры 3-го
порядка равны нулю
• Минор 2-го порядка,
отличный от нуля:
3
6
1 3
• rangA=2
9 6 15 0








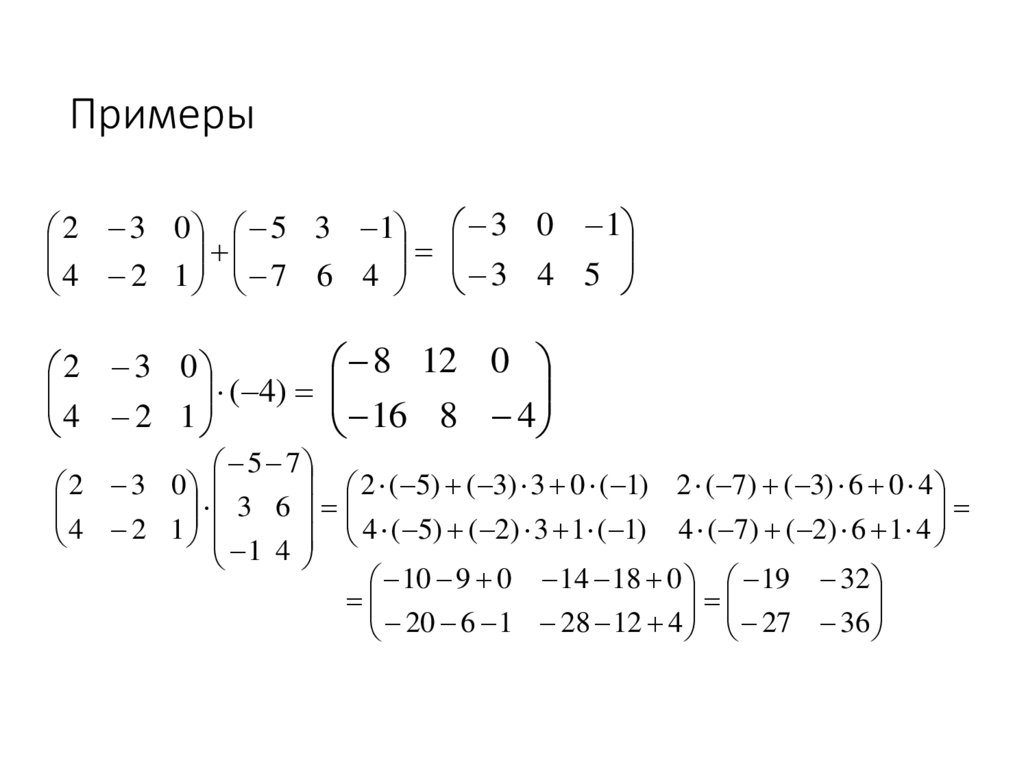




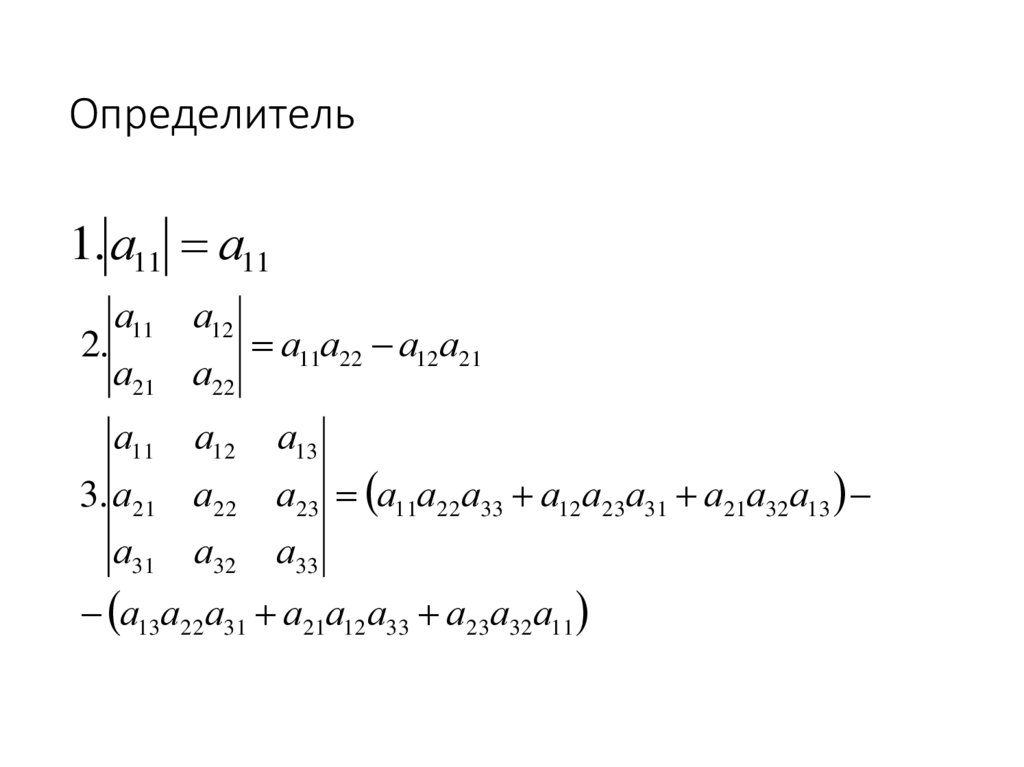
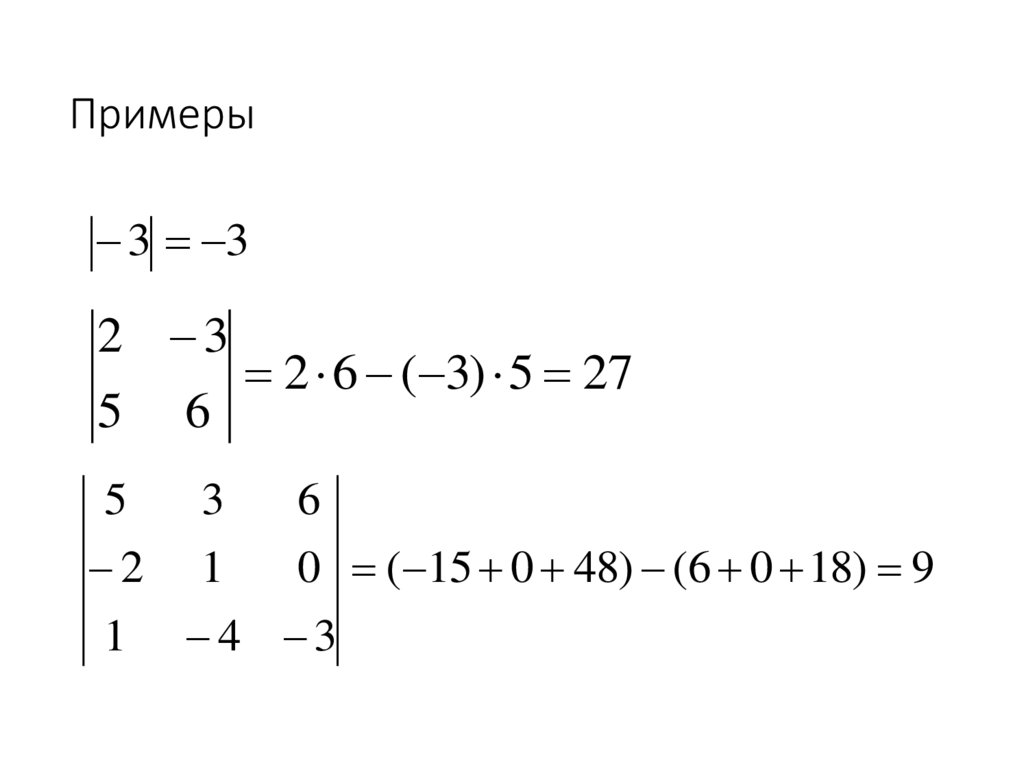




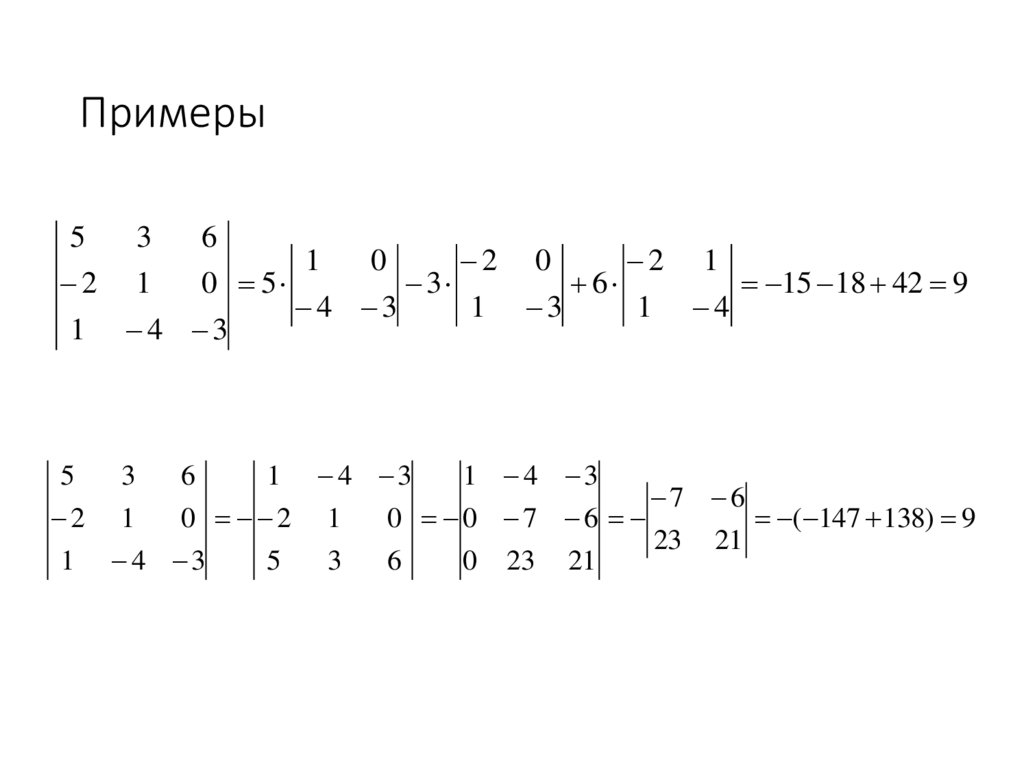




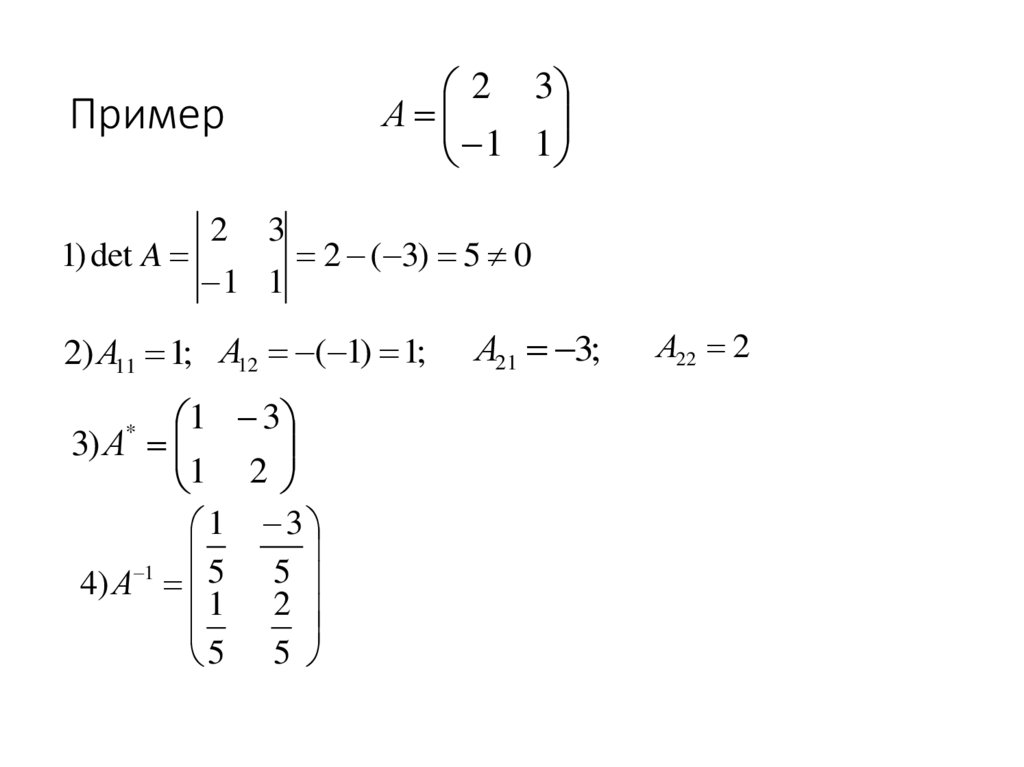





 mathematics
mathematics








