Similar presentations:
Матрицы и определители
1. Высшая математика
1. Линейная и векторная алгебра.2. Аналитическая геометрия на плоскости и
в пространстве.
3. Математический анализ.
4. Теория вероятностей.
5. Математическая статистика.
17.02.2018
лекция №1
1
2. Литература
Натансон И.П. Краткий курс высшейматематики. СПб, 1999, 2000, …, 2009
2. Данко П.Е., Попов А.Г. и др. Высшая
математика в упражнениях и задачах. В
2-х частях М., Высшая школа ,1998 ,
2000, …, 2009
3. Шипачев В. С. Высшая математика. М.,
Высшая школа, 1998 , 2000, …, 2009.
1.
17.02.2018
лекция №1
2
3. Матрицы и определители
1.2.
3.
4.
5.
6.
7.
17.02.2018
Понятие матрицы.
Квадратные матрицы.
Действия с матрицами.
Определители.
Обратная матрица.
Ранг матрицы.
Решение систем линейных
уравнений.
лекция №1
3
4. Понятие матрицы
Определение 1.Таблицу чисел вида
... а1n
а11 а12
... а2 n
а21 а22
А
...... .... ..... .....
а
а
...
а
m2
mn
m1
состоящую из m строк и n столбцов, называют
матрицей.
17.02.2018
лекция №1
4
5. Возможны другие обозначения
а11 а12А=
...
а1п
а21 ... ... а2 п
...
... ... ...
=
а ij
=
a
ij
ат1 ... ... атп
Числа аij называют элементами матрицы
m,n - размерность матрицы
17.02.2018
лекция №1
5
6. Квадратные матрицы
Определение. Матрица называетсяквадратной, если у нее число строк и число
столбцов одинаково
Виды матриц:
1. Элементы квадратной матрицы аij , у
которых номер строки совпадает с
номером столбца, называются
диагональными и образуют главную
диагональ.
2. Квадратная матрица D называется
диагональной , если по главной диагонали
стоят числа отличные от 0 и остальные
элементы равны нулю.
17.02.2018
лекция №1
6
7. Виды матриц:
3. Квадратная матрица Е называетсяединичной , если по главной диагонали
стоят единицы, остальные элементы
равны нулю.
4. Квадратная матрица О называется нульматрицей , если все её элементы равны
нулю.
17.02.2018
лекция №1
7
8. Виды матриц:
5. Диагональная матрица, в которой всеэлементы главной диагонали равны,
называется скалярной.
6. Квадратная матрица элементы которой
расположенные ниже главной
диагонали равны 0, называется
треугольной.
7. Квадратная матрица Аτ называется
транспонированной для матрицы А,
если строки матрицы А являются
столбцами матрицы Аτ .
17.02.2018
лекция №1
8
9. Виды матриц
ВИДЫ МАТРИЦ17.02.2018
лекция №1
9
10. Действия с матрицами
1.При умножении числа на матрицу это числоумножается на каждый элемент матрицы
2.При сложении (вычитании) матриц одинакового
размера соответствующие элементы матриц
складываются(вычитаются)
3. Произведением матрицы А m,n на матрицу B n,k
называется матрица C = AB размера (m, k) ,
элемент которой, стоящий на пересечении i-й
строки и j-го столбца, равен сумме произведений
элементов i-й строки матрицы A на
соответствующие элементы j-го столбца матрицы
B.
17.02.2018
лекция №1
10
11. Примеры
23 1
2
1.
2.
2
1
2
17.02.2018
3
3
5
3 4
3
5
6
4 3
0 6
4
1
4 3
0 5
9
9
15
2 2
1
1
лекция №1
12
0
12
3
2 4
1 3
1 2
2
6
6
1
11
12. Примеры
3.2
1
2
3
3
5
1
4 3
0 5
4
2 1 3 3 4
1 1 3 3 4
2 1 5 3 0
2
1
1
2
2
1
5 4 3 4
5
5
2 3 4
4 5 0
4 6 4
2 6 4
4 10 0
27 11 6
30 5 12
17 1 14
17.02.2018
лекция №1
12
13. Примеры
2A 1
2
AB = ?
17.02.2018
3
3
5
2 1 0
B 0 3 1
2 0 3
4
0
4
4 11 15
AB 10 8 15
4 13
5
лекция №1
13
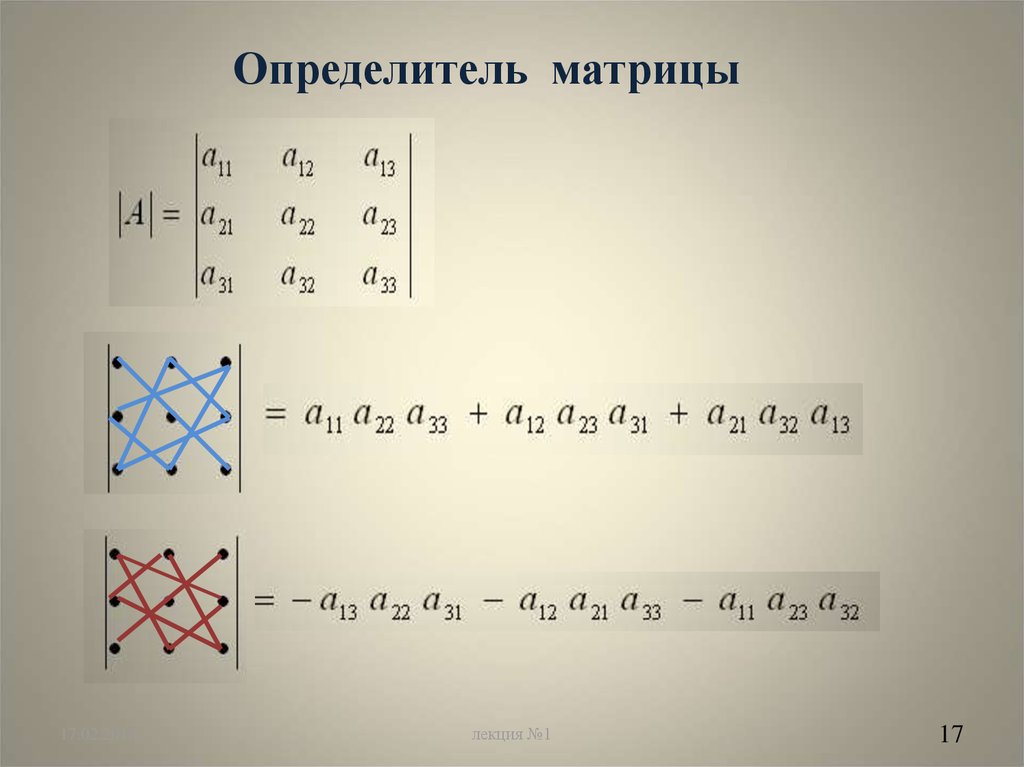
14. Определители
Определение. Определителем илидетерминантом 2-го порядка называется
число
17.02.2018
лекция №1
14
15.
Определение.Определителем или детерминантом 3-го
порядка называется число
17.02.2018
лекция №1
15
16.
17.02.2018лекция №1
16
17. Определитель матрицы
17.02.2018лекция №1
17
18.
17.02.2018лекция №1
18
19. Свойства определителей
1.2.
3.
4.
5.
6.
Если все элементы какой-либо строки или столбца равны
нулю, определитель равен нулю
Если элементы двух строк или столбцов равны или
пропорциональны, определитель равен нулю
При транспонировании величина определителя не
меняется.
Если к элементам одной строки прибавить умноженные
на одно и тоже не равное нулю число элементы другой
строки, величина определителя не изменится.
При перестановке строк или столбцов местами
определитель меняет знак.
Если элементы какой-либо строки или столбца умножить
на одно и то же число. То определитель умножится на
это число.
17.02.2018
лекция №1
19
20. Миноры. Алгебраические дополнения.
Минором Мij элемента аij матрицы Аназывается определитель, полученный
вычеркиванием i-й строки и j-го столбца в
матрице А.
Алгебраическим дополнением элемента
аij называется ее минор, взятый со знаком
(-1)i+j
17.02.2018
лекция №1
20
21. Пример
• Записать минор элемента17.02.2018
лекция №1
a
23
матрицы А
21
22. Пример
• Записать алгебраическое дополнениеэлемента a 23
17.02.2018
лекция №1
22
23. Свойства определителей
7. Определитель равен сумме произведенийэлементов ряда матрицы на
соответствующие алгебраические
дополнения.
8. Сумма произведений элементов ряда
матрицы на алгебраические дополнения
соответствующих элементов параллельного
ряда равна нулю.
9. Определитель произведения двух
квадратных матриц равен произведению
определителей этих матриц.
17.02.2018
лекция №1
23
24. Пример. Вычислить определитель матрицы, разложив его по элементам первого столбца
17.02.2018лекция №1
24
25. Алгебраические дополнения
17.02.2018лекция №1
25
26. Алгебраические дополнения
17.02.2018лекция №1
26
27. Обратная матрица
Определение. Матрица А-1 называетсяобратной к квадратной матрице А, если А-1∙
А=А∙ А-1=Е
Квадратная матрица называется
невырожденной, если ее определитель не
равен нулю.
Теорема. Для существования обратной
матрицы необходимо и достаточно, чтобы
исходная матрица была не вырождена.
Теорема. Если обратная матрица существует,
то она единственна.
17.02.2018
лекция №1
27
28. Обратная матрица
17.02.2018лекция №1
28
29. Пример. Найти обратную матрицу
17.02.2018лекция №1
29
30. Ранг матрицы
Определение. Рангом матрицы называется наивысшийпорядок отличных от нуля миноров.
Элементарные преобразования, не изменяющие ранга
матрицы:
1) Изменение порядка строк и столбцов;
2) Умножение элементов одной строки или столбца на
любое не равное нулю число;
3) Сложение строк с предварительным умножением
любой из них на произвольное не равное нулю
число;
4) Отбрасывание нулевой строки или столбца;
5) транспонирование
17.02.2018
лекция №1
30
31. Пример. Найти ранг матрицы
4 1 5 2A 0 3 1 3
4 3 5 4
Пример. Найти ранг матрицы
4 1
0
3
5
4 1
1 0;
1
8 2 10
3
13
r ( A) 2
17.02.2018
лекция №1
31






























 mathematics
mathematics








