Similar presentations:
Элементарные функции и задаваемые ими конформные отображения
1.
Глава 6Элементарные функции и
задаваемые ими конформные
отображения
6.1 Линейная функция
2.
О п ред елен и е. Л и н ей н ой н азы вается ф ун кц и я w az b, гд еa ,b к о м п л ек сн ы е п о сто ян н ы е и a 0 .
О бласть определения D С , ф ункция однолистна, w / a,
следовательно ф ункция аналитична на С .
Э т а ф у н к ц и я у с т а н а в л и в а е т ...? о т о б р а ж е н и е ...? р о д а .
3.
И так, линейная ф ункция устанавливает кон ф орм ноеотображ ение 1 рода с постоянны м коэф ф ици ентом растяж ения
k a и о д и н аковы м углом п ово рота р авн ы м A rg a.
И зучи м п од роб н ее отоб раж ен и е, осущ ествляем ое д ан н ой
ф ункцией. П ри этом совм естим плоскости
совпали их оси координат.
Р ассм отрим сначала частны е случаи.
z
и
w
так, чтобы
4.
1 . П у с т ь а 1 . Ф у н к ц и я п р и м е т в и д2 w
z b. Э та ф ункция
каж дой точке z ставит в соответствие т. w z b.
Т ак как слож ен и е ком п лексн ы х чи сел геом етри чески своди тся
к слож ению векторов, то при отображ ении w z b каж дая т. z
см ещ ается в соответствую щ ую т. w н а векто р b, и зо б р аж аю щ и й
число b.
5.
В ви ду того, что b п остоян н о,вектор сдви га оди н аков для
всех точек плоскости, и м ы
и м еем п реоб разован и е
параллельного п ереноса.
6.
Е с л и п о л о ж и м z x iy , b b1 ib 2 , W U iV , т о р а в е н с т в оU x b1,
2 w z b з а п и ш е т с я в р а в н о с и л ь н о м е м у в и д е 3
V y b2,
ф орм улы параллельн ого п ереноса в декартовы х коорди н атах.
7.
2 . a 1, b 0 .Запи ш ем а в три гон ом етри ческой ф орм е
4
Ф у н к ц и я п р и м е т в и д w c o s i s i n z .
О чеви д н о w z и A rgw A rgz .
П оясн и те ?
a c o s i s in .
8.
С ледовательно, точки z и w находятсяна одинаковом расстоянии от нулевой
точки и аргум ен ты их отли чаю тся н а
один угол .
Т аки м об разо м , отоб раж ен и е осущ ествляем о е
ф ун кц и ей есть вращ ен и е н а угол вокруг
н а ч а л а к о о р д и н а т . Е с л и z x iy , w U iV ,
т о о т о б р а ж е н и е w a z , a 1 з а п и ш е т с я в в и д е :
U x c o s y s in
5 –
V x s in y c o s
декартовы х координатах.
ф орм улы вращ ения в
9.
3 . В э т о м с л у ч а е к о э ф ф и ц и е н т п р и z , т .е . а я в л я е т с ядействительны м полож ительны м числом a k. Ф ункция w kz
ставит в соответствие каж дом у ком плексном у числу z
ком п лексн ое чи сло w такое, что w k z , A rgw A rgz. Э то
зн ачи т, что точки z и w леж ат н а од н ом луч е, и сход ящ ем и з
w
нулевой точки и отнош ение
k.
z
С ледовательно отображ ение является … ?
10.
гом отети ей с цен тром в н улевой точке и коэф ф и ц иен том k.П р и k 1 и м е е м р а с т я ж е н и е , п р и k 1 - с ж а т и е , п р и k 1 то ж д ествен н о е п р ео б р азо ван и е п л о ско сти .
11.
В ернем ся к рассм отрен и ю общ его случая.П о л о ж и м a k c o s i s i n , т о г д а 1 п р и м е т в и д
w k c o s i s in z b . Э т о п р е о б р а з о в а н и е м о ж е т б ы т ь
п олучен о п утем п ослед овательн ого вы п олн ен и я п реоб разован и й :
c o s i s in z – в р а щ е н и е н а у г о л ,
k – гом отети я,
w b – п а р а л л е л ь н ы й п е р е н о с .
12.
У каж ем некоторы е свойства линейной ф ункции1 . Л и н е й н а я ф у н к ц и я w a z b , г д е a 1 .
С охраняет расстояние м еж ду точкам и.
Д оказательство.
П у с т ь z1, z 2 – п р о и зв о л ь н ы е т о ч к и к о м п л е к с н о й п л о с к о с т и ( z )
w 2 w 1 a z 1 b a z 2 b a z 1 z 2 .
Т а к к а к a 1, т о w 2 w 1 z 2 z1 .
13.
2. Л и н ей н ая ф ун кц и я w az b отоб раж ает треугольн и к н аподобны й ем у треугольн и к.
Д оказать сам остоятельн о.
14.
2. Л инейная ф ункция w az b отображ ает окруж ность наокруж ность.
Д оказательство.
Д анн ое свой ство вы текает и з того, что со ставляю щ и е
п р ео б р азо ван и я
в р а щ
ен и е, гом отети я, п араллельн ы й п ерен ос
обладаю т этим свойством .
15.
16 .2 Ф у н к ц и я w
z
1
Ф ун к ц и я w о п р ед ел ен а н а м н о ж естве D C 0 ,
z
о д н о ли стн а н а D , и м еет н а это м м н о ж естве п р ои зво д н ую
1
/
w 2 0. С ледовательно отображ ение, осущ ествляем ое
z
1
ф ун кц и ей w кон ф орм н ое п ервого род а во всех точках
z
п лоскости С за и склю чен и ем z 0.
16.
З а п и ш е м z в т р и г о н о м е т р и ч е с к о й ф о р м е z r c o s i s in .1
Т огда w
r c o s i s in
1
c o s i s in .
r
1
О тсю д а след ует: w , A rgw 2 K .
r
17.
1В в е д е м в с п о м о г а т е л ь н у ю ф у н к ц и ю w c o s i s i n .
r
1
О чеви д н о , A rg 2 K . С лед овательн о точки и z
r
находятся на одном луче, вы ходящ ем из нулевой точки, что и z,
а п р о и з в е д е н и е и х м о д у л е й r 1 .
Зн ач и т точки и z взаи м н о и н версн ы отн оси тельн о ед и н и чн ой
окруж ности
z 1 .
18.
П остроение инверсны х точекв случае z 1 осущ ествляется
след ую щ и м об разом : и з т. z
проводим касательную к
единичной окруж ности и из
точки касания опускаем
п ер п ен д и кул яр н а л уч 0 z.
О снование перпендикуляра
явл яется то ч к о й и н вер сн о й z.
19.
Е с л и z н а х о д и т с я в н у т р и к р у г а z 1 , т .е . z 1 , т о п о с т р о е н и еи н вер сн о й т. п р о и зво д и тся в об р атн о м п о ряд ке. Т о ч ки
единичной окруж ности при инверсии остаю тся неподвиж ны м и.
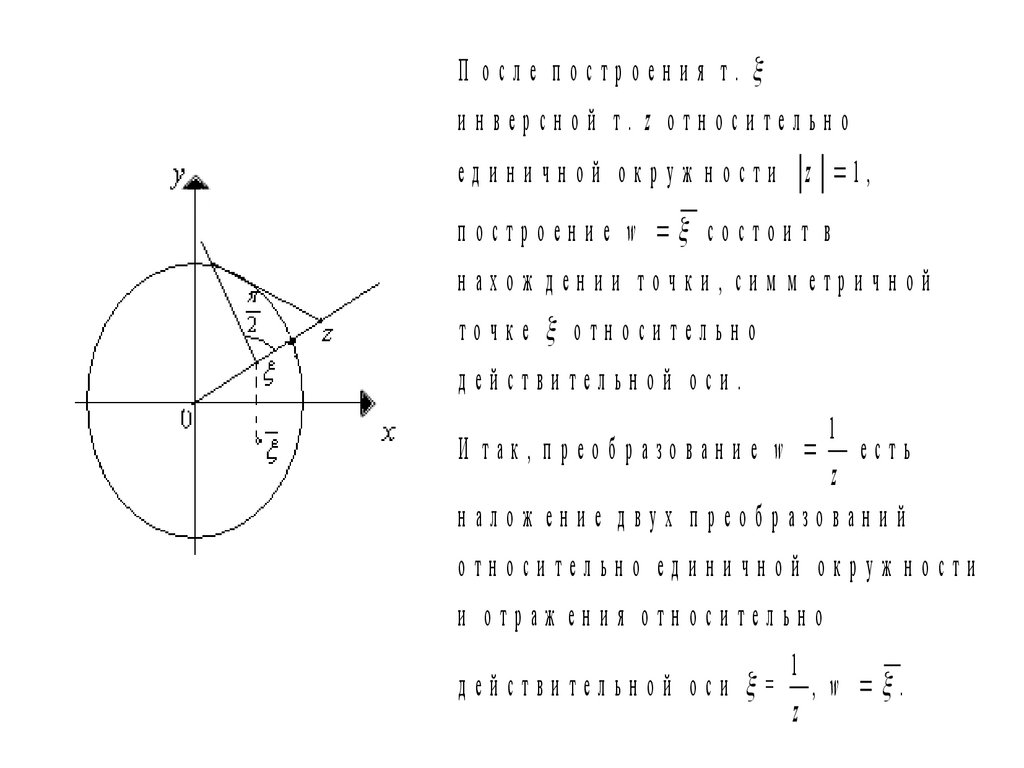
20.
П осле построения т.инверсной т. z относительно
е д и н и ч н о й о к р у ж н о с т и z 1,
п остроен и е w состои т в
нахож дении точки, сим м етричной
точке относительно
действительной оси.
1
И так, п реоб разован и е w есть
z
н алож ен и е д вух п реоб разован и й
относительно единичной окруж ности
и отраж ения относительно
1
д ей стви тел ьн о й о си = , w .
z
21.
1Ф ун кц и я w н е о п р ед ел ен а в т. z 0 и z . Д о о п р ед ел и м
z
эту ф ункцию полож ив в т. z 0 w , а в т. z w 0. Т еперь
эта ф ункция определена на расш иренной ком плексной
плоскости С .
Э то отображ ение конф орм но на С , если условиться считать,
что угол м еж ду кривы м и в бескон ечн о удал ен н ой точке равен
углу м еж д у об разам и кри вы х в н ачале коор д и н ат.
22.
1К руговое свой ство отоб раж ен и я w .
z
1
Д о каж ем , ч то ф ун кц и я w п р ео б р азует п р ям ую в о кр уж н о сть
z
и ли в п рям ую и п реоб разует окруж н ость в окруж н ость и ли в
прям ую . Е сли считать прям ую окруж ностью бесконечно
1
б о л ьш о го р ад и уса, то м о ж н о сказать, ч то ф ун кц и я w
z
п р ео б р азует о кр уж н о сть в о кр уж н о сть. Э то сво й ство
н азы вается кр уго вы м .
23.
Д л я д о казательства зап и ш ем ур авн ен и е п р о и зво л ьн ойокруж ности в декартовы х координатах:
A x 2 y
2
B x C y
D 0
*
Зам ети м , что п ри А 0 уравн ен и е и зоб раж ает п рям ую , а п ри
D 0 - линию , проходящ ую через т. z 0. И з соотнош ения
1
1
1
U Vi
w находим z
и л и x iy
= 2
откуда
2
z
w
U Vi U V
U
V
x 2
и y 2
.
2
2
U V
U V
24.
П о д с т а в л я я в у р а в н е н и е * э т и з н а ч е н и я х и у , н а х о д и мА В U - C V D (U 2 V 2 ) 0 . М ы п о л у ч и л и у р а в н е н и е
окруж ности в обобщ енном виде.
П ри D 0 это уравн ен и е и зоб раж ает п рям ую .
1
И так, ф ункция w отображ ает прям ую или окруж ность,
z
проходящ ие через т. z 0 в прям ую , а не проходящ ие – в
окруж ность.
25.
6.3 Дробно-линейная функцияО п р е д е л е н и е 1 . Д р о б н о -л и н е й н о й н а зы в а е т с я ф у н к ц и я
az b
, где c 0, ad bc 0.
1 w
cz d
С м ы сл огран ичен и й состои т в том , что:
a
b
1. при c 0, d 0 w z
- ф ункция линейна,
d
d
a
2. при ad bc 0 ф ункция сводится к постоянной w и
c
п реоб разует всю п лоскость в од н у точку.
26.
dД о о п р е д е л и м ф у н к ц и ю 1 в т о ч к а х z
и z , полож ив
c
az b
az b a
d
w lim d
и w lim
.
z c z d
c
c z c z d
c
П ри этих дополнениях ф ункция определена на всей
р а с ш и р е н н о й п л о с к о с т и ( z ).
27.
Ф у н к ц и я о с у щ е с т в л я е т в за и м н о -о д н о зн а ч н о е о т о б р а ж е н и еп л о с к о с т и ( z ) н а п л о с к о с т ь ( w ).
a
К аж дом у w w , w
c
a
а при w и w им еем
c
dw b
соответствует зн ачен и е z
,
cw a
d
a
z , z .
c
c
28.
az bad bc
/
Ф ункция w
и м еет п рои звод н ую w
во всех
2
cz d
c z d
d
точках плоскости (z) кром е z , следовательн о она
c
d
аналитична на всей плоскости (z) кром е z .
c
Т ак как w / z 0, то о то б р аж ен и е, осущ ествляем о е этой
d
ф ункцией ком ф орно во всей плоскости (z) и склю чая т. z .
c
29.
dП окаж ем , что ф ункция конф орм на в т. z
и z . П усть
c
d
1 и 2 д в е к р и в ы е о б р а з у ю щ и е у г о л с в е р ш и н о й в т . z .
c
И х об разы — кри вы е Г 1 и Г 2 п роход ят через т. w . К ак б ы ло
п оказан о ран ее угол м еж д у кри вы м и Г 1 и Г
2
в т. w
п р и н и м ается р авн ы м м еж д у и х о б р азам и Г 1 и Г
2
в нулевой
1
т о ч к е п р и о т о б р а ж е н и и . О ч е в и д н о , ч т о Г 1/ и Г 2/ я в л я ю т с я
w
1
cz d
о б р а з а м и к р и в ы х 1 и 2 п р и о т о б р а ж е н и и
, а это
w
az b
d
отображ ение конф орм но в т. z .
c
30.
dП о э т о м у у г о л м е ж д у 1 и 2 в т . z
р а в е н у г л у м е ж д у Г 1/ и Г
c
в н улевой точке и след овательн о углу м еж д у Г 1 и Г 2 в т. w .
d
И так, отображ ение конф орм но в т. z . К онф орм ность
c
дробн о ли н ей ного отображ ен и я в т. z следует из
a
конф орм н ости обратн ого отображ ен и я в т. w .
c
/
2
31.
bc ad2
a
c
З а п и с а в д р о б н о -л и н е й н у ю ф у н к ц и ю в в и д е w
,
d
c
z
c
зам ечаем , что он а м ож ет б ы ть рассм отрен а как н алож ен и е
d
1
a bc ad
п р е о б р а з о в а н и й 3 z , , w
, т .е .
2
c
c
c
d
d
п араллельн ого п ерен оса в т. , и н верси и с п олю сом в т. ,
c
c
d
отраж ением относительно прям ой, проходящ ей через т. ,
c
п араллельн о дей стви тельн ой оси , и , н акон ец , ли н ей н ого
п реоб разован и я.
32.
У к а ж е м д в а в а ж н ы х с в о й с т в а д р о б н о -л и н е й н о г оп реоб разован и я:
1. К руговое свой ство. К аж д ое и з трех п реоб разован и й
3
о б л а д а е т к р у г о в ы м с в о й с т в о м , п о э т о м у д р о б н о -л и н е й н о е
п реоб разован и е об лад ает эти м свой ством .
Д р о б н о -л и н е й н а я ф у н к ц и я п р е о б р а зу е т о к р у ж н о с т ь и л и п р я м у ю ,
d
проходящ ие через точку z
в прям ую , а не проходящ ие
c
через эту точку – в окруж ность.
П очем у?
33.
dЭ то стан ови тся ясн ы м , если зам ети ть, что т. z
переходит
c
d
в w и образ линии, проходящ ей через т. z не м ож ет
c
бы ть огран и чен н ы м .
34.
2. С им м етрия и ее сохранение.О пределение 2. Т очки z и , располож енны е на радиусе
некоторой окруж н ости С и его продолж ен и и так, что
0 z 0 R , гд е 0 и R об озн ачаю т ц ен тр и рад и ус окруж н ости
С , н азы ваю тся со п р яж ен н ы м и и л и си м м етр и ч н ы м и о тн о си тел ьн о
С . Ц ентр окруж ности С считается сопряж ен ны м с бесконечно
удаленной точкой.
35.
Т е о р е м а . П р о и зв о л ь н о е д р о б н о -л и н е й н о е п р е о б р а зо в а н и епереводит точки z и , сим м етричны е относительно
о кр уж н о сти С ,в т. w и , си м м етр и ч н ы е отн о си тел ьн о о б р аза
С этой окруж ности.















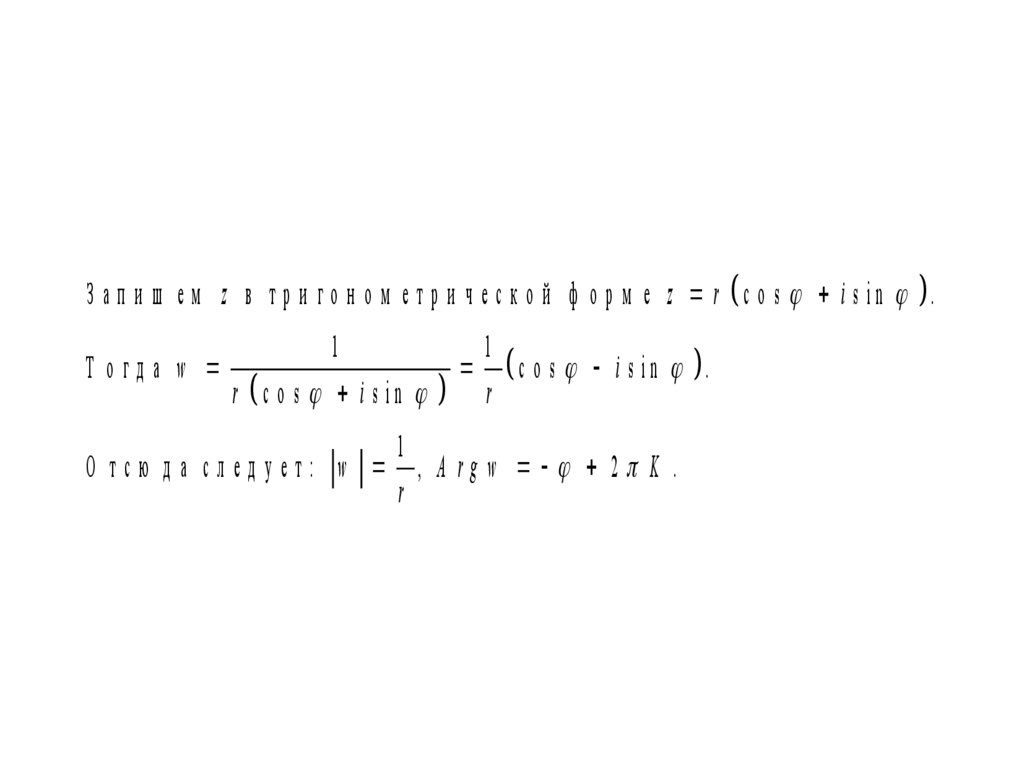








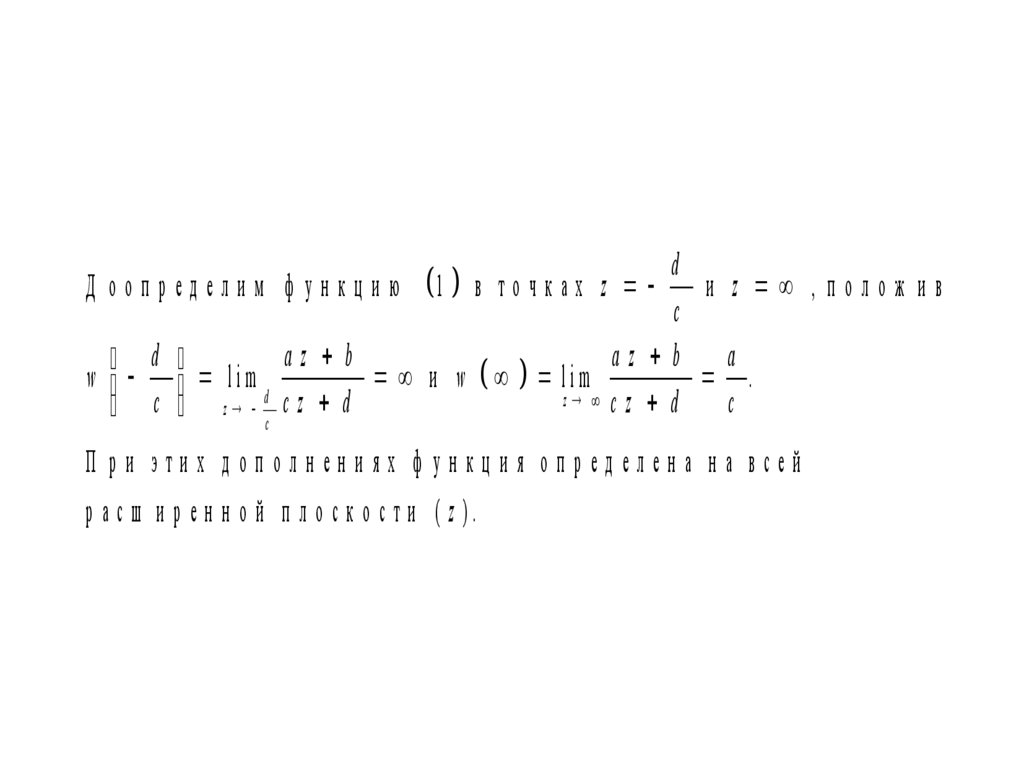



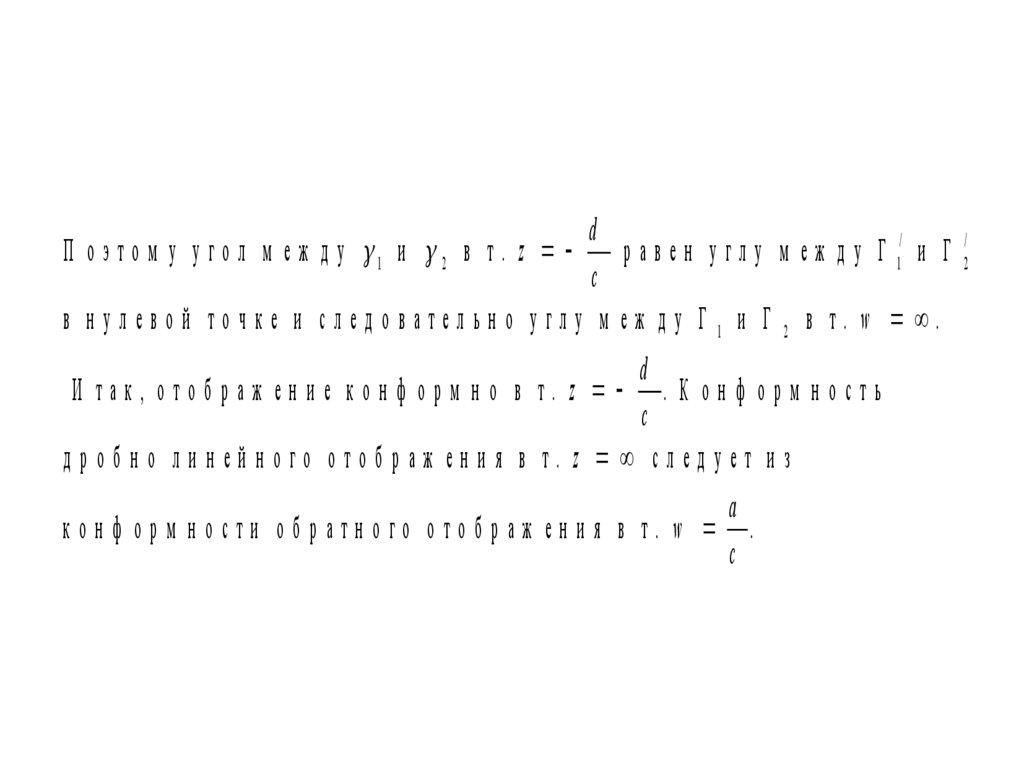






 mathematics
mathematics








