Элементарные функции. Лекция №6

1. Лекция № 6  элементарные Функции

Лекция № 6
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Учебные вопросы
1. Классификация функций.
2. Основные элементарные функции. Их
свойства и графики.

2. Основные элементарные функции: а) степенная: y = xn, nR; б) показательная: y = ax, a>0, a1; в) логарифмическая: y = logax,

Вопрос № 1. Классификация функций
Основные элементарные функции:
а) степенная: y = xn, n R;
б) показательная: y = ax, a>0, a 1;
в) логарифмическая: y = logax, a>0, a 1;
г) тригонометрические: y = sinx, y = cosx,
y = tgx, y = сtgx;
д) обратные тригонометрическим: y = arcsinx,
y = arccosx, y = arctgx, y = arcсtgx.

3. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических операций (сложения, умножения,

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Функции, построенные из основных элементарных
функций с помощью конечного числа
алгебраических операций (сложения, умножения,
вычитания, деления, возведения в целую степень
и извлечения корня) и конечного числа операций
образования сложной функции, называются
элементарными. Пример:

4.

АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
.
Элементарные функции делятся на
алгебраические
и
неалгебраические
(трансцендентные).
Алгебраической называется функция, в
которой над аргументом проводится
конечное число алгебраических действий.

5.

РАЦИОНАЛЬНЫЕ ФУНКЦИИ
.
Алгебраические функции
подразделяются на рациональные и
иррациональные.
Рациональными называются
алгебраические функции, которые не
содержат аргумент под знаком радикала
(корня).

6.

РАЦИОНАЛЬНЫЕ ФУНКЦИИ
.
Рациональные функции разделяются
на целые рациональные функции
(многочлены) и дробные рациональные
(отношение многочленов).
Пример целой рациональной функции:
.
Пример дробно-рациональной функции:
.

7.

Иррациональные функции
.
Иррациональными называются
алгебраические функции, содержащие
аргумент под знаком радикала (корня).
Например,
.

8.

ТРАНСЦЕНДЕНТНЫЕ
ФУНКЦИИ
.
Трансцендентными (неалгебраическими)
называют элементарные функции, которые не
являются алгебраическими. (То есть, они
образованы при помощи возведения в
иррациональную степень, логарифмирования,
с использованием тригонометрических и
обратных тригонометрических операций).
x 1 3 2
y (
)
,
5x 7

9.

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
.
Замечание. Если вид элементарной
функции можно упростить на всей области
определения, то классификации подлежит
именно упрощенная функция.
Например,
- не иррациональная
рациональная, так как
функция,
а

10.

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
.
Трансцендентные
(неалгебраические)
Алгебраические
Рациональные
Дробные
Целые
рациона- рациональные
льные
Иррациональные
.

11.

Вопрос № 2. Основные элементарные функции. Их
.
свойства и графики.
1. Степенные функции
y=xn, n N
y
y
y=x3
y=x2
0
x
0
x
y=x

12.

.
Область определения Х: (– , ).
Область значений Y:
(– , ), если п – нечетно;
0, ), если п – четно.
Нечетная, если п – нечетно;
четная, если п – четно.
Возрастает на (– , ), если п – нечетно;
убывает на (– , 0 и возрастает на (0, ), если
п – четно.
Непериодическая.

13.

.
y=x–n, n N

14.

.
Область определения X: (– , 0) (0, ).
Область значений Y:
(– , 0) (0, ), если п – нечетно;
(0, ), если п – четно.
Нечетная, если п – нечетно;
четная, если п – четно.
Убывает на (– , 0) и на (0, ), если п – нечетно;
возрастает на (– , 0) и убывает на (0, ), если
п – четно.
Непериодическая.

15.

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
.
y х , n N, n>1
n

16.

.
Область определения X:
(– , ), если п – нечетно;
0, ), если п – четно.
Область значений Y:
(– , ), если п – нечетно;
0, ), если п – четно.
Нечетная, если п – нечетно;
общего вида, если п – четно.
Возрастает на (– , ), если п – нечетно;
возрастает на (0, ), если п – четно.
Непериодическая.

17.

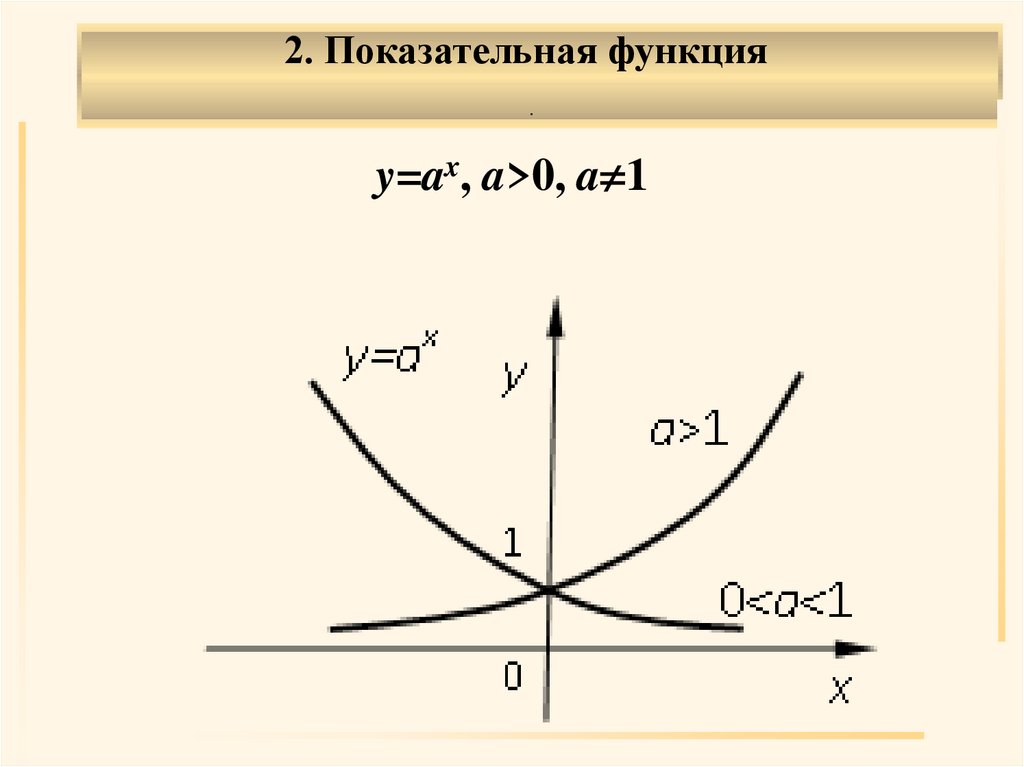
2. Показательная функция
.
y=ax, a>0, a 1

18.

.
Область определения X: (– , ).
Область значений Y: (0, ).
Общего вида.
Возрастает на (– , ), если a>1;
убывает на (0, ), если 0<a<1.
Непериодическая.

19.

3. Логарифмическая функция
.
y=logax, a>0, a 1

20.

.
Область определения X: (0, ).
Область значений Y: (– , ).
Общего вида.
Возрастает на (0, ), если a>1;
убывает на (0, ), если 0<a<1.
Непериодическая.

21.

4. Тригонометрические функции
.
у = sinx

22.

.
Область определения X: (– , ).
Область значений Y: –1, 1].
Нечетная.
Возрастает на 2 n, 2 n ;
2
2
убывает на 2 n, 3 2 n , n Z.
2
2
Периодическая, период 2 .

23.

ТРИГОНОМЕТРИЧЕСКАЯ ФУНКЦИЯ
.
y = cosx

24.

.
Область определения X: (– , ).
Область значений Y: –1, 1].
Четная.
Возрастает на 2 n, 2 n ;
убывает на
Период 2 .
2 n, 2 n ,
n Z.

25.

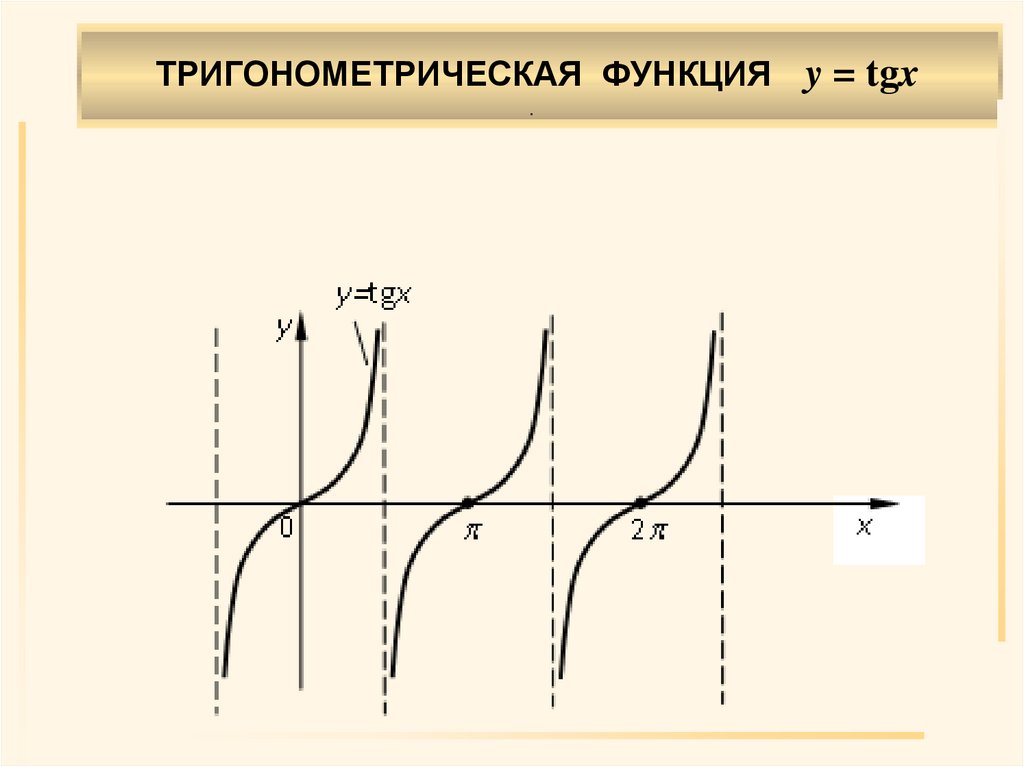
ТРИГОНОМЕТРИЧЕСКАЯ ФУНКЦИЯ y = tgx
.

26.

.
Область определения X: n, n
2
2
n Z.
Область значений Y: (– , ).
Нечетная.
,
Возрастает на n, n n Z.
2
2
Период .
,

27.

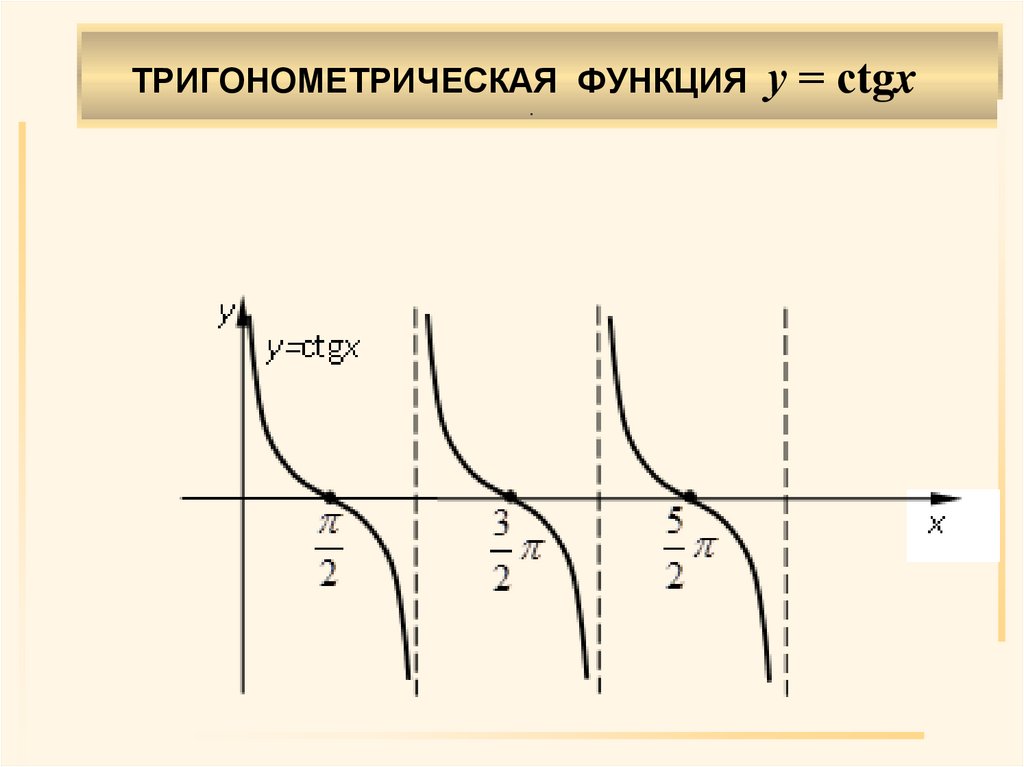
ТРИГОНОМЕТРИЧЕСКАЯ ФУНКЦИЯ у = сtgx
.

28.

.
Область определения X: n, n , n Z.
Область значений Y: – , ).
Нечетная.
Убывает на
Период .
n, n , n Z.

29.

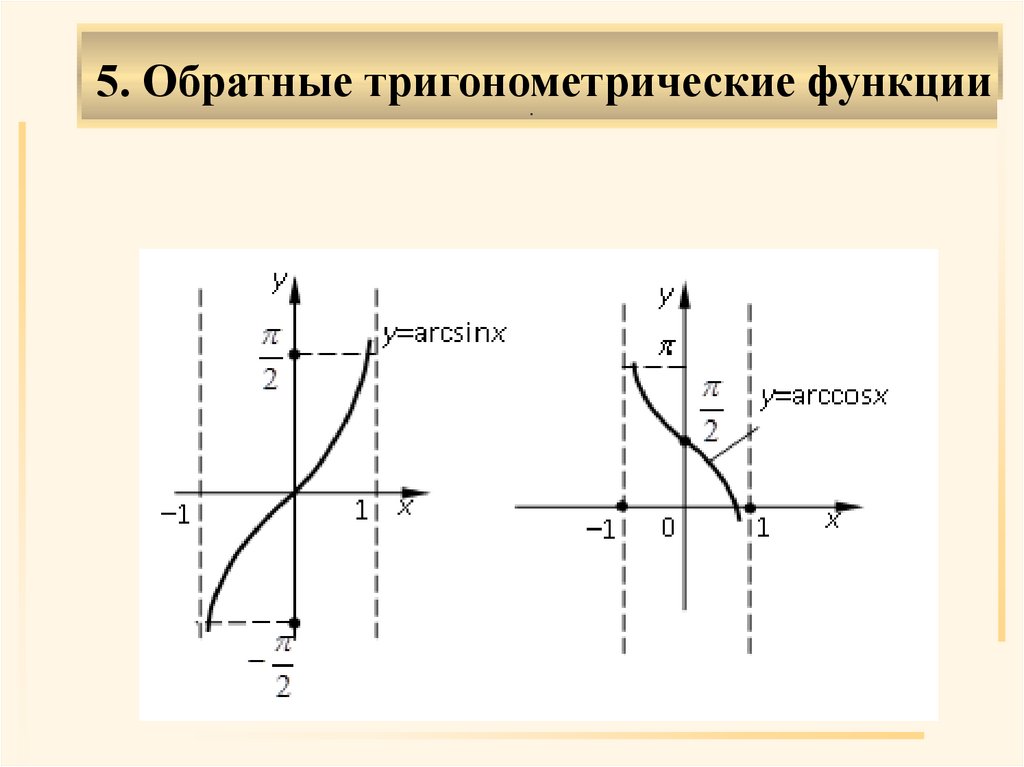
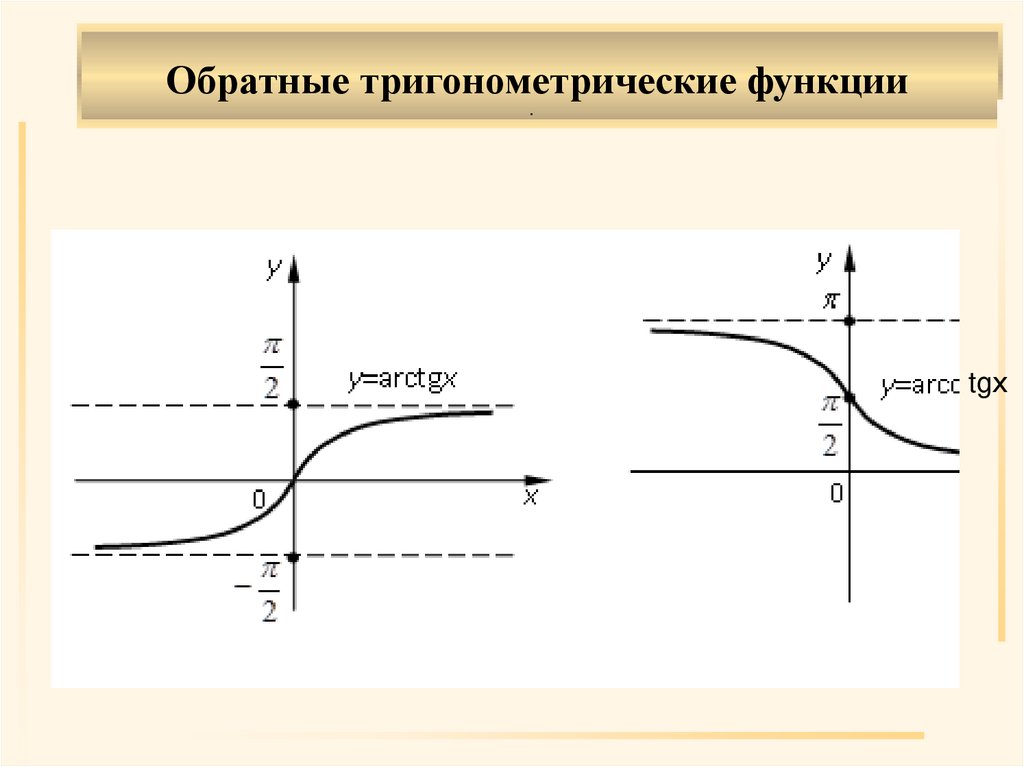
5. Обратные тригонометрические функции
.

30.

Обратные тригонометрические функции
.
tgх

31.

.
Области определения обратных
тригонометрических функций:
y arcsinx , y arccosx
(|x| 1),
y arctgx , y arcctgx
(– <x<+ ).

32. 1. М. Л. Краснов, А. И. Киселев, Г. И. Макаренко, Е. В. Шикин, В. И. Заляпин Вся высшая математика. Том 1. Учебник. (линейная

Литература
1. М. Л. Краснов, А. И. Киселев, Г. И.
Макаренко, Е. В. Шикин, В. И. Заляпин
Вся высшая математика. Том 1. Учебник.
(линейная алгебра и аналитическая
геометрия, введение в математический
анализ). - М.: Едиториал УРСС, 2012 – с.
213-214; 311-317.