Similar presentations:
Основные элементарные функции
1.
Основныеэлементарные
функции
2.
Степенная функция у = х pСвойства и графики степенных
функций вида у = х p существенно
зависят от показателя степени р.
Выбери функцию, свойства и график
которой нужно посмотреть или посмотри
все графики по порядку, щелкнув здесь:
у х2 n , n N
у х 2 n , n N
у х2 n 1 , n N
у х (2 n 1) , n N
у х р , р Q
у х р , р Q
3.
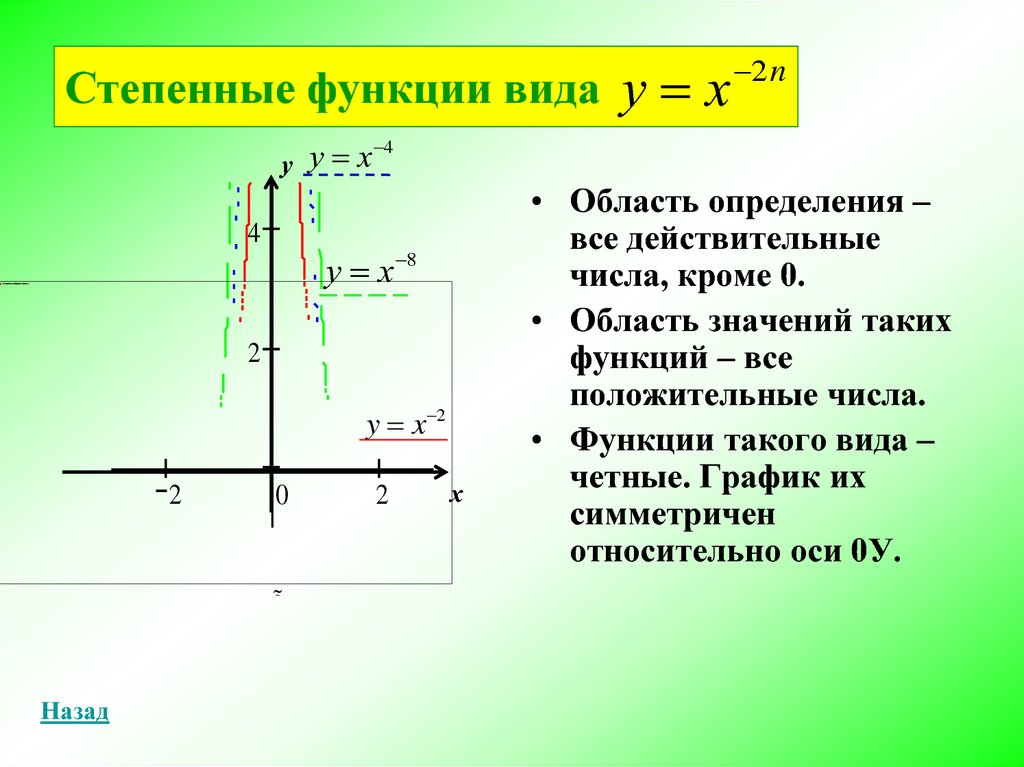
у х 2nСтепенные функци вида
• Областью определения таких
функций являются все
действительные числа.
• Область значений –2 все
õ
положительные числа и
4
число 0.
õ
• Эти функции – четные.
8
õ
График симметричен
относительно оси 0У.
у х4
у
у х8
4
у х2
2
2
0
õ
Назад
2
х
4.
Степенные функции вида у ху
4
2
4
õ
у х 4
у х 8
õ
2
8
y x 2
õ
2
0
õ
Назад
2 n
2
х
• Область определения –
все действительные
числа, кроме 0.
• Область значений таких
функций – все
положительные числа.
• Функции такого вида –
четные. График их
симметричен
относительно оси 0У.
5.
Степенные функции вида у хОбластью определения и
областью значений
степенных функций этого õ3
вида являются все
5
действительные числа
õ
(n – натуральное число)
Эти функции – нечетные. õ9
График их симметричен
относительно начала
координат.
Назад
2 n 1
у
5
у х5
у х3
2
0
у х9
5
õ
2
х
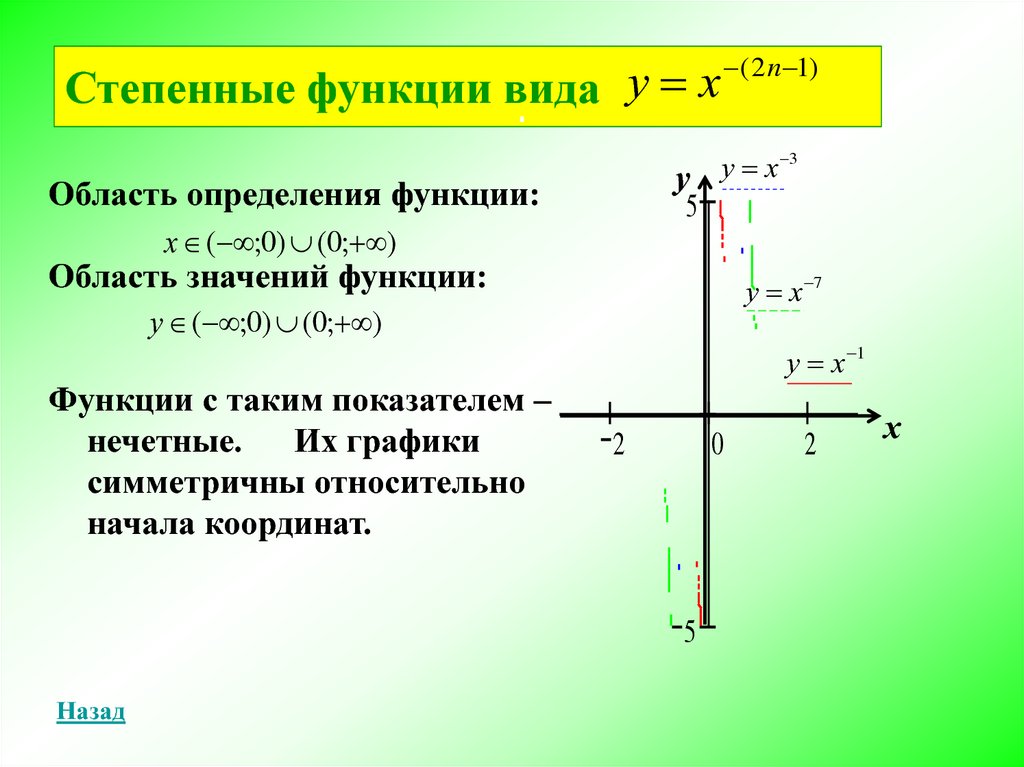
6.
Степенные функции вида у ху х 3
у
5
Область определения функции:
х ( ;0) (0; )
( 2 n 1)
Область значений функции:
у ( ;0) (0; )
у х 7
1
õ
3
Функции с таким показателем
–
õ
нечетные.
Их графики
7
симметричны относительно
õ
начала координат.
у х 1
2
0
5
Назад
õ
2
х
7.
Степенные функции с рациональнымположительным показателем
у
Область определения - все
положительные числа и число 0
у х
у х
3
2
2
2
õ
õ
Область значений функций с таким
1
показателем – также все
1
2
положительные числа и число
õ 0
5
1
у х (у х2 )
Эти функции не являются ни
четными ни нечетными.
0
5
õ
Назад
х
8.
Степенные функции с рациональнымотрицательным показателем
Областью определения и
областью значений таких
функций являются все
положительные числа.
Функции не являются ни
четными ни нечетными.
Такие функции убывают на
всей своей области
определения.
у
у х
4
11
8
1
3
õ
1
3
4
2
õ
у х
0
2
4
õ
Назад
83
х
9.
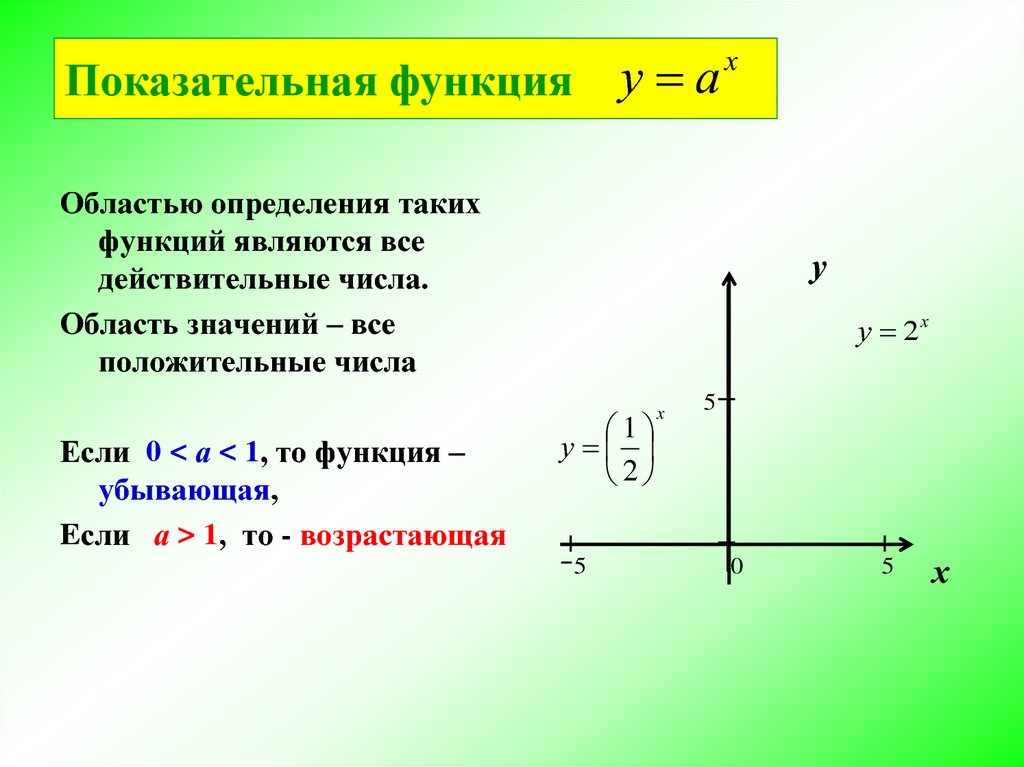
у аПоказательная функция
х
Областью определения таких
функций являются все
действительные числа.
Область значений – все
положительные числа 2õ
1
Если 0 < а < 1, то функция – õ
2
убывающая,
Eсли а > 1, то - возрастающая
у
у 2х
1
у
2
5
х
5
0
õ
5
х
10.
Логарифмическая функция у log a xОбластью определения таких
функций являются все
положительные числа.
Область значений - все
действительные числа. ln( õ)
ln( õ)
Функции – возрастающие,
если а > 1;
убывающие, если 0 < а < 1.
Функции не являются ни
четными ни нечетными.
у
5
у log а x, a 1
0
5
10
х
у log а x, 0 a 1
5
õ
11.
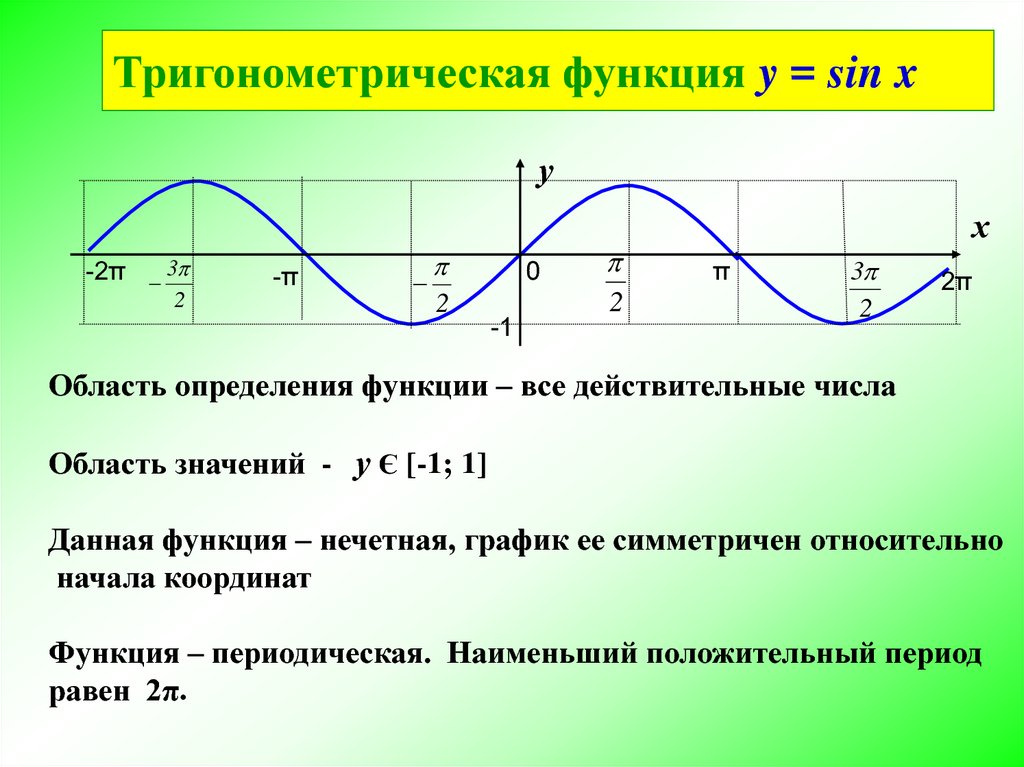
Тригонометрическая функция y = sin xу
-2π 3
2
-π
2
0
-1
2
х
π
3
2
2π
Область определения функции – все действительные числа
Область значений - у Є [-1; 1]
Данная функция – нечетная, график ее симметричен относительно
начала координат
Функция – периодическая. Наименьший положительный период
равен 2π.
12.
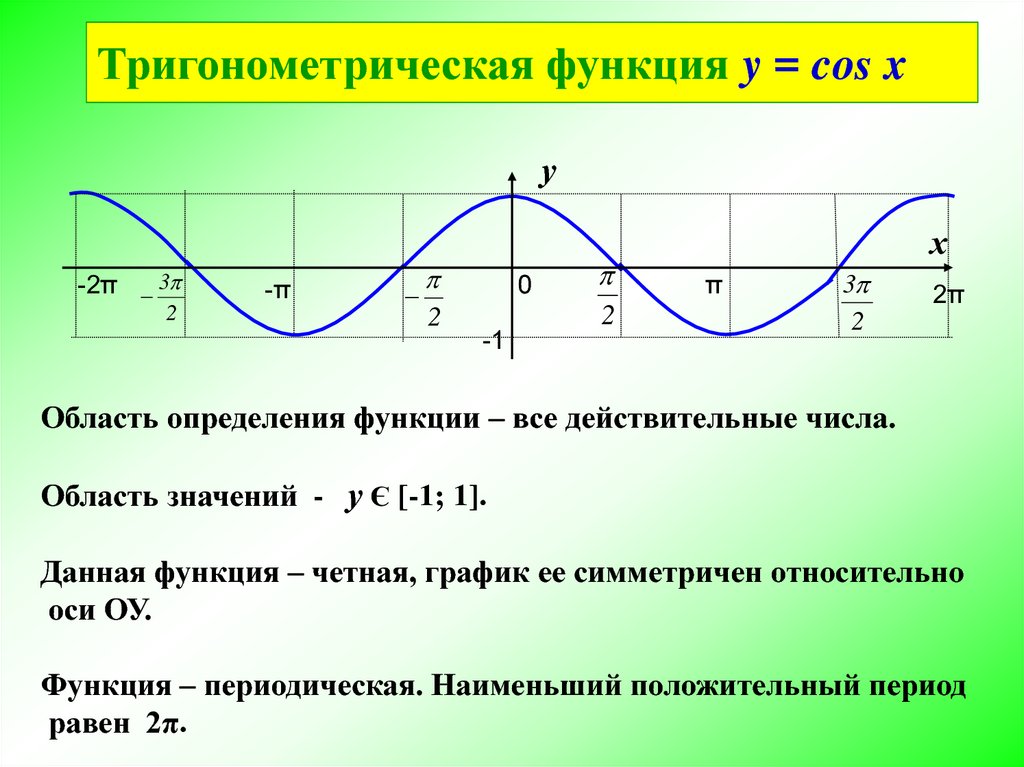
Тригонометрическая функция y = cos xу
-2π 3
2
-π
2
0
-1
2
х
π
3
2
2π
Область определения функции – все действительные числа.
Область значений - у Є [-1; 1].
Данная функция – четная, график ее симметричен относительно
оси ОУ.
Функция – периодическая. Наименьший положительный период
равен 2π.
13.
Тригонометрическая функция y = tg xОбласть определения данной
функции – все действительные
числа, кроме чисел
x
2
у
n ,n Z
1
Область значений функции –
все действительные числа
- 3 ○
2
Функция возрастает на интервалах
(
2
n;
2
-
○
0
2
-1
○
○3
2
2
х
n), n Z
Функция нечетная, график симметричен относительно начала координат.
Функция периодическая, ее наименьший положительный период равен π.
14.
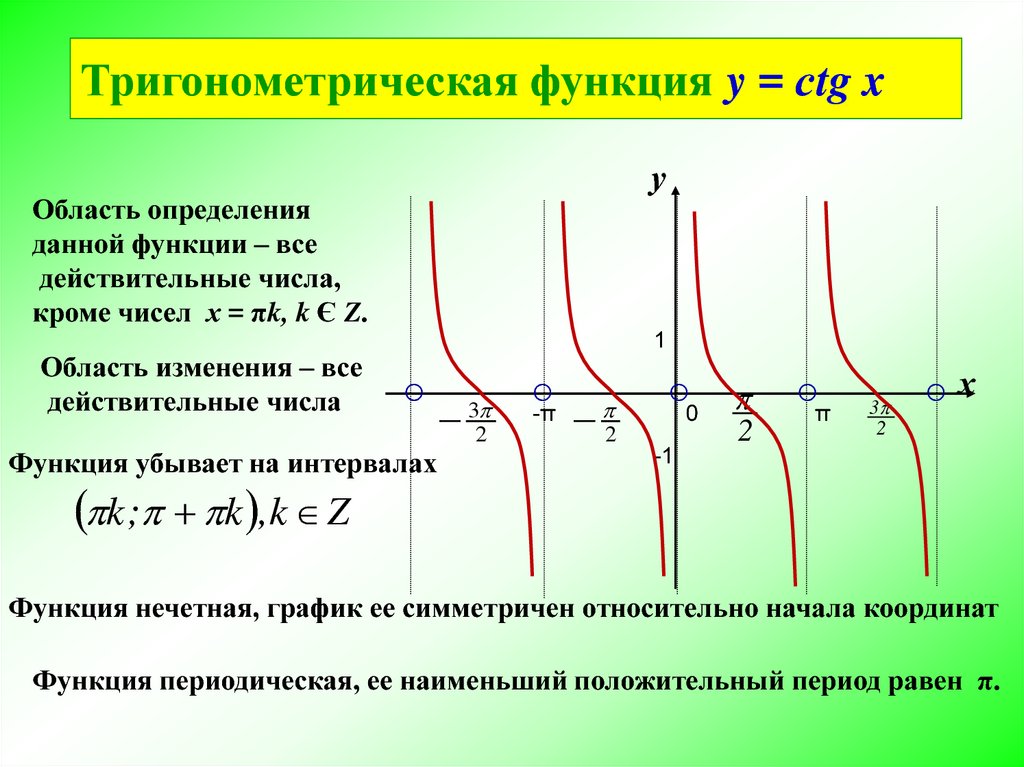
Тригонометрическая функция y = сtg xу
Область определения
данной функции – все
действительные числа,
кроме чисел х = πk, k Є Z.
Область изменения – все
действительные числа
1
○
Функция убывает на интервалах
32
○
-π
2
○0
-1
2
○π
3
2
○х
k ; k ,k Z
Функция нечетная, график ее симметричен относительно начала координат
Функция периодическая, ее наименьший положительный период равен π.








 mathematics
mathematics








