Конформные отображения

1. §20. Конформные отображения.

2.

Определение
z0 w0
обладающее свойствами сохранения
углов и постоянства растяжений
называется конформным
отображением в точке z0
=> б.м. б.м. ;
б.м. б.м. .

3.

Основное определение.
Непрерывное взаимно однозначное
области g Z D W, при котором в
z g выполняются свойства
сохранения углов и постоянства
растяжений, называется конформным
отображением g на D.
K
K
g
D D
g

4.

Теорема 20.1 Если f(z) C (g),
однозначная и однолистная, и f ’(z) 0,
z g, то
K
g D
f z
Доказательство. Данное отображение
f(z) обладает свойствами сохранения
углов и постоянства растяжений
(см. выше).

5.

K
Теорема 20.2(обратная) Если
g D
f z
, то f(z) C (g), однолистна, и f ’(z) 0,
z g.
Доказательство.
K
g D
f z
, то f(z)- непрерывна, однозначна и
однолистна.

6.

Постоянство растяжений =>
w
lim
k 0.
z 0 z
w
Сохранение углов => lim arg .
z
z 0
w
i
f z lim
ke 0.
z 0 z
'
Замечание. Свойство f ’(z) 0, z g
является следствием однолистности.

7.

Теорема 20.3. Необходимым и
достаточным условием конформного
отображения является f(z) C (g),
однозначна и однолистна в g.
Доказательство. Необходимость
доказана выше (Теорема 20.2).
Достаточность. См. "А.Г.Свешников,
А.Н.Тихонов Теория функций
комплексной переменной." М.: НаукаФизматлит 1999, с.156.

8. Основные принципы конформных отображений.

Принцип соответствия границ. Если
f(z) C ( g ), g-односвязна и f( ):
g = D плоскости w с сохранением
направления обхода, то
K
g D
f z

9.

Доказательство. Докажем, что f(z)
однолистна в g, т.е.
а) w1 D ! z1 g : w1=f(z1);
б) w2 D не ни одной z2 g: f(z2)=w2.
Рассмотрим две произвольные точки
w1 D и w2 D и построим в g
вспомогательные функции
F1(z)=f(z)-w1, F2(z)=f(z)-w2 , z g.

10.

Подсчитаем число нулей этих
функций по принципу аргумента:
g
f
g
D
w1
w2
D
0
w1 F1
0
w2 F2

11.

1
N F1 z g Var arg( f w1 ) g 1
2
1
N F2 z g Var arg( f w2 ) g 0
2
Замечание. Если f(z) C ( g\z0), z0полюс первого порядка и f( ): g с
изменением направления обхода, то
K
g E\D
f z

12.

Обратная теорема. Если f(z):
K
g D
f z
(D-ограничена), то f(z) C ( g ) и
осуществляет непрерывное и взаимнооднозначное соответствие границ
g D.

13. Теорема Римана

Основной закон конформных отображений
g Z ; D W
K
g D
f z ?
Теорема Римана. Если g- односвязная
g Z , g состоит более чем из одной
точки, то
K
g D

14.

Теорема 20.4. Если g- односвязная g Z
, g состоит более чем из одной
K
точки, то ! f(z) C (g): g w 1
f z
так что f(z0) = 0 и arg f '(z0)= , z0 g и заданные числа.
Полное доказательство см.
А.В.Бицадзе "Основы теории
аналитических функций".

15. Замечания

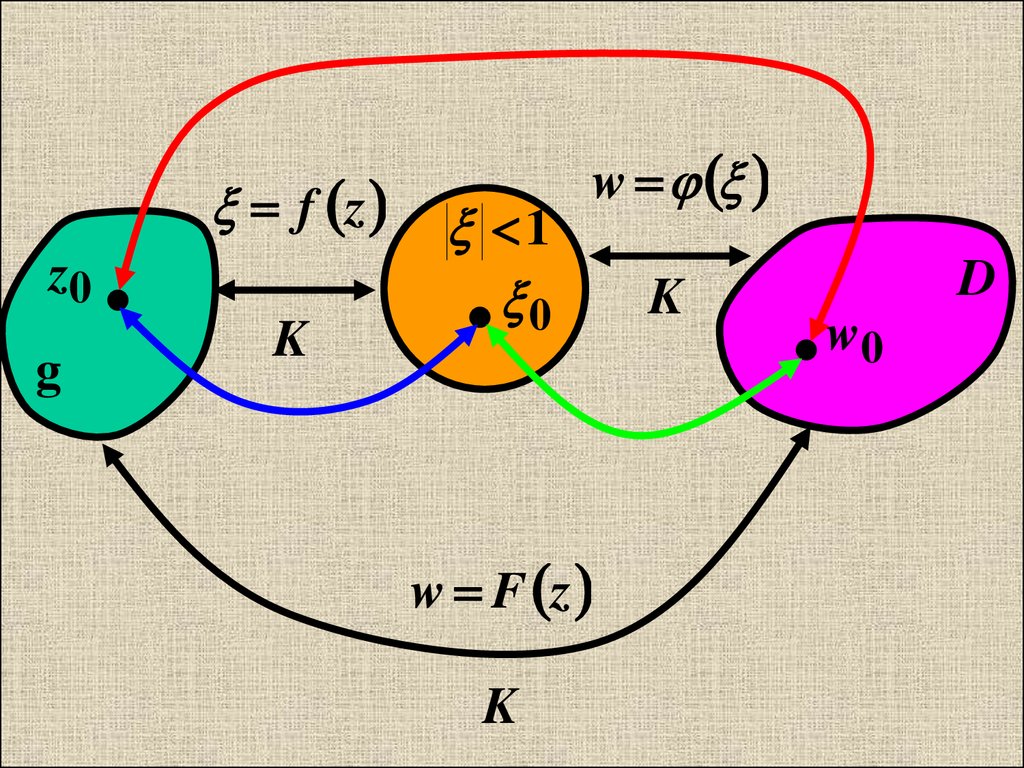
1) Пусть g Z ; D W т. Римана
K
, f(z0)= 0
Тогда =f(z): g 1
f z
K
и w= ( ): 1 D
, ( 0)= w0
K
=> w=F(z)= (f(z)): g D F(z0)=w0
F z

16.

f z
z0
g
K
1
0
w
w F z
K
K
D
w0

17.

2) Односвязность существенна!
3) Условия т. Римана можно заменить
установлением соответствия 3-х точек
g трем точкам D.
1
w1
3
g
2
D
w3
w2

18. п.4. Основные функции, используемые при конформных отображениях.

19.

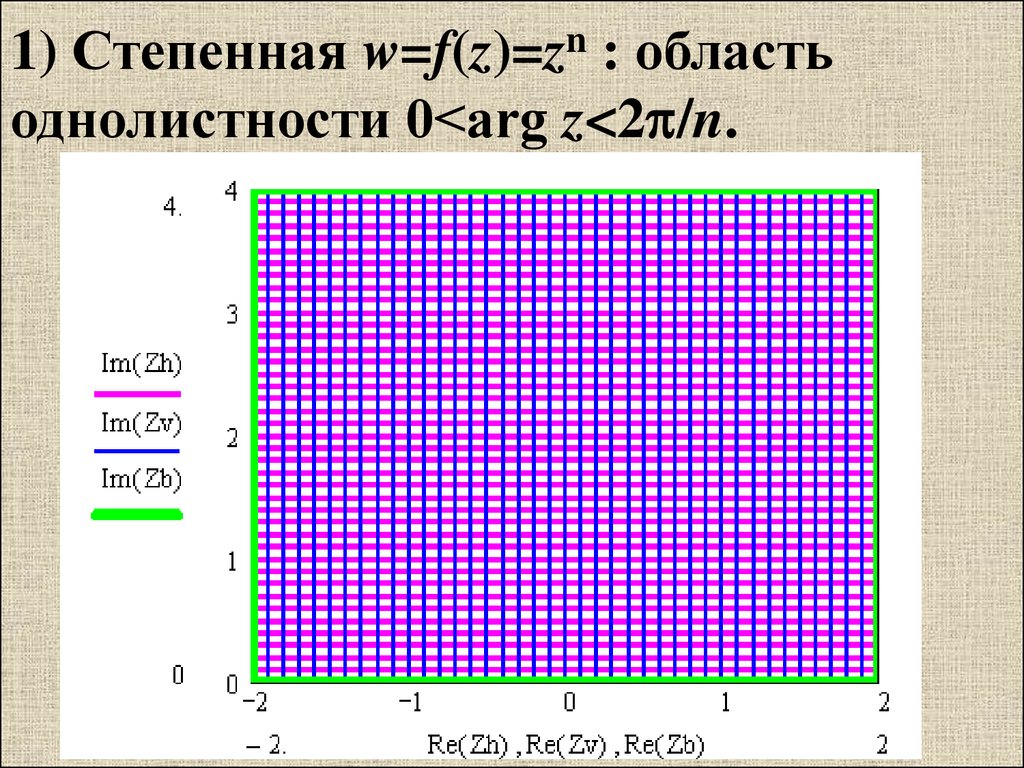
1) Степенная w=f(z)=zn : область
однолистности 0<arg z<2 /n.

20.

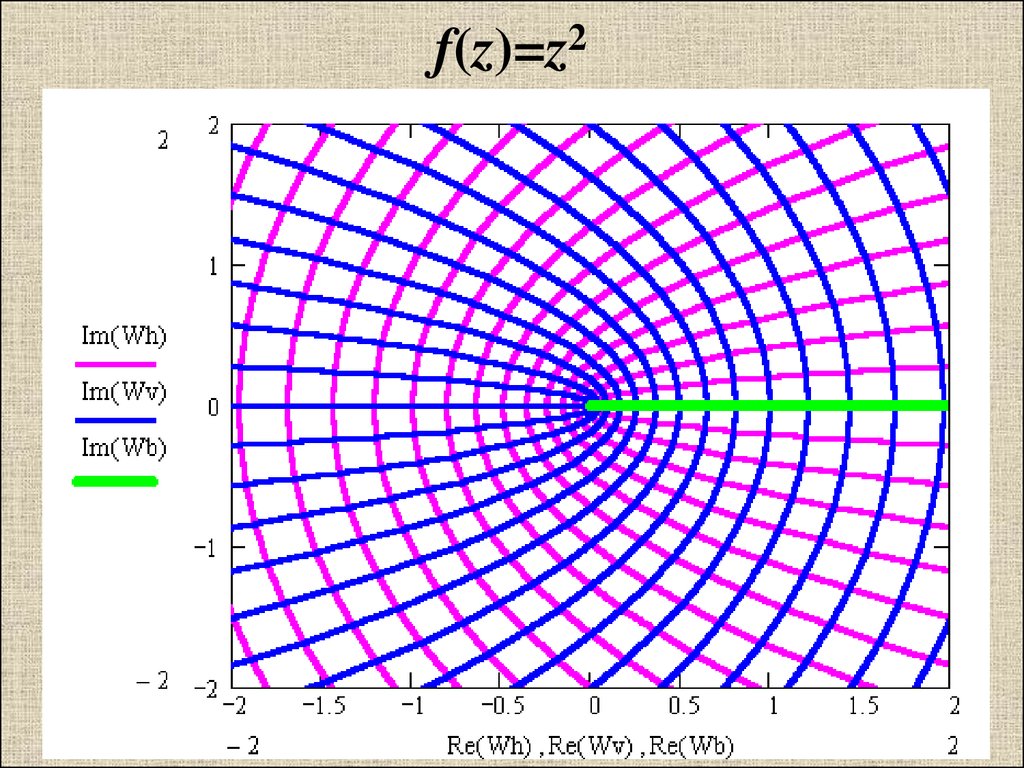
f(z)=z2

21.

22.

23.

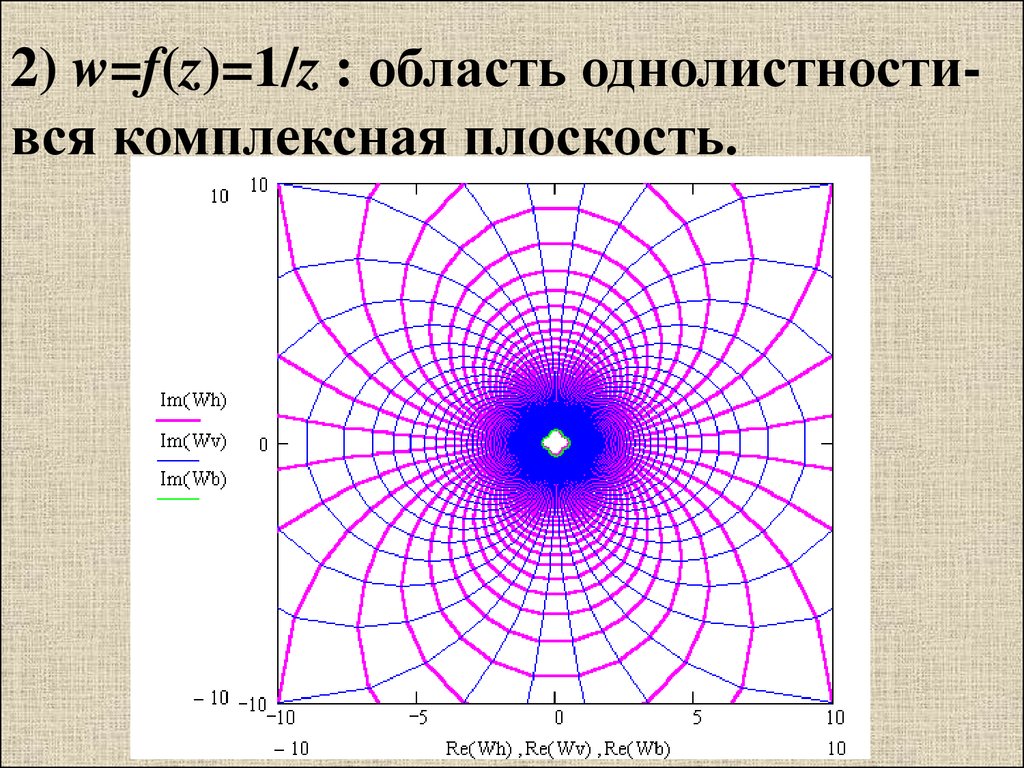
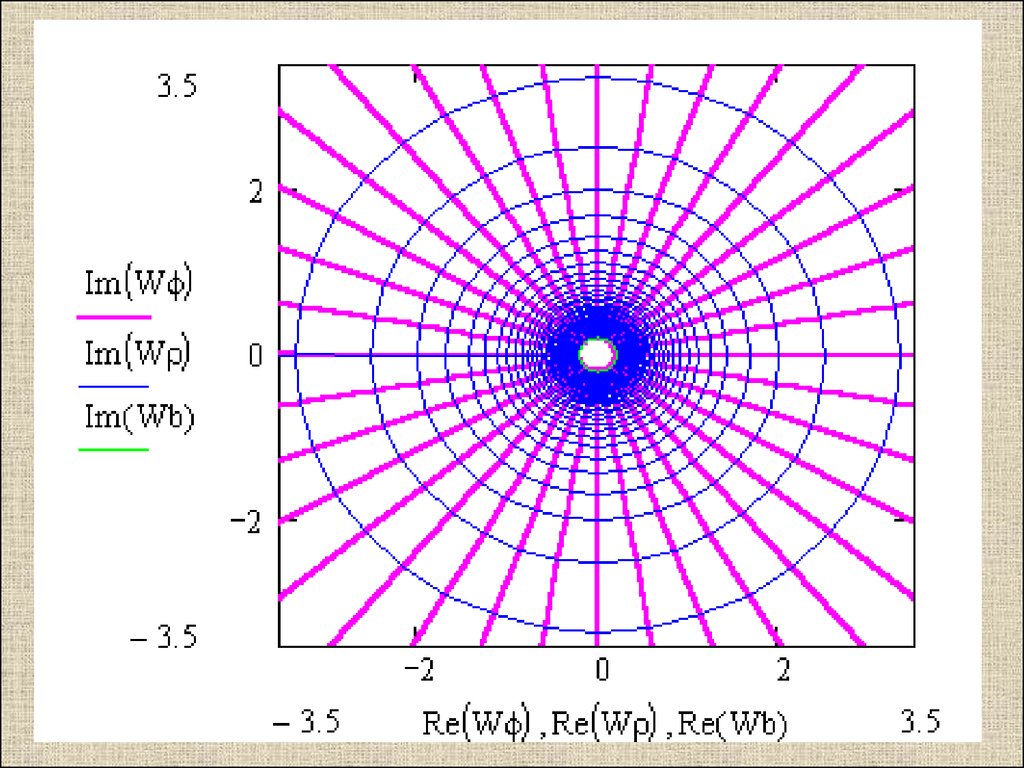
2) w=f(z)=1/z : область однолистностився комплексная плоскость.

24.

25.

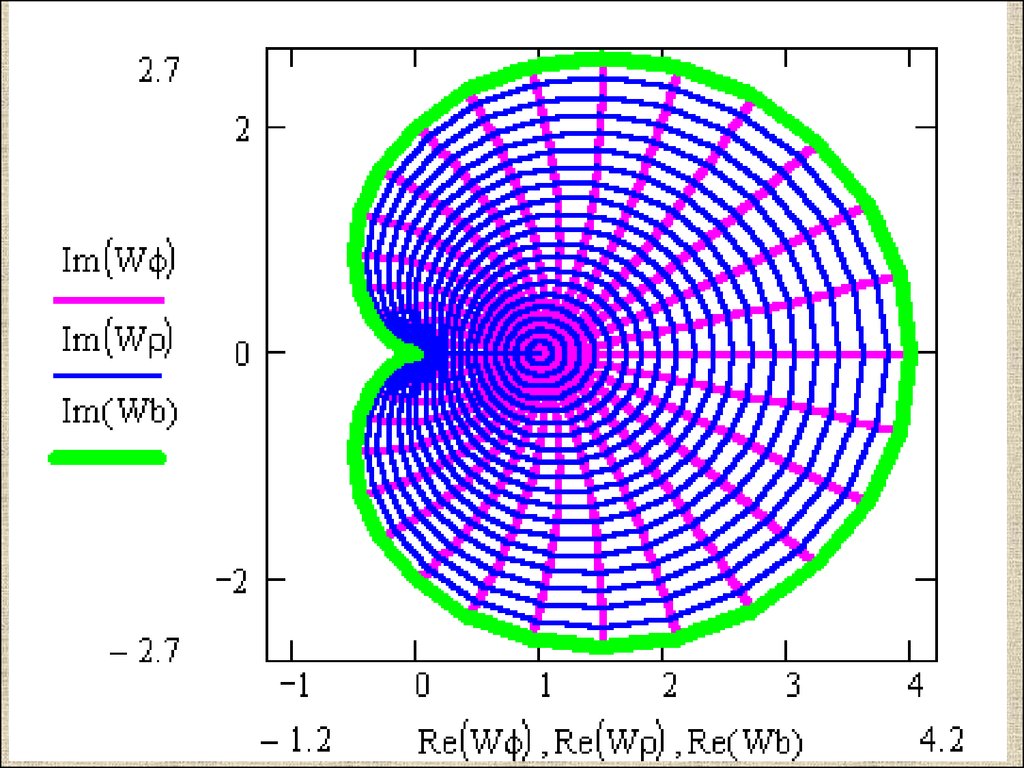
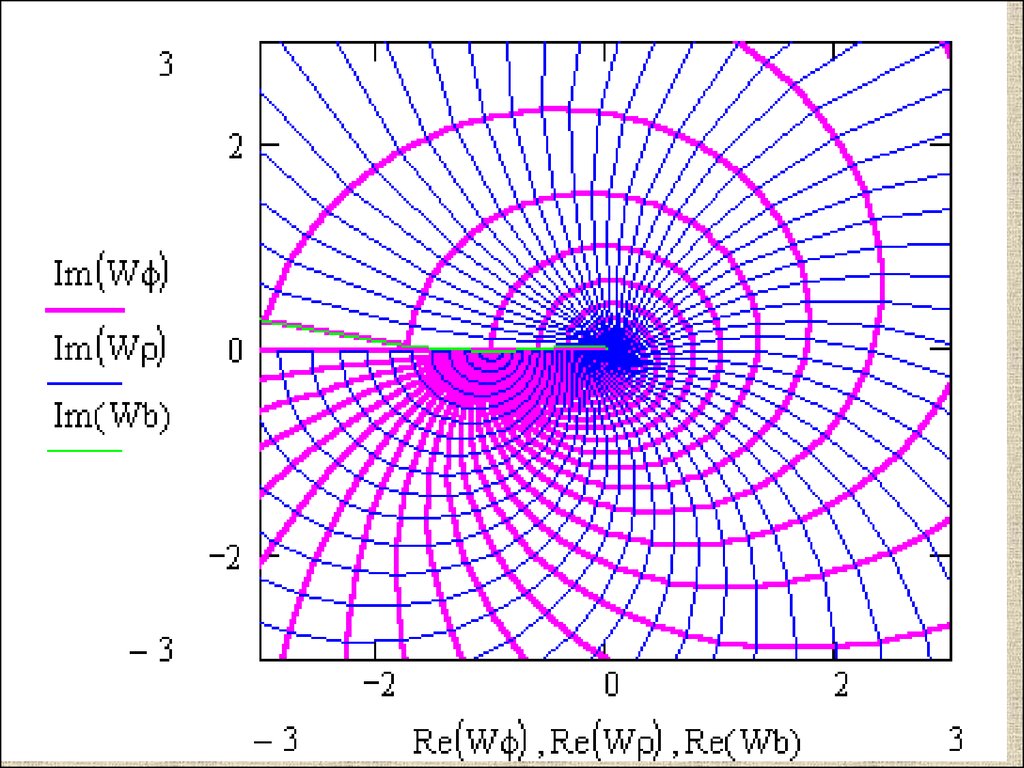
3) w=f(z)=ez : область однолистности <Im z< .

26.

27. Дробно-линейная функция (ДЛФ)

az b
z
w f z
cz d
z
' w
'
z
'
z
K
Z W
3 параметра,
.
, f '(z) 0 для z

28.

1) Геометрический смысл.
f z 1
z
повороты и растяжения, отражение
от действительной оси, инверсия

29.

2) Заданием соответствия z1 w1,
z2 w2, z3 w3, ДЛФ определена
однозначно, т.е. коэффициенты , ,
однозначно выражаются через z1, w1,
z2 , w2, z3 ,w3.

30.

Доказательство
z1
w1
z1
z2
w2
z2
z2 z1
w1 w2
z1 z2
z3
w3
z3
z3 z1
w1 w3
z1 z3
w1 w2
z1 z2 z3
w1 w3
z1 z3 z2

31.

w w2
z z2 z3
w w3
z z3 z2
w w2 z z2
w w3 z z3 w z
z
w1 w2 z1 z2
w1 w3 z1 z3

32. Свойства дробно-линейной функции.

1) Круговое: A(x2+y2)+Bx+Cy+D=0;
z=x+iy=1/ =1/( +i )=
= /( 2+ 2)-i /( 2+ 2)=>
x= /( 2+ 2), y= - /( 2+ 2)
=> A+B -C +D( 2+ 2)=0.

33.

Окружность на плоскости однозначно
определяется заданием 3-х точек.=>
Задав zi wi, i=1,2,3
c сохранением направления обхода
однозначно определим дробнолинейную функцию
K
g D

34.

K
Пример. z 1 Im w 0
f z ?
z=1 w= 0; z= i w= 1; z= -1 w = ;
w= (z-1)/(z+1);
1= (i-1)/(i+1)=> =-i => w=i (1-z)/(1+z).

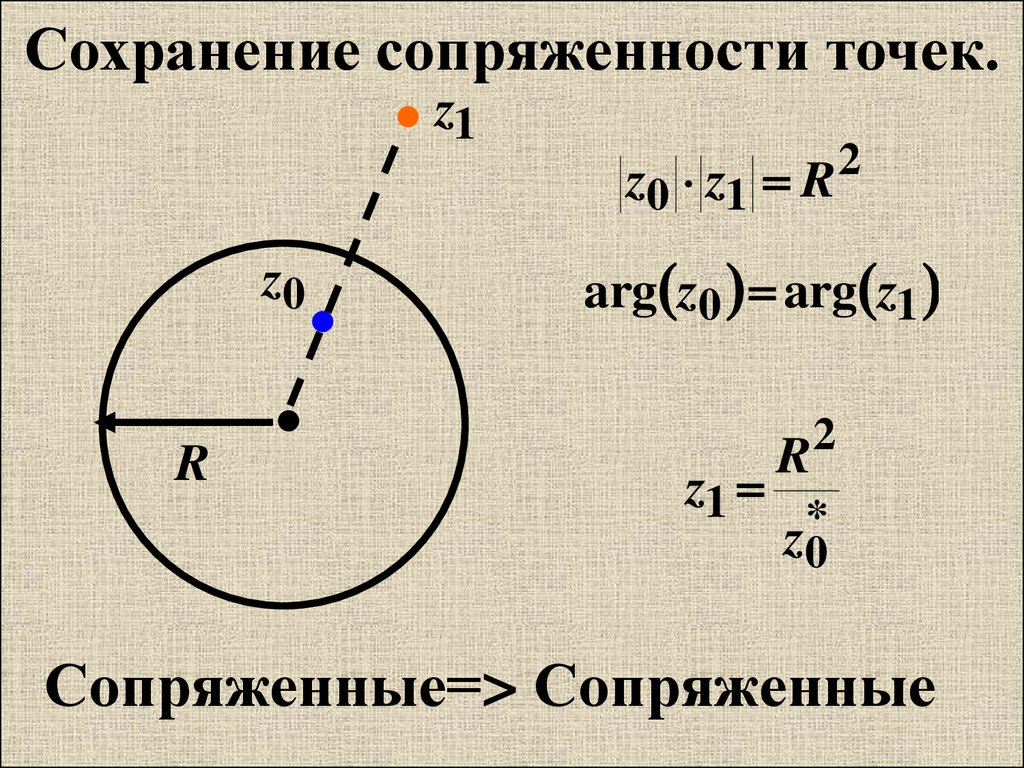
35. Сохранение сопряженности точек.

z1
z0
R
z0 z1 R
2
arg z0 arg z1
z1
R
2
*
z0
Сопряженные=> Сопряженные

36.

K
Пример. Im z 0 w 1
f z ?
w
z z0
*
z z0
Im z 0
z0 w 0 0
, 1
w 1
z0
0
*
z0

37.

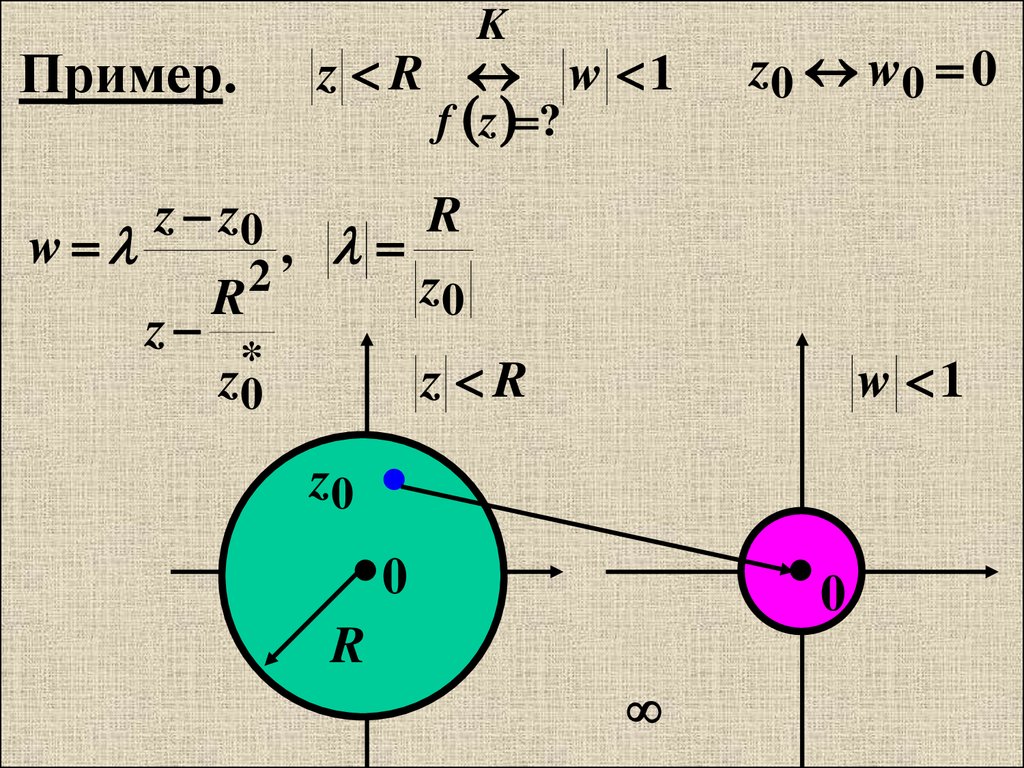
Пример.
w
K
z R w 1
f z ?
z0 w 0 0
z z0
z
R
,
2
z0
R
*
z0
z R
w 1
z0
0
0
R