Similar presentations:
Конформные отображения
1.
Пусть в плоскости z дана точка z0, черезкоторую проведены кривые γ1 и γ2.
Функция w=f(z) - аналитична в некоторой
области, и отображает точку z0 в точку w0
на плоскости w, где w0=f(z0).
Линии γ1 и γ2 отображаются в линии Г1 и Г2,
проходящие через точку w0.
2.
f (z )v
y
0
z0 z
z0
1
1
2
0
2
x
Ф1
Г1
Ф2
Г2
u
3.
Выберем на кривой γ1 точку z0+Δz, котораяотображается в точку w0+Δw на кривой Г1.
Комплексное
число
Δz
изображается
вектором
z0 , z0 z
а число Δw - вектором
0 , 0
Т.к. функция w=f(z) - аналитична в точке z0,
то
f ( z ) lim
z 0 z
4.
Пустьz 0 так, чтобы точка z0+Δz
оставалась на кривой γ1, тогда 0
так, что точка w0+Δw будет перемещаться
по кривой Г1.
Если существует
lim
f ( z )
z 0 z
то будут существовать и пределы
lim
f ( z )
z 0 z
lim Arg
Argf ( z )
z 0
z
5.
ArgArg Arg z
z
где
-
Arg z, Arg
углы,
образованные
векторами,
изображающими числа Δz, Δw с осью х.
Пределы величин ArgΔz и ArgΔw равны,
соответственно, углам φ1 и Ф1.
6.
Argf ( z0 ) Ф1 1Аналогично, если точка z0+Δz стремится к
точке z0 по кривой γ2, то
Argf ( z0 ) Ф2 2
Тогда
Ф1 1 Ф2 2
Ф2 Ф1 2 1
7.
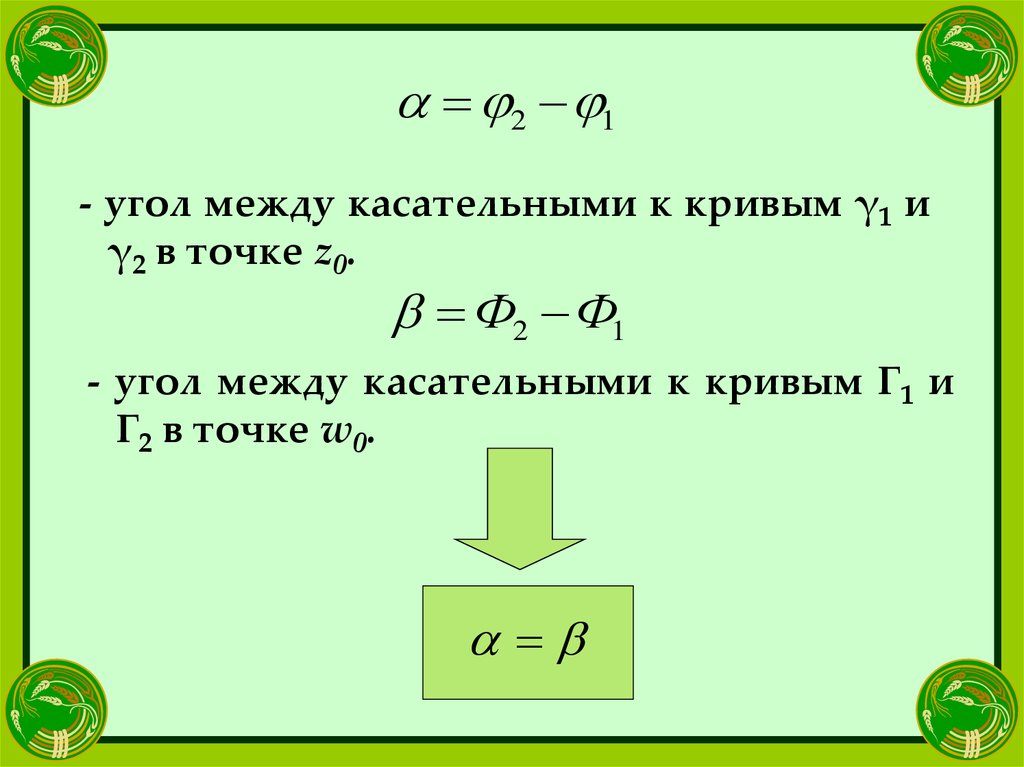
2 1- угол между касательными к кривым γ1 и
γ2 в точке z0.
Ф2 Ф1
- угол между касательными к кривым Г1 и
Г2 в точке w0.
8.
Угол между двумя кривыми, пересекающимисяв точке, в которой производная
отображающей функции отлична от нуля,
сохраняется по величине и направлению.
9.
Если совместить плоскости z и w так, чтобысовпали точки z0 и w0, а ось х совпала с осью u,
то, чтобы касательная к кривой γ1 совпала с
касательной к Г1, эту конфигурацию надо
повернуть на угол Argf ( z0 )
10.
Выясним геометрический смысл модуляпроизводной.
z - расстояние от точки z0 до точки
Δz+z0.
- расстояние от точки w0 до точки
Δw+w0.
Следовательно, величина
z
указывает, в каком отношении в результате
отображения
меняется
величина
расстояния между точками.
11.
Величинаf ( z0 )
являющаяся пределом отношения
z
z 0
при
называется коэффициентом растяжения
в точке z0.
Если f ( z0 ) 1
то в окрестности точки z0 расстояние
между точками увеличивается, и
наоборот.
12.
В силу аналитичности функции f(z) величинаf ( z0 )
не зависит от закона стремления z0 z z0
поэтому коэффициент растяжения в данной
точке постоянен.
13.
Отображение, обладающее свойствомпостоянства углов и свойством
постоянства коэффициента растяжения
в каждой точке, называется конформным
отображением 1 рода.
14.
Отображение, осуществляемоеаналитической функцией, является
конформным во всех точках, в которых
производная этой функции отлична от нуля.
Верно и обратное утверждение:
Если отображение, осуществляемое
функцией, конформно в
некоторой области, то эта функция
является аналитической в данной области.
15.
Отображение, отличающееся отконформного тем, что углы сохраняются
только по абсолютной величине,
но меняют направление
отсчета на противоположное, называется
конформным отображением 2 рода.














 mathematics
mathematics








