Similar presentations:
Благоприятствующие элементарные события. Вероятности событий. Опыты с равновозможными элементарными событиями. Случайный выбор
1.
Благоприятствующиеэлементарные события.
Вероятности событий. Опыты с
равновозможными
элементарными событиями.
Случайный выбор
9
Вероятность
и статистика
2.
Цель урокаУметь определять
благоприятствующие элементарные
события случайного опыта
Знать правило вычисления
вероятности события, используя
вероятности элементарных событий
Уметь вычислять вероятность
события в случайном опыте с
ра в н ов озмо жн ыми элементарными
событиями
Знать, что такое случайный выбор
9
Вероятность и статистика
Научиться находить
вероятность события в
случайном опыте с
равновозможными
элементарными
событиями
Задачи
3.
План урокаБлагоприятствующие
элементарные события
9
Вероятности событий
Вероятность и статистика
Опыты с равновозможными
элементарными событиями
Случайный выбор
Р е ш е н и е заданий
4.
ВопросыКак вы думаете?
Игральный кубик бросают два раза.
Сколько элементарных событий в опыте?
Чему равна вероятность каждого из них?
Дано множество чисел А = {1; 2; 3; 4; 5; 6}.
Как читается запись 5 ∈ А, 10 ∉ А?
9
Вероятность и статистика
В опыте два элементарных события.
Вероятность одного из них равна 0,75.
Чему равна вероятность второго
элементарного события?
5.
Случайные событияСлучайные события, п р о исходящие в рамках случайного опыта,
состоят из одного и л и нескольких элементарных событий
B = {a, d, e}, C = {b, c, d, e}
Вероятность и статистика
Любое случайное событие эксперимента с элементарными
событиями a, b, c, d, e, м о ж н о записать как множество с
п ер еч и слен и ем его элементов, например, А = {a, b, с},
9
6.
Благоприятствующие элементарные событияСлучайное событие А = {a, b, с}
состоит из трёх элементарных
событий а, b, c.
Говорят, что элементарные
события а, b, c
благоприятствуют событию А
9
Вероятность и статистика
Элементарные события,
благоприятствующие
событию А – это
элементарные события,
п р и которых событие А
наступает
7.
Случайное событие 9Вероятность и статистика
это множество, состоящее из
благоприятствующих ему
элементарных событий
8.
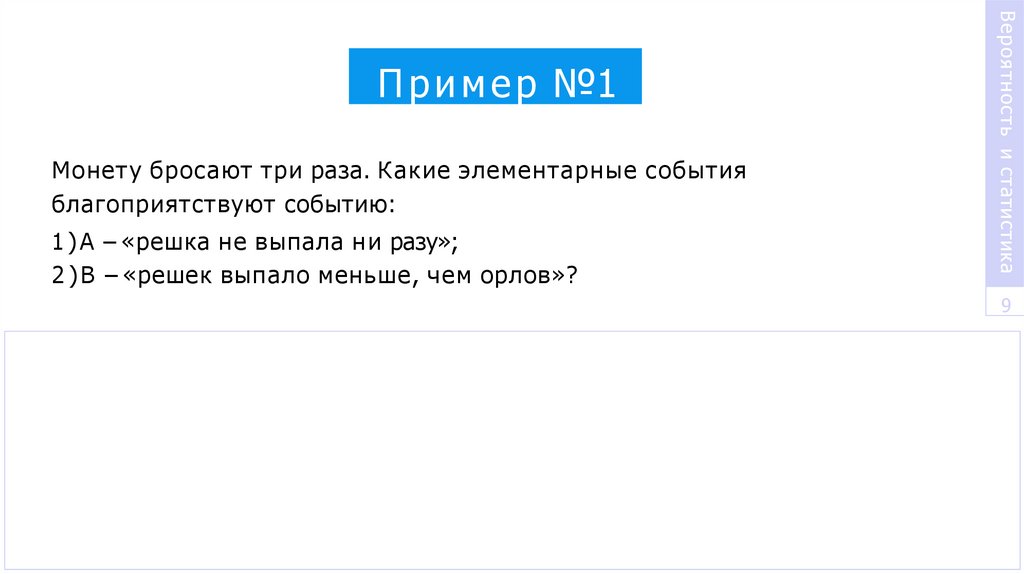
Монету бросают три раза. Какие элементарные событияблагоприятствуют событию:
1 ) А – «решка не выпала н и разу»;
2 ) В – «решек выпало меньше, чем орлов»?
Вероятность и статистика
П р и м е р №1
9
9.
РешениеВ опыте 23 = 8 элементарных событий. П е р е ч и с л и м их: РРР, РРО, РОР, РОО,
ООО, ОРО, ООР, ОРР.
1.Случайному событию А благоприятствует одно элементарное событие.
М о ж н о записать: А = {ООО}.
1. Четыре элементарных события являются благоприятствующими для
случайного события В. В = {РОО, ООО, ОРО, ООР}.
Ответ: 1. А = {ООО}; 2. В = {РОО, ООО, ОРО, ООР}
10.
Вероятность случайного событияПравило
Пусть событие А = {а, b, с, d},
тогда вероятность события А
равна:
Р(А) = Р(а) + Р(b) + Р(с) +P(d),
0≤ Р(А) ≤ 1
9
Вероятность и статистика
Вероятность случайного
события равна су мме
вероятностей
элементарных событий,
благоприятствующих
этому событию
11.
В случайном опыте пять элементарных событий: a, b, c, d, e. Известнывероятности этих событий: Р(а) = 0,05, Р(b)= 0,25, Р(с) = 0,3, Р(d) = 0,3,
P(e) =0,1. Найдите вероятности событий:
1 ) А = {a, b, с};
2 ) B = {a, d, e}
Вероятность и статистика
П р и м е р №2
9
12.
РешениеБудем использовать правило: вероятность случайного события равна
с у м м е вероятностей элементарных событий, благоприятствующих этому
событию.
1)Р(А) = Р(а) + Р(b) + Р(с) = 0,05 + 0, 25 +0,3 = 0,6;
2) Р(В) = Р(а) + Р(d) + P(e) =0,05 + 0,3 + 0,1 = 0,45.
Ответ: 1) 0,6; 2) 0,45
13.
Опыты с равновозмож н ым и элементарными событиямиПр ав и ло вычисления вероятности события
9
Вероятность и статистика
В случайном опыте с конечным числом равновозможных
элементарных событий вероятность случайного события равна
о тн о шению числа элементарных событий, благоприятствующих
этому событию, к о бщему числу элементарных событий
14.
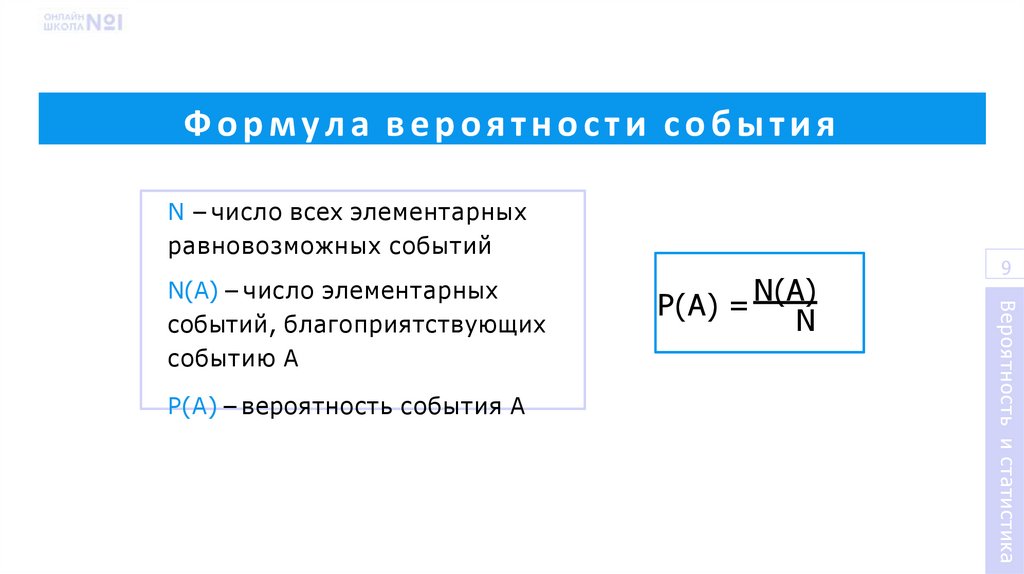
Формула вероятности событияN – число всех элементарных
равновозможных событий
Р(А) – вероятность события А
N(A)
Р(А) =
N
Вероятность и статистика
N(A) – число элементарных
событий, благоприятствующих
событию А
9
15.
Вероятность и статистикаП р и м е р №3
9
Игральную кость бросили два
раза. Найдите вероятность
события А –
«сумма выпавших очков
больше, чем 7»
16.
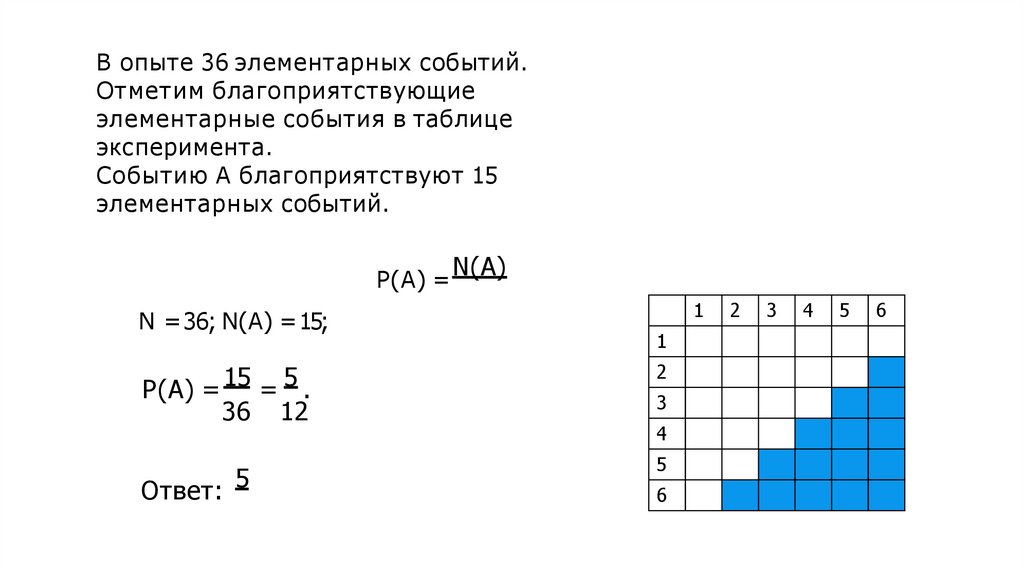
В опыте 36 элементарных событий.Отметим благоприятствующие
элементарные события в таблице
эксперимента.
Событию А благоприятствуют 15
элементарных событий.
Р(А) =
N = 36; N(A) =15;
N(A)
1
1
Р(А) = 15 = 5 .
36 12
2
Ответ: 5
5
3
4
6
2
3
4
5
6
17.
Случайный выборИзучаемая группа, из которой выбирают объекты для проведения
испытания, называется с о в о к у п н о с т ь ю и л и г е н е р а л ь н о й
с о в о к у п н о с т ь ю . Множество выбранных объектов называют
случайной выборкой из совокупности.
Вероятность собрать ту и л и иную выборку не зависит от способа
выбора. Последовательный выбор из всей совокупности предметов
м ож н о заменить одноврем е нн ым
9
Вероятность и статистика
С л у ч а й н ы й в ы б о р – ви д случайного опыта с равновозможными
элемен тар ным и событиями, когда из изучаемой группы
предметов делают выбор одного и л и нескольких предметов без
каких-либо предпочтений
18.
Из лотерейного барабана, в которомнаходятся шары с номерами от 1 до 100,
вынимают один шар. Какова вероятность того,
что номер вынутого шара не имеет цифры 6?
Вероятность и статистика
П р и м е р №4
9
19.
РешениеВ опыте 100 равновозможных элементарных событий, N = 100.
Подсчитаем количество благоприятствующих элементарных событий.
Содержат цифру 6 номера: 6, 16, 26, 36, 46, 56, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69,
76, 86, 96, всего 19 номеров. Значит, N(A) = 100 – 19 = 81.
Р(А) = N(A), Р(А) = 81 = 0,81.
N
100
Ответ: 0,81
20.
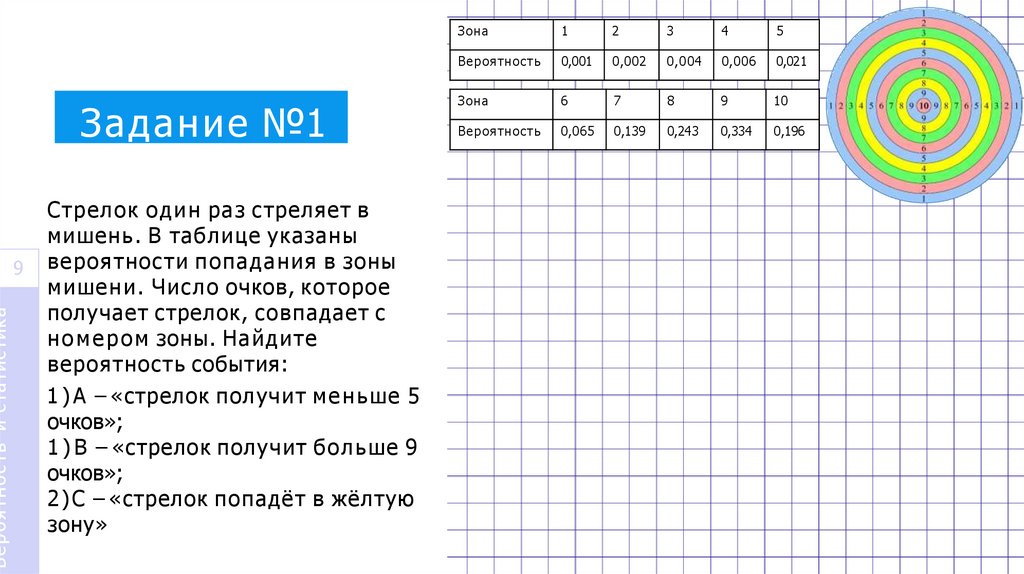
Вероятность и статистикаЗадание №1
9
Стрелок о д и н раз стреляет в
мишень. В таблице указаны
вероятности попадания в зоны
мишени. Число очков, которое
получает стрелок, совпадает с
н о м е р о м зоны. Найдите
вероятность события:
1 ) А – «стрелок получит м е н ь ш е 5
очков»;
1 ) В – «стрелок получит больше 9
очков»;
2 ) С – «стрелок попадёт в жёлтую
зону»
Зона
1
2
3
4
5
Вероятность
0,001
0,002
0,004
0,006
0,021
Зона
6
7
8
9
10
Вероятность
0,065
0,139
0,243
0,334
0,196
21.
В коробке лежат шары: 15 синих,8 красных и 2 белых. Из коробки
наудачу достают один шар.
Какова вероятность события:
1. A

























 mathematics
mathematics








