Similar presentations:
Решение задач линейного программирования в MS Excel
1. Решение задач линейного программирования в MS Excel
Подопригора Игнат Валерьевич, к.э.н.,доцент кафедры Экономики
2. Ответы задачи
1. Шкафов А - 300; Шкафов В - 2002. Курьерских поездов - 5; Скоростных - 7
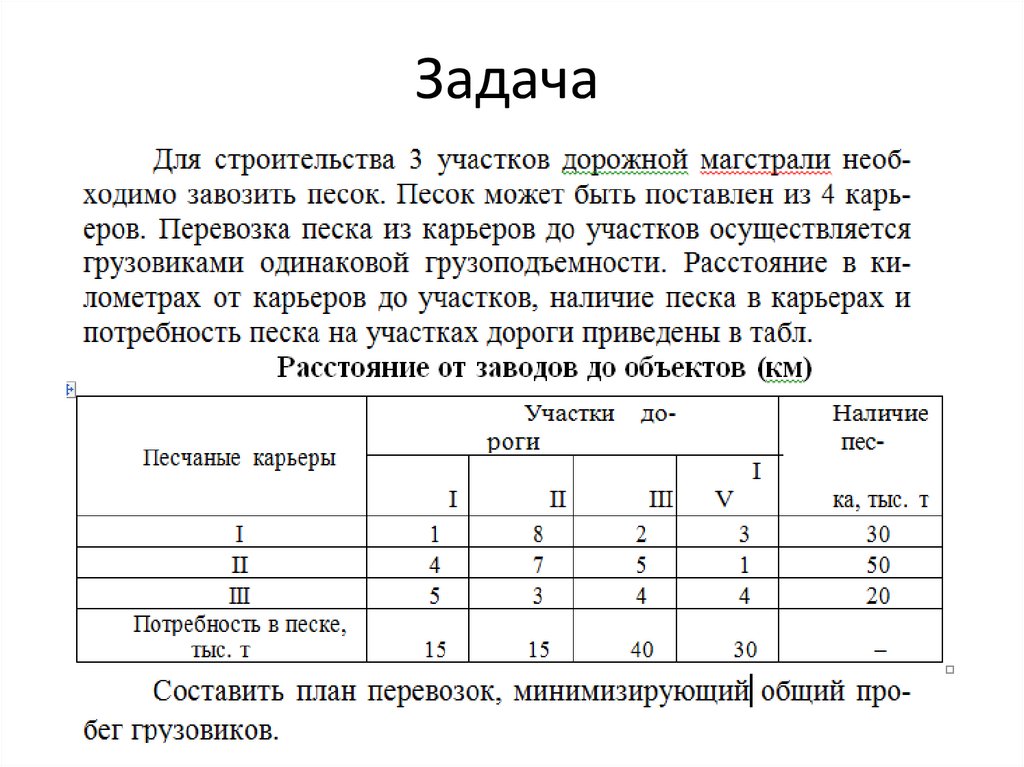
3. Задача 1
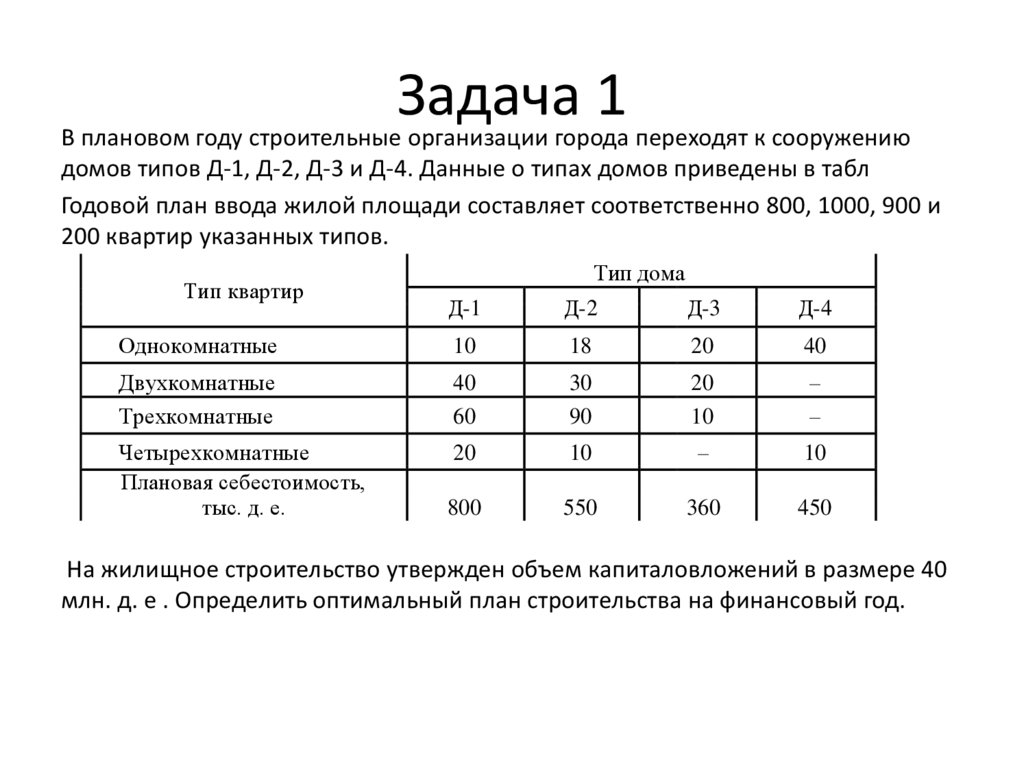
В плановом году строительные организации города переходят к сооружениюдомов типов Д-1, Д-2, Д-3 и Д-4. Данные о типах домов приведены в табл
Годовой план ввода жилой площади составляет соответственно 800, 1000, 900 и
200 квартир указанных типов.
Тип квартир
Тип дома
Д-1
Д-2
Д-3
Д-4
Однокомнатные
10
18
20
40
Двухкомнатные
Трехкомнатные
40
60
30
90
20
10
–
–
Четырехкомнатные
Плановая себестоимость,
тыс. д. е.
20
10
–
10
800
550
360
450
На жилищное строительство утвержден объем капиталовложений в размере 40
млн. д. е . Определить оптимальный план строительства на финансовый год.
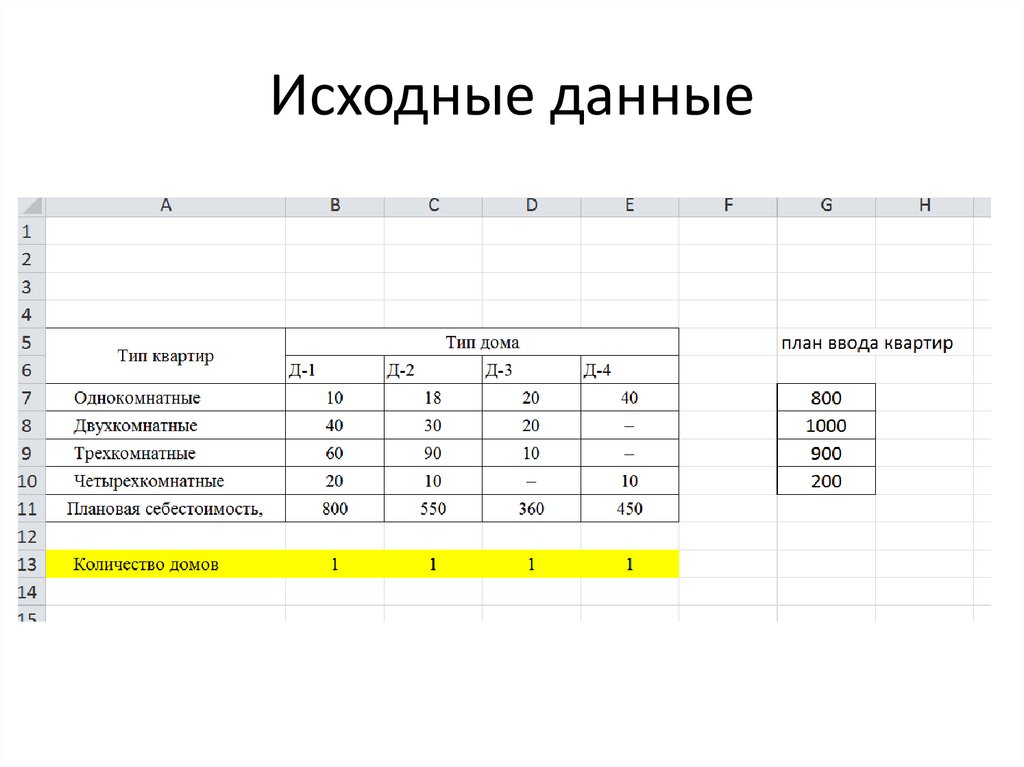
4. Исходные данные
5. Считаем количество квартир
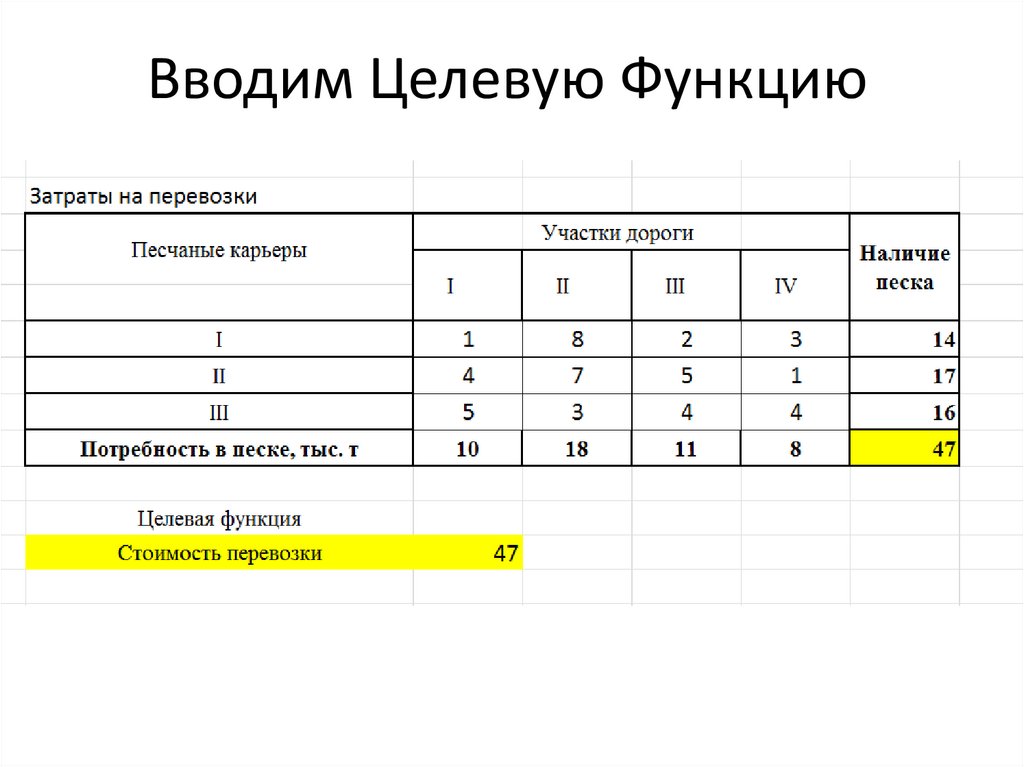
6. Вводим целевую функцию (себестоимость)
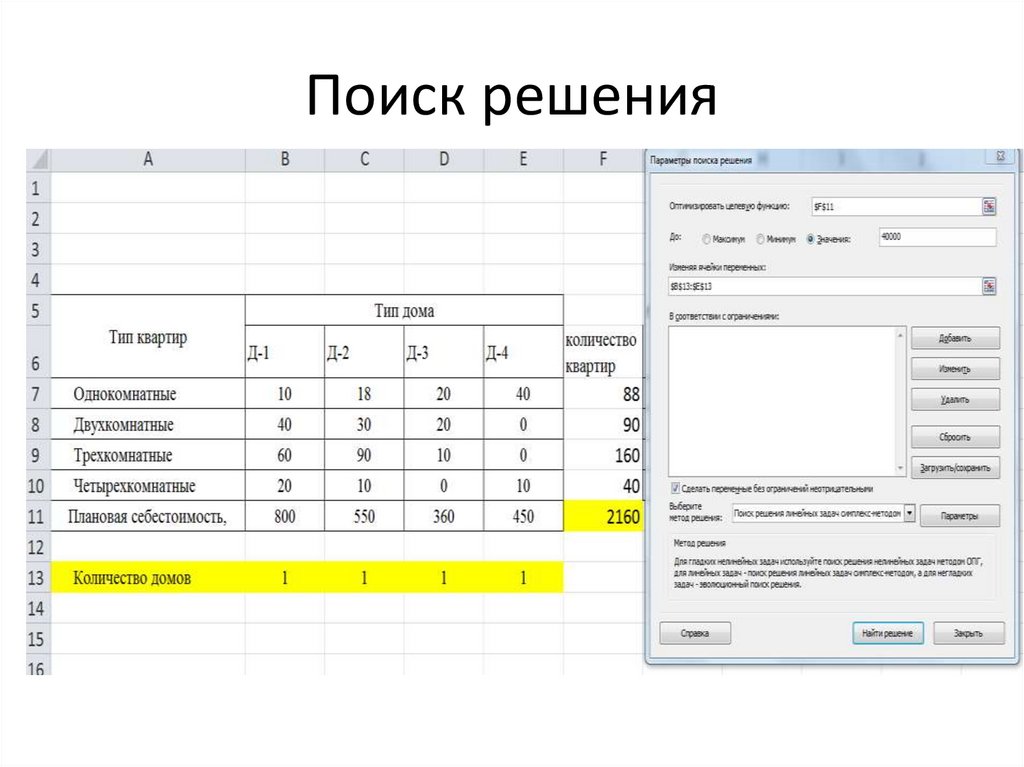
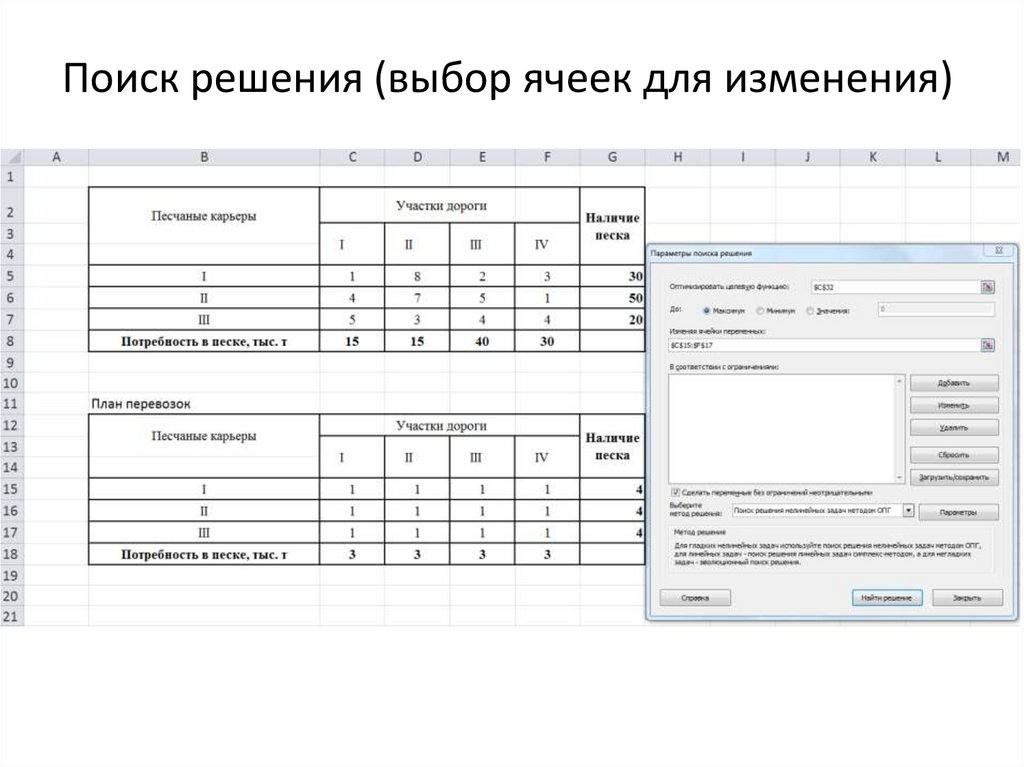
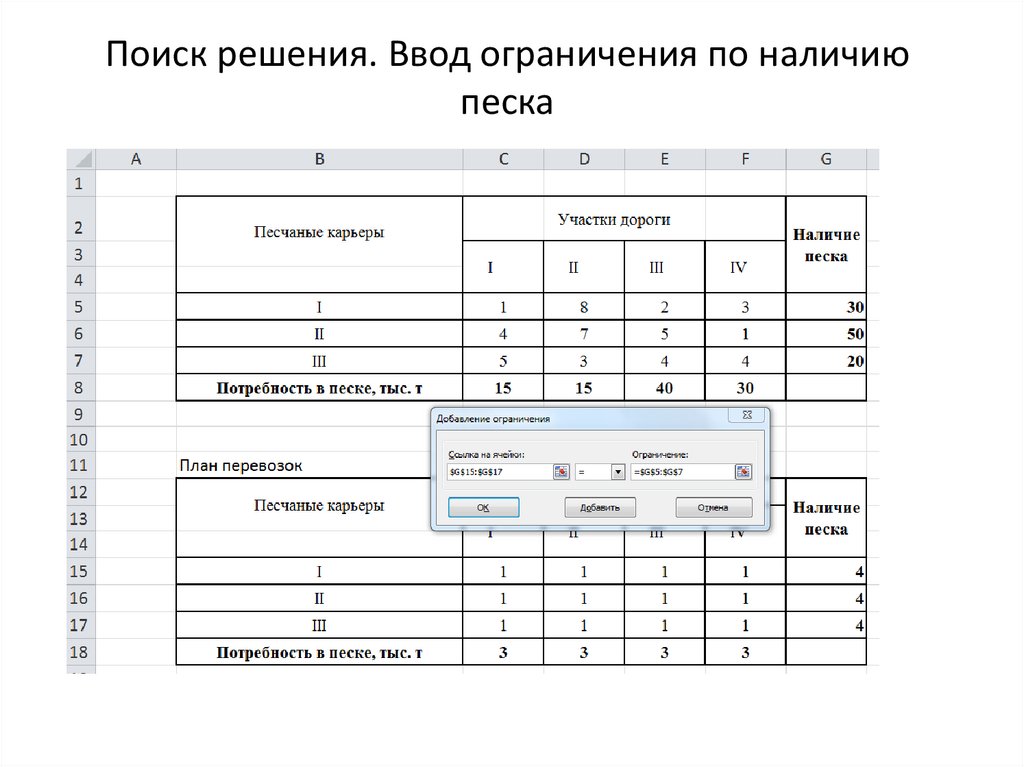
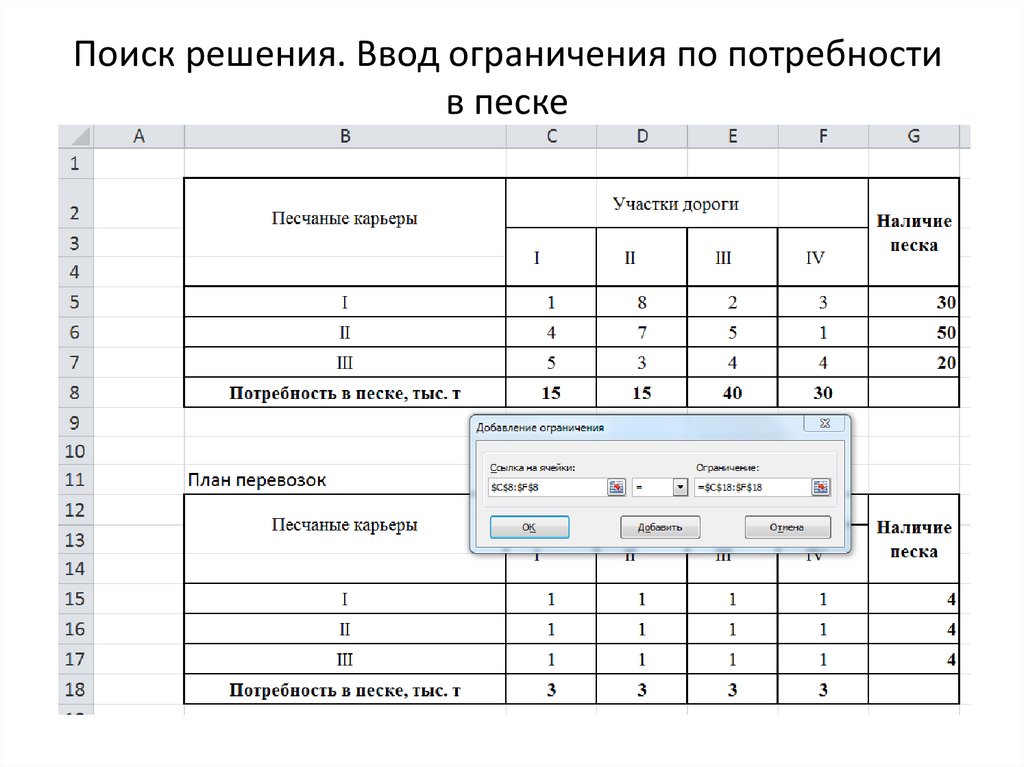
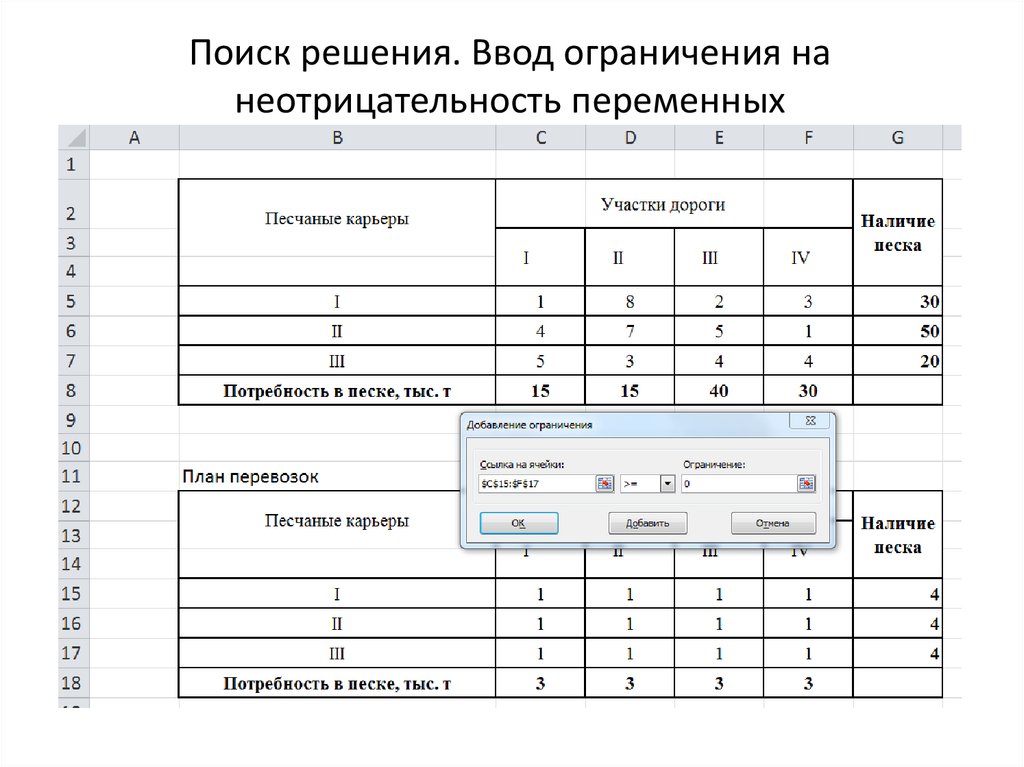
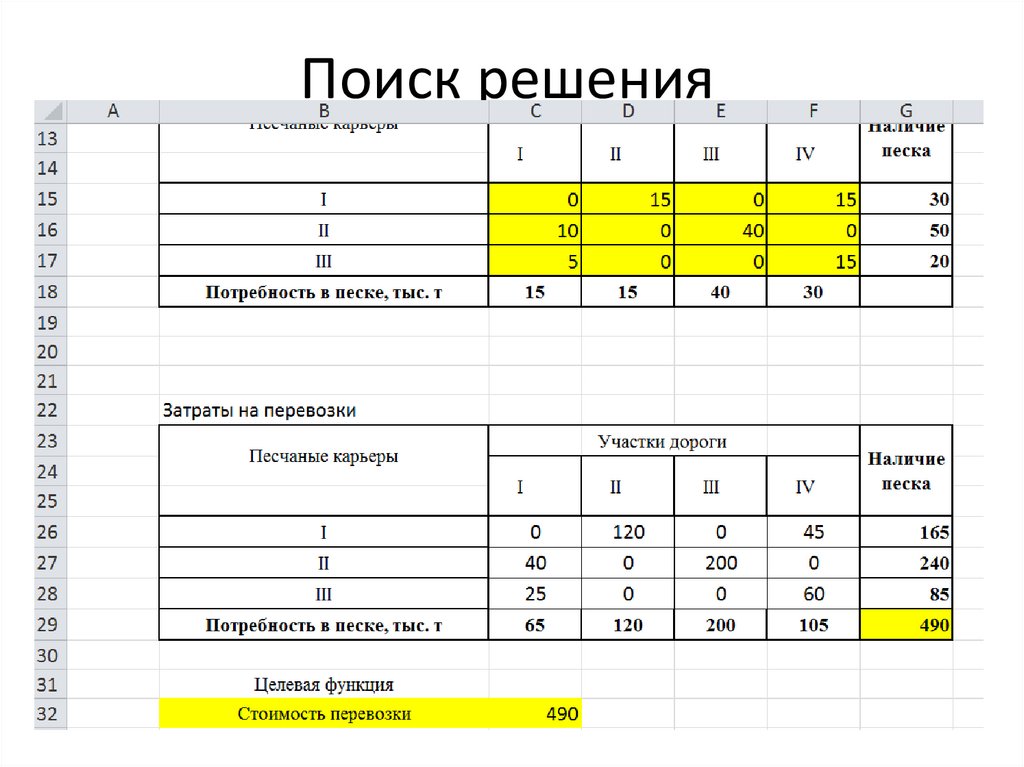
7. Поиск решения
8. Поиск решения
9. Поиск решения
10. Транспортная задача
Транспортная модель используется приразработке плана перевозок одного вида
продукции из нескольких пунктов отправления в
пункты назначения. При построении модели
используются:
величины, характеризующие предложение в
каждом исходном пункте и спрос в каждом пункте
назначения;
стоимость перевозки единицы продукции из
каждого исходного пункта в каждый пункт
назначения.
11.
Пусть однородный продукт, сосредоточенный в mотправления в количествах
a1 , a2 ,..., am
единиц, необходимо доставить в каждый из n
пунктов назначения в количествах
b1 , b2 ,..., bn
единиц. Стоимость перевозки единицы продукта
из i -го пункта отправления в j -й пункт
назначения равна
комбинаций i, j .
cij
и известна для всех
12.
Пустьxij– количество продукта,
перевозимого по маршруту i, j . Задача
заключается в определении таких величин
для всех маршрутов
xij , при которых
суммарная стоимость перевозок i, j
минимальна.
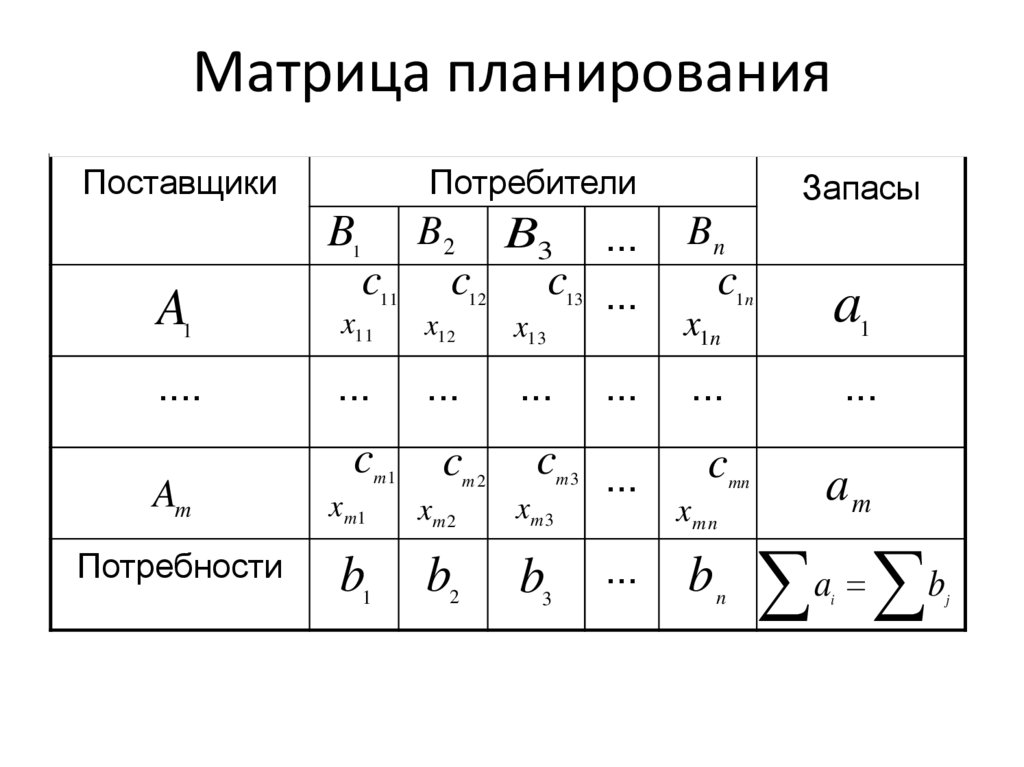
13. Матрица планирования
ПоставщикиПотребители
B
B2
1
c
B3 ...
c
c ...
A
x11
x12
x13
....
...
...
...
1
11
c
m1
12
c
m3
Am
x m1
xm 2
xm 3
Потребности
b
b
b
1
2
Bn
c
13
c
m2
Запасы
3
1n
x1n
...
...
...
c
...
xm n
b
n
a
1
...
mn
am
a b
i
j
14.
• Математическая модель транспортной задачисводится к минимизации целевой функции,
выражающей суммарные затраты на перевозку
всего груза
m n
Z cij xij min
i 1 j 1
15.
Систему ограничений получаем из следующихусловий задачи:
n
1. Все грузы должны быть вывезены, т.е.
xij 0;
n
j 1
xij ai , i 1,...,m .
m
j 1
n
x b
2. Все потребности должны быть удовлетворены,
i 1 j 1
ij
j
т.е.
m
xij b j , j 1,..., n .
i 1
16.
Тогда математическая модель транспортной задачиимеет следующее.найти наименьшее значение
линейной функции при ограничениях:
m
n
Z cij xij
i 1 j 1
n
xij ai
j 1
m
xij b j
i 1
x
0
.
ij
i 1, m
j 1, n
17.
• Это есть задача ЛП с m n уравнениями иmn неизвестными.
В рассмотренной модели предполагается, что
суммарные запасы равны суммарным потребностям
m
n
i 1
j 1
ai b j .
Такая модель называется закрытой
18.
• Теорема. Любая транспортная задача, у которой,n
m
ai b j
i 1
имеет решение.
j 1






















 mathematics
mathematics software
software








