Similar presentations:
Транспортная задача
1.
Выполнила:студентка 5 курса,
факультета Математики,
Информатики, Физики
Группы И - 51
Ченцова Е.А.
Научный руководитель:
Астахова Н.А. к. п. н. , доцент
2. Формулировка транспортной задачи
Транспортная задача в общем виде состоит вопределении оптимального плана перевозок
некоторого однородного груза
из m пунктов отправления А1 А2,,..., Аm
в n пунктов назначения B1 ,B2 ,…, Bn
В качестве критерия оптимальности можно взять
минимальную стоимость перевозок всего груза, либо
минимальное время его доставки.
3.
Неизвестными транспортной задачи являютсяобъёмы перевозок от каждого i-го поставщика
каждому j–му потребителю.
В транспортных задачах под поставщиками и
потребителями понимаются различные
промышленные и сельскохозяйственные предприятия,
заводы, фабрики, склады, магазины и т.д. Под
стоимостью перевозок понимают тарифы, расстояния,
время, расход топлива и т.п.
4.
Рассмотрим задачу с первым критерием(минимальная стоимость перевозок всего груза),
обозначив:
Cij - тарифы перевозок единицы груза из i-гo
пункта отправления в j-й пункт назначения
ai - запасы груза в пункте Аi
bj - потребности в грузе пункта Bj
xij - количество единиц груза, перевозимого из i-гo
пункта в j-й пункт.
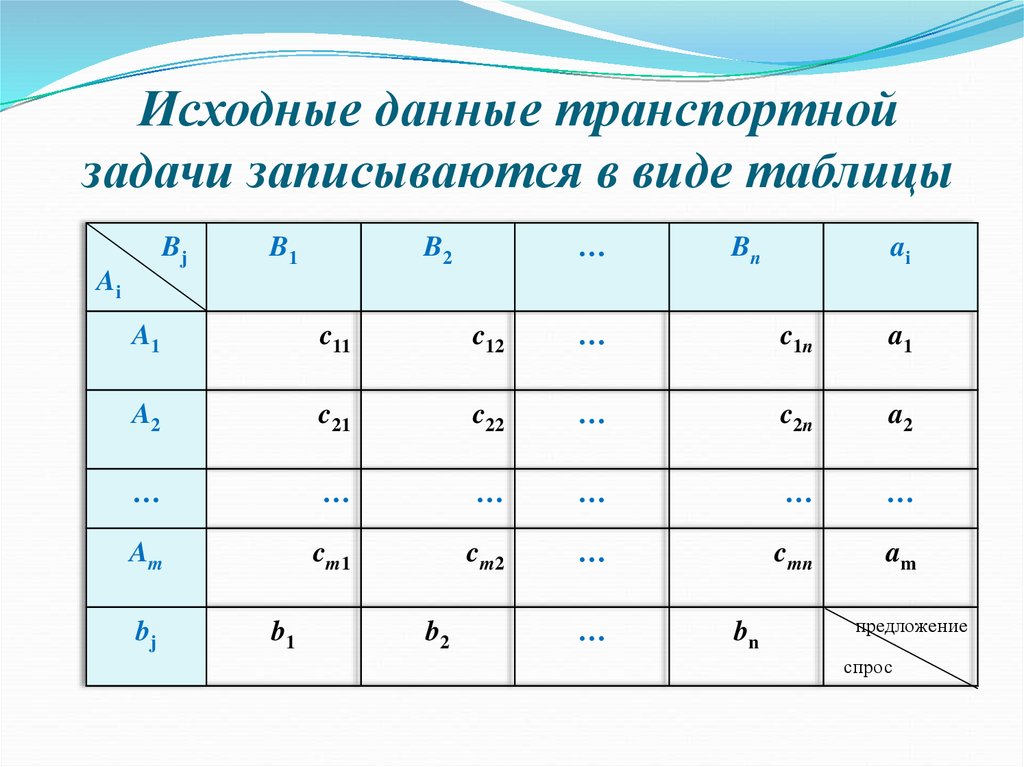
5. Исходные данные транспортной задачи записываются в виде таблицы
BjB1
…
B2
Bn
ai
Ai
A1
c11
c12
…
c1n
a1
A2
c21
c22
…
c2n
a2
…
…
…
…
…
…
Am
cm1
cm2
…
cmn
am
bj
b1
b2
…
bn
предложение
спрос
6.
Целевая функция имеет вид:m
n
Z cij xij
i 1 j 1
7. Система ограничений состоит из двух групп уравнений
Первая группа из m уравнений описывает тот факт,что запасы всех поставщиков вывозятся полностью:
n
x
j 1
ij
ai
i = 1, 2, …, m.
8.
Вторая группа из n уравнений выражает требованиеполностью
удовлетворить
запросы
всех
n
потребителей:
m
xij b j ,
j = 1, 2,…, n
i 1
Кроме этого, переменные задачи должны быть
неотрицательны:
xij 0
i = 1, 2, …, m
j = 1, 2, …, n
9. Формулировка транспортной задачи такова:
Найти переменные задачи X ( xij ), i 1,2,...n, j 1,2,...m,удовлетворяющие системе ограничений ,
n
xij ai
j 1
m
i = 1, 2, …, m
xij b j
j = 1, 2, …, n
i 1
а также условию неотрицательности переменных
и обеспечивающие минимум целевой функции
Z
m
n
c
i 1
j 1
ij
xij
10.
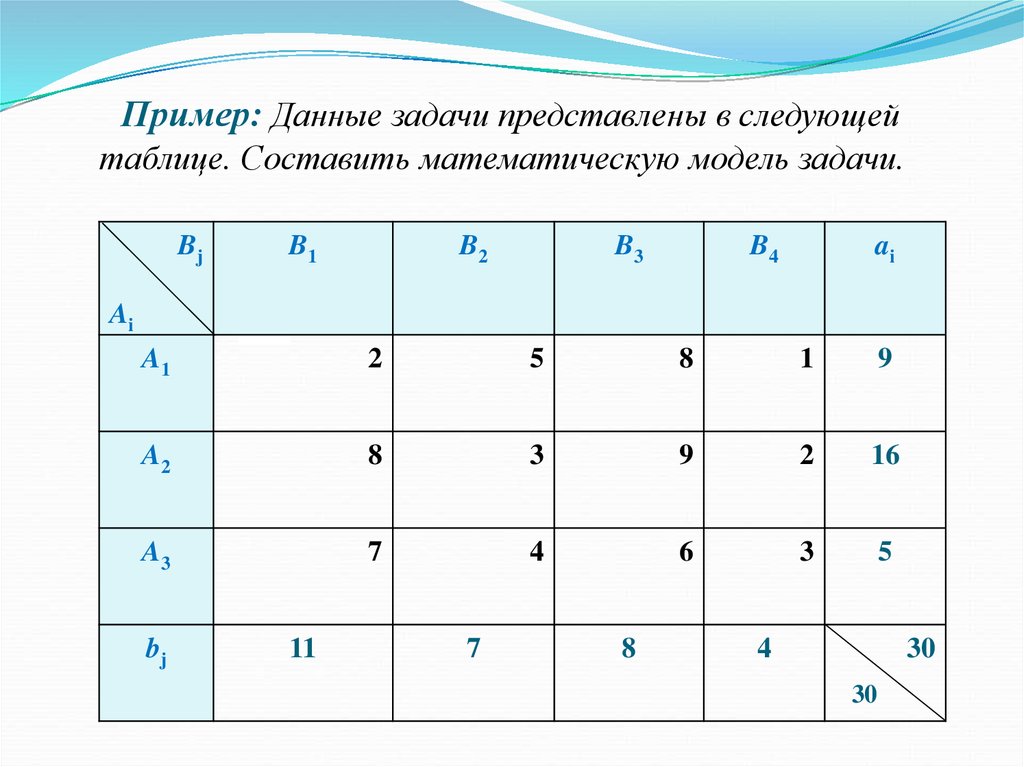
Пример: Данные задачи представлены в следующейтаблице. Составить математическую модель задачи.
Bj
B1
B2
B3
B4
ai
Ai
A1
2
5
8
1
9
A2
8
3
9
2
16
A3
7
4
6
3
5
bj
11
7
8
4
30
30
11.
Решение: Пусть xij - объемы перевозок груза от i-гопоставщика – j-му потребителю. В таблице
представлены затраты на перевозку единицы груза от
поставщика – потребителю.
Целевая функция имеет вид :
Z 2 x11 5 x12 8 x13 x14 8 x21 3 x22 9 x23
2 x24 7 x31 4 x32 6 x33 3 x34 min
12. при ограничениях
1)x11 x12 x13 x14 9
x 21 x 22 x 23 x 24 16
x31 x32 x33 x34 5
n
(Условие
x11
2)
xij
a i , i = 1, 2, …, m)
j 1
x 21 x31 11
x12 x 22 x32 7
x13 x 23 x33 8
x14 x 24 x34 4
m
(Условие
x ij
i 1
j = 1, 2, …, n)
bj
13. Опорный и оптимальный план транспортной задачи
Всякое неотрицательное решение систем ограниченийопределяемое матрицей X = (xij ), называют опорным
планом ТЗ, а план при котором функция Z принимает
минимальное значение - называется оптимальным
планом ТЗ.
14. Необходимое и достаточное условие разрешимости транспортной задачи
Если общее количество груза в пунктах отправления иобщая потребность в нем в пунктах назначения
совпадают, т.е.
m
a
i 1
i
n
b
j 1
j
Модель такой задачи называется закрытой,
в противном случае открытой.
15. Искусственные потребители и поставщики
Если спрос меньше предложения, то необходимовводить искусственного потребителя Bn+1
Если спрос больше предложения, то необходимо
вводить искусственного поставщика Am+1
16. Используемая литература:
Борзунова Т.Л., Барыкин М.П. , Данилов Е.А.Соловьева О.Ю. - Математическое моделирование:
учебное пособие/ВолгГТУ, - Волгоград, 2008.
Конюховский П.В. Математические методы
исследования операций в экономике – СПб: Питер,
2000.














 mathematics
mathematics economics
economics