Similar presentations:
Транспортная задача
1.
Транспортная задача2. Транспортная задача
Отдельные задачиоптимальной
загрузки
промышленного
оборудования
Оптимальное
распределение
объемов выпуска
промышленной
продукции между
заводамиизготовителями и др.
Взаимная привязка
грузопотоков
прямого и
обратного
направлений
Задачи,
относящиеся
к
транспортным
Привязка пунктов
отправления к
пунктам
назначения
Прикрепление
потребителей
ресурса к
производителям
3.
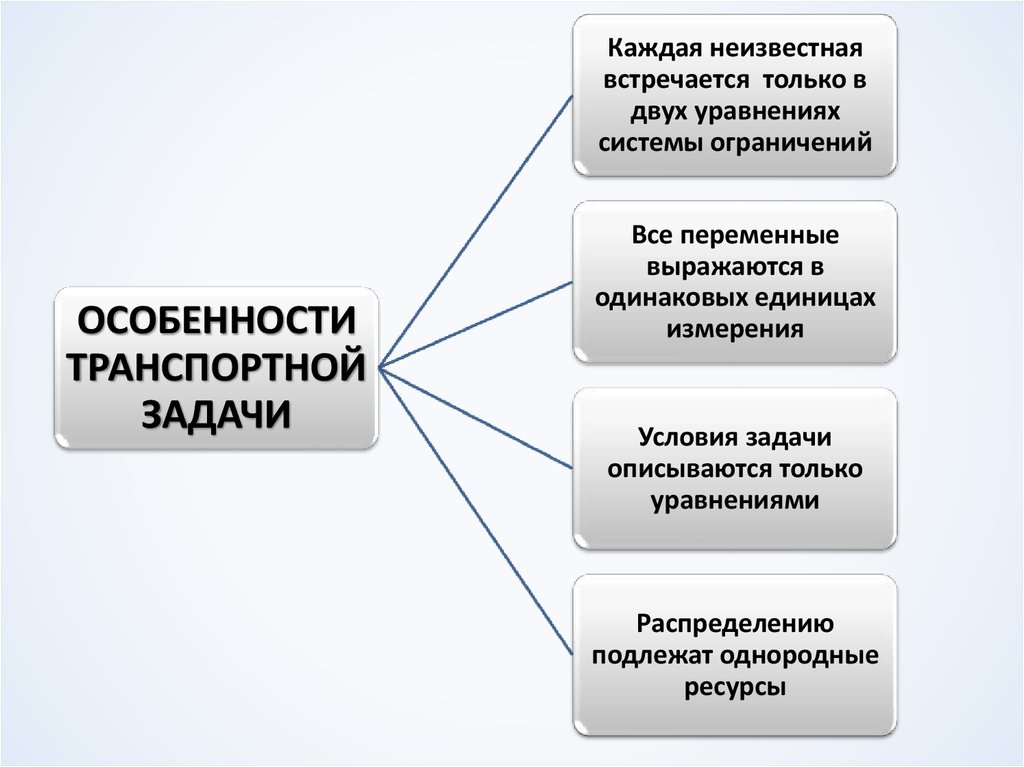
Каждая неизвестнаявстречается только в
двух уравнениях
системы ограничений
ОСОБЕННОСТИ
ТРАНСПОРТНОЙ
ЗАДАЧИ
Все переменные
выражаются в
одинаковых единицах
измерения
Условия задачи
описываются только
уравнениями
Распределению
подлежат однородные
ресурсы
4.
Число пунктов производства – mai , i 1,2,.., m –количество продукта, произведенного на i
пункте
Количество пунктов потребления – n
b j , j 1,2,.., n –потребность j пункта потребления
c ij - цена перевозки единицы продукта из i пункта производства
в j пункт.
Классическая постановка задачи
Требуется организовать перевозку продукции из пункта
производства в пункт потребления, так чтобы весь товар из
пунктов производства был вывезен, удовлетворить потребности
пунктов потребления и минимизировать стоимость перевозки.
5. Математическая модель транспортной задачи
x ij - количество единиц продукта, перевозимого с i пунктапроизводства в j пункт
количество продукта, вывезенного с i пункта производства
n
x
j 1
ij
ai , i 1,2,.., m
количество единиц продукта
m
x
i 1
ij
b j , j 1,2,.., n
Критерий – суммарные затраты
m
n
i 1
j 1
f cij xij min
6.
7. Свойства транспортной задачи
Утверждение 1. Транспортная задача разрешима тогда итолько тогда, когда выполнено условие баланса:
m
n
a b
i 1
i
j 1
j
Такая транспортная задача называется закрытой.
Утверждение 2. Ранг матрицы ограничений транспортной
задачи равен m+n-1
8. Приведение открытой транспортной задачи к замкнутой
Пусть выполнено:Вводиться фиктивный пункт потребления:
,
9. Начальная таблица транспортной задачи. Метод северо-западного угла.
1. Выбрали клетку c координатами (i,j) –свободная северо-западная.2. ai b j , то xij ai . Ставим прочерки во всех свободных клетках i
строки
ai b j , то xij b j . Ставим прочерки во всех свободных клетках j
столбца
ai b j , то xij b j . Ставим прочерки во всех свободных клетках j
столбца либо i строки
3. Пересчитываем
ai : ai - xij
b j : b j - xij
4. До тех пор пока везде не будут числа или прочерками.
Клетки в которых числа - базисные. Клетки с прочерками не
базисные. Количество базисных клеток=m+n-1.
10.
Метод минимального элемента.В методе северо-западного угла выбираем не самую северо-западную
клетку, а клетку с минимальной стоимостью перевозки.
Метод потенциалов.
Шаг1. Проверка на оптимальность
Шаг 2. Если опорное решение не оптимально, то шаг 1.
Проверка на оптимальность.
В каждой базисной клетке (i,j): ui
Уравнение данного вида: m+n-1
Число переменных: m+n
Положим
u1 0
В каждой не базисной клетке
Если все
v j cij
ij ui v j cij
ij 0 , то опорное решение оптимальное.
Иначе, сществует по крайней мере одна (k,l)
kl 0
11.
Определение. Циклом назовем последовательный набор клеток, вкотором любые две клетки находятся в одной строке или столбце
таблицы. И никакие три соседние клетки не находятся в одной
стоке или столбце. Первая и последняя клетка цикла должна
быть из одной строки или столбца.
Множество клеток с меткой «- » обозначим
Константа пересчета:
K
min xij
i , j K
Пересчет клеток цикла:
x
,
(
i
,
j
)
K
ij
xij :
x
,
(
i
,
j
)
K
ij
Любую клетку с нулем выводим из базиса. В новой таблице в этой
клетке ставим «–».
Если несколько нулей после пересчета, то выводим все равно
только одну клетку из базиса, остальные считаем базисными.
12. Экономические задачи, которые сводятся к транспортной задаче
Отдельные поставки от определенных поставщиков некоторымпотребителям должны быть исключены
На предприятии необходимо определит минимальные затраты на
производство и транспортировку продукции
Ряд транспортных маршрутов, по которым необходимо доставить грузы,
имеют ограничения по пропускной способности
Поставки по определенным маршрутам обязательны и должны войти в
оптимальный план независимо от того, выгодно это или нет
Распределение производства изделий между предприятиями
Необходимо максимизировать целевую функции задачи транспортного типа
Многопродуктовые транспортные задачи
13.
В матрице перевозок, содержащей оптимальный план,определенные клетки оставались свободными.
Способ перехода:
Искусственное завышением затрат на перевозки Сij в клетках,
перевозки через которые следует запретить.
14.
Критерий оптимальности – суммазатрат на производство и транспортировку
продукции.
15.
По маршруту AjBj можно провести не более q единицгруза.
Bj –B'j и В''j
b'j = bj - q,
b''j = q
В первом столбце B'j в клетке i ставится искусственно
завышенный тариф М (клетка блокируется).
16. Модели конфликтов
17. Принятие решений в конфликтных ситуациях
Математическая модель - игра.Игра — это совокупность правил, описывающих
конфликтной ситуации. Эти правила устанавливают:
сущность
выбор образа действия игроков на
каждом этапе игры;
информацию, которой обладает
каждый игрок при осуществлении
таких выборов;
плату для каждого игрока после
завершения любого этапа игры.
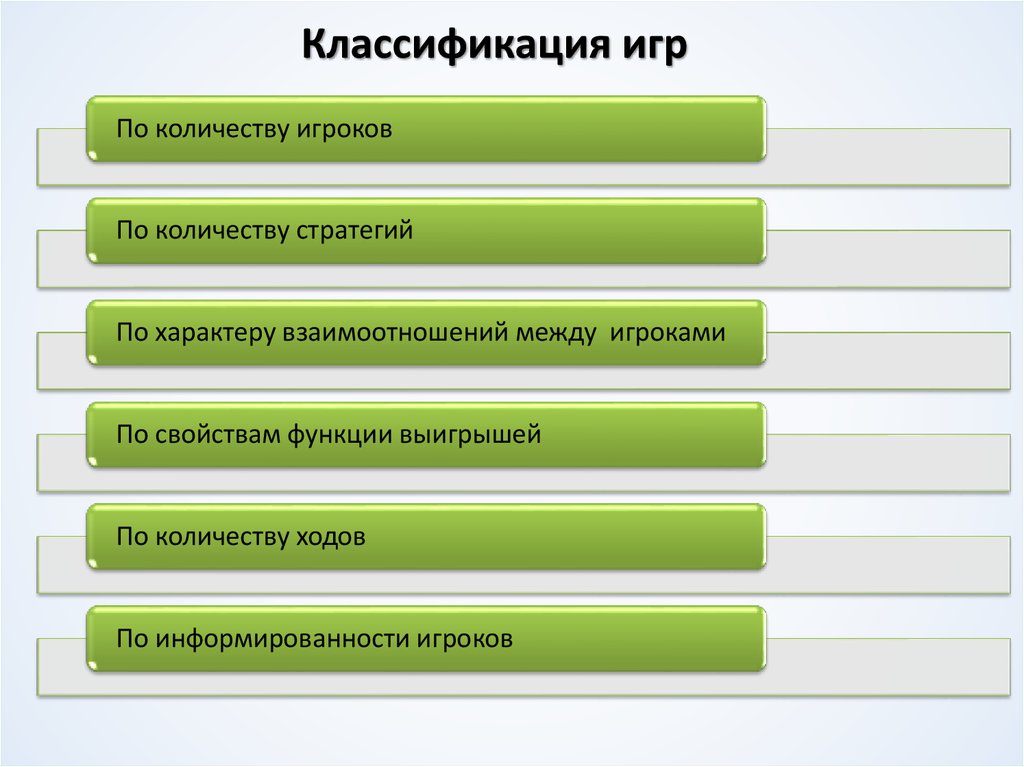
18. Классификация игр
По количеству игроковПо количеству стратегий
По характеру взаимоотношений между игроками
По свойствам функции выигрышей
По количеству ходов
По информированности игроков
19. Конфликты интересов
Антагонистические конфликты20.
Определение (матричной игры с нулевой суммой).S1 1,.., n1 .
S2 1,.., n2 .
An1 n2 aij
Матричной игрой с нулевой суммой наз. тройка объектов
S1, S2 , A .
Смешанная стратегия 1-го игрока – вектор вероятности выбора
стратегии p p1,.., pn1 .
n1
pi 1
P : i 1
,
pi 0
21.
Смешанная стратегия 2-го игрока – q q1,.., qn2 .n2
q j 1
Q : j 1
q j 0
Чистая стратегия:
e (0,..,0,1,0,..,0)
i
22.
n1n2
H p, q aij pi q j
i 1 j 1
Тройка
p* , q* , v
называется оптимальным решением
*
*
-цена
v
H
p
,
q
в смешанных стратегиях игры, где
игры, если:
H p, q* v H p* , q* H p* , q .(1)
*
*
i
,
j
, v - оптимальное решение в чистых стратегиях, если
Тройка
aij* ai* j* ai* j
Стратегия i0 1-го игрока наз. максиминной, если
min ai0 j max min aij v
j
i
j
23.
Стратегия j0 2-го игрока наз. минимаксной, еслиmax aij0 min max aij v
i
j
i
Лемма. Матричная игра разрешима в чистых стратегиях тогда и
только тогда, когда
v v.
Правило построения решения:
Если матрица А имеет седловую точку i0 , j0 .
В каждой стоке ищем минимальное значение и потом из всех
минимумов выбираем максимум- это v
В каждом столбце ищем максимум и из них выбираем минимумэто v
Если
v v , то получили решение
24.
Теорема фон Неймана-Нэша(основная теорема матричных игр)Любая матричная игра разрешима в смешанных стратегиях, при этом
max min H ( p, q) min max H ( p, q) v
p
q
q
p
p * , q * , v - оптимальное решение, где p * -смешанная максиминная
*
min
H
(
p
, q) max min H ( p, q)
стратегия
q
p
q
*
где q -смешанная минимаксная
*
max
H
(
p
,
q
) min max H ( p, q)
стратегия
p
q
p
25. Конфликты распределения
Кооперативные игры26. Основные понятия и определения
Определение. Кооперативной игрой в форме характеристическойфункции называется пара G ( N , v) ,
где N {1,2,.., n}
v -функция, ставящая
в
подмножеству множества
N вещественное число,
соответствие
каждому
непустому
v : 2N R
Определение. Непустое подмножество S множества
коалицией.
N называется
v S - максимальный выигрыш, который может получить коалиция
S независимо от поведения других игроков.
27.
Определение. Исходом игры называется векторx ( x1 , x2 ,.., xn ) ,
где xi - платеж i-му игроку
Если все игроки объединены в максимальную коалицию, то должно
выполнятся условие коллективной рациональности
x
i
v N
(1)
i N
Определение. Исход, удовлетворяющий (1) и условию (2)
xi v i , i N
(2)
называется дележом. Множество всех дележей обозначается D v
Условие (2) – индивидуальная рациональность.
28. С-ядро
Дележ х нестабилен из-за коалиции S N , еслиС-ядро кооперативной игры:
v S xi
i S
.
.
Утверждение.
С-ядро кооперативной игры является
выпуклым многогранником
29.
Цена Шепли:i v
S N
S 1 ! n S ! v S v S \ i
n!
Простая игра :
v S 0 или v S 1 для
всех
S N
Цена Шепли для простой игры:
i v
S N ,v S 1,v S \ i 0
S 1 ! n S !
n!



























 mathematics
mathematics