Similar presentations:
Оптимизация плана перевозок: транспортная задача. Тема 5
1. Оптимизация плана перевозок: транспортная задача
Тема 51
2. План лекции
2I Постановка задачи
II Метод потенциалов решения ТЗ
III Пример решения
3. Транспортная задача линейного программирования
Общая постановка транспортной задачи: состоит вопределении оптимального плана перевозок однородного
груза из m пунктов отправления
потребления
A1 ,…, A m
в n пунктов
B1 , B 2 ,…, B n .
Критерий оптимальности - минимальная стоимость
перевозок всего груза.
Мощности поставщиков и запросы потребителей, а
также затраты на перевозку единицы груза для каждой пары
«поставщик-потребитель» будем сводить в таблицу поставок.
3
4. Табличная форма записи исходных данных транспортной задачи
Пунктотправления
1
2
i
…
m
Потребность в грузах, bj
Пункт назначения
1
c11
x11
c21
x21
ci1
xi1
cm1
xm1
b1
2
c12
x12
c22
x22
ci2
xi2
cm2
xm2
b2
J…
c1j
x1j
c2j
x2j
cij
xij
cmj
xmj
bj
Запасы груза
ai
n
c1n
x1n
c2n
x2n
cin
xin
cmn
xmn
bn
a1
a2
ai
am
ai = bj
где
ai – запас груза у i-го поставщика, i=1..m;
bj – потребность в грузе у j-го потребителя, j=1..n;
cij – затраты на перевозку 1 ед. груза от i-го поставщика к j-му
потребителю, i=1..m j=1..n
хij – количество груза, перевозимого от i-го поставщика к j-му потребителю,
i=1..m j=1..n (искомые переменные)
4
5. Математическая модель транспортной задачи закрытого типа
Целевая функция:m n
f (X) C ij x ij min
i 1 j 1
Ограничения по строкам:
количество перевозимых грузов из i-го пункта отправления в j-е пункты назначения равно запасу i-го пункта
отправления.
n
x ij a i , (i 1...m) .
j 1
Ограничения по столбцам:
количество перевозимых грузов из i-х пунктов отправления в j-й пункт назначения должно равняться потребности
в j-м пункте назначения.
m
x ij b j j 1...n .
i 1
Условие неотрицательности переменных:
x ij 0 .
Балансовое условие: Количество всех распределяемых грузов и количество всех потребностей в грузах должны
быть равны:
m
n
i 1
j 1
a i b j .
5
6. Закрытая и открытая ТЗ
ЕслиЕсли
m
n
i 1
j 1
a i b j , то модель задачи закрытая; в противном случае открытая.
m
n
i 1
j 1
a i b j , то для решения открытую модель задачи приводят к закрытому виду
путем введения фиктивного пункта отправления с запасом, равным:
n
a m 1 b j
j 1
m
ai .
i 1
Стоимости перевозок грузов по фиктивному пункту полагают равными 0.
С m +1,j = 0, (j=1,2,...n).
Если
m
n
i 1
j 1
a i b j , то для решения модель задачи приводят к закрытому виду путем введения
фиктивного пункта назначения с потребностью, равной:
C i,n +1 = 0, (i=1,2,...m) .
6
7. Идея решения ТЗ
Теорема: ТЗ всегда имеет оптимальноерешение т.т.т. когда она закрытого типа
I Построение начального опорного любым
известным методом
II Улучшение начального плана методом
потенциалов
7
8. Метод потенциалов решения транспортной задачи
Величинаv j , j 1, n
– потенциал j-го потребителя, который при данном опорном плане
характеризует затраты на размещение одной единицы поставляемой продукции
указанному потребителю.
Величина
u i , i 1, m
– потенциал i-го поставщика, который при данном опорном плане
характеризует затраты на поставку одной единицы продукции от указанного поставщика.
Критерий оптимальности в методе потенциалов
ТЕОРЕМА. Если для некоторого опорного плана транспортной задачи будет
выполняться v j u i cij 0 для клеток с x ij 0 и v j u i cij 0 для клеток с x ij 0 , то этот
план является оптимальным.
8
9. Поиск начального опорного плана. Метод северо-западного угла
Поиск начального опорного плана. Метод северозападного углаВ верхнюю левую клетку (северо-западный угол) таблицы поставок записываем наименьшее из
чисел b1 и а1, пересчитываем запасы и потребности и столбец, с исчерпанным запасом, или строку с
удовлетворенной потребностью исключаем из дальнейшего расчета.
В оставшейся части таблицы снова находим северо-западный угол, заполняем эту клетку,
вычеркиваем строку или столбец и опять обращаемся к северо-западному углу и так далее.
Важнейшим условием построения опорного плана является назначение в выбранной клетке
наибольшего возможного плана перевозки.
9
10. Поиск начального опорного плана. Метод минимальных цен
В клетку с минимальным тарифом таблицы поставок записываем наименьшее из чисел bj и аi,пересчитываем запасы и потребности и столбец, с исчерпанным запасом, или строку с
удовлетворенной потребностью исключаем из дальнейшего расчета.
В оставшейся части таблицы снова находим клетку с наименьшим тарифом, заполняем эту клетку,
вычеркиваем строку или столбец и опять обращаемся к северо-западному углу и так далее.
Если есть несколько клеток с равным тарифом, построение плана можно начинать с любой из них.
10
11. Алгоритм решения транспортной задачи методом потенциалов
1. Находим первоначальный "невырожденный" опорный план одним из известных методов.2. Вычисляем потенциалы ui и vj решая систему для всех заполненных клеток: u i v j c ij x ij 0
3. Проверяем критерий оптимальности. Рассчитываем значения оценок для свободных клеток:
d ij u i v j c ij x ij 0 .
Если все оценки неположительные d ij 0 текущий опорный план оптимален, конец алгоритма. Иначе
переходим к следующему шагу.
4. Построение цикла пересчета.
а) в качестве клетки пересчета выбираем свободную клетку с максимальной положительной оценкой;
б) строим цикл пересчета – замкнутая ломанная линия, вершины которой лежат в заполненных
клетках, начало и конец в клетке пересчета, звенья вдоль строк и столбцов таблицы;
в) отмечаем клетку пересчета знаком (+) и строим цикл пересчета, последовательно присваивая
клеткам цикла знаки (–) и (+), начиная с клетки пересчета;
г) в клетках, помеченных знаком (–), находим наименьшую поставку и отнимаем ее от клеток (–), а к
клеткам (+) прибавляем. При этом клетка, содержащая наименьшую поставку, освобождается;
5. Возвращаемся к п. 2.
11
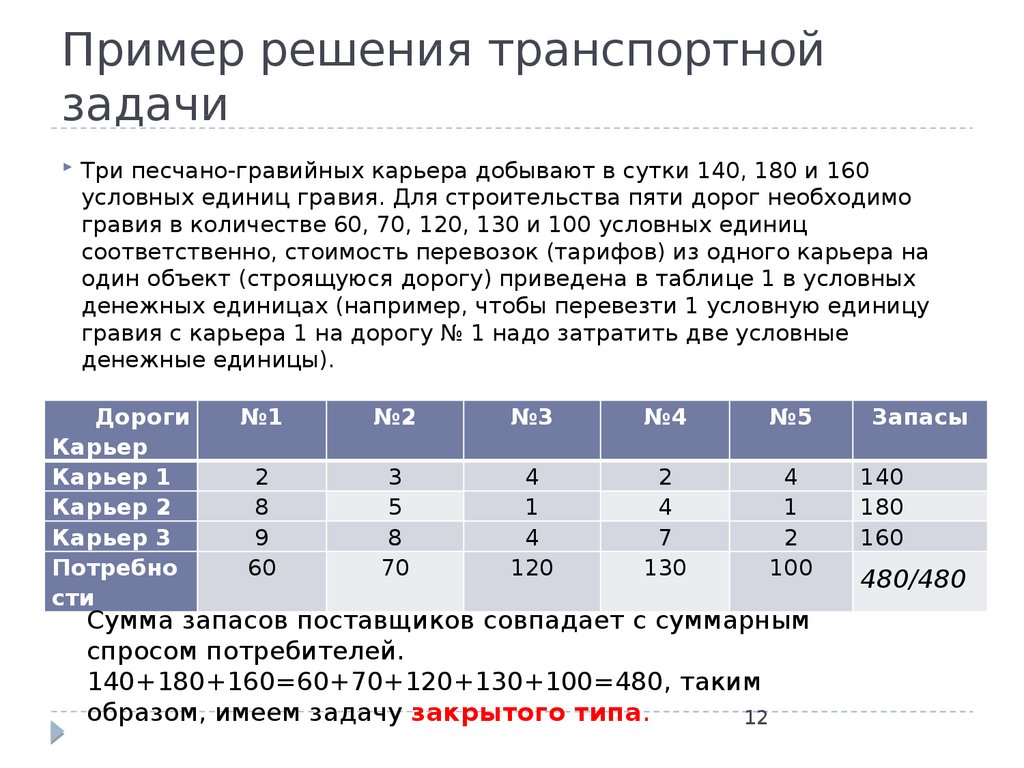
12. Пример решения транспортной задачи
Три песчано-гравийных карьера добывают в сутки 140, 180 и 160условных единиц гравия. Для строительства пяти дорог необходимо
гравия в количестве 60, 70, 120, 130 и 100 условных единиц
соответственно, стоимость перевозок (тарифов) из одного карьера на
один объект (строящуюся дорогу) приведена в таблице 1 в условных
денежных единицах (например, чтобы перевезти 1 условную единицу
гравия с карьера 1 на дорогу № 1 надо затратить две условные
денежные единицы).
Дороги
Карьер
Карьер 1
Карьер 2
Карьер 3
Потребно
сти
№1
№2
№3
№4
№5
2
8
9
60
3
5
8
70
4
1
4
120
2
4
7
130
4
1
2
100
Сумма запасов поставщиков совпадает с суммарным
спросом потребителей.
140+180+160=60+70+120+130+100=480, таким
образом, имеем задачу закрытого типа.
12
Запасы
140
180
160
480/480
13. Начальный план по методу северо-западного угла
Начальный план по методу северозападного углаДороги
№1
Карьер
Карьер 1 2
60
Карьер 2 8
Карьер 3 9
Потребно
60
сти
/
0
№2
3
5
8
70
70
/0
№3
4
1
4
10
11
120 0
/0
/
110
№4
2
4
7
№5
70
130
60
/60 /0
4
1
2
100
10
0
/0
Запасы
140
/80/ /0
180 10
/ /0
160
70
480
/
/0
100
Найдем затраты на перевозки при составленном плане:
F=2·60+8·0+9·0+3·70+5·0+8·0+4·10+1·110+4·0+2·0+4·70+7·60+4·0
+1·0+2·100=1380 у.д.е.
13
14. Начальный план по методу минимальных цен
ДорогиКарьер
№1
Карьер 1
2
Карьер 2
Карьер 3
Потребнос
ти
№2
№3
3
4
8
5
1
9
8
60
60/0
70
70/0
4
№4
2
12
0
120
/0
80
4
7
№5
130
/50/0
140/80/0
4
1
50
Запасы
2
180/ /0
60
40 160/120/ /0
70
100
/ /0 480
40
60
Найдем затраты на перевозки при составленном плане:
F=2·60+2·80+1·120+1·60+8·70+7·50+2·40=1450 у. д. е.
14
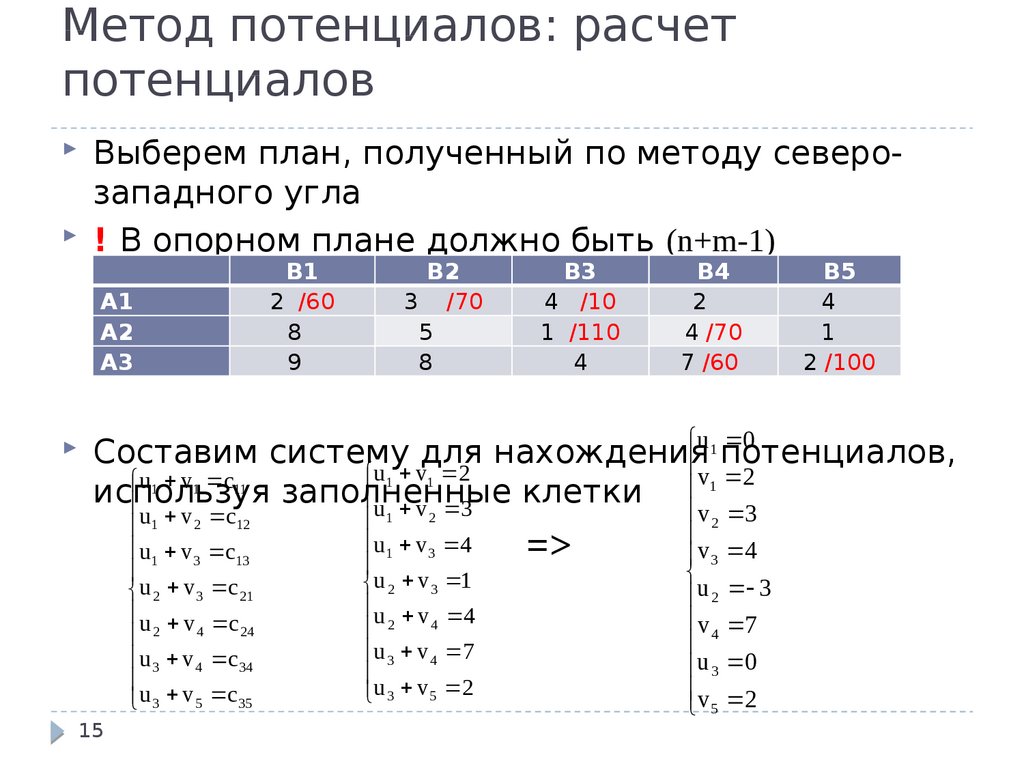
15. Метод потенциалов: расчет потенциалов
Выберем план, полученный по методу северозападного угла! В опорном плане должно быть (n+m-1)
B1
B2
B3
B4
B5
положительная
координата
А1
А2
А3
2 /60
8
9
3
/70
5
8
4 /10
1 /110
4
2
4 /70
7 /60
4
1
2 /100
u1 0
Составим систему для нахождения
v потенциалов,
u
v
2
1
1
u1 v1 c11
1 2
используя
заполненные
клетки
u v 3
u1 v 2 c12
u1 v 3 c13
u 2 v 3 c 21
u v c
4
24
2
u 3 v 4 c 34
u 3 v 5 c 35
15
2
1
u1 v 3 4
u 2 v 3 1
u v 4
4
2
u 3 v 4 7
u 3 v 5 2
=>
v 2 3
v 3 4
u 2 3
v 4 7
u 3 0
v 2
5
16. Метод потенциалов: оценка полученного плана
Рассчитаем оценки для всех свободныхПотенциал
B2
B3
B4
B5
клеток B1
ы
поставщик
ов
А1
А2
А3
2 /60
8
9
v1 =2
3
/70
5
8
v2=3
4 /10
1 /110
4
v3=3
Потенциал
d14 u1 v1 c14 0 7 2 5
ы
d u v c 0 2 4 2
потребител
1
5
15
15
ей
d 21 u 2 v1 c 21 3 2 8 9
d 22 u 2 v 2 c 22 3 3 5 5
d 25 u 2 v 5 c 25 3 2 1 2
d 31 u 3 v1 c 31 0 2 9 7
d 32 u 3 v 2 c 32 0 3 8 5
d u v c 0 3 7 4
1
5
15
33
16
2
4 /70
7 /60
v4=7
4
1
2 /100
v5=2
u1 =0
u2 =-3
u3 =0
=> (1,4) – клетка пересчета
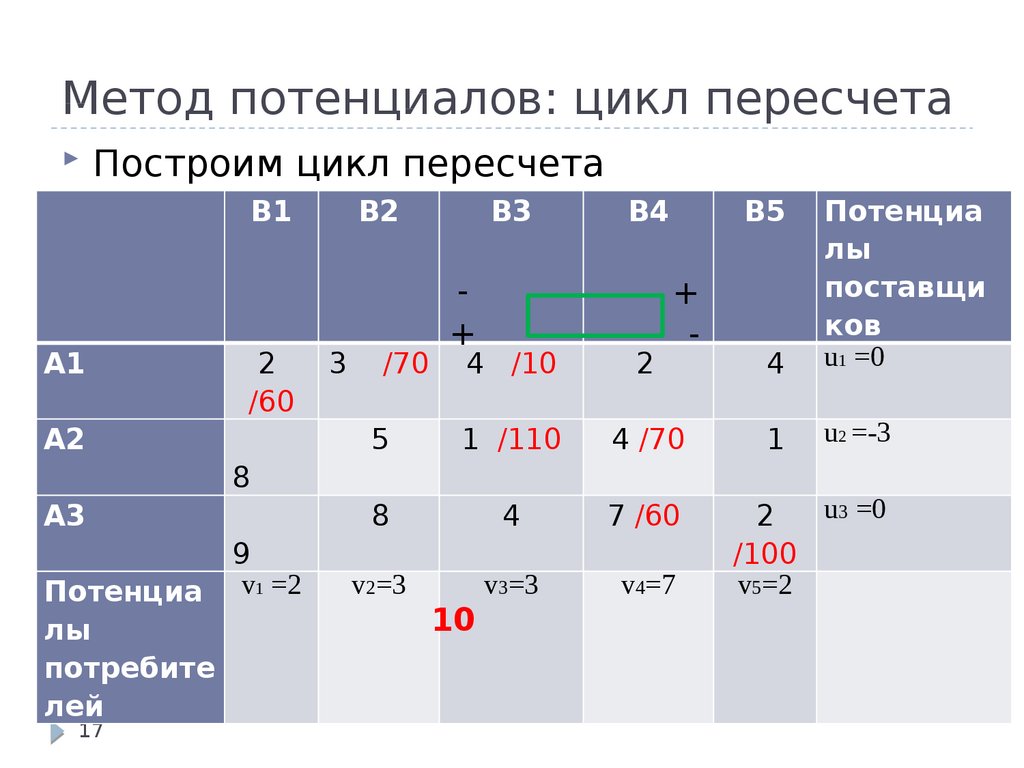
17. Метод потенциалов: цикл пересчета
Построим цикл пересчетаB1
А1
2
/60
А2
B2
3
/70
5
8
B3
+
B4
B5
+
-
4 /10
2
1 /110
4 /70
4
Потенциа
лы
поставщи
ков
u1 =0
1
u2 =-3
u3 =0
А3
8
4
7 /60
2
Определим наименьшею
поставку,
9
/100
стоящую
в отрицательных
v1 =2
v2=3
v3=3
vклетках,
4=7
v5=2 это
Потенциа
10
лы величину будем перераспределять
потребите
лей
17
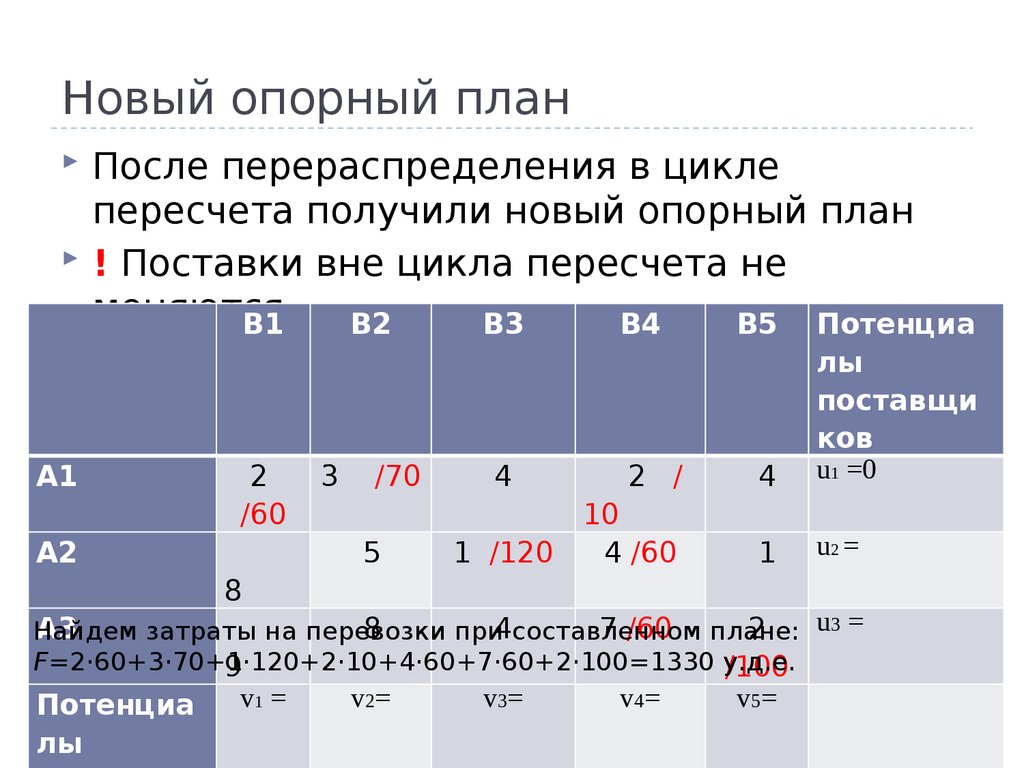
18. Новый опорный план
После перераспределения в циклепересчета получили новый опорный план
! Поставки вне цикла пересчета не
меняются
B1
B2
B3
B4
B5 Потенциа
А1
2
/60
А2
3
/70
5
4
1 /120
2 /
4
лы
поставщи
ков
u1 =0
10
4 /60
1
u2 =
8
u3 =
А3
8
7 /60 плане:
2
Найдем
затраты на перевозки
при4составленном
F=2·60+3·70+1·120+2·10+4·60+7·60+2·100=1330
у.д.е.
9
/100
Потенциа
18
лы
v1 =
v2=
v3=
v4=
v5=
19.
19Задание на
практику:
рассчитать
потенциалы и
оценки
для полученного















 mathematics
mathematics programming
programming








