Similar presentations:
Транспортная задача линейного программирования
1. Транспортная задача линейного программирования
Запасы: (ед.)А1=90
А2=260
А3=240
Потребности: (ед.)
В1=130
В2=150
В3=140
В4=170
Стоимость (руб.)
2 4 7 11
3 5 9 12
6 1 10 8
2. ШАГ 1 Проверка на сбалансированность
• Общее число запасов на складах:A
B
i,j
i,j
90 260 240 590ед.
130 150 140 170 590ед.
590 ед.=590 ед.
Задача является сбалансированной
(закрытого типа)
3. ШАГ 2 Отыскание начального решения. Метод северо-западного угла
В1=130 В2=150 В3=140 В4=170А1=90
2
4
7
11
90
А2=260
3
5
9
12
260
А3=240
6
1
10
8
240
130
150
140
170
4.
В1=130 В2=150 В3=140 В4=170А1=90
2
4
7
11
90
А2=260
3
5
9
12
260
А3=240
6
1
10
8
240
130
150
140
170
X11=min (90;130)=90
5.
В1=130А1=90
2
90
В2=150
4
X
В3=140
7
X
В4=170
11
90X
90=0
А2=260 3
5
9
12
260
А3=240 6
1
10
8
240
130-90=40
150
140
170
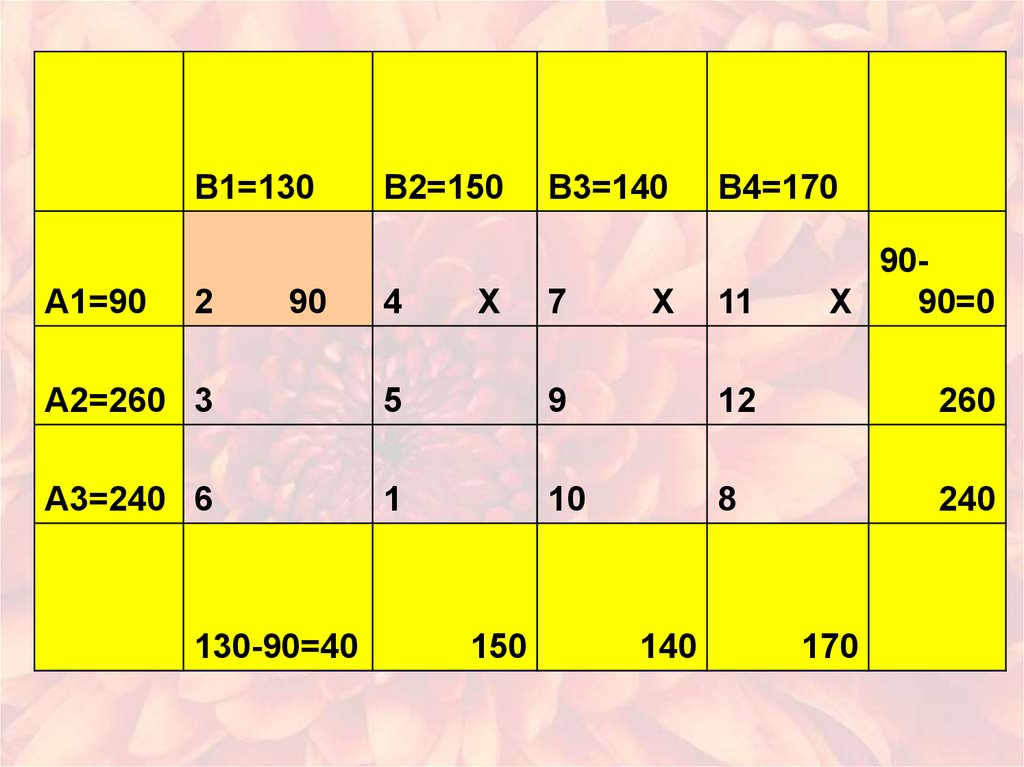
6. X21=min(40;260)=40
А1=90В1=130
В2=150
В3=140 В4=170
2
4
7
А2=260 3
90
40
А3=240 6
40-40=0
X
X 11
5
9
12
1
10
8
150
140
X
0
26040=220
240
170
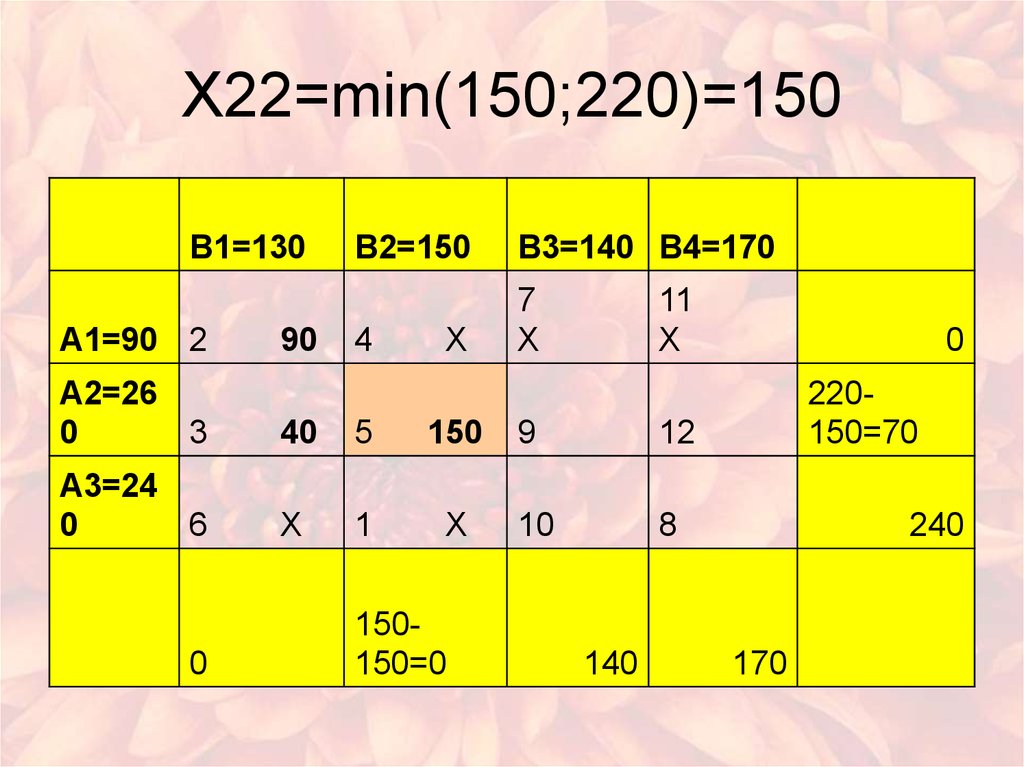
7. X22=min(150;220)=150
В1=130А1=90 2
90
В2=150
В3=140 В4=170
4
7
X
X
11
X
А2=26
0
3
40
5
150
9
12
А3=24
0
6
X
1
X
10
8
0
150150=0
140
0
220150=70
240
170
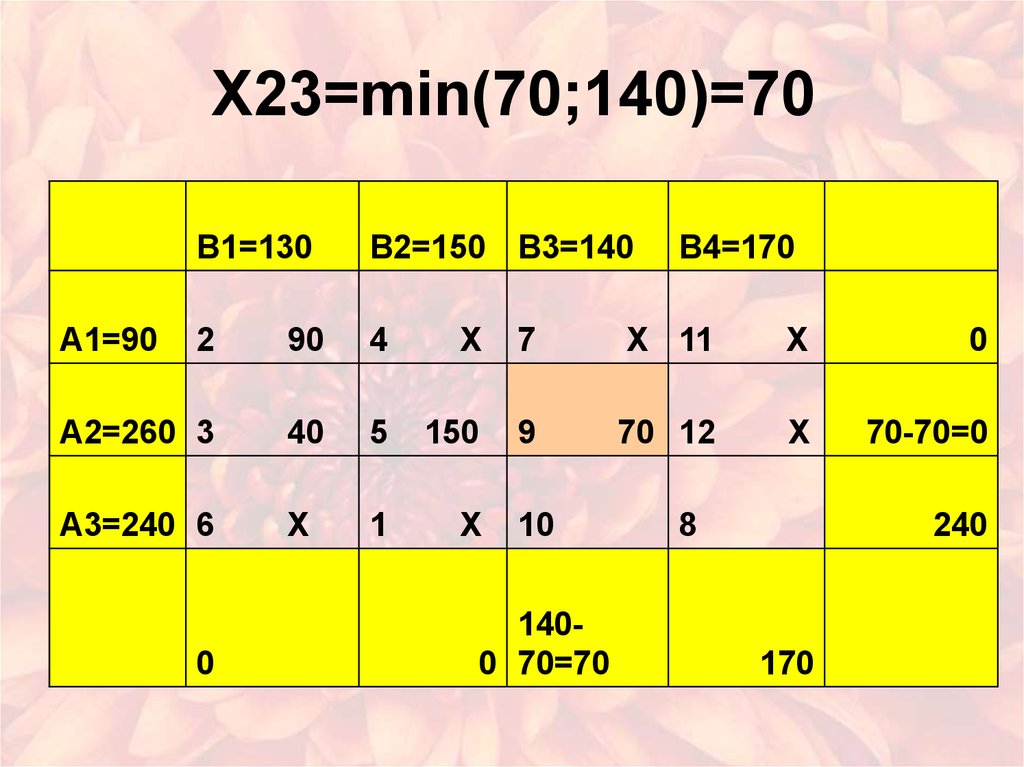
8. X23=min(70;140)=70
В1=130В2=150 В3=140
2
90
4
X
7
X 11
X
0
А2=260 3
40
5
150
9
70 12
X
70-70=0
А3=240 6
X
1
X
А1=90
0
10
1400 70=70
В4=170
8
240
170
9. X33=min(70;240)=70
В1=130В2=15
0
А1=90
2
90
4
X 7
X 11
X
0
А2=26
0
3
40
5
150 9
70 12
X
0
А3=24
0
6
0
X
1
В3=140
X 10
В4=170
24070=170
70 8
0 70-70=0
170
10. X34=min(170;170)=170
А1=90В1=130
В2=150 В3=140
2
4
90
X 7
В4=170
X 11
X
0
12
X
0
9
А2=260 3
40
5
150
70
10
А3=240 6
0
X
1
X
0
70
8
170170
170=0
1700
170=0
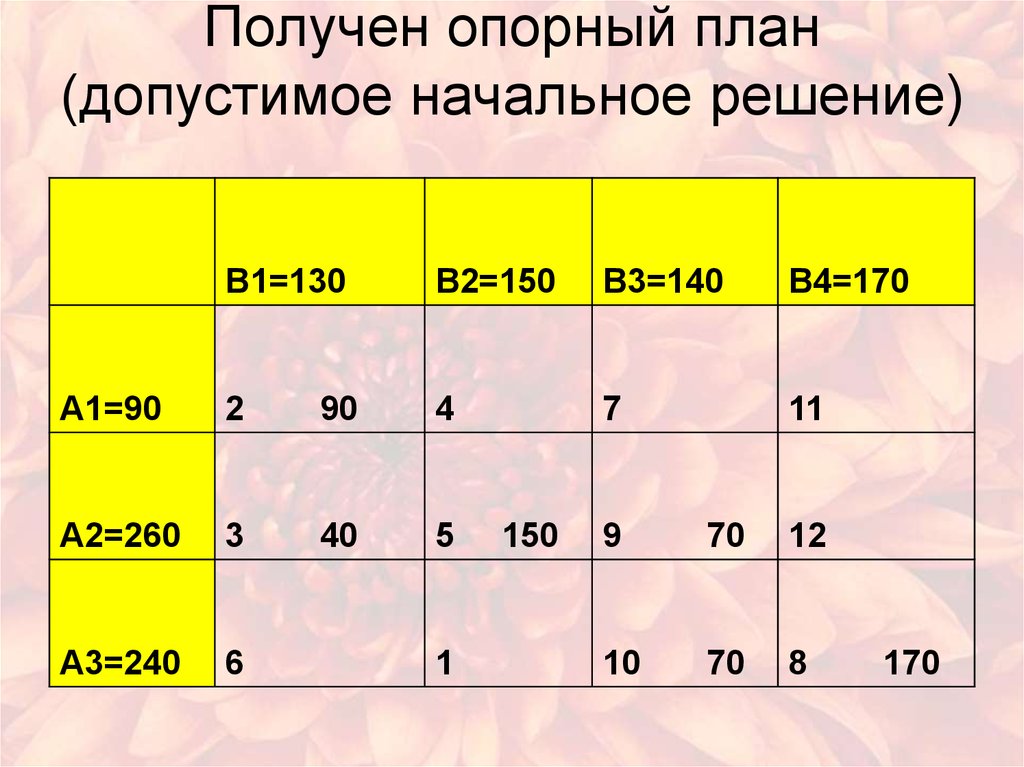
11. Получен опорный план (допустимое начальное решение)
В1=130В2=150
В3=140
В4=170
А1=90
2
90
4
7
11
А2=260
3
40
5
А3=240
6
1
150
9
70
12
10
70
8
170
12. Общие затраты на перевозку всей продукции:
F 2 90 3 40 5 1509 70 10 70 8 170
3740 руб.
13. Метод потенциалов
• U – строки• V – столбцы
• Вычисляем для занятых
клеток потенциалы строк и
столбцов
14.
V1V2
U1
2
90
4
U2
3
40
5
U3
6
1
V3
V4
7
150
11
9
70
12
10
70
8
170
15.
V1-U1=2;V1-U2=3;
V2-U2=5;
V3-U2=9;
V3-U3=10;
V4-U3=8.
пусть U1=0 тогда
V1=2;
U2=-1;
V2=4;
V3=8;
U3=-2;
V4=6.
16.
• Вычисляем оценку a(ij)для свободных клеток
• Она показывает на сколько
изменяются общие
транспортные затраты при
загрузке клетки продукцией.
17.
V1V2
U1
2
90
4
U2
3
40
5
U3
6
1
V3
V4
7
150
11
9
70
12
10
70
8
170
18.
(4) a12=V2-U1-C12=4-0-4=0;(7) a13=V3-U1-C13=8-0-7=1;
(11) a14=V4-U1-C14=6-0-11=-5;
(12) a24=V4-U2-C24=6+1-12=-5;
(6) a31=V1-U3-C31=2+2-6=-2;
(1) a32=V2-U3-C32=4+2-1=5
т.к. среди aij есть >0, то
план можно улучшить
19.
Выбираем наибольшееположительное значение
a(ij)
(1) a32=V2-U3-C32=4+2-1=5
с этой клетки a32 начинаем
цикл пересчета.
20.
• Цикл пересчета –замкнутая ломанная
линия, которая соединяет
начальную вершину и
занятые клетки.
• Начальная вершина
обозначается знаком “+”
21.
• 1)• Допустимые циклы:
2)
3)
22.
V1V2
U1
2
90
4
U2
3
40
5
U3
6
1
V3
V4
7
150
11
9
70
12
10
70
8
170
23.
• Находим минимальнуюпоставку отмеченную “-”
(70).
• Это значение вычитаем из
вершин цикла отмеченные
“+” и прибавляем к “-”
24.
V1V2
V3
7
V4
U1
2
90
4
U2
3
40
5 150-70 9 70+70
12
U3
6
1
8
+70 10 70-70
11
170
25. Получен план:
V1V2
V3
V4
U1
2
90
4
7
11
U2
3
40
5
80
9
140
12
U3
6
1
70
10
0
8
170
26. Стоимость полученного плана:
F 2 90 3 40 5 809 140 1 70 8 170
3390 руб.
27.
Проверим план на оптимальность.Для занятых клеток:
пусть U1=0 тогда
V1-U1=2;
V1=2;
V1-U2=3;
U2=-1;
V2-U2=5;
V2=4;
V3-U2=9;
V3=8;
V2-U3=1;
U3=3;
V4-U3=8.
V4=11.
28. Оценка для свободных клеток:
(4) a12=V2-U1-C12=4-0-4=0;(7) a13=V3-U1-C13=8-0-7=1;
(11) a14=V4-U1-C14=11-0-11=0;
(12) a24=V4-U2-C24=11+1-12=0;
(6) a31=V1-U3-C31=2-3-6=-7;
(10) a33=V3-U3-C33=8-3-10=-5
т.к. среди aij есть >0, то план
можно улучшить
29. наибольшее значение:
(7) a13=V3-U1-C13=8-0-7=1;a13 вершина цикла
пересчета
30.
V1V2
U1
2
90
4
U2
3
40
5
U3
6
1
V3
V4
7
11
80
9
140 12
70
10
8
170
31.
V1V2
U1
2
90-90
4
U2
3
40+90
5
V3
7
80
9
+90
V4
11
140-90 12
8
U3
6
1
70
10
170
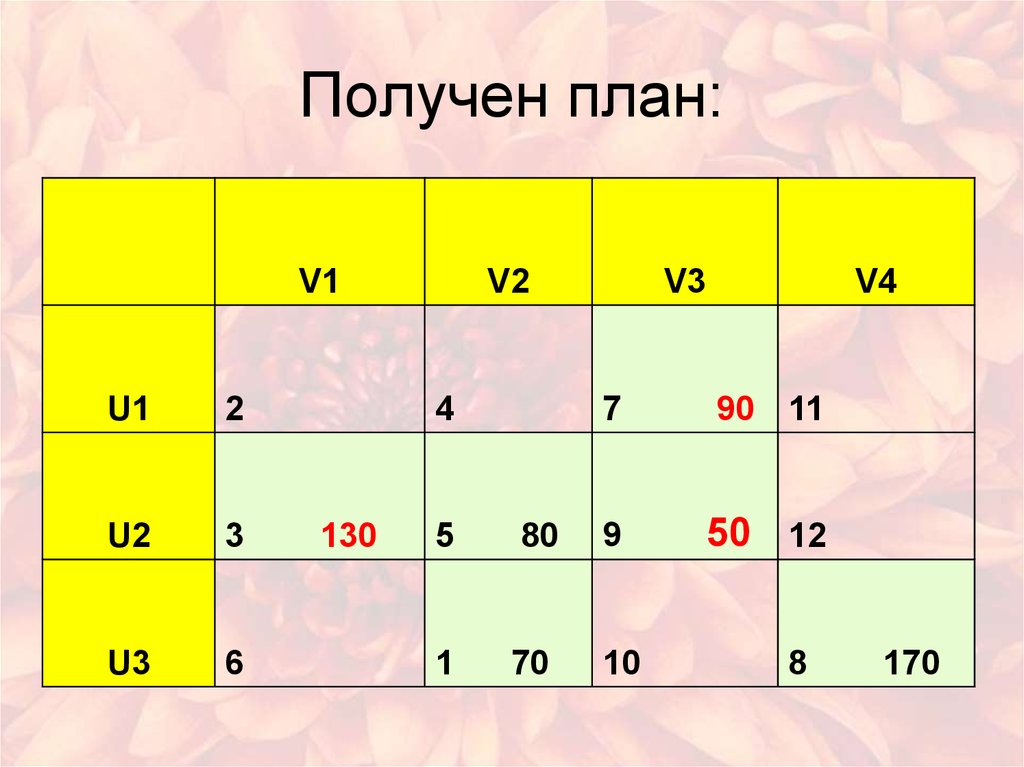
32. Получен план:
V1U1
2
U2
3
U3
6
V2
4
130
V3
V4
7
90 11
50 12
5
80
9
1
70
10
8
170
33. Стоимость полученного плана:
F 7 90 3 130 5 809 50 8 170 1 70
3300 руб.
34.
Проверим план на оптимальность.Для занятых клеток:
пусть U1=0 тогда
V3-U1=7;
V3=7;
V1-U2=3;
U2=-2;
V2-U2=5;
V1=1;
V3-U2=9;
V2=3;
V2-U3=1;
U3=2;
V4-U3=8.
V4=10
35. Оценка для свободных клеток:
(4) a12=V2-U1-C12=3-0-4=-1;(11) a14=V4-U1-C14=10-0-11=-1;
(2) a11=V1-U1-C11=1-0-2=-1;
(12) a24=V4-U2-C24=10+2-12=0;
(6) a31=V1-U3-C31=1-2-6=-7;
(10) a33=V3-U3-C33=7-2-10=-8
т.к. aij <0, то план улучшить
НЕЛЬЗЯ
36. Оптимальное решение:
Fопт 7 90 3 130 5 809 50 8 170 1 70
3300 руб.































 programming
programming








