Транспортная задача. Лекция 6

1. ТРАНСПОРТНАЯ ЗАДАЧА

Лекция 6

2.

Транспортная задача - частный случай задачи
линейного программирования и может быть
решена симплекс-методом. Однако, в силу
особенностей она решается с помощью
распределительного метода и его модификаций

3.

Общая постановка транспортной задачи
состоит в определении оптимального плана
перевозок некоторого однородного груза из m
пунктов отправления А1, А2,…, Аm в n пунктов
назначения B1, B2,…,Bn.
При этом в качестве критерия оптимальности
берется либо минимальная стоимость перевозок
всего груза, либо минимальное время его
доставки.

4.

Рассмотрим транспортную задачу, в которой в
качестве критерия оптимальности берется
минимальная стоимость перевозок всего груза.
Обозначим через cij тарифы или стоимости
перевозки единицы груза из i-го пункта
отправления в j-й пункт назначения, через ai –
запасы груза в i-м пункте отправления,
через b j – потребности в грузе j-ым пунктом
назначения, через xij– количество единиц груза,
перевозимого из i-го пункта отправления в j-й
пункт назначения (перевозки).

5. Математическая модель транспортной задачи

Найти
m
n
F cij xij min
i 1 j 1
при ограничениях
xij b j , j 1, n
i 1
n
xij ai , i 1, m
j 1
x 0
ij
m

6.

Первое ограничение
xij b j , j 1, n
i 1
m
означает, что все потребности должны быть
удовлетворены , а второе -
n
xij ai , i ,1, m
j 1
что все запасы должны быть перевезены.

7.

Определение. Всякое неотрицательное решение
системы ограничений транспортной задачи,
определяемое матрицей размера m×n
x11 x12 ...x1n
x
x
...
x
21
22
2n
X
,
.................
xm1 xm 2 ...xmn
называют допустимым решением (или планом)
транспортной задачи.

8.

Определение.
План
,
ij m n
X (x )
при котором целевая функция принимает
минимальное значение, называется
оптимальным.

9.

Тарифы или стоимости перевозок единицы груза
сij также задаются матрицей, которая называется
матрицей транспортных издержек или матрицей
стоимостей
c11c12 ...c1n
c
c
...
c
21
22
2n
C
.................
cm1cm 2 ...cmn

10. Транспортная таблица

11. Необходимое и достаточное условие разрешимости транспортной задачи

Для разрешимости транспортной задачи
необходимо и достаточно, чтобы запасы груза в
пунктах отправления были равны потребностям в
грузе в пунктах назначения, то есть, чтобы
выполнялось равенство:
m
n
a b
i 1
i
j 1
j
балансовые условия

12.

При выполнении этого условия модель
транспортной задачи называется закрытой.
Если балансовое условие не выполняется, то
модель транспортной задачи называется
открытой.
В случае открытой транспортной задачи выполнение балансового
условия достигается введением фиктивного поставщика или
фиктивного потребителя с соответствующими тарифами, равными
нулю.

13.

Любое решение транспортной задачи
представляет собой распределение перевозок xij
в транспортной таблице.
Оптимальному решению транспортной задачи
соответствует оптимальное распределение
перевозок.
Перераспределение перевозок в транспортной
таблице осуществляется до тех пор, пока не
будет найдено оптимальное распределение
перевозок.

14. Этапы решения транспортной задачи

Составляют математическую модель задачи.
Находят исходное опорное решение.
Проверяют это решение на оптимальность.
Переходят от одного опорного решения к
другому.

15. Пример

Компания контролирует три фабрики А1, А2, А3, способные
произвести 50, 25 и 25 тысяч изделий ежедневно.
Она заключила договоры с четырьмя заказчиками В1, В2, В3
и В4, которым ежедневно требуется 25, 20, 30 и 25 тысяч
изделий соответственно. Стоимости транспортировки 1 тысячи
изделий заказчикам с фабрик следующие:
Определить минимизирующую общую стоимость план
перевозок изделий от фабрик к заказчикам.

16. Составляем математическую модель задачи

Компания контролирует три фабрики А1, А2, А3, способные произвести 50,
25 и 25 тысяч изделий ежедневно.
Она заключила договоры с четырьмя заказчиками В1, В2, В3 и В4, которым
ежедневно требуется 25, 20, 30 и 25 тысяч изделий соответственно.
Пусть xijколичество изделий, перевозимых с i-й фабрики j-му заказчику

17. Составляем математическую модель задачи

Пусть cij стоимость перевозки с i-й фабрики j-му потребителю
матрица стоимостей
Найти матрицу перевозок Х, такую чтобы

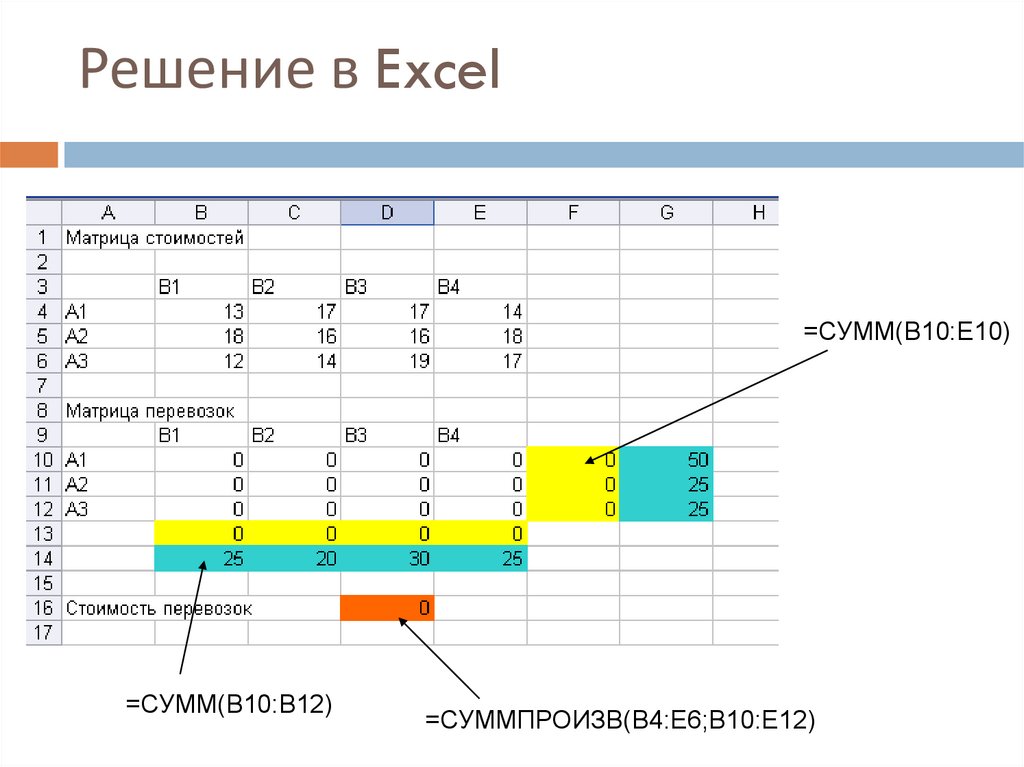
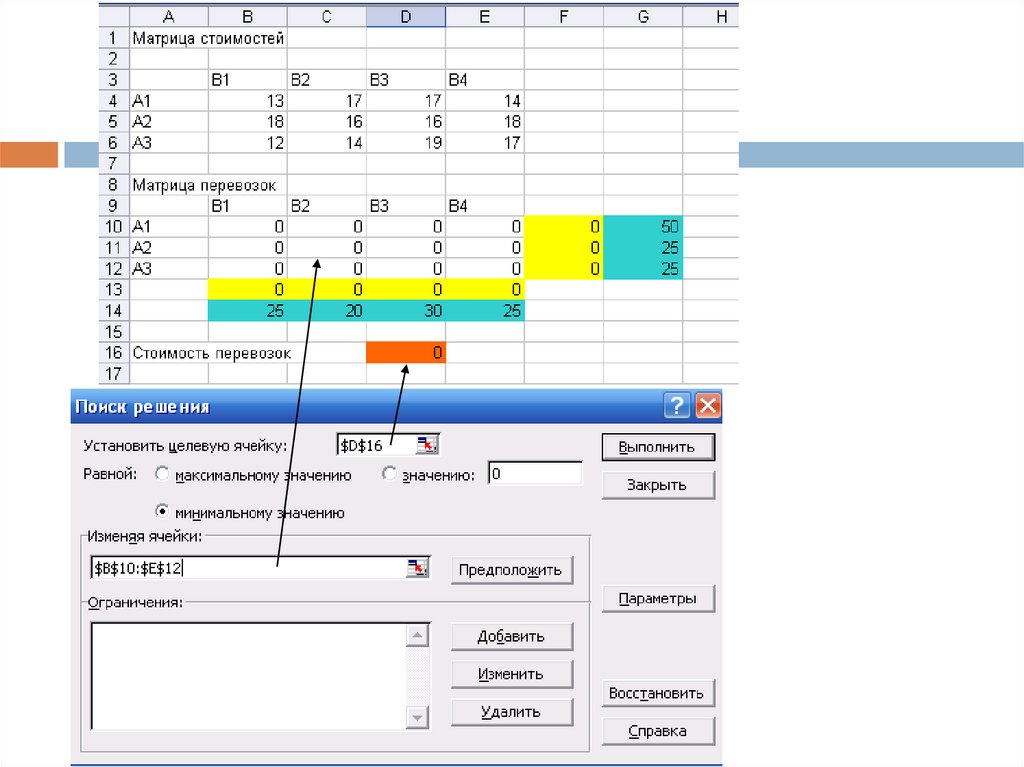
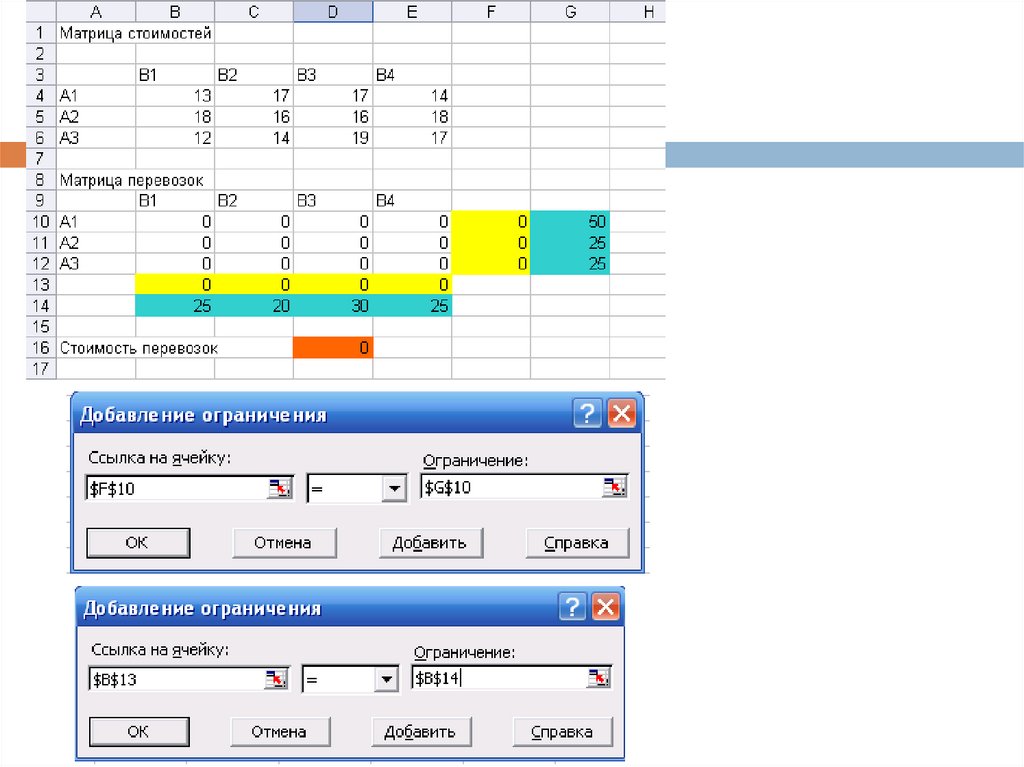
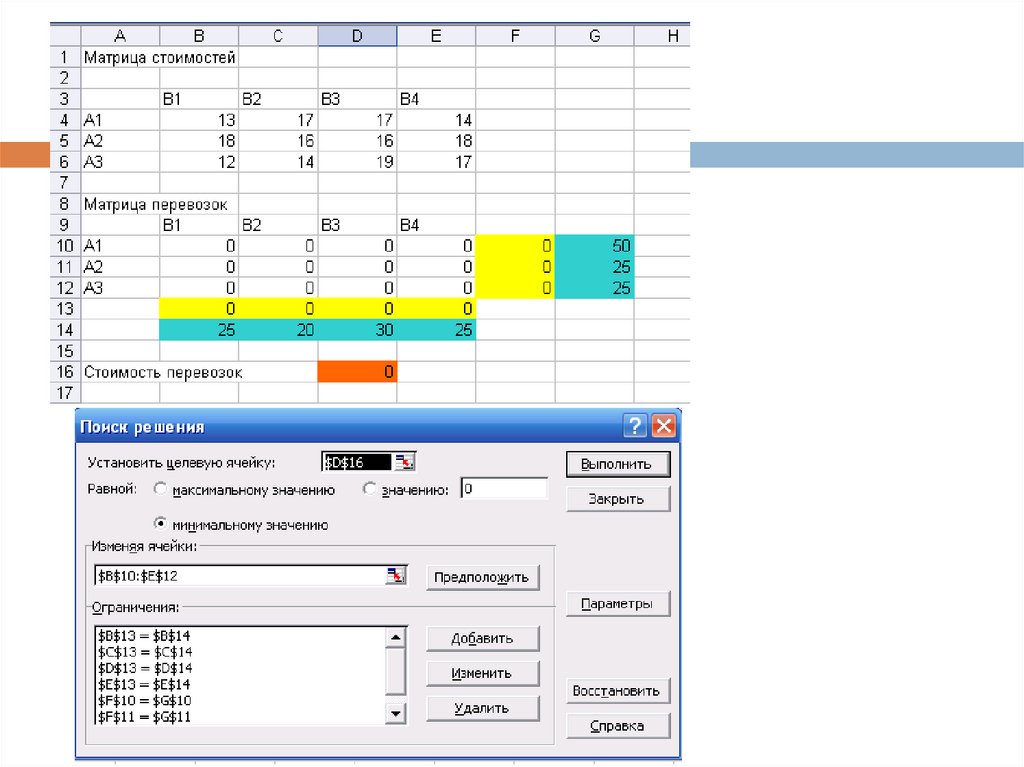
18. Решение в Excel

=СУММ(B10:E10)
=СУММ(B10:B12)
=СУММПРОИЗВ(B4:E6;B10:E12)