Similar presentations:
Экономический факультет. Транспортная задача. Лекция 6
1. Экономический факультет
Транспортная задача2.
План лекции1. Постановка и формализация транспортной задачи
2. Базовая модель транспортной задачи
3. Открытые и закрытые модели транспортной задачи
4. Общие свойства методов решения транспортной задачи
5. Метод потенциалов
6. Решение транспортной задачи с дополнительными
ограничениями
3.
На практике решаются в основномследующие задачи:
1. Найти оптимальную структуру
транспортных средств, обеспечивающую
минимизацию издержек на транспортировку;
2. Установить такое распределение грузов
между имеющимися в хозяйстве видами
транспорта, при котором затраты на
перевозки всего объёма грузов были бы
минимальными;
3. Задача прикрепления потребителей к
поставщикам.
3
4.
Первая постановка задачи обусловливаетсятем, что эксплуатационные и экономические
показатели зависят от состава транспорта, а
вторая – когда эффективность использования
различного транспорта на одной и той же
работе не всегда одинакова.
Это классическая транспортная задача. С неё
начиналось математическое
программирование.
4
5.
Известно около двух десятков постановоктранспортной задачи. Это самостоятельные
экономические, хозяйственные задачи.
Но в своей основе они имеют один тип
моделей, однако, конкретные ситуации иногда
сильно отличаются друг от друга.
5
6.
В качестве критерия оптимизации чаще другихиспользуются следующие:
1. Минимум денежно-материальных затрат на
перевозки;
2. Минимум затрат времени на перевозки;
3. Минимум объема транспортных работ;
4. Минимум приведенных затрат.
6
7.
Первый критерий учитывает эффективность перевозок,используется чаще других. Рассчитывается путем
умножения себестоимости перевозок на объемы.
Иногда вместо себестоимости, применяют тарифные
стоимости, тарифы.
Если перевозки выполняются привлечённым
транспортом, расчёт ведётся по тарифной сетке на
договорной основе. Технически расчёт сводится к
умножению тарифа на объём перевозок. Наличие в
сельском хозяйстве скоропортящихся грузов иногда
требует кратчайших перевозок по времени. Это можно
достигнуть минимизировав затраты времени на
перевозки.
7
8.
Минимум приведённых затрат наиболее полноучитывает все затраты, связанные не только с
перевозками, но и с приобретением транспортных
средств, то есть с учётом капиталовложений.
8
9.
Первый общий метод решения транспортнойзадачи, получивший название «метода
потенциалов» предложен Л.В. Канторовичем.
В наиболее общем виде транспортная задача
может быть поставлена так: Требуется найти
наиболее экономичный план перевозок от
поставщиков к потребителям.
9
10.
Формализация задачиm – количество пунктов отправления (поставщики),
i – номер поставщика,
n – количество пунктов назначения (потребители),
j – номер потребителя,
аi – объем однородного груза i-го поставщика (запас),
вj – объем однородного груза, требуемого j-ому
потребителю (спрос)
сij – стоимость доставки единицы груза i-го
поставщика j-ому потребителю
хij – количество груза, доставляемое от i-го
поставщика к j-ому потребителю
С – общие затраты на перевозки.
11.
Используя эти формализованные характеристики,можно составить матрицу перевозок. По строкам
размещаются поставщики, по столбцам –
потребители. На пересечении строк и столбцов
указывается стоимость доставки единицы груза от
i-го поставщика к j-му потребителю. Здесь же
представляется количество доставленного груза.
Используя данную схему, можно записать
математическую модель транспортной задачи в
структурной, компактной форме
12.
Таблица – Схема матрицы перевозокПотребитель
Поставщик
1
…
i
…
m
Спрос
1
…
j
c11 …
…
c1j …
n
Запас
c1n
а1
x11
x1j
x1n
… …
…
…
…
ci1
cij
cin
xi1
xij
xin
… …
…
…
…
cm1
cmj
cmn
xm1
xmj
xmn
в1
…
вj
…
вn
…
аi
…
аm
m
n
i 1
j 1
аi в j
13.
Стоимость перевозок можно выразитьследующим образом:
С= с11х11 + … + сijxij + … cmnxmn min
или более компактно
m
n
i 1
j 1
С= cij xij min
14.
Это целевая функция, она позволяетопределить численное значение критерия
оптимальности на всех этапах расчетов и в
оптимальном плане. Требуется найти
минимальное значение целевой функции
при условиях:
15.
1. Условие вывоза всего груза от каждогопоставщика:
х11+…+хij+…x1n = a1
------------------------xi1+…+xij+…+xin = ai
------------------------xm1+…xmj+…+xmn = am
Или более компактно:
n
x a
j 1
ij
i
где i = 1…m;
16.
2. Условие выполнения спроса каждогопотребителя:
х11+…+хi1+…xm1=в1
------------------------x1j+…+xij+…+xmj = вj
------------------------x1n+…xin+…+xmn = вn
или более компактно
m
х в
i 1
ij
j
, где j=1…n
17.
3. Условие равенства запаса и спроса:а1+…аi+…am=в1+…+вj+…вn
или более компактно:
m
n
а в
i 1
i
j 1
j
4. Условие неотрицательности переменных:
хij 0
17
18.
В линейном программировании доказываетсячто: Равенство запаса и спроса есть
необходимое и достаточное условие
совместимости, следовательно,
разрешимости транспортной задачи.
Это базовая модель транспортной задачи. На
ее основе решаются многие
оптимизационные задачи.
18
19.
Модель, у которой запас и спросравны, называется закрытой. Задача
тоже называется закрытой.
Модель, у которой запас и спрос не
равны, называется открытой.
Возможны два случая:
19
20.
Первый случай. Запас превышает спросМодель будет иметь вид:
m
n
i 1
j 1
С cij xij min
При условиях:
n
1.
xij ai
j 1
где i = 1…m;
То есть не требуется весь имеющийся груз
вывозить от поставщика, после удовлетворения
спроса часть его может остаться не вывезенной
20
21.
m2.
x в
ij
i 1
где j = 1…n.
j
Потребности (спрос) каждого потребителя
необходимо выполнить полностью.
m
3.
n
а в - запас превышает спрос
i 1
i
j 1
j
4. хij 0 - условие неотрицательности
переменных
22.
Для решения этой задачи в матрицуперевозок вводится фиктивный
потребитель. Его спрос определяют как
разность запаса и спроса всех поставщиков
и потребителей, то есть:
m
n
а в в
i 1
i
j 1
j
n 1
22
23.
Стоимость доставки фиктивномупотребителю принимается за нуль, так как в
действительности эти перевозки
осуществляться не будут. Введением
фиктивного потребителя открытая модель
преобразуется в закрытую.
23
24.
Второй случай. Спрос превышает запас.Модель имеет вид:
m
n
i 1
j 1
С cij xij min
При условиях:
n
1.
x a
j 1
ij
i
где i = 1…m;
24
25.
m2.
x в
i 1
ij
где j = 1…n;
j
Спрос не всех потребителей будет выполнен.
n
3.
в a - спрос превышает запас,
j 1
4.
m
j
i 1
i
хij 0
25
26.
В этой задаче спрос превышает запас и вмодель вводится фиктивный поставщик. Его
запас определяется как разность спроса и
запаса всех потребителей и поставщиков:
n
m
в a a
j 1
j
i 1
i
m 1
26
27.
Иногда в такой модели предусматриваютсяусловия, при которых спрос особо важных
потребителей удовлетворялся возможно
полнее, несмотря на то, что запас
поставщиков не может удовлетворить спрос
всех потребителей.
Тогда в модель задачи вводятся
дополнительные условия и характеристики.
27
28.
nС cij xij l j z j min, max
i 1 j 1
j 1
m
n
По экономическому смыслу второе
слагаемое может быть сумма штрафа или
неустойки за недопоставку грузов.
Такую задачу называют транспортной с
блокировкой перевозок.
28
29.
При изучении любого метода решениязадачи важно понять логику его алгоритма.
Обычно она включает три момента:
1. Получение начального плана,
называемого опорным планом;
2. Оценка плана по критерию
оптимальности, который показывает
можно ли улучшить план;
3. Совершенствование опорного плана и
получение оптимального (или близкого
к оптимальному) плана.
29
30.
При изучении методов решениятранспортной задачи необходимо
помнить ее специфику, а именно:
1. Ограничения заданы уравнениями, всего
m + n уравнений с m и n неизвестными
2. Каждое неизвестное входит только в два
уравнения. Неизвестное хij входит в
уравнение с правой частью аj и уравнение с
правой частью вj.
3. Коэффициенты в уравнениях являются
единицами.
30
31.
При любых значениях m и n втранспортной задаче независимыми
являются только (m+n-1) уравнений,
поэтому в оптимальном плане отличными
от нуля могут быть не более (m+n-1)
компоненты. Это относится и к
невырожденному опорному плану – он
тоже может иметь только (m+n-1)
положительных компонент или перевозок.
Решение транспортной задачи любым
способом при немашинном счете
выполняется на специальном макете.
31
32.
Метод потенциалов – один из наиболеераспространенных методов решения
транспортной задачи. Автор его – Л.В.
Канторович. В 1951 году американский
ученый Дж. Данциг предложил
модифицированный распределительный
метод. Этот метод лишь в деталях отличается
от метода потенциалов Канторовича, хотя и
появился на несколько лет позже.
Метод потенциалов свое название получил от
условных чисел – названных Канторовичем
потенциалами:
32
33.
Доказывается теорема:Если для некоторого плана транспортной
задачи можно набрать систему из m + n
чисел
u1, u2,…ui, …um;
v1, v2,…vj, …vn;
удовлетворяющим условиям
vj + ui = cij
при хij > 0,
vj + ui ≤ cij
при хij = 0,
то план оптимальный.
33
34.
Выражение vj + ui = cij при хij >0 можнообъяснить так: для поставщиков и
потребителей, между которыми
запланированы перевозки, сумма
потенциалов совпадает с затратами на
транспортировку единицы груза.
Выражение vj + ui ≤ cij при хij =0 означает, что
для всех остальных пар поставщиков и
потребителей, между которыми перевозки
не запланированы, суммы потенциалов не
превосходят затрат по транспортировке.
34
35.
Это утверждение принимается в качествепризнака оптимальности плана.
Числа vj – называются потенциалами
потребителя, а ui – потенциалами
поставщика.
35
36.
Экономический смысл потенциалов сводится кследующему. Если план перевозок оптимален, то
можно присвоить грузам в пунктах отправления и
пунктах назначения потенциалы, при которых
перевозка из любого пункта отправления в любой
пункт назначения не могла бы дать «прибыль»
(учитывая, что оценка груза в любом пункте
потребления не должна превышать оценки его в
любом пункте производства с учетом расходов на
перевозки), и чтобы в тоже время перевозки,
внесенные в план, являлись безубыточными
(оценка груза в пункте производства плюс издержки
по его перевозке должны в точности покрываться
оценкой груза в пункте потребителя).
36
37.
Построение опорного планаСуществует различные способы
построения опорного плана
транспортной задачи. Чаще других
используют:
1. Способ северо-западного угла,
2. Способ наилучших тарифов,
3. Способ двойного предпочтения.
37
38.
1-й способ. Не учитывая тарифов сij сверхнего левого угла, выполняются
потребности, начиная с меньшего числа.
Этот способ прост, но план строится без
учета оценок сij и он может оказаться
далеким от оптимального. Способ северозападного угла удобен при вычислениях на
ЭВМ.
38
39.
Суть способа наилучших тарифов состоитв том, что из матрицы выбирается клетка с
наименьшей стоимостью и заполняется
меньшим из чисел аi и вj. Затем из
рассмотрения исключают либо строку, либо
столбец, чей ресурс израсходован или
потребности удовлетворены. И так
повторяют до построения плана.
39
40.
Способ двойного предпочтения заключаетсяв следующем: в каждом столбце отмечается
клетка с наименьшим тарифом, после чего
аналогичные действия выполняются в
каждой строке. В результате некоторые
клетки будут отмечены дважды
(рассматриваются в первую очередь) или
один раз (рассматриваются по вторичному
критерию). Данный способ удобен при
построении опорного плана матриц больших
размерностей, в которых перебор тарифов
во всех клетках затруднителен при способе
наилучшего тарифа.
40
41.
Проверка плана на оптимальностьДля проверки плана на оптимальность
необходимо построить систему
потенциалов, определяемых по занятым
клеткам:
vj + ui = cij если хij > 0
откуда vj = cij – ui
или ui = cij – vj
41
42.
Систему потенциалов можно построитьтолько для невырожденного опорного
плана. Такой план содержит m+n-1 занятых
клеток. Существует несколько способов
преодоления вырождения опорного плана.
Самый простой из них состоит в том, что
одну из недостающих клеток считают
условно занятой с поставкой нуль. Такую
клетку считают фиктивно занятой.
Фиктивных клеток может быть несколько.
Обычно их выбирают так, чтобы можно было
рассчитать систему потенциалов.
42
43.
Расчет начинается с присвоения одному изпотенциалов произвольного значения. План
на оптимальность проверяется по
свободным клеткам матрицы по формуле:
vj + ui ≤ cij при хij = 0
43
44.
Улучшение плана путемперераспределения груза по циклу
Циклом называется набор клеток в цепи,
в котором только две соседние клетки
расположены в одном столбце или одной
строке, причем последняя находится в
той же строке или столбце, что и первая.
44
45.
В матрице перевозок цикл нагляднопредставлен контуром, для построения
которого свойственны правила:
1. Построение контура начинается и
завершается в неоптимальной
клетке;
2. Вершины контура могут быть
размещены в неоптимальной и
заполненных клетках;
3. Переходы контура строго
вертикальные и горизонтальные
45
46.
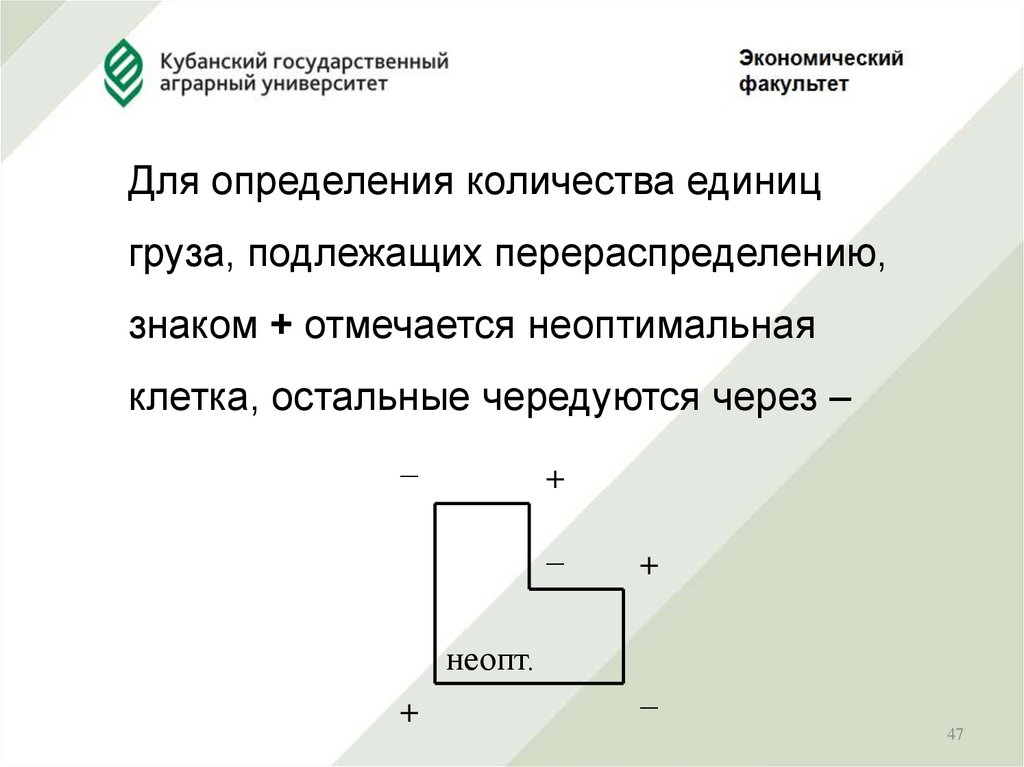
4647.
Для определения количества единицгруза, подлежащих перераспределению,
знаком + отмечается неоптимальная
клетка, остальные чередуются через –
−
+
−
+
неопт.
+
−
47
48.
Далее определяется вершина цикла сознаком минус, в которой определен
минимальный объем перевозок и он
последовательно вычитается из всех
объемов расположенных в отрицательных
вершинах и прибавляется к объемам в
вершинах помеченных знаком плюс.
48
49.
В результате этих действий клетка сминимальным объемом освобождается, а
избранная потенциальная клетка
загружается. Баланс объема груза при этом
не нарушается, но целевая функция
улучшается. Этот новый план принимается
за исходный, и расчеты повторяются до
получения оптимального плана. При этом
потенциалы необходимо пересчитывать,
так как система занятых и свободных
клеток изменилась.
49
50.
Методом потенциалов можно решатьтранспортные задачи и на max.
Проф. М.Е. Браславец, например,
рекомендует в этом случае переменить знак
у всех показателей критерия оптимальности
и решать задачу обычным способом на
минимум, а в результате будет получено
решение на максимум.
50
51.
Можно и непосредственно решатьтранспортную задачу на max, но при этом
распределение поставок производить не по
отрицательным, а по положительным
характеристикам клеток, оптимальное
решение получается тогда, когда все
характеристики свободных клеток будут
иметь отрицательные значения.
51
52.
1. Если по какому – то маршруту груз перевозитьнельзя, то в этой клетке тариф считается бесконечно
большим.
Тогда сумма потенциалов для этой клетки всегда
будет меньше тарифа, и условие на любом шаге
будет выполнено, и клетка до конца остается пустой.
2. Если по заданному маршруту должно быть
перевезено строго определенное количество груза,
то он заранее учитывается в клетке и в дальнейшем
она считается свободной с большим тарифом М. В
цикл она не включается и зафиксированная в ней
перевозка остается до конца.
52
53.
3. Если по маршруту необходимо перевезти груза неменее указанного количества, перевозку планируют
отдельно, вычитая из запаса и спроса данного
маршрута. Полученную новую задачу решают
обычным методом.
4. При ограничении перевозок сверху по пропускной
способности решение ведем обычным способом до
получения в клетке максимально допустимого числа.
После этого клетку считаем свободной с большим
тарифом.
53


















































 mathematics
mathematics