Скалярное произведение векторов. 9 класс

1. Скалярное произведение векторов. 9 класс

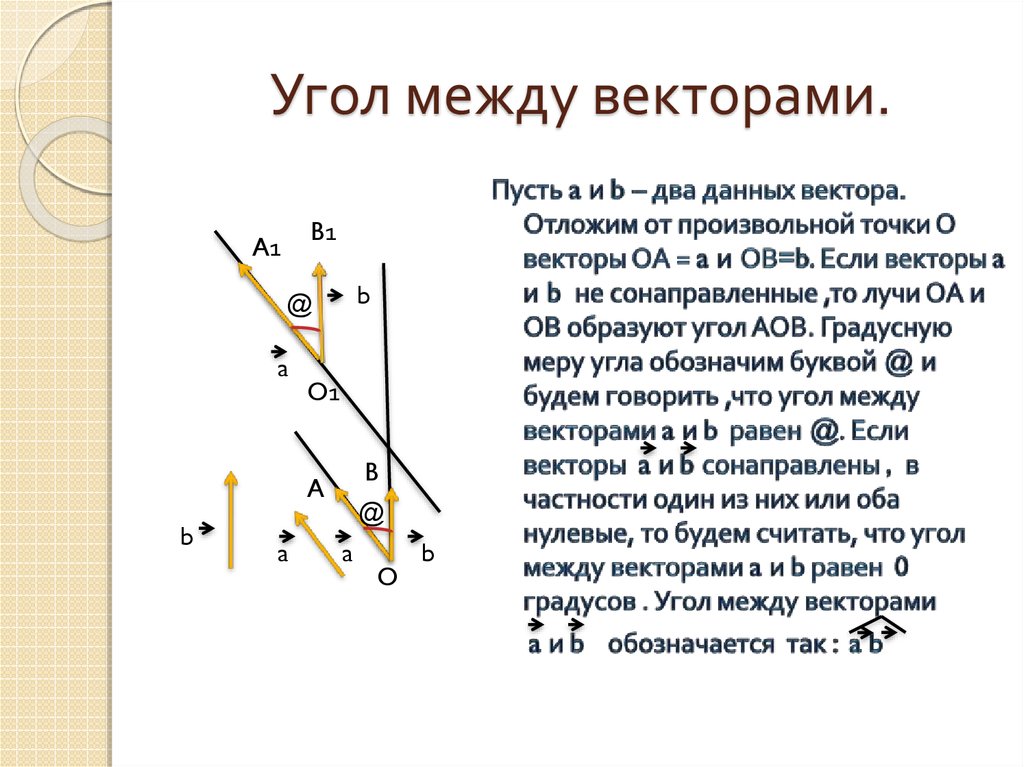
2. Угол между векторами.

B1
A1
b
@
a
O1
B
A
b
a
@
a
O
b

3. Угол между векторами.

a
30
c
d
b
f
Два вектора называются
перпендикулярными ,
если угол между ними
равен 90 градусов. На
рисунке b c , b d, b f.

4. Скалярное произведение векторов.

I Скалярное произведение двух
векторов называется
произведение их длин на
косинус угла между ними.
II Скалярное произведение
нулевых векторов равно нулю
тогда и только тогда ,когда
эти векторы перпендикулярны.
III Скалярное произведение a * a называется
скалярным квадратом вектора a и
обозначается a 2. Таким образом, скалярный
квадрат вектора равен квадрату его длинны.

5. Скалярное произведение в координатах.

Теорема
Скалярное произведение векторов
a {x1;y1} и b {x2; y2 } выражается
формулой a * b = x1 x2 + y1y.2

6. Скалярное произведение в координатах.

Следствие I
Нулевые векторы a {x
;y } и b {x2 ;y2}
1 1
перпендикулярны тогда и только тогда,
когда x1 x2 + y1y 2=0.
Следствие II
Косинус угла @ между ненулевыми векторами
a {x ;y } и b {x ;y } выражается формулой
1 1
2 2
cos @ =
x x +y y
1 2 1 2
2 2
x +y
1 1
*
x 2+ y2
2
2