849.77K

Category:

physics

Оптимальное обнаружение и различение сигналов с неизвестной начальной фазой. Тема 4: Часть 4

1. Тема 4:

Часть 4:
Оптимальное обнаружение и различение сигналов с
неизвестной начальной фазой.
Оптимальное различение двух полностью известных
сигналов

2.

Оптимальное обнаружение сигнала
(сигнал с неизвестной начальной фазой)
s , (t ) U (t ) cos 0t (t )
закон АМ
закон ФМ
Сигнал
Апостериорная вероятность параметра
1 2 q ( , )
0 p ps ( | )d 2 0 сe d e
Корреляционный интеграл:
1
p ps ( ) p ps ( | )w pr ( )d
2
0
2
T
Ec ( )
G0
p pr ( )
T
2
2
q( , )
y
(
t
)
s
(
t
)
dt
y (t ) U (t )cos 0 (t ) dt
,
G0 0
G0 0
2
2
1
q ( , )
e
d
I
Z
(
)
0
2 0
G
0
T
Z c ( ) y (t ) U (t )cos 0t (t ) dt
0
Z ( ) Z c ( ) 2 Z s ( ) 2
T
Z s ( ) y (t ) U (t )sin 0t (t ) dt
0

3.

Оптимальное обнаружение сигнала
(сигнал с неизвестной начальной фазой)
Апостериорная вероятность параметра
2
p ps ( ) сI 0 Z ( ) e
G0
1
Ec ( )
G0
p pr ( )
0
2
G0c
p ps (1) сI 0 Z (1) e p pr
G0
E
Z (0) 0 I 0 0 1
p ps (0) с p pr (0) с 1 p pr
Случай, когда pps (1) pps (0) :
1 p pr
2
G0c
2
E
сI 0 Z (1) e p pr с 1 p pr ln I 0 Z (1) c ln
p pr
G0
G0
G0
E
h

4.

Оптимальное обнаружение сигнала
(сигнал с неизвестной начальной фазой)
Алгоритм оптимального обнаружения
1 p pr
Ec
порог h
ln
G0
p pr
2
ln I 0 Z h
G0
c2
Z Z Z
T
Z y (t )U (t )cos 0t (t ) dt
c
0
s2
T
Z s y (t )U (t )sin 0t (t ) dt
0

5.

Оптимальный корреляционный обнаружитель
(сигнал с неизвестной начальной фазой)
ZC
T
0
y (t )
сигнал
2
ln I 0 Z h
есть
G0
2
Z2
Z
2
ln I 0 Z
G0
U (t )cos 0t (t )
ПУ
ZS
T
h
2
0
U (t )sin 0t (t )
Z
сигнала
2
ln I 0 Z h
нет
G0
Z h* сигнал есть
ПУ
Z h* сигнала нет
2
ln I 0 Z
G0
h*
h
Оптимальный порог
0
Z
h*
h
1 p pr
Ec
G
ln
, h* 0 I 0 1 e h
G0
p pr
2

6.

Характеристики оптимального обнаружителя
(сигнал с неизвестной начальной фазой)
Критерий Неймана-Пирсона:
Вероятность ложной тревоги
pобн max при заданной допустимой pЛТ
pЛТ P Z h* 0 w Z | 0 dZ
h*
2
2
2
Так как Z Z c Z s , то по аналогии с огибающей шума U U шc U шs
2
Z2
Z 2 2
w Z | 0 2 e
, Z 0 распределение Релея с параметром D Z C D Z S
Z c T
cos
y
(
t
)
U
(
t
)
s
0t (t ) dt
sin
Z 0
T
Дисперсия интеграла n(t ) s (t )dt не зависит от вида сигнала и равна
0
D Z C D Z S
G0
Eс
2
G0
Eс
2
G0
Eс
2

7.

Характеристики оптимального обнаружителя
(сигнал с неизвестной начальной фазой)
pЛТ
w( Z )
1
pЛТ
h*
Z
0
0
h*
Вероятность ложной тревоги
Порог
pЛТ
Z
* 2 e
h
h* 2ln pЛТ , где
Z2
2 2
G0
Eс
2
dZ e
h*2
2 2

8.

Характеристики оптимального обнаружителя
(сигнал с неизвестной начальной фазой)
Вероятность обнаружения
pобн w Z | 1 dZ
h*
По аналогии с огибающей суммы сигнала и шума
Z ZZ
w Z | 1 2 I 0 2с e
Z 2 Z с2
2 2
, Z 0 распределение Райса с параметрами Z с и .
Z с Z сc2 Z сs2 напряжение на входе ПУ при отсутствии шума; D Z C D Z S
G0
Eс
2
T
Z U (t )cos 0t (t ) U (t )cos 0t (t ) dt
c
с
0
T
T
1
1
U 2 (t )cos dt U 2 (t )cos 2 0t 2 (t ) dt Eс cos
20
20
Eс cos
T
Eс при T 1
2 f0
Z U (t )cos 0t (t ) U (t )sin 0t (t ) dt Eс sin
s
с
0
2
2
Z с Z сc Z сs
Eс cos
Eс
2
Eс sin
2

9.

Характеристики оптимального обнаружителя
(сигнал с неизвестной начальной фазой)
Z
x
Z 2 Z с2
ZZ
Z
Z
2
w Z | 1 dZ 2 I 0 2с e 2 dZ xс с
h*
h*
h*
xh*
Вероятность обнаружения
pобн
xI xx e
0
с
x 2 xс2
2
dx Q xс , xh*
x*
h
Q , xI 0 x e
x
2
2
2
dx Q-функция Маркума
pобн
Z с h*
Q ,
2 Eс
Q
, 2ln pЛТ
G0
Zс
Eс
G0
Eс
2
2 Eс
G0
h*
2ln pЛТ

10.

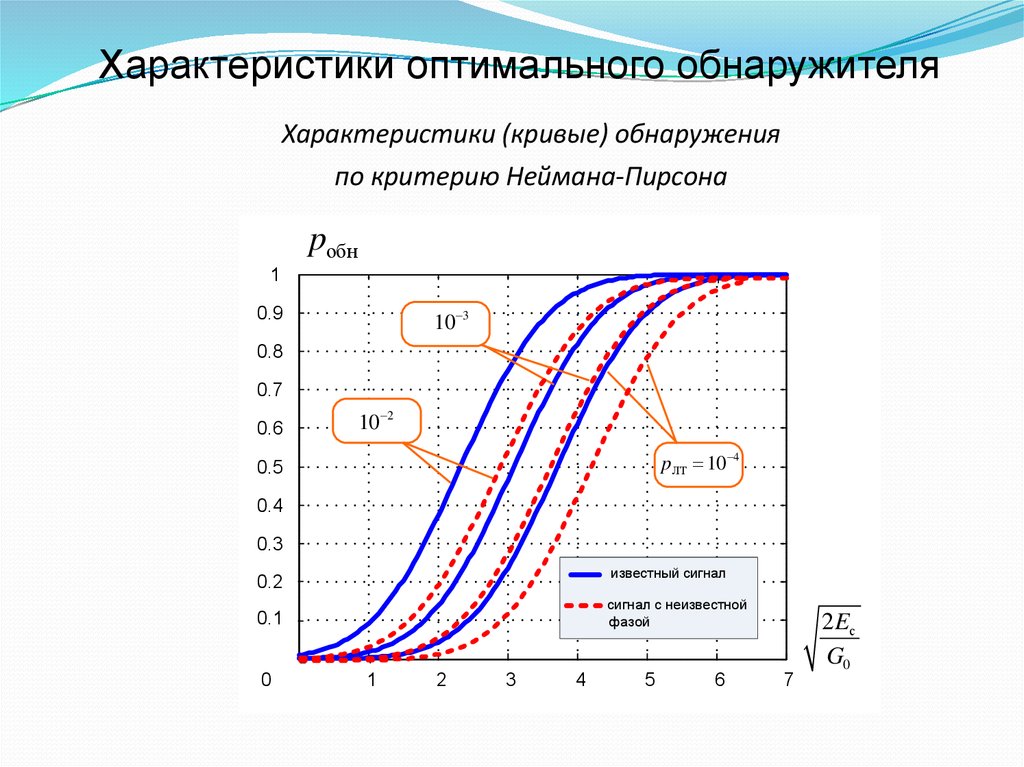
Характеристики оптимального обнаружителя
Характеристики (кривые) обнаружения
по критерию Неймана-Пирсона
pобн
1
0.9
10 3
0.8
0.7
0.6
10 2
pЛТ 10 4
0.5
0.4
0.3
известный сигнал
0.2
сигнал с неизвестной
фазой
0.1
0
1
2
3
4
5
6
2Eс
G0
7

11.

Оптимальное различение
полностью известных сигналов
y (t ) s (t ) n(t )
Принятая смесь сигнала и шума
1, если сигнал s1 (t )
0, если сигнал s2 (t )
s (t ) s1 (t ) 1 s2 (t )
различение
оценка
сигналов
параметра
Апостериорная вероятность параметра
p ps ( ) сeq( ) e
Ec ( )
G0
p pr ( )
T
2
q ( )
y (t ) s (t )dt корреляционный интеграл
G0 0
T
Eс ( ) s 2 (t )dt энергия сигнала
0

12.

Оптимальное различение двух
полностью известных сигналов
1
0
s (t ) s1 (t )
T
def
2
q(1)
y (t ) s1 (t )dt q1
G0 0
T
def
Eс (1) s (t )dt Eс1
2
1
0
p ps (1) сe q1 e
p ps1
s (t ) s2 (t )
T
def
2
q(0)
y (t ) s2 (t )dt q2
G0 0
T
def
Eс (0) s (t )dt Eс2
2
2
0
Ec1
G0
p pr (1)
p pr1
p ps (0) сeq2 e
pps 2
Ec2
G0
p pr (0)
ppr 2

13.

Оптимальное различение двух
полностью известных сигналов
Оценка параметра
1 (сигнал s1 (t )), если p ps1 p ps 2
ˆ
0 (сигнал s2 (t )), если p ps1 p ps 2
Случай, когда pps1 pps 2 :
сe q1 e
Ec1
G0
p pr1 сe q2 e
Ec2
G0
p pr 2
e q1 q2
p pr 2
p pr1
e
Ec1 Ec2
G0
E Ec2
q1 q2 ln
c1
p pr1
G0
q
порог h
p pr 2
Алгоритм оптимального различения
T
T
2
2
q q1 q2
y (t ) s1 (t )dt
y (t ) s2 (t )dt h
G0 0
G0 0

14.

Оптимальный приёмник различения
двух известных сигналов
2
G0
T
q1
0
q
y (t )
s1 (t )
ПУ
-
2
G0
T
q h сигнал s1 (t )
q2
h
0
s2 (t )
Оптимальный порог
h ln
p pr 2
p pr1
Ec1 Ec2
G0
q h сигнал s2 (t )

15.

16.

Вероятность ошибки при оптимальном
различении двух известных сигналов
Статистические характеристики напряжения на входе ПУ
T
T
2
2
q q1 q2
y (t ) s1 (t ) s2 (t ) dt
y (t ) s (t )dt qс qш
G0 0
G0 0
s (t )
T
2
s1 (t ) s (t )dt , если действует s1 (t )
qс | s1
G0 0
Математическое
q qс
T
ожидание
2
q | s
s (t ) s (t )dt , если действует s2 (t )
с 2 G 2
0 0
Дисперсия D q 2 q 2 qш qш
2
T
2
Шумовая составляющая qш
n(t ) s(t ) dt
2 E s
2
G0 0
q
G0
не зависит от того, какой сигнал действует

17.

Вероятность ошибки при оптимальном
различении двух известных сигналов
Условные плотности вероятности
2
q ( qс | s1 )
1
w q | s1
exp
2
2 q
q 2
2
q ( qс | s2 )
1
w q | s2
exp
2
2 q
q 2
Условное математическое ожидание
T
T
2
2
q
|
s
s
(
t
)
s
(
t
)
dt
q
|
s
s2 (t ) s (t )dt
с 1
с 2
1
G0 0
G0 0
T
2
E
Дисперсия 2 q s , где E s s(t ) 2 dt
G0
0

18.

Вероятность ошибки при оптимальном
различении двух известных сигналов
T
T
T
T
T
0
0
0
E s s (t ) 2 dt s1 (t ) s2 (t ) dt s1 (t ) 2 dt 2 s1 (t ) s2 (t )dt s2 (t ) 2 dt
2
0
0
Eс1 Eс
T
1
2 Eс 1 s1 (t ) s2 (t )dt 2 Eс 1 r12
Eс 0
r12 коэфф.взаимной
корреляции сигналов
Eс2 Eс
4 Eс 1 r12
G0
2
q
T
T
2 Eс 1 r12
2
2
q
|
s
s
(
t
)
s
(
t
)
dt
s
(
t
)
s
(
t
)
s
(
t
)
dt
с 1
1
1
1
2
G0 0
G0 0
G0
T
T
2 Eс r12 1
2
2
qс | s1
qс | s2 s2 (t ) s(t )dt s2 (t ) s1 (t ) s2 (t ) dt
G0 0
G0 0
G0

19.

Вероятность ошибки при оптимальном
различении двух известных сигналов
Условные плотности вероятности и условные вероятности ошибок
w q | s1
w q | s2
q
qс | s2
p s2 | s1
p s1 | s2
w q | s d q
2
h 0
qс | s1
p s1 | s2
p s2 | s1
h 0
p s2 | s1 p s1 | s2
h 0
w q | s d q
1

20.

Вероятность ошибки при оптимальном
различении двух известных сигналов
2E
с
1 r12
0
0 qс | s1
G0
p s2 | s1 w q | s1 d q
4 E 1 r
q
с
12
G
0
Eс
Eс
1
1 r12
1 r12 p s1 | s2
G0
т.к. ( x ) 1 ( x )
G0
Вероятность ошибки различения
pош
Eс
1
p s2 | s1 p s1 | s2 p s2 | s1 1
1 r12
2
G0

21.

Вероятность ошибки при оптимальном
различении двух известных сигналов
Противоположные сигналы:
r12 1
Ортогональные сигналы:
r12 0
Неразличимые сигналы:
r12 1
pош. пр
"Двоичное" отношение сигнал-шум qдв
2 Eс
1
G0
pош. орт
pош min
Eс
1
G
0
pош
1
pош max
2
Eс
E
, qдв дБ 10lg с
G0
G0

22.

Вероятность ошибки при оптимальном
различении двух известных сигналов
pош
Ортогональные сигналы
10
10
10
10
10
10
-1
-2
-3
3 дБ
Противоположные сигналы
-4
-5
qдв дБ
-6
0
1
2
3
4
5
6
7
8
9
10

23.

Оптимальный приёмник для различения
M равновероятных сигналов с одинаковой
энергией
y (t )
R1
T
1-й
канал
0
argmax
s1 t
T
M-й
канал
mˆ
RM
0
sM t
sˆ t smˆ t
T
Rm y (t ) sm (t ) dt
0

English Русский Rules