Similar presentations:
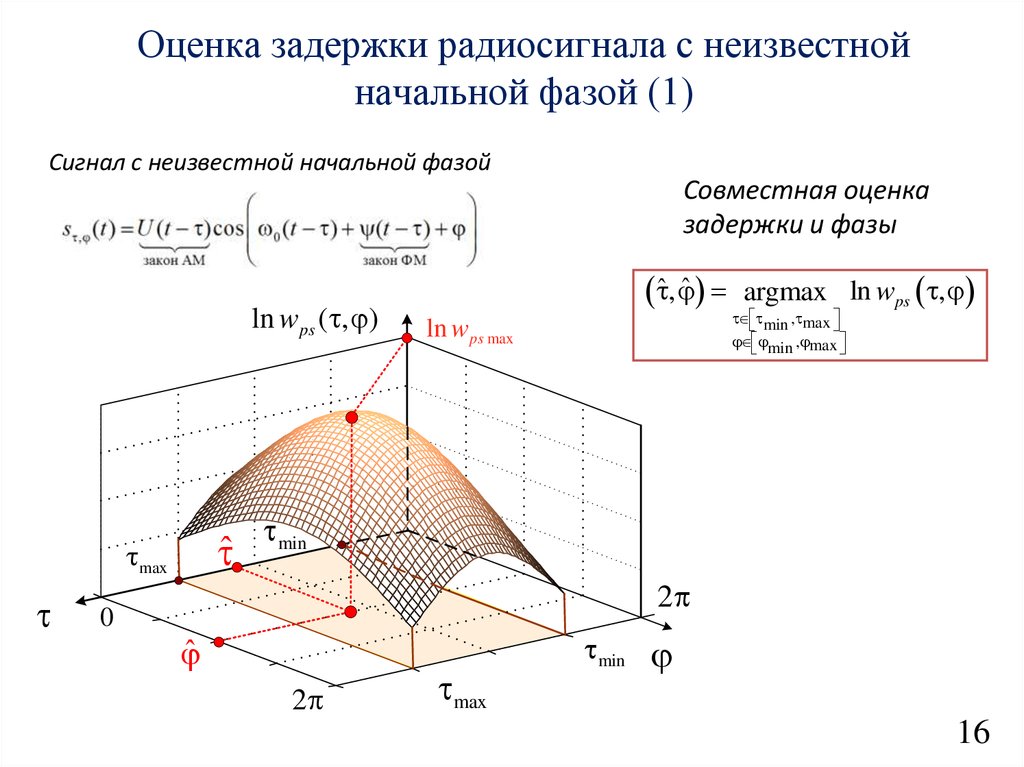
Оценка задержки радиосигнала с неизвестной начальной фазой
1.
Оценка задержки радиосигнала с неизвестнойначальной фазой (1)
Сигнал с неизвестной начальной фазой
Совместная оценка
задержки и фазы
ln wps ( , )
ˆ
max
ˆ , ˆ
ln wps max
argmax ln wps ,
min , max
min , max
min
2
0
ˆ
2
max
min
16
2.
Оценка задержки радиосигнала с неизвестнойначальной фазой (2)
Усреднение по случайной начальной фазе
Апостериорная плотность вероятности задержки w ps ( )
w
ps
( | )w pr ( )d
Априорная плотность вероятности фазы w pr ( )
1
, 0,2
2
Условная апостериорная плотность вероятности:
Апостериорная плотность вероятности задержки:
2
2
1
q ( , )
w ps ( ) w ps ( | ) w pr ( ) d c
e
d w pr ( )
2 0
0
17
3.
Оценка задержки радиосигнала с неизвестнойначальной фазой (3)
4.
Оценка задержки радиосигнала с неизвестнойначальной фазой (4)
Корреляционный интеграл
q( , )
2
2
Z c ( )cos 0 Z s ( )sin 0
Z ( )cos ( ) 0
G0
G0
Z ( ) Z c ( ) 2 Z s ( ) 2 , Z c ( ) Z ( )cos ( ), Z s ( ) Z ( )sin ( )
Апостериорная плотность вероятности задержки
2
wps ( ) c I 0 Z ( ) wpr ( )
G0
19
5.
Оценка задержки радиосигнала с неизвестнойначальной фазой (5)
Логарифм апостериорной плотности вероятности задержки
2
ln wps ( ) ln c ln I 0 Z ( ) ln wpr ( )
G0
ln I 0 ( x)
При равномерном априорном
ln I 0 x − монотонно
распределении задержки
2
ln wps ( ) const ln I 0 Z ( )
G0
возрастающая
x
0
функция
ˆ argmax ln wps ( ) argmax Z ( )
Оценка задержки:
min , max
min , max
argmax Z ( )2 argmax Z c ( ) 2 Z s ( ) 2
min , max
min , max
20
6.
Оценка задержки радиосигнала с неизвестнойначальной фазой (6)
Сигнал с задержкой 0 :
s 0 , (t ) U (t 0 ) cos 0 (t 0 ) (t 0 )
Алгоритм оценки задержки
T
Z c ( ) y (t )U (t ) cos 0t (t ) dt
0
T
Z ( ) y (t )U (t )sin 0t (t ) dt
s
0
Z ( ) Z c ( ) 2 Z s ( ) 2
ˆ argmax Z ( ) argmax Z c ( ) 2 Z s ( ) 2
min , max
min , max
21
7.
Оптимальный корреляционный приёмникрадиосигнала с неизвестной начальной фазой
Z C 1
y (t )
T
2
0
U (t 1 )cos 0t (t 1 )
T
Z 2 1
Z S 1
2
0
argmax
U (t 1 )sin 0t (t 1 )
Z C M
T
2
0
Z
U (t M )cos 0t (t M )
T
Z S M
2
M
ˆ
mˆ argmax Z 2 ( m )
m 1, M
ˆ mˆ
2
0
U (t M )sin 0t (t M )
22
8.
Максимальное отношение сигнал-шумна выходе коррелятора при измерении задержки
Принимаемое колебание
y (t ) s(t 0 ) n(t )
Корреляционный интеграл
2
q( )
y (t ) s(t )dt qс ( ) qш ( )
G0 0
T
T
2
qс ( )
s(t 0 ) s(t )dt
G0 0
T
2
qш ( )
n(t ) s(t )dt
G0 0
- сигнальная функция
- шумовая функция
Максимальное отношение сигнал-шум по напряжению:
max
qс max
qш
23
9.
Вычислениеqс max
Сигнальная функция как скалярное произведение векторов:
T
2
2
qс ( )
s
(
t
)
s
(
t
)
dt
s 0 , s
0
G0 0
G0
s s , s s (t )dt Eс
0
T
2
s 0 s 0 , s 0 s (t 0 )dt Eс
0
T
2
s
0
s s 0
, s max при s s 0 , т.е. при s(t ) s (t 0 )
T
qс max
2 Eс
2
2
qс ( 0 )
s(t 0 ) dt
G0 0
G0
24
10.
Вычисление qш
Дисперсия шумовой функции:
25
11.
3.2. Оптимальное обнаружение сигнала(полностью известный сигнал)
Принятая смесь сигнала и шума
1, если сигнал есть
0, если сигнала нет
y (t ) s(t ) n(t ) s (t ) n(t )
обнаружение
оценка
сигнала
параметра
Апостериорная вероятность параметра
p ps ( ) сeq( ) e
T
Ec ( )
G0
p pr ( )
T
2
2
q ( )
y
(
t
)
s
(
t
)
dt
y (t ) s(t )dt корреляционный интеграл
G0 0
G0 0
T
T
Eс ( ) s (t )dt 2 s 2 (t )dt энергия сигнала
2
0
0
26
12.
Оптимальное обнаружение сигнала(полностью известный сигнал - 1)
1
0
s (t ) s (t ) s (t )
s (t ) s(t ) 0
T
def
2
q(1)
y (t ) s(t )dt q
G0 0
T
def
Eс (1) s (t )dt Eс
2
q(0) 0
Eс (0) 0
0
p ps (1) сeq e
Ec
G0
p pr (1)
p ps (0) с p pr (0)
27
13.
Оптимальное обнаружение сигнала(полностью известный сигнал - 2)
Оценка параметра
1 (сигнал есть), если p ps (1) p ps (0)
ˆ
0 (сигнала нет), если p ps (1) p ps (0)
Случай, когда p ps (1) p ps (0)
сe e
q
Ec
G0
p pr (1) с p pr (0) e
q
def
p pr (1) p pr
p pr (0)
p pr (1)
e
Ec
G0
q ln
p pr (0)
p pr (1)
Ec
G0
p pr (0) 1 p pr
Алгоритм оптимального обнаружения
T
1 p pr Ec
2
q
y (t ) s(t )dt ln
G0 0
p pr
G0
порог h
28
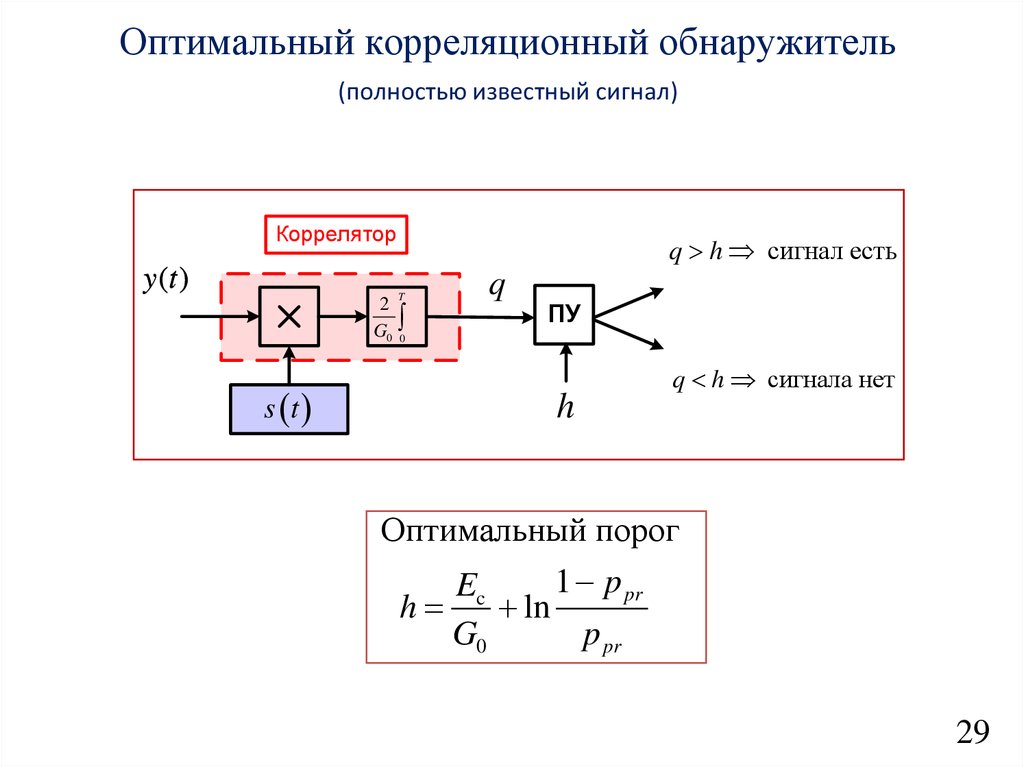
14.
Оптимальный корреляционный обнаружитель(полностью известный сигнал)
Коррелятор
y (t )
2
G0
s t
q h сигнал есть
T
q
ПУ
0
q h сигнала нет
h
Оптимальный порог
1 p pr
Ec
h
ln
G0
p pr
29
15.
Характеристики оптимального обнаружителя(полностью известный сигнал - 1)
Возможные ситуации при обнаружении
ˆ
1
1
0
правильное
обнаружение
ложное срабатывание
[ложная тревога (ЛТ)]
pобн
0
пропуск
сигнала
pпроп
pпроп pобн 1
pЛТ
правильное
необнаружение
pнеобн pЛТ 1
pнеобн
Независимые вероятности:
30
16.
Характеристики оптимального обнаружителя(полностью известный сигнал - 2)
Статистические характеристики корреляционного интеграла
T
T
2
2
Корреляционный интеграл q ( )
y
(
t
)
s
(
t
)
dt
s(t ) n(t ) s(t )dt
G0 0
G0 0
T
T
2
2
2 Eс
s 2 (t )dt
n
(
t
)
s
(
t
)
dt
qш
G0 0
G0 0
G0
2 Eс
мат.
ожидание
q
(
)
q
|
G0
2E
2 Eс
D qш с
2
дисперсия
D
q
(
)
G0
q
G0
qш 0
Условная плотность вероятности
корреляционного интеграла
(нормальное распределение):
w q |
1
q 2
2
q ( q | )
e
2 2q
31
17.
Характеристики оптимального обнаружителя(полностью известный сигнал - 3)
q | 1
w q | 1
w q | 0
pобн
0
h
q
pЛТ
32
18.
Характеристики оптимального обнаружителя(полностью известный сигнал - 4)
Вероятность ложной тревоги
Вероятность обнаружения
pЛТ w q | 0 dq
pобн w q | 1 dq 1
h
h
h
1
w q | 0 dq
h
1
h
1
1
q
h
1
q
pЛТ
2
e
2
q
2 2q
dq
1 h
h
1
q
2 Eс
G0
1
q
2
q ( q | 1) 2
e
2 Eс
h
G0
1
2 Eс
G0
2 2q
h
w q | 1 dq
h (q | 1)
dq 1
q
1 h 2 Eс
2 Eс
G0
G0
h
2 Eс
1
G0
q
pобн
33
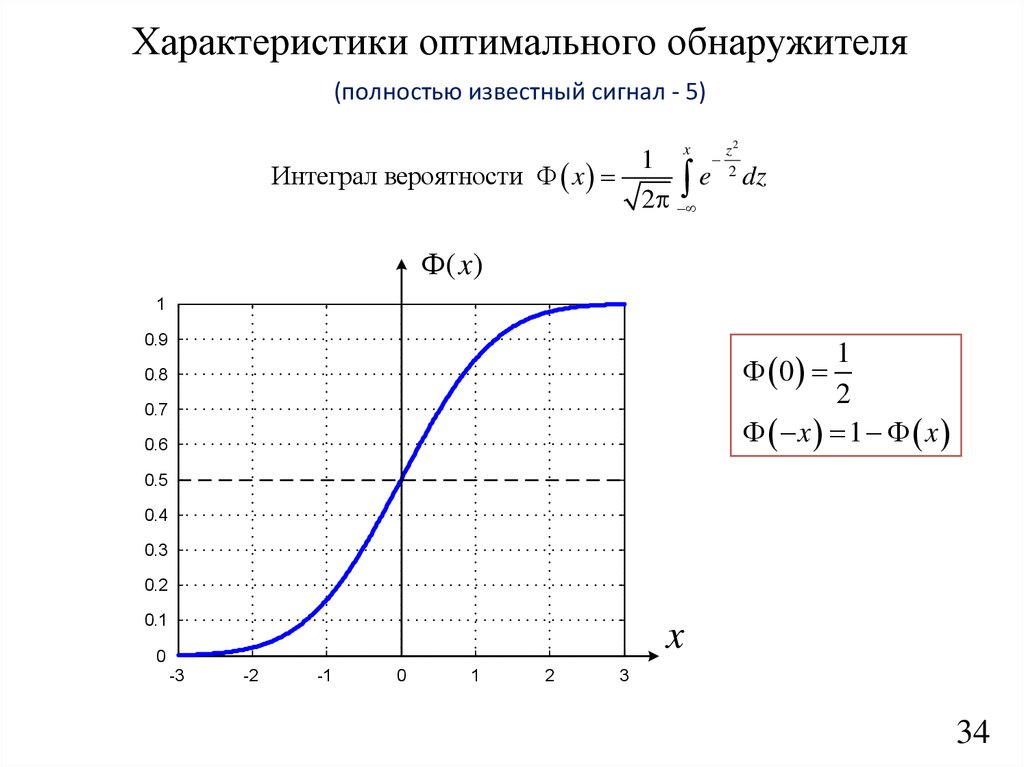
19.
Характеристики оптимального обнаружителя(полностью известный сигнал - 5)
x
2
z
1
Интеграл вероятности x
e 2 dz
2
( x)
1
0.9
1
2
x 1 x
0
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
x
0
-3
-2
-1
0
1
2
3
34
20.
Характеристики оптимального обнаружителя(полностью известный сигнал - 6)
Обнаружение по критерию максимума апостериорной вероятности
Полная вероятность ошибки
при оптимальном пороге
pош pпроп p pr pЛТ 1 p pr min
h ln
1 p pr
p pr
Ec
G0
Обнаружение по критерию Неймана-Пирсона
pобн max при заданной допустимой pЛТ
pобн
pЛТ
h
2 Eс
1
G0
q
h
1
q
pобн
2 Eс
h
G0 q
h
1 1 pЛТ
q
- нормированный порог
2 Eс
1
1 pЛТ
G0
35
21.
Характеристики оптимального обнаружителя:(полностью известный сигнал - 7)
Характеристики (кривые) обнаружения
по критерию Неймана-Пирсона
pобн
1
0.9
10 3
0.8
0.7
0.6
10 2
pЛТ 10 4
0.5
0.4
0.3
0.2
0.1
0
2Eс
G0
1
2
3
4
5
6
7
36
22.
Оптимальное обнаружение сигнала(сигнал с неизвестной начальной фазой - 1)
Апостериорная вероятность параметра
1
p ps ( ) p ps ( | )w pr ( )d
2
0
2
0
1 2 q ( , )
p ps ( | )d
сe
d e
2 0
T
Ec ( )
G0
p pr ( )
T
2
2
q( , )
y
(
t
)
s
(
t
)
dt
y (t ) U (t )cos 0 (t ) dt
,
G0 0
G0 0
2
2
1
q ( , )
e
d
I
Z
(
)
0
2 0
G
0
T
Z c ( ) y (t ) U (t )cos 0t (t ) dt
0
Z ( ) Z c ( ) 2 Z s ( ) 2
T
Z s ( ) y (t ) U (t )sin 0t (t ) dt
0
37
23.
Оптимальное обнаружение сигнала(сигнал с неизвестной начальной фазой - 2)
2
p ps ( ) сI 0 Z ( ) e
G0
1
Ec ( )
G0
p pr ( )
0
2
G0c
p ps (1) сI 0 Z (1) e p pr
G0
E
Z (0) 0 I 0 0 1
p ps (0) с p pr (0) с 1 p pr
Случай, когда pps (1) pps (0) :
1 p pr
2
G0c
2
Ec
сI 0 Z (1) e p pr с 1 p pr ln I 0 Z (1)
ln
p pr
G0
G0
G0
E
h
38
24.
Оптимальное обнаружение сигнала:(сигнал с неизвестной начальной фазой - 3)
Алгоритм оптимального обнаружения
1 p pr
Ec
порог h
ln
G0
p pr
2
ln I 0 Z h
G0
c2
Z Z Z
T
Z c y (t )U (t )cos 0t (t ) dt
0
s2
T
Z s y (t )U (t )sin 0t (t ) dt
0
39
25.
Оптимальный корреляционный обнаружитель(сигнал с неизвестной начальной фазой)
ZC
T
0
y (t )
сигнал
2
ln I 0 Z h
есть
G0
2
Z2
Z
2
ln I 0 Z
G0
U (t )cos 0t (t )
ПУ
ZS
T
h
2
0
U (t )sin 0t (t )
Z
сигнала
2
ln I 0 Z h
нет
G0
Z h* сигнал есть
ПУ
Z h* сигнала нет
2
ln I 0 Z
G0
h*
h
Оптимальный порог
0
Z
h
*
h
1 p pr
Ec
G
ln
, h* 0 I 0 1 e h
G0
p pr
2
40
26.
Характеристики оптимального обнаружителяХарактеристики (кривые) обнаружения
по критерию Неймана-Пирсона
pобн
1
0.9
10 3
0.8
0.7
0.6
10 2
pЛТ 10 4
0.5
0.4
0.3
известный сигнал
0.2
сигнал с неизвестной
фазой
0.1
0
1
2
3
4
5
6
2Eс
G0
7
41
27.
3.3. Оптимальное различениеполностью известных сигналов
y (t ) s (t ) n(t )
Принятая смесь сигнала и шума
s (t ) s1 (t ) 1 s2 (t )
1, если сигнал s1 (t )
0, если сигнал s2 (t )
различение
оценка
сигналов
параметра
Апостериорная вероятность параметра
p ps ( ) сeq( ) e
Ec ( )
G0
p pr ( )
T
2
q ( )
y (t ) s (t )dt корреляционный интеграл
G0 0
T
Eс ( ) s 2 (t )dt энергия сигнала
0
42
28.
Оптимальное различение двухполностью известных сигналов (1)
43
29.
Оптимальное различение двухполностью известных сигналов (2)
44
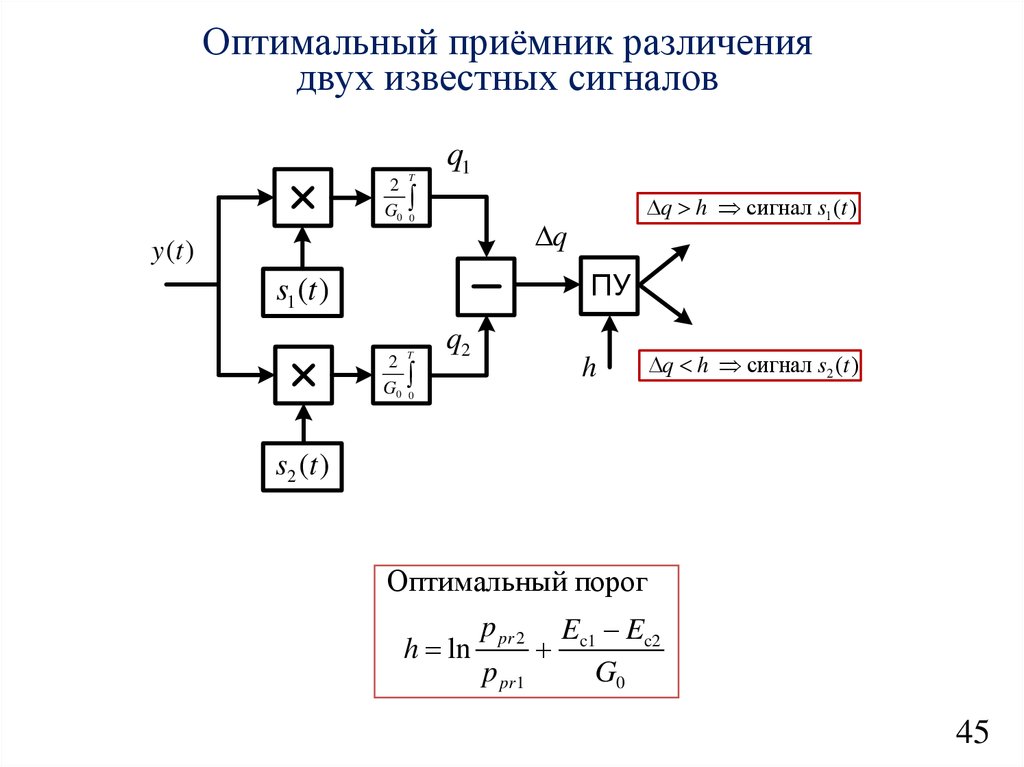
30.
Оптимальный приёмник различениядвух известных сигналов
2
G0
T
q1
0
q
y (t )
s1 (t )
ПУ
-
2
G0
T
q h сигнал s1 (t )
q2
h
q h сигнал s2 (t )
0
s2 (t )
Оптимальный порог
h ln
p pr 2
p pr1
Ec1 Ec2
G0
45
31.
Вероятность ошибки при оптимальном различениидвух известных сигналов (1)
1
p
p
pr1
pr 2
2
Eс1 Eс2 Eс
Равновероятные сигналы
с одинаковой энергией
h 0
Вероятность ошибки различения
1
pош p s2 | s1 p pr1 p s1 | s2 p pr 2 p s2 | s1 p s1 | s2
2
условные вероятности ошибок
при приёме сигналов
p s1 | s2 P q h | s2
w q | s d q
2
h 0
p s2 | s1 P q h | s1
h 0
w q | s d q
1
46
32.
Вероятность ошибки при оптимальном различениидвух известных сигналов (2)
Статистические характеристики напряжения на входе ПУ
33.
Вероятность ошибки при оптимальном различениидвух известных сигналов (3)
Условные плотности вероятности
2
q ( qс | s1 )
1
w q | s1
exp
2
2 q
q 2
2
q
(
q
|
s
)
1
с
2
w q | s2
exp
2
2
q 2
q
Условное математическое ожидание
T
T
2
2
q
|
s
s
(
t
)
s
(
t
)
dt
q
|
s
s2 (t ) s(t )dt
с 1
с 2
1
G0 0
G0 0
T
2
E
Дисперсия 2 q s , где E s s(t ) 2 dt
G0
0
48
34.
Вероятность ошибки при оптимальном различениидвух известных сигналов (4)
49
35.
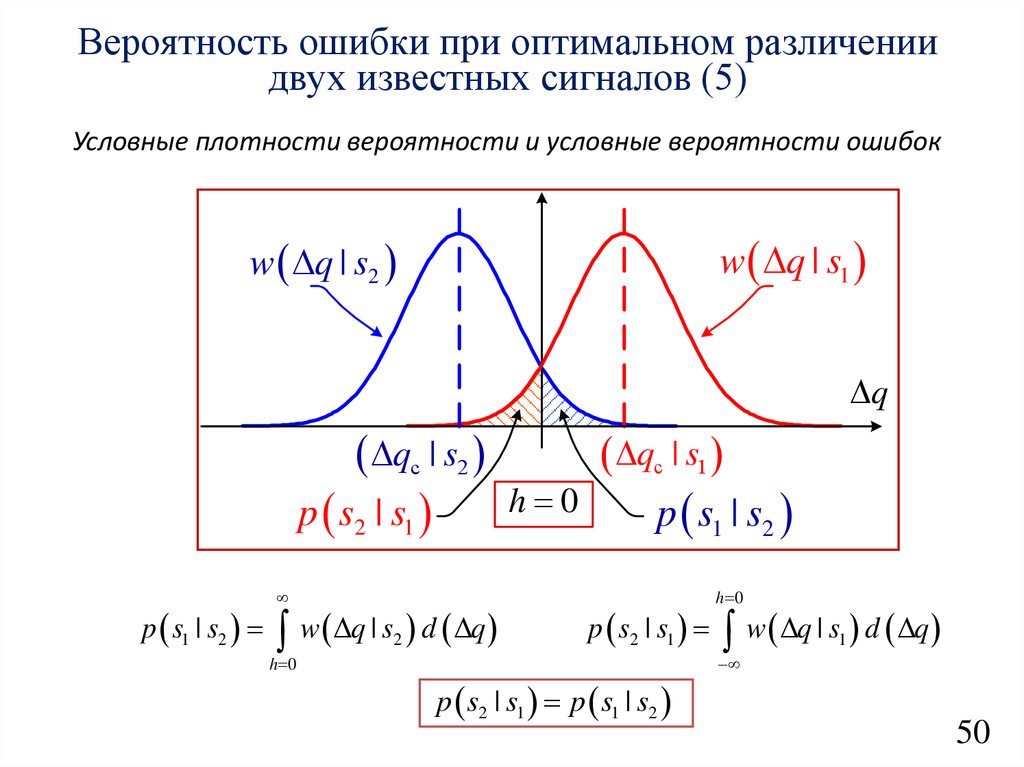
Вероятность ошибки при оптимальном различениидвух известных сигналов (5)
Условные плотности вероятности и условные вероятности ошибок
w q | s1
w q | s2
q
qс | s2
p s2 | s1
p s1 | s2
w q | s d q
2
h 0
qс | s1
p s1 | s2
p s2 | s1
h 0
p s2 | s1 p s1 | s2
h 0
w q | s d q
1
50
36.
Вероятность ошибки при оптимальном различениидвух известных сигналов (6)
2E
с
1 r12
0
0 qс | s1
G0
p s2 | s1 w q | s1 d q
4 E 1 r
q
с
12
G
0
Eс
Eс
1
1 r12 p s1 | s2
1 r12
G0
т.к. ( x ) 1 ( x )
G0
Вероятность ошибки различения
pош
Eс
1
p s2 | s1 p s1 | s2 p s2 | s1 1
1 r12
2
G0
51
37.
Вероятность ошибки при оптимальном различениидвух известных сигналов (7)
Противоположные сигналы:
Ортогональные сигналы:
Неразличимые сигналы:
r12 1
2 Eс
pош. пр 1
G0
r12 0
r12 1
"Двоичное" отношение сигнал-шум qдв
pош. орт
pош min
Eс
1
G0
1
pош pош max
2
Eс
E
, qдв дБ 10lg с
G0
G0
52
38.
Вероятность ошибки при оптимальном различениидвух известных сигналов (8)
pош
Ортогональные сигналы
10
10
10
10
10
10
-1
-2
-3
3 дБ
Противоположные сигналы
-4
-5
qдв дБ
-6
0
1
2
3
4
5
6
7
8
9
10
53
39.
Оптимальный приёмник различения Mравновероятных сигналов с одинаковой энергией
y (t )
R1
T
1-й
канал
0
argmax
s1 t
T
M-й
канал
mˆ
RM
0
sM t
sˆ t smˆ t
T
Rm y (t ) sm (t ) dt
0
54
40.
3.4. Оптимальная обработка сигналов сиспользованием согласованных фильтров
g СФ (t )
Импульсная характеристика
s ( t )
s (t )
g CФ (t ) cs (t0 t )
и
0
и
t
0
t0 и
t
Передаточная функция
t t x
0
K =СФ ( j ) F g СФ (t ) cs(t0 t )e j t dt t t0 x c s ( x )e j ( t0 x )d ( x )
dt dx
c s( x )e j t0 e j x dx ce j t0
АЧХ
K =СФ ( ) K =СФ ( j ) cS ( )
s ( x )e j x dx cS * ( j )e j t0
ФЧХ
=СФ ( ) arg K =СФ ( j ) ( ) t0
55
41.
Характеристики согласованного фильтра (1)Отклик СФ
y( ) g
yвых (t ) y (t ) gСФ (t )
СФ
(t ) d c y ( ) s( t0 t )d
cs (t0 (t ))
yвых (t0 ) c y ( ) s( )d
Корреляционный интеграл
2
q ( )
G0
T
y(t )s (t )dt
0
Отклик СФ на сигнал
sвых (t ) s(t ) g СФ (t )
s( ) g
cEс
СФ
(t ) d c s ( )s (t t0 ) d c Rс (t t0 )
cs t0 (t )
Пиковое значение отклика
s (t )
АКФ сигнала,
сдвинутая на t0
sвых max sвых (t0 ) cRs (0) c s 2 ( )d cEс
sвых (t )
Uс
Eс U с2 и
0
и
t
0
и
t
2 и
56
42.
Характеристики согласованного фильтра (2)Отношение сигнал-шум на выходе СФ
2
Дисперсия шума ш.
вых
G0
по теореме 2
Парсеваля
sвых.max
ш.вых
sвых max cEс
G 1
2
2
Gш. вых ( f )df G0 K СФ
( f )df 0
K
( )d
СФ
2 2
0
0
G0
g
(
t
)
dt
2
2
СФ
СФ
2 2
2
c
s
t
t
dt
c
0
G0
Eс
2
ш.вых c
G0
Eс
2
Теорема Парсеваля:
2
1
если X ( j ) F x (t ) , то x (t )dt
X
(
j
)
d
2
2
СФ
2Eс
G0
Максимальное отношение сигнал-шум на выходе СФ не зависит от вида
сигнала и определяется только отношением его энергии к спектральной
плотности шума
57
43.
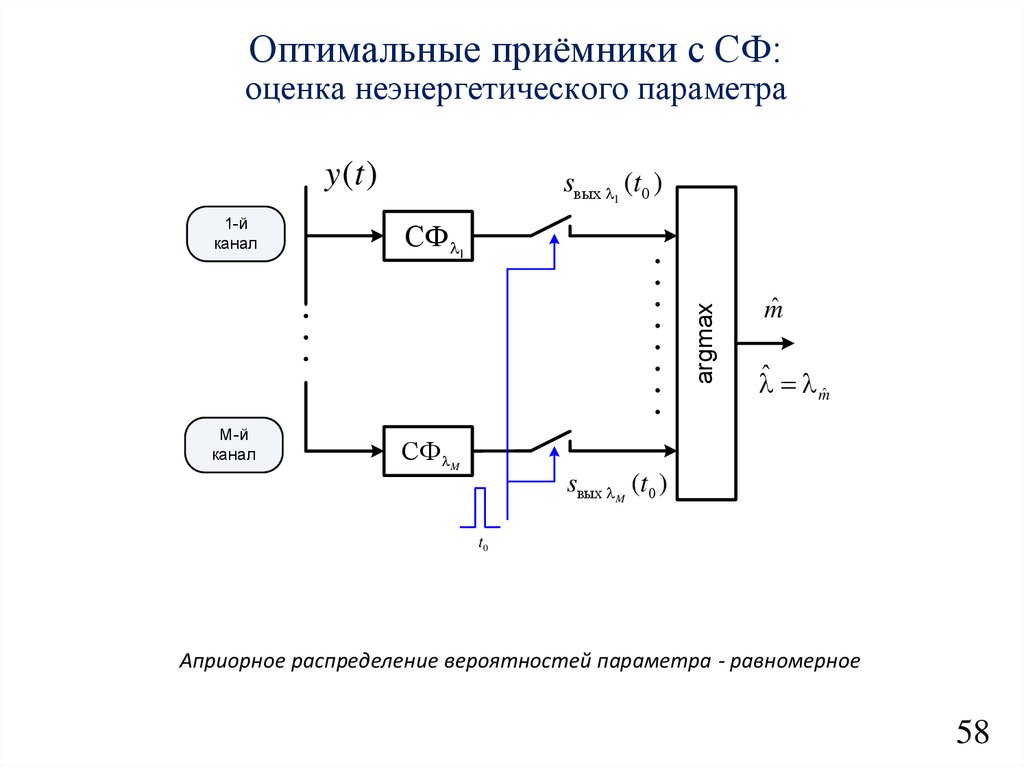
Оптимальные приёмники с СФ:оценка неэнергетического параметра
y (t )
СФ 1
argmax
1-й
канал
sвых 1 (t0 )
M-й
канал
mˆ
ˆ mˆ
СФ M
sвых M (t0 )
t0
Априорное распределение вероятностей параметра - равномерное
58
44.
Оптимальные приёмники с СФ:оценка задержки видеоимпульса
y (t )
t
yвых (t )
t
t1 t2 t3
tM
tmˆ
Априорное распределение вероятностей задержки - равномерное
y (t )
yвых (tm )
Сравнение
отсчётов
СФ
mˆ
mˆ arg max yвых (tm )
m 1, M
ˆ tmˆ и
t1 t2 t3 t4
59
45.
Оптимальные приёмники с СФ:оценка задержки радиоимпульса (1)
Влияние начальной фазы сигнала
0
2
s (t )
s (t )
t
t
и
gСФ (t )
gСФ (t )
t
и
sвых (t )
t
sвых (t )
t
t и
t
t и
60
46.
Оптимальные приёмники с СФ:оценка задержки радиоимпульса (2)
Сигнал со случайной начальной фазой
t
y (t )
СФ
(радио)
t
mˆ
Сравнение
отсчётов
АД
t1 t 2 t3 t 4
СФ
(видео)
2
t
y (t )
Сравнение
отсчётов
cos 0t
СФ
(видео)
mˆ
2
t1 t 2 t3 t 4
sin 0t
61
47.
Оптимальные приёмники с СФ:обнаружитель радиоимпульса
СФ
(видео)
2
t
y (t )
ПУ
cos 0t
СФ
(видео)
2
t0 и
h*
sin 0t
Согласованный фильтр для видеоимпульса
(СФ (видео))
+
и
-
62
48.
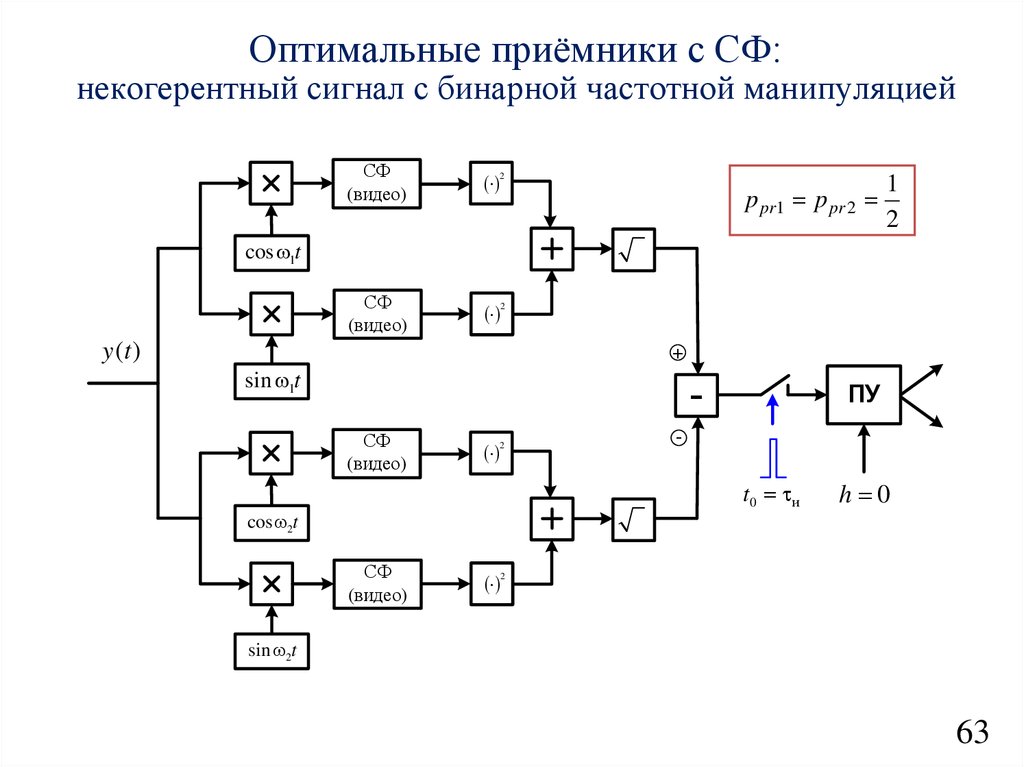
Оптимальные приёмники с СФ:некогерентный сигнал с бинарной частотной манипуляцией
СФ
(видео)
СФ
(видео)
2
p pr1 p pr 2
1
2
cos 1t
2
y (t )
+
sin 1t
СФ
(видео)
2
ПУ
-
t0 и
cos 2t
СФ
(видео)
h 0
2
sin 2t
63









































 physics
physics








