Similar presentations:
Расчет максимального отношения сигнал-шум на выходе оптимального приемника. Тема 4: Часть 3
1. Тема 4:
Часть 3:Расчет максимального отношения сигнал-шум на
выходе оптимального приемника.
Оптимальное обнаружение и различение сигналов.
2.
Максимальное отношение сигнал-шумна выходе коррелятора
Пример: корреляционный приемник для оценки задержки импульса
y (t ) s(t 0 ) n(t )
Принимаемое колебание
T
ˆ arg max R( ) arg max ( y(t ) s (t )dt ) arg max q( )
[ min , max ]
[ min , max ] 0
[ min , max ]
T
Корреляционный интеграл
2
q( )
y (t ) s(t )dt qс ( ) qш ( )
G0 0
T
2
qс ( )
s(t 0 ) s(t )dt
G0 0
T
2
qш ( )
n(t ) s(t )dt
G0 0
- сигнальная функция (регулярная)
- шумовая функция (случайная)
Максимальное отношение сигнал-шум по напряжению:
max
qс max
qш
3.
Вычисление максимума сигнальной функцииСигнальная функция как скалярное произведение векторов:
T
2
2
qс ( )
s
(
t
)
s
(
t
)
dt
s 0 , s
0
G0 0
G0
s s , s s (t )dt Eс
0
T
s 0 s 0 , s 0 s 2 (t 0 )dt Eс
0
T
2
s
0
s s 0
, s max при s s 0 , т.е. при s (t ) s (t 0 )
T
qс max
2 Eс
2
2
qс ( 0 )
s
(
t
)
dt
0
G0 0
G0
qс max
4.
qшВычисление СКО шумовой функции
T
Дисперсия шумовой функции:
2
qш ( )
n(t ) s(t )dt
G0 0
T
так как qш ( ) 0, то
2qш
2
G0
2
qш
2T T
n(t1 )n(t2 ) s (t1 ) s (t2 )dt1dt2
0 0
АКФ шума n(t1 )n(t2 ) K n (t2 t1 ) K n ( x)
2
qш
2
G0
T
2
2
q ( )
n
(
t
)
s
(
t
)
dt
n(t2 ) s (t2 )dt2
1
1
1
G0 0
G0 0
2
ш
G0
( x)
2
2T T
T
T
G0
2
0 0 2 (t2 t1 )s(t1 )s(t2 )dt1dt2 G0 0 s(t1 ) 0 (t2 t1 )s(t2 )dt2 dt1
T
2 Eс
2
2
s
(
t
)
dt
1
1
G0 0
G0
qш
2 Eс
G0
max
s(t1 )
qс max
2 Eс
qш
G0
5.
Оптимальное обнаружение сигнала(полностью известный сигнал)
Принятая смесь сигнала и шума
1, если сигнал есть
0, если сигнала нет
y (t ) s (t ) n(t ) s (t ) n(t )
обнаружение
оценка
сигнала
параметра
Апостериорная вероятность параметра
p ps ( ) сeq( ) e
T
Ec ( )
G0
p pr ( )
T
2
2
q ( )
y
(
t
)
s
(
t
)
dt
y (t ) s(t )dt корреляционный интеграл
G0 0
G0 0
T
T
0
0
Eс ( ) s 2 (t )dt 2 s 2 (t )dt энергия сигнала
6.
Оптимальное обнаружение сигнала(полностью известный сигнал)
1
0
s (t ) s (t ) s(t )
s (t ) s (t ) 0
T
def
2
q(1)
y (t ) s (t )dt q
G0 0
T
def
Eс (1) s (t )dt Eс
2
q(0) 0
Eс (0) 0
0
p ps (1) сe e
q
Ec
G0
p pr (1)
p ps (0) с p pr (0)
7.
Оптимальное обнаружение сигнала(полностью известный сигнал)
Оценка параметра
1 (сигнал есть), если p ps (1) p ps (0)
ˆ
0 (сигнала нет), если p ps (1) p ps (0)
Случай, когда p ps (1) p ps (0)
сe e
q
Ec
G0
p pr (1) с p pr (0) e
q
def
p pr (1) p pr
p pr (0)
p pr (1)
e
Ec
G0
q ln
p pr (0) 1 p pr
Алгоритм оптимального обнаружения
T
1 p pr Ec
2
q
y (t ) s(t )dt ln
G0 0
p pr
G0
порог h
p pr (0)
p pr (1)
Ec
G0
8.
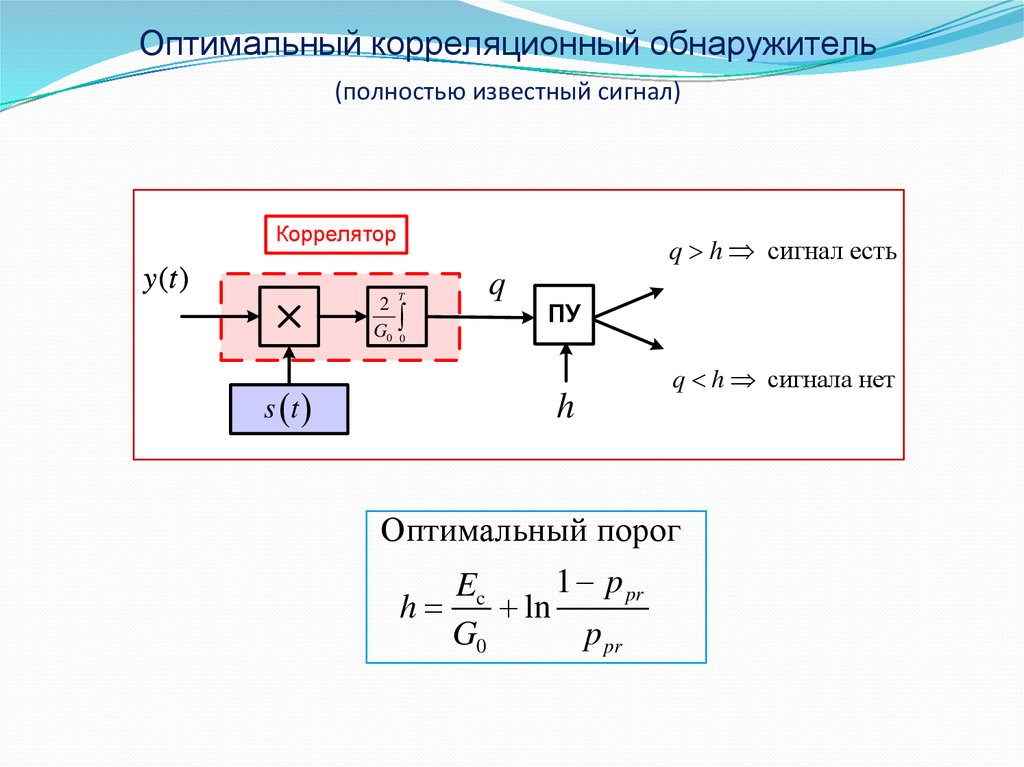
Оптимальный корреляционный обнаружитель(полностью известный сигнал)
Коррелятор
y (t )
2
G0
s t
q h сигнал есть
T
q
ПУ
0
q h сигнала нет
h
Оптимальный порог
1 p pr
Ec
h
ln
G0
p pr
9.
Характеристики оптимального обнаружителя(полностью известный сигнал)
Возможные ситуации при обнаружении
ˆ
1
1
0
правильное
обнаружение
ложное срабатывание
[ложная тревога (ЛТ)]
pобн
0
пропуск
сигнала
pпроп
pЛТ
правильное
необнаружение
pнеобн
pпроп pобн 1
pнеобн pЛТ 1
Независимые вероятности:
pобн P q h 1 D (Detection обнаружение)
pЛТ P q h 0 F (False Alarm ложная тревога)
10.
Характеристики оптимального обнаружителя(полностью известный сигнал)
Статистические характеристики корреляционного интеграла
T
T
2
2
Корреляционный интеграл q ( )
y
(
t
)
s
(
t
)
dt
s(t ) n(t ) s(t )dt
G0 0
G0 0
T
T
2
2
2 Eс
s 2 (t )dt
n
(
t
)
s
(
t
)
dt
qш
G0 0
G0 0
G0
2 Eс
мат.ожидание
q
(
)
q
|
G0
2E
2 Eс
D qш с
2
дисперсия
D
q
(
)
G0
q
G0
qш 0
Условная плотность
вероятности корреляционного
интеграла:
w q |
1
q 2
2
q ( q | )
e
2 2q
11.
Характеристики оптимального обнаружителя(полностью известный сигнал)
q | 1
w q | 1
w q | 0
pобн
0
Вероятность ложной тревоги
pЛТ P q h 0 w q | 0 dq
h
h
q
pЛТ
Вероятность обнаружения
pобн P q h 1 w q | 1 dq
h
12.
Характеристики оптимального обнаружителя(полностью известный сигнал)
Вероятность ложной тревоги
Вероятность обнаружения
pЛТ w q | 0 dq
pобн w q | 1 dq 1
h
h
h
1
w q | 0 dq
h
1
h
1
1
q
h
1
q
pЛТ
2
e
q2
2
2 q
dq
1 h
h
1
q
2 Eс
G0
1
q
2
q ( q | 1) 2
e
2 Eс
h
G0
1
2 Eс
G0
2 2q
h
w q | 1 dq
h (q | 1)
dq 1
q
1 h 2 Eс
2 Eс
G0
G0
h
2 Eс
1
G0
q
pобн
13.
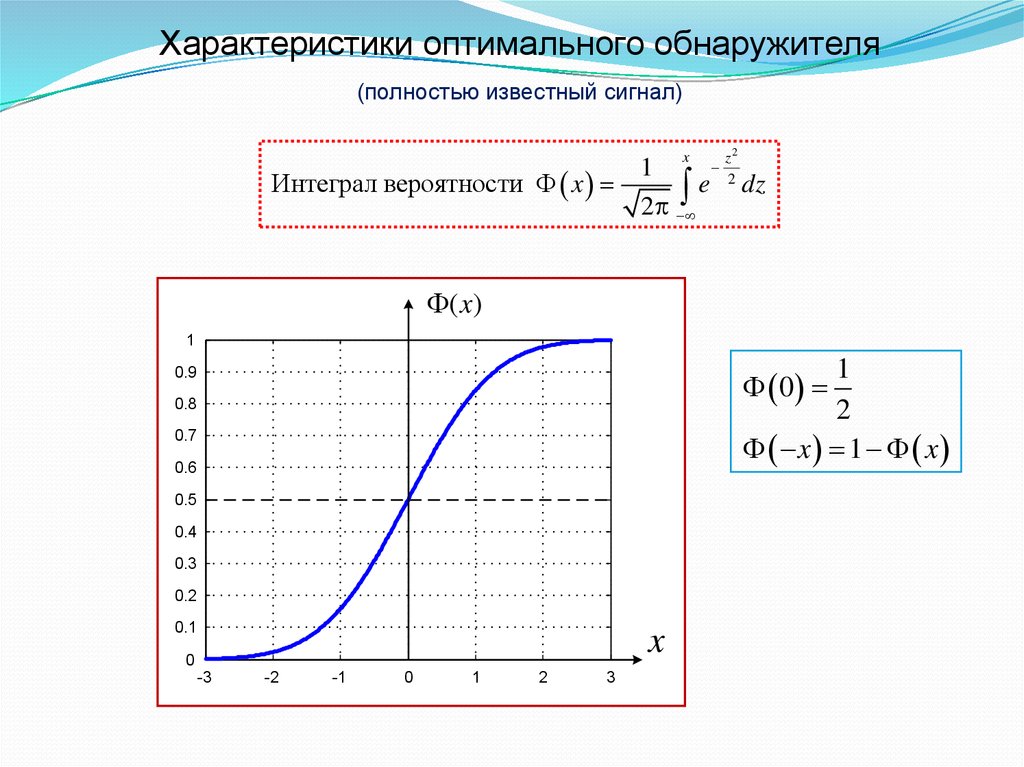
Характеристики оптимального обнаружителя(полностью известный сигнал)
Интеграл вероятности x
1
x
e
2
z2
2
dz
( x)
1
1
2
x 1 x
0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
x
0
-3
-2
-1
0
1
2
3
14.
Характеристики оптимального обнаружителя(полностью известный сигнал)
Обнаружение по критерию максимума апостериорной вероятности
Полная вероятность ошибки
при оптимальном пороге
pош pпроп p pr pЛТ 1 p pr min
h ln
1 p pr
p pr
Ec
G0
Обнаружение по критерию Неймана-Пирсона
pобн max при заданной допустимой pЛТ
pЛТ
h
2 Eс
2 Eс
h
pобн 1
G0
q
G0 q
h
h
1
1 1 pЛТ - нормированный порог
q
q
pобн
2 Eс
1
1 pЛТ
G0
15.
Характеристики оптимального обнаружителя(полностью известный сигнал)
Характеристики (кривые) обнаружения
по критерию Неймана-Пирсона
pобн
1
0.9
10 3
0.8
0.7
0.6
10 2
pЛТ 10 4
0.5
0.4
0.3
0.2
0.1
0
2Eс
G0
1
2
3
4
5
6
7













 physics
physics








