О некоторых задачах без начальных условий

1.

О некоторых задачах без начальныхусловий
Н.Р. Будцев
2023

2.

Введение
Задачи без начальных условий относятся к классу задач
описывающих установившиеся периодические или переходные
процессы, начавшиеся так давно, что начальные данные не
оказывают практически влияния на поведение решения в
момент наблюдения.
Такая независимость возможна лишь по истечении достаточного
времени. То есть, в таком случае можно говорить об
асимптотике решений по времени, стремящимся к
бесконечности. Поэтому такие асимптотики называются
«промежуточными», а соответствующие задачи без начальных
условий – «вырожденными».

3.

Введение
Например, для t ∈ ( − ∞ , ∞ ) единственным ограниченным
решением уравнения
du(t)
+ λu(t) = 1,
dt
λ > 0.
(1)
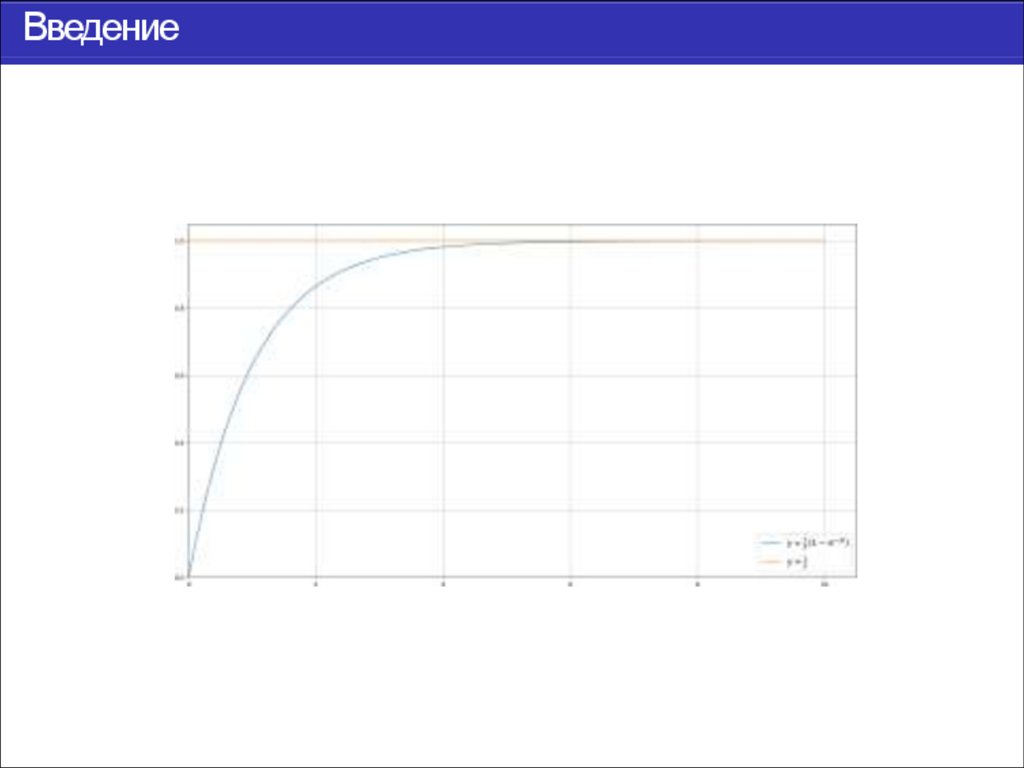
является u(t) = λ1 , а для t ∈ [0,∞ ) единственным решением
этого уравнения с условием
u(0) =0,
является функция
u 0 (t) =
1
(1 − e −λt ).
λ
Таким образом u(t) = 1 является
промежуточной
λ
асимптотикой функции u 0(t), то есть u 0(t) → u(t) при t → ∞ .
(2)

4.

Введение

5.

Постановка задачи
Определение и суть задач без начальных условий.
Обзор различных методов и подходов для решения задач
без начальных условий.
Исследование примеров задач без начальных условий.

6.

Уравнение свободных колебанийструны
Уравнение свободных колебаний струны —это уравнение,
которое описывает колебания струны в отсутствие внешних сил
или воздействий.
Уравнение свободных колебаний струны можно записать в виде
волнового уравнения:
2
∂2u
2∂ u
=a 2,
2
∂t
∂x
где u(x, t) - функция, представляющая поперечное смещение
струны в позиции x и в момент времени t, а a - скорость
распространения волны поструне.
(3)

7.

Уравнение свободных колебанийструны
Для полного описания колебаний струны с использованием
уравнения свободных колебаний (3) необходимо задать
начальные условия и краевые условия. Зададим следующие
начальные условия:
u(x, 0) = φ(x),
∂u(x,t)
∂t |t=0 = ψ(x)
(4)
и однородные граничные условия:
u(0, t) = 0,
u(l, t) = 0,
где l - длина струны. Это условие предполагает, что концы
струны закреплены и не могут двигаться.
(5)

8.

Уравнение свободных колебанийструны
Предполагая, что функции φ(x), ψ(x) из (4) разложимы в ряд
Фурье, решение уравнения (3) c начальными и граничными
условиями (4),(5) имеет вид:
Σ∞
u(x, t) =
(A n sin
n=1
где
A n = l2
Bn =
∫l
0
1
πna
πn
πn
πn
at + B ncos
at)sin
x,
l
l
l
(6)
φ(τ )sin( lπnτ )dτ,
∫l
0
(7)
ψ(τ )sin( πn
l τ )dτ.

9.

Уравнение свободных колебаний струны без начальных
условий
Чтобы перейти к задаче без начальных условий, рассмотрим
следующее уравнение:
2
∂2u
∂u
2∂ u
=
a
− α
,
2
2
∂t
∂x
∂t
где a > 0, 0 < x < l и t > − ∞ , с граничными условиями:
u(0, t)= 0,
u(l, t) = A cosωt.
u имеет смысл трения.
Слагаемое α ∂∂t
(8)
(9)

10.

Уравнение свободных колебаний струны без начальных
условий
Решение u(x, t) выглядят следующим образом:
u(x, t) = X 1 (x) cosωt − X 2 (x) sinωt,
(10)
где X 1 (x), X 2 (x) находятся из следующего выражения:
A sink x = X 1 (x) + iX 2 (x),
sinkl
2
k =
ω2
ω
− i α 2.
2
a
a
(11)
Перейдем теперь к пределу при α → 0:
u˜(x,t) = lim u(x, t) = A
α→0
где k˜= ω. a
sink˜x
cosωt.
˜
sinkl
(12)

11.

Уравнение свободных колебаний струны без начальных
условий
Из этого следует, что u˜является решениемуравнения:
2
∂2u
2∂ u
=a 2,
2
∂t
∂x
(13)
u(0, t)= 0,
u(l, t) = A cosωt.
(14)
при граничных условиях:
Но решение уравнения при α = 0 не всегда существует. Его нет
при
πn
ω = ωn = a.
l
С физической точки зрения, при таком значение ω наступает
резонанс.

12.

Пример промежуточной асимптотики
Сравним решения задачи без начальных условий и задачи с
начальными условиями дляуравнения
2
a ∂ u(x, t)= ∂ u(x, t) + e µt cosσ x,
∂t
∂x 2
где x ∈ R, µ ≥ 0.
(15)

13.

Пример промежуточной асимптотики
В случае задачи без начальных условий, решение имеет вид
u(x, t)=
e µt cos σ x
.
aµ + σ 2
(16)
В случае задачи с начальными условиями
u(x, 0) = 0,
решение имеет вид
σ2
eµt − e−t a
u + (x, t)=
aµ +σ 2
cosσx.
(17)

14.

Пример промежуточной асимптотики
Решение u(x, t) называется промежуточной асимптотикой
решения u + (x, t), если выполняется соотношение
lim ||u(x, t) − u + (x, t)||µ = 0,
t→+∞
где
||f (t)||µ = sup ||e −µt f (t)||,
t∈R
µ ≥ 0.
(18)

15.

Используя (16) и (17), найдем следующий предел
σ2
u + (x, t) = lim eµt − e−t a
lim
t→ ∞
t → ∞ u(x, t)
eµt
= 1.
Тогда из (19) следует (18), так как
∥ u(x, t) − u + (x, t) ∥ µ =
1
∥1 −
aµ + σ 2
u + (x, t)
∥
u(x, t) µ
Таким образом (19) показывает асимптотику u(x, t) для
u + (x, t).
(19)