Эконометрика. Корреляционнорегрессионный анализ

1. ЭКОНОМЕТРИКА

Корреляционнорегрессионный анализ

2. Корреляционный анализ

• Метод, применяемый тогда, когда данные
наблюдений или эксперимента можно
считать случайными и выбранными из
совокупности, распределенной по
многомерному нормальному закону
• Основная задача корреляционного анализа выявление связи между переменными
путем точечной и интервальной оценки
различных (парных, множественных,
частных) коэффициентов корреляции

3. Коэффициент корреляции:

• Формула:
r
xy x y
x y
,
r 1
• Оценка значимости с помощью t-критерия
Стьюдента:
t
r n 2
1 r
2
t ( , n 2 )
• n-2 – число степеней свободы
• α – уровень значимости

4. Пример для выборки из двухмерной нормально распределенной генеральной совокупности

• n = 122, r = 0,4, α = 0,05
• значение t-критерия Стьюдента:
t
r n 2
1 r
2
0,4 122 2
1 0,4
• tкр (0,05; 120)=1,98 < 4,78
• r – значимо отличается от 0
2
4,78

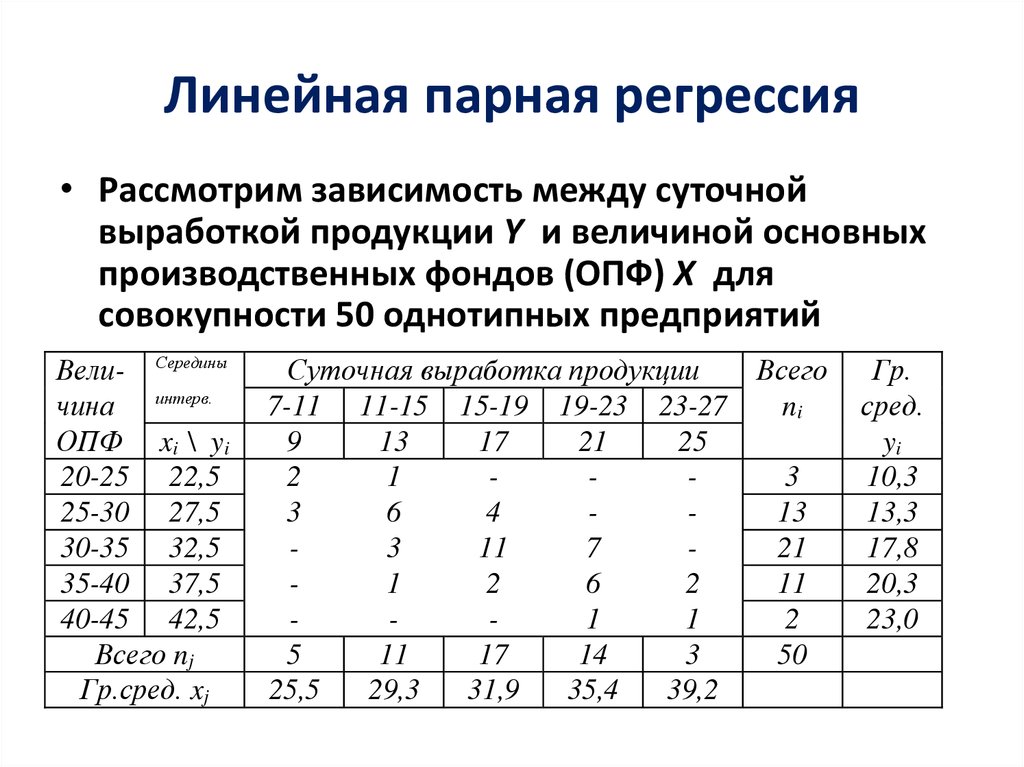
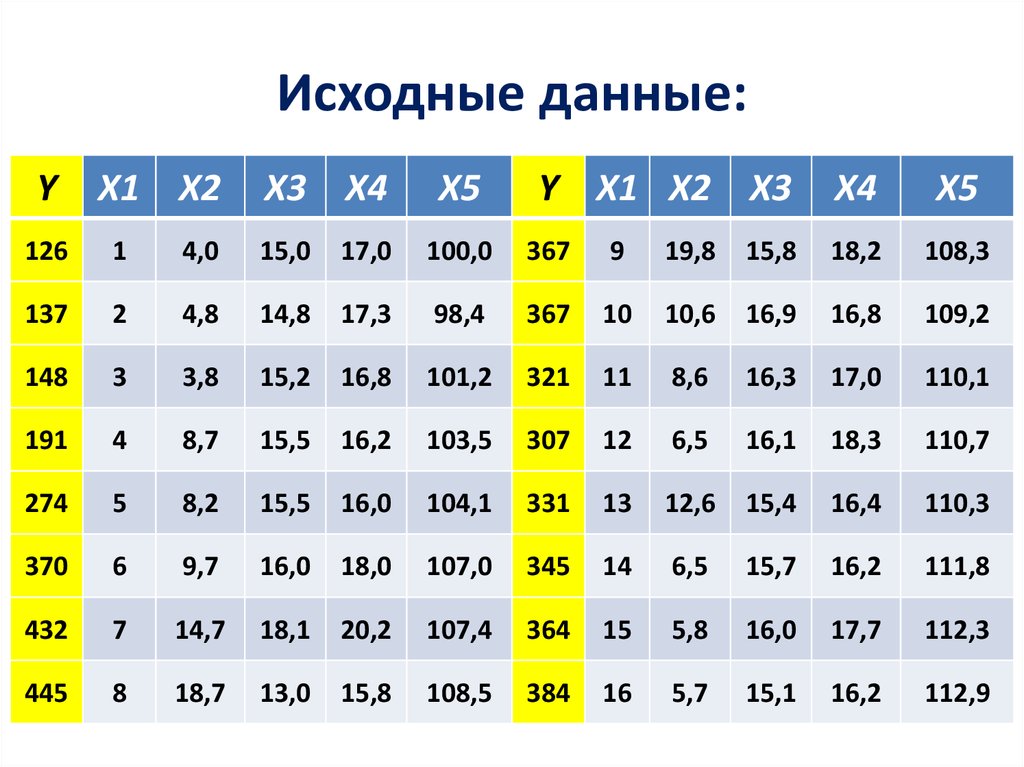
5. Линейная парная регрессия

• Рассмотрим зависимость между суточной
выработкой продукции Y и величиной основных
производственных фондов (ОПФ) X для
совокупности 50 однотипных предприятий
Вели- Середины
чина интерв.
ОПФ xi \ yi
20-25 22,5
25-30 27,5
30-35 32,5
35-40 37,5
40-45 42,5
Всего nj
Гр.сред. xj
Суточная выработка продукции
7-11 11-15 15-19 19-23 23-27
9
13
17
21
25
2
1
3
6
4
3
11
7
1
2
6
2
1
1
5
11
17
14
3
25,5
29,3
31,9
35,4
39,2
Всего
ni
3
13
21
11
2
50
Гр.
сред.
yi
10,3
13,3
17,8
20,3
23,0

6. Линейная парная регрессия: МНК

• Метод наименьших
квадратов:
l
S
(b
i 1
0
b1xi yi ) 2 ni min.
• Параметры уравнения регрессии находим из
системы нормальных уравнений:
l
l
b0 n bi xi ni yi ni ,
i 1
i 1
l
l
l
2
b
0 xi ni b1 xi ni xi yi ni .
i 1
i 1
i 1
• Уравнение регрессии: