Similar presentations:
Дифференциальное исчисление функции одной переменной
1. Дифференциальное исчисление функции одной переменной
2. 1. Функция
• 1.1. Некоторые математические символы.• Для краткой записи – кванторы.
• 1. => - квантор следования. (α => β – означает: из
α следует β)
• 2. - квантор эквивалентности (α эквивалентно
β). В формулировке теорем символ соответствует
словам «необходимо и достаточно» или «тогда и
только тогда».
• 3. - квантор общности. Запись ( х:α) означает:
« для любого х справедливо утверждение α.
3.
• 4. - квантор существования. Запись ( х:α)означает: существует по крайней мере один такой
Х для которого справедливо предложение α.
• 1.2. Множества
• Множество – первоначальное понятие.
A,B,C,…X,Y,Z.
• Элементы множества: a,b,c,..x,y,z.
• Конечное множество.
• Бесконечное множество.
• Пустое множество
4.
• Элемент принадлежит данному множеству:• α А, элемент не принадлежит данному
множеству: α А.
• Пересечение и объединение множеств.
А В С
А В С
• Вещественные числа.
• Целые положительные числа 1,2,3,4… образуют
мн-во натуральных чисел. N.
5.
• Все числа видаm
(m N , n N )
n
• а также 0 образуют мн-во рациональных чисел: С.
• Иррациональные числа: Q
• Множество вещественных чисел:
R C Q
• геометрически изображаются точками на
числовой оси. Ось: прямая, указано
положительное направление, начало отсчета и
отрезок, длина кот. принята за единицу длины.
6.
• Абсолютная величина вещественного числа• Модуль.
х
определяется соотношениями:
х, если х 0
х
х, если х 0
-х= х
x= х
x
x<0
x>0
• Геометрически: модуль х – расстояние от точки х
до 0
7.
• Из определения:х2 х1 , если х2 х1
х2 х1
х( х2 х1 ), если х2 х1
• Независимо от взаимного расположения точек –
модуль представляет собой расстояние между
ними.
• Промежутки. Окрестности.
• Открытый интервал – (а,в) или ]a,b[ это
множество вещественных чисел, удовл.усл.
а x b
8.
• Замкнутый интервал: [a,b],а x b
Полуоткрытые интервалы.
Это конечные промежутки.
Бесконечные промежутки:
Множество вещественных чисел R обозначается
символом: ( ; )
• Далее:
( x (a; )) ( x a)
( x ( ; в ]) ( x b)
9.
• Окрестность точки: числовое множество• Пусть 0
• По определению:
R (a)
R (a) (a , a ) или
( x R (a)) (a x a )
• Геометрически – это отрезок длины 2
• с серединой в точке а без включения концевых
точек. Конечная точка.
а-
а
а+
R
10.
• Введем три бесконечные точки, определив их0
окрестности.
1
• 1).
R ( ) ( , ) или
1
( x R ( )) ( x )
R ( )
0
1
11.
1R ( ) ( , ) или
1
( x R ( )) ( x )
1
1
R ( ) ( , ) ( , ) или
1
( x R ( )) ( х )
1
1
12.
• Левая и праваяопределению:
окрестности. По
R (а) (а , а)
R (a) (a, a )
• Функция
• Определение. Если каждому элементу х Х ставится в
соответствие единственный элемент у Y, то это
соответствие называется функцией (отображением),
определённой на множестве Х со значениями в
множестве Y. Элемент х называется аргументом, а
множество Х – областью определения функции f(х).
Элемент у, поставленный в соответствие элементу х
называется значением функции f в точке х. Обозначение:
у = f(х).
13.
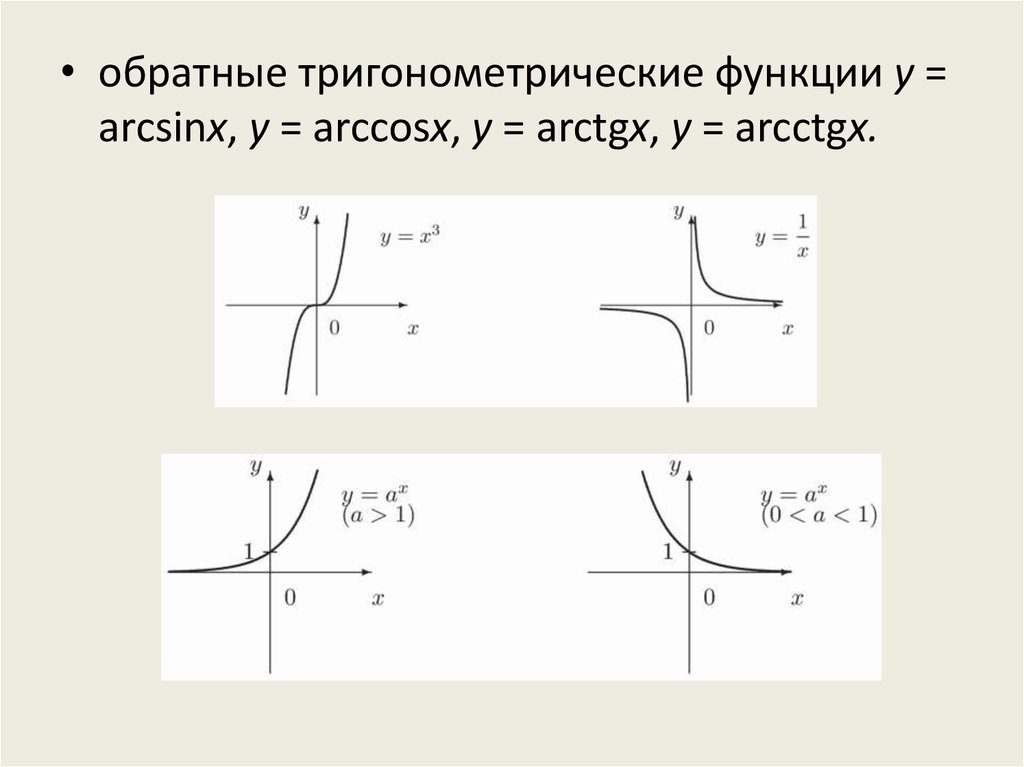
К основным элементарным функции относятся:
степенная функция y = xα, α R, α 0;
показательная функция у =ах, а 0, а 1;
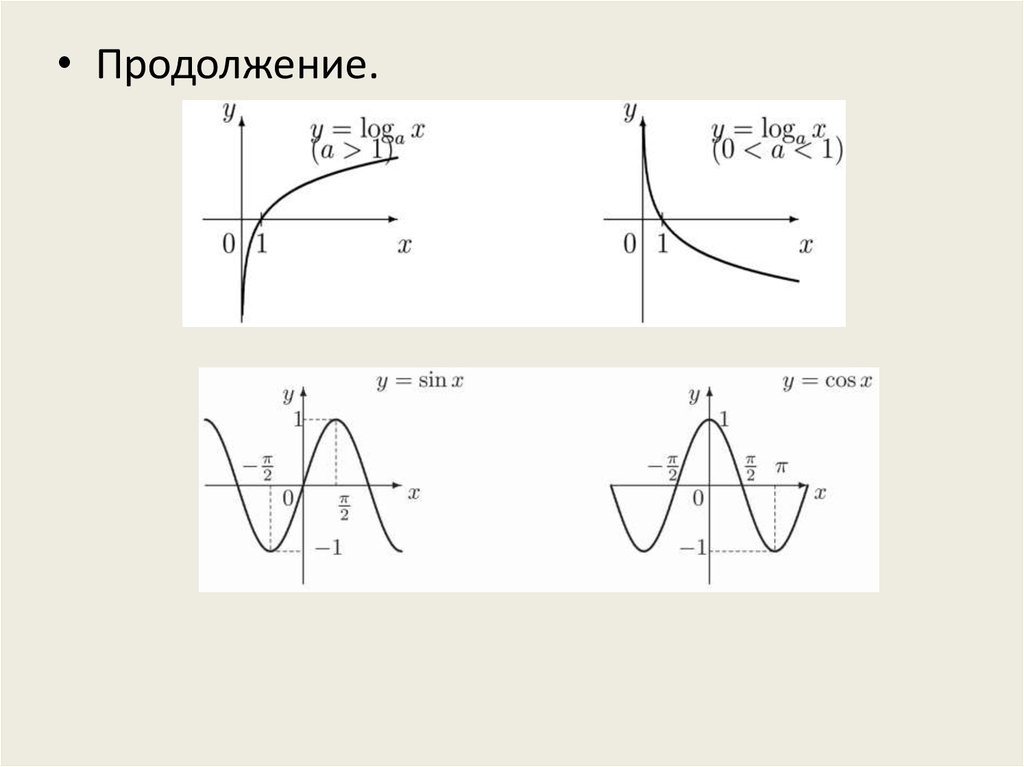
логарифмическая функция у = logах, а 0, а 1;
тригонометрические функции y = sinx, y = cosx,
y = tgx, y = ctgx;
14.
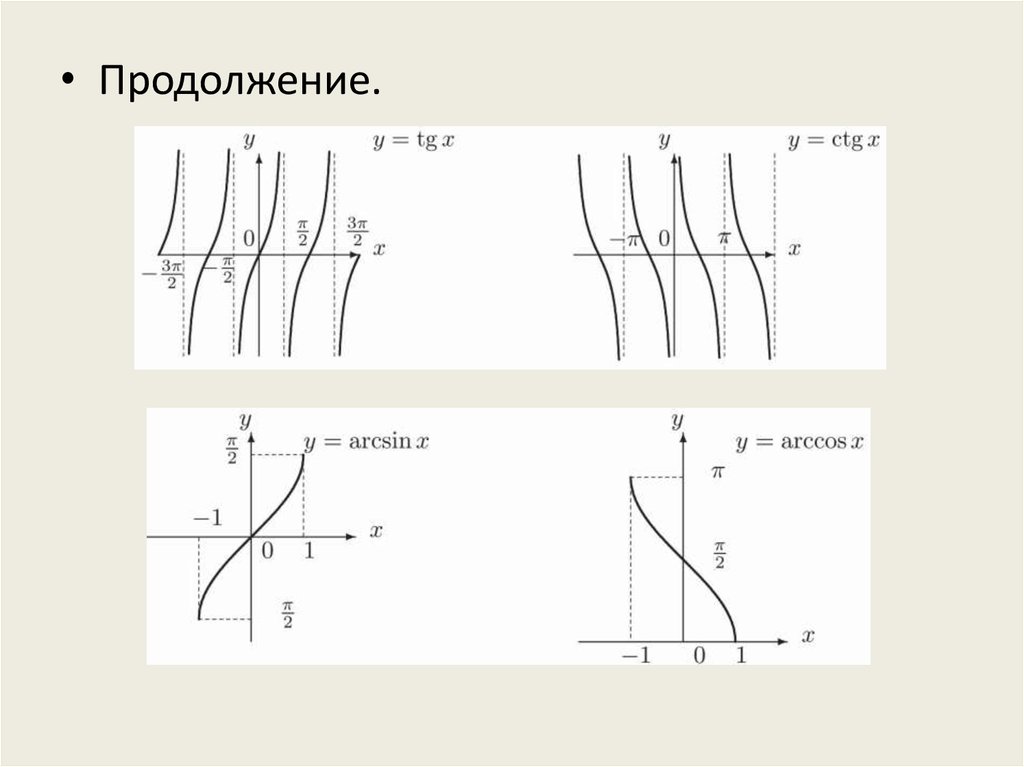
• обратные тригонометрические функции y =arcsinx, y = arccosx, y = arctgx, y = arcctgx.
15.
• Продолжение.16.
• Продолжение.17.
• arctgx, arcctgx:Если у = f(и), и = (x), то функция y = f(φ(x))
называется сложной функцией (функцией от
функции, суперпозицией функций) аргумента х;
аргумент u функции f называется
промежуточным. Например, если y u и U=sinx
• то суперпозицией этих функций является y sin x
.
18.
• Свойства функций.• Функция называется чётной, если f(–x) = f (x), и
нечётной, если f (–x) = – f (x). Например, x, x3, 1/x,
sinx, tgx, ctgx, arcsinx, arctgx (cм.рис.) – нечётные
функции, а x2, cosx – чётные функции.
• Функция f(x) называется возрастающей на Х, если
большему значению аргумента соответствует
большее значение функции, т.е.
• х1, х2 Х, х1 х2 f(x1) f(x2),
• и убывающей на Х, если
• х1, х2 Х, х1 х2 f(x1) f(x2).
19.
• Если неравенства нестрогие, то функцииназываются соответственно неубывающей и
невозрастающей. Возрастающие, убывающие,
невозрастающие и неубывающие на Х функции
называются монотонными. Например, ах, logах
(см. рис.) – монотонные функции, возрастающие
при а 1 и убывающие при 0 < а < 1.
• Функция f(x) называется ограниченной на Х, если
существует число М 0, при котором выполняется
• f (x) М для х Х. Например, sinx, cosx (см.
рис.), arcsinx, arccosx, arctgx, arcctgx –
ограниченные функции.
20.
• Функция f(x) называется периодической, еслисуществует Т 0, при котором выполняется
f(х + Т) = f(x) для всех х R. Т – период функции,
число nТ также является ее периодом.
• Рациональные и дробно-рациональные функции
• Целая рациональная функция (многочлен,
полином) имеет вид
Pn ( x) a0 x n a1x n 1 a2 x n 2 ... an 1x an
• n N.
• Если a является корнем многочлена, то
Pn ( x) ( x a) Pn 1 ( x)
21.
• Дробно–рациональная функция(рациональная дробь) имеет вид
Qm ( x)
Pn ( x)
• где Qm ( x), Pn ( x)
• – многочлены степени m и n
соответственно. При m < n рациональная
дробь называется правильной, в противном
случае – неправильной.


















 mathematics
mathematics








