7.73M

Category:

physics

Стохастическое описание систем генной регуляции

1.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
7.1 Природа шума в генной регуляции
7.2 Стохастическое описание
7.2 Алгоритм Гиллеспи
7.3 Модифицированный алгоритм Гиллеспи
7.3 Эффект подкритического возбуждения колебаний
1 of 31

2.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
Много ли молекул воды в стакане?
Число молекул в 1 см3 воды при
нормальных условиях ~ 1023 штук
Лорд Кельвин: если зачерпнуть из океана стакан воды и
пометить все молекулы в стакане, а затем вылить обратно в
океан и тщательно всё перемешать, то зачерпывая еще раз в
стакане будет порядка 100 молекул из первого стакана.
Современный вариант байки: 65 млн лет назад капля слюны
динозавра упала в ручей, а затем растворилась в мировом
океане. Если сейчас зачерпнуть стакан из океана, то в нем
будет 4-5 молекул слюны динозавра.
2 of 31

3.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
Для описания движения в такой среде
нет необходимости следить за каждой
молекулой в отдельности - вводится
понятие сплошной среды
Уравнение Навье - Стокса:
Это детерминистское описание системы,
игнорирующее флуктуации
3 of 31

4.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
4 of 31
Много ли молекул участвует
в генной регуляции?
Количество молекул, вовлечённых во
внутриклеточные биохимические реакции ~
102 -103 (скорость работы РНК-полимеразы
до 50 нуклеотидов /сек)
... пятьдесят (50) нуклеотидов
в секунду!

5.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
Роль случайных флуктуаций в
генетических системах очень важна!
Требуется стохастическое описание
динамической системы
5 of 31

6.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
6 of 31
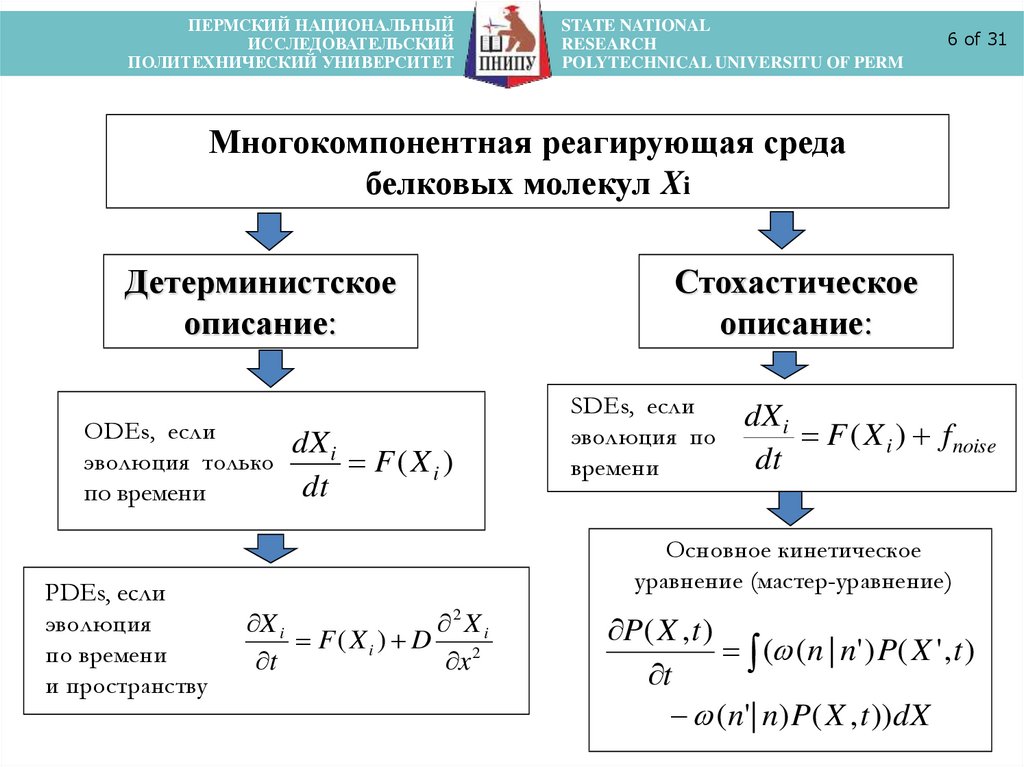
Многокомпонентная реагирующая среда
белковых молекул Xi
Детерминистское
описание:
ODEs, если
эволюция только
по времени
PDEs, если
эволюция
по времени
и пространству
dX i
F(Xi )
dt
Стохастическое
описание:
SDEs, если
эволюция по
времени
dX i
F ( X i ) f noise
dt
Основное кинетическое
уравнение (мастер-уравнение)
X i
2 X i
F(Xi ) D
t
x 2
P( X , t )
( (n | n' ) P( X ' , t )
t
(n'| n) P( X , t ))dX

7.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
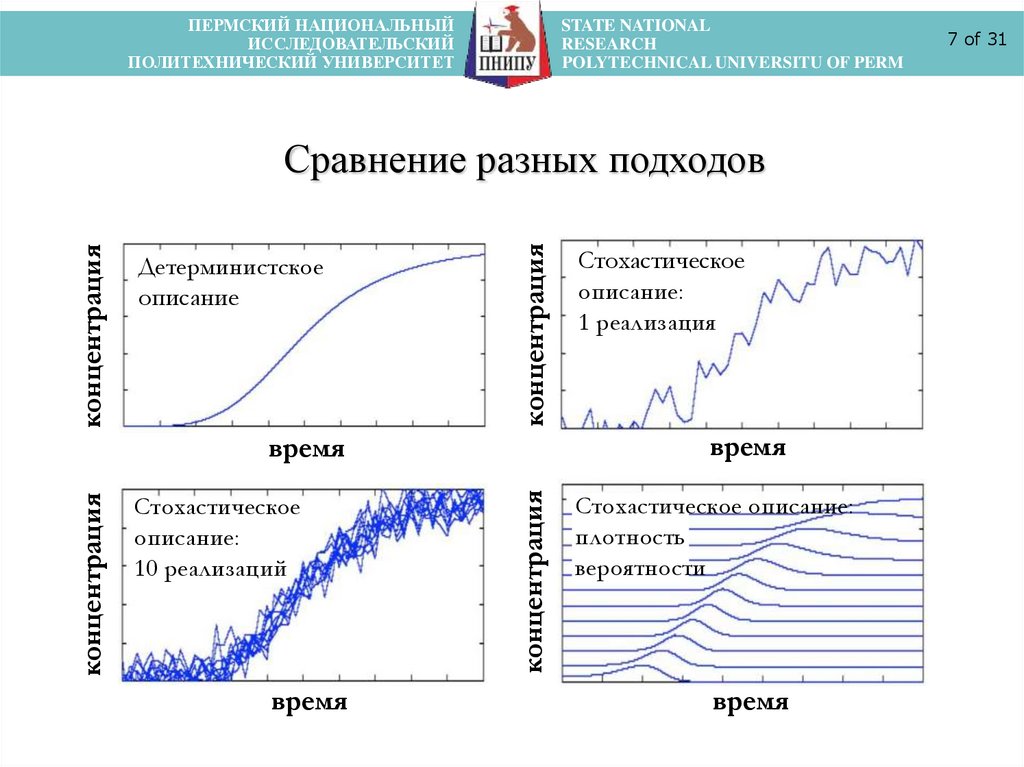
Детерминистское
описание
концентрация
концентрация
Сравнение разных подходов
время
время
концентрация
концентрация
время
Стохастическое
описание:
10 реализаций
Стохастическое
описание:
1 реализация
Стохастическое описание:
плотность
вероятности
время
7 of 31

8.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
Полезная книга:
К.В. Гардинер «Стохастические методы в
естественных науках»
8 of 31

9.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
Мастер-уравнение
(основное кинетическое уравнение):
рабочий пример из книги К. Гардинера
9 of 31

10.

11.

12.

13.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
13 of 31
Мастер-уравнение
легко получить, но практически
невозможно решить, так как оно
представляет собой сложнейший тип
интегро-дифференциальных уравнений
в частных производных

14.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
14 of 31
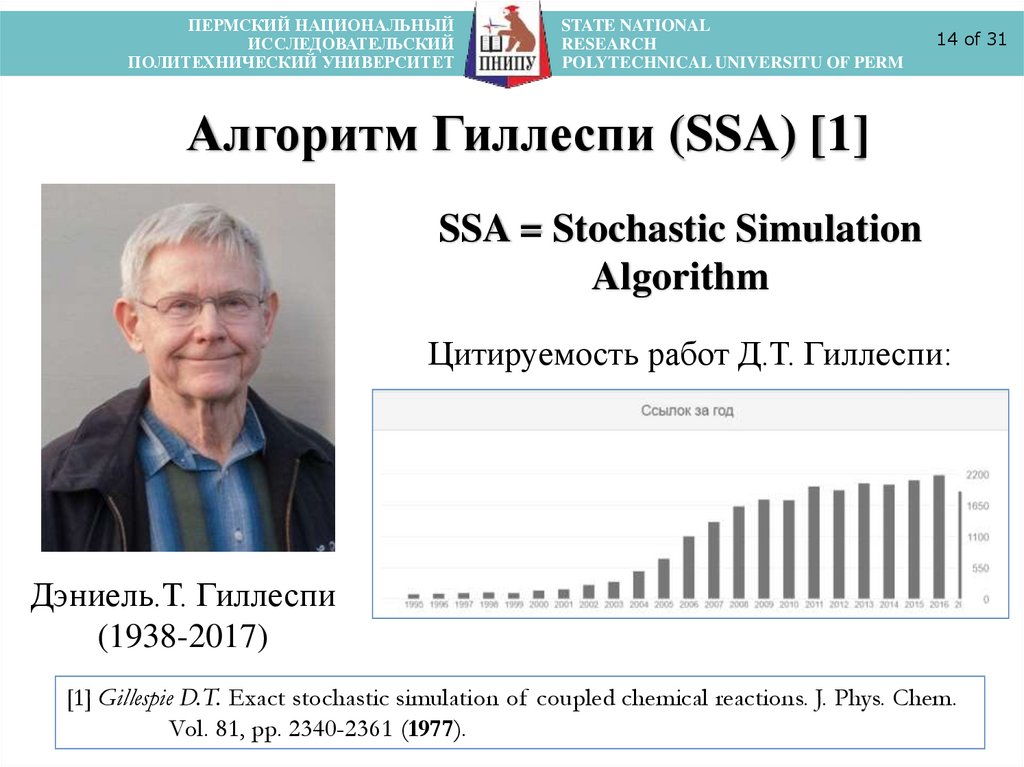
Алгоритм Гиллеспи (SSA) [1]
SSA = Stochastic Simulation
Algorithm
Цитируемость работ Д.Т. Гиллеспи:
Дэниель.Т. Гиллеспи
(1938-2017)
[1] Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem.
Vol. 81, pp. 2340-2361 (1977).

15.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
Популярность алгоритма Гиллеспи
(данные на ноябрь 2019 г.)
15 of 31

16.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
16 of 31
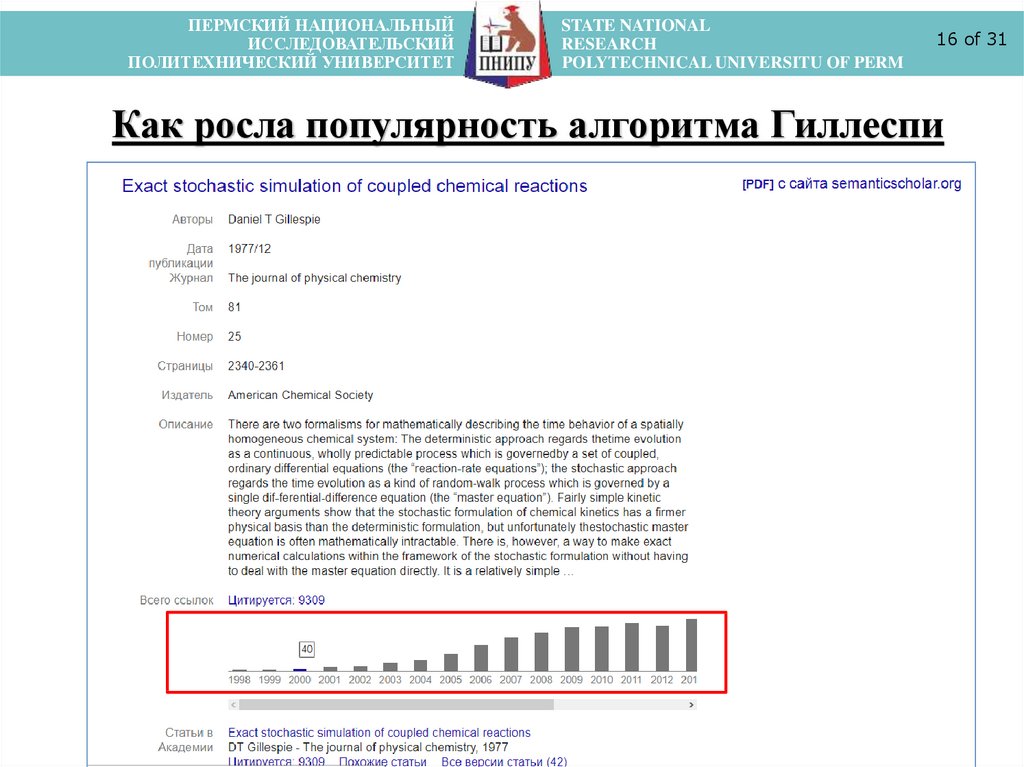
Как росла популярность алгоритма Гиллеспи

17.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
Взрывной рост интереса к алгоритму Гиллеспи
(SSA) связывается с возникновением
и резким ростом
интереса к малоразмерным химическим
системам с небольшим числом действующих
молекул (
)
в нулевые годы 21 века
17 of 31

18.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
18 of 31
Алгоритма Гиллеспи
работает ТОЛЬКО на случай
шаги по времени
t1
t2 t3
Гипотеза Маркова [2] постулирует, что состояние системы в
момент времени t зависит только от предыдущего состояния
системы в момент времени t t и не зависит от состояний
системы, которые она занимала до этого момента
[2] Марков А.А. Распространение закона больших чисел на величины, зависящие друг от
друга. Известия физико-математического общества при Ка-занском университете, 1906,
2-я серия, Том 15, с. 135-156

19.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
19 of 31
Блок-схема алгоритма из статьи Гиллеспи [1]
[1] Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem.
Vol. 81, pp. 2340-2361 (1977).

20.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
20 of 31
Алгоритм Гиллеспи [1]
численно воспроизводит решения
мастер-уравнения для химической кинетики
имеется N химических компонент X { X 1 , X 2 ,..., X N )
имеется M химических каналов (реакций)
вычисляется вероятность для каждого канала a 1...M
a
вычисляется полная вероятность a0
генерирование двух случайных чисел r1, r2 [0,1]
вычисление времени до следующей реакции t J ln r1 / a0
* 1
*
нахождение канала для следующей реакции a r2a0 a
1
1
[1] Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem.
Vol. 81, pp. 2340-2361 (1977).

21.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
21 of 31
Основные элементы алгоритма
Вопрос №1: когда произойдет следующая реакция?
В пределе
получим:

22.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
22 of 31
Основные элементы алгоритма
Вопрос №1: когда произойдет следующая реакция?
Ответ: следующая реакция произойдет через время
r1
t ln
a0

23.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
23 of 31
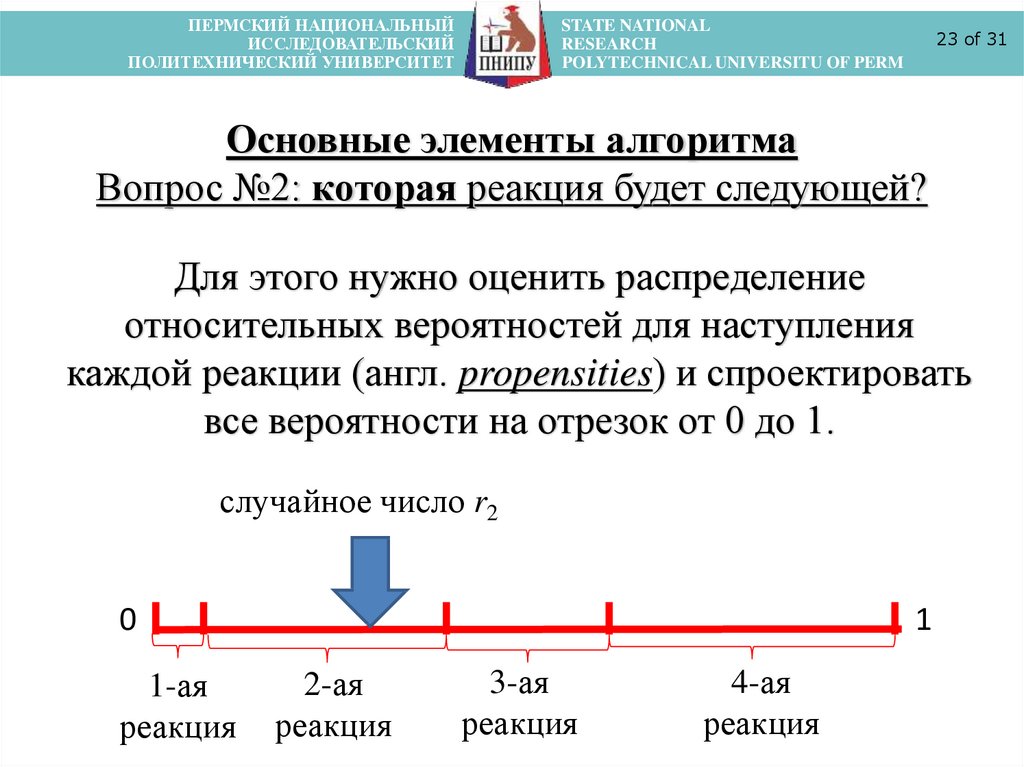
Основные элементы алгоритма
Вопрос №2: которая реакция будет следующей?
Для этого нужно оценить распределение
относительных вероятностей для наступления
каждой реакции (англ. propensities) и спроектировать
все вероятности на отрезок от 0 до 1.
случайное число r2
0
1-ая
реакция
1
2-ая
реакция
3-ая
реакция
4-ая
реакция

24.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
24 of 31
Основные элементы алгоритма
Вопрос № 3: как вычислять пропенсити (склонность,
предпочтительность) каждого реакционного канала?
Ответ [1]:
склонность = скорость реакции * вероятность реакции
(вероятность реакции вычисляется по закону
действующих масс)
[1] Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem.
Vol. 81, pp. 2340-2361 (1977).

25.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
25 of 31
Модификация алгоритма Гиллеспи
на случай запаздывающей обратной связи
(немарковские процессы) [3]
отложенная реакция
шаги по времени
t1
t2 t3
[3] Bratsun D., Volfson D., Hasty J., Tsimring L. Delay-induced stochastic oscillations in gene
regulation. PNAS, Vol.102, No.41, 2005, pp. 14593-14598.

26.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
26 of 31
Популярность алгоритма у исследователей
(данные на ноябрь 2019 г.)

27.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
27 of 31
Стохастическое описание для модели №1
A
t
Xt
B
X t
t
C
X t
t
Детерминистское описание:
x A Bx (t ) Cx(t )
Пусть P(n,t) – вероятность того, что система в момент времени t
обладает n молекулами белка в мономерной форме
Мастер – уравнение (основное кинетическое уравнение):
dP(n, t )
A( P(n 1, t ) P(n, t )) B((n 1) P(n 1, t ) nP(n, t ))
dt
C m( P(n 1, t; m, t ) H (n) P(n, t; m, t )) n 0..
n 0
При больших временах запаздывания мастер-уравнение расцепляется:
P(n, t; m, t ) P(n, t | m, t ) P(m, t ) P(n, t ) P(m, t )

28.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
28 of 31
Точное решение мастер-уравнения
для автокорреляционной функции
A (T )
K (T )
B 1 e
e T e (T ) ,
(T )
0 T
T
B ( T N )
B (T ' N )
( N ) C (T ' ) e
e
dT ' , N T N 1
N
1
(B )
C
B2 C 2

29.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
29 of 31
Фурье-спектр сигнала
*
2
0.157
2
аналитическое решение
численное решение
Алгоритм
верифицирован!

30.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
30 of 31
Взаимодействие запаздывания и шума:
возбуждение сложных квазирегулярных колебаний в
подкритической области (Модель №3)
Модель динамики белка с обратной запаздывающей связью
область
неустойчивости
k
X X
XD
1
k
X D
X X
1
k
k
D0 X D
D1 D1
D0 X D
2
2
A
D0t P t
D0t P t X t
B
X

31.

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
STATE NATIONAL
RESEARCH
POLYTECHNICAL UNIVERSITU OF PERM
31 of 31
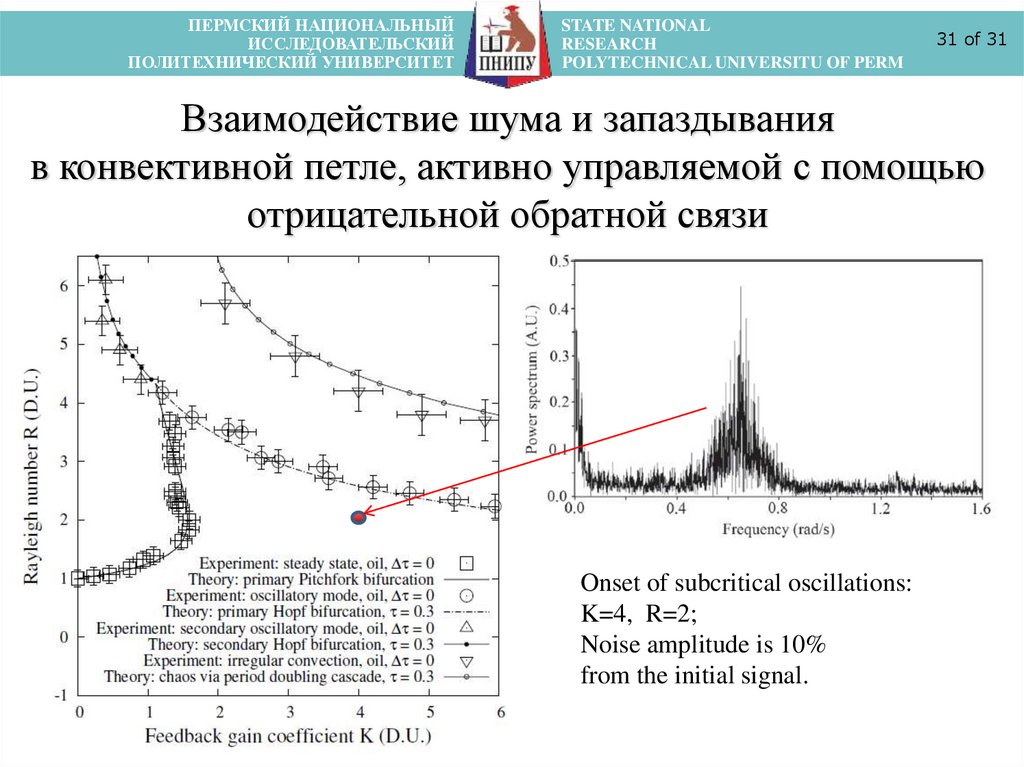
Взаимодействие шума и запаздывания
в конвективной петле, активно управляемой с помощью
отрицательной обратной связи
Onset of subcritical oscillations:
K=4, R=2;
Noise amplitude is 10%
from the initial signal.

English Русский Rules