Similar presentations:
Бесконечно убывающая геометрическая прогрессия
1.
Бесконечно убывающагеометрическая прогресси
«Алгебра есть не что иное, как математический язык,
приспособленный для обозначения отношений между
количествами».
И. Ньютон
2. 1) Закончите предложение:
1 вариант2 вариант
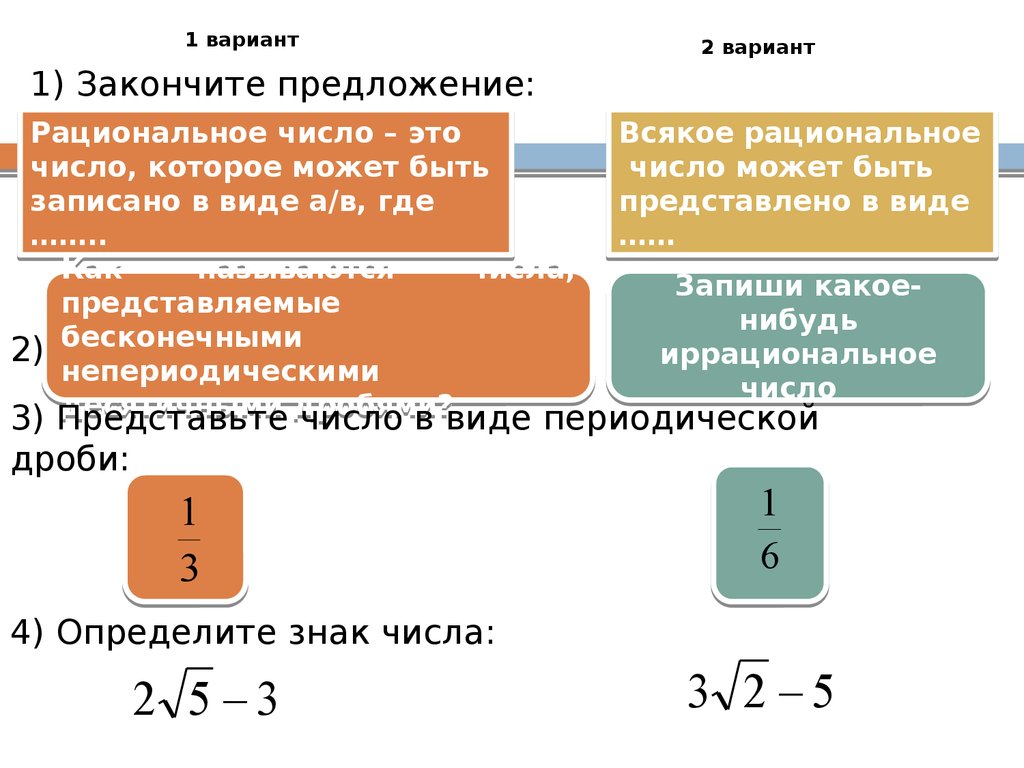
1) Закончите предложение:
Рациональное число – это
Всякое рациональное
число, которое может быть
число может быть
записано в виде а/в, где
представлено в виде
……..
……
Как
называются
числа,
Запиши какоепредставляемые
нибудь
бесконечными
2)
иррациональное
непериодическими
число
десятичными
дробями?
3) Представьте число в виде периодической
дроби:
1
3
1
6
4) Определите знак числа:
2 5 3
3 2 5
3.
знать :Знания и определение
навыки учащихся:
геометрической
прогрессии;
определение
бесконечно
убывающей
геометрической
прогрессии;
формулу суммы бесконечно
убывающей
геометрической
прогрессии;
уметь применять формулу суммы
бесконечно убывающей геометрической
прогрессии
§3
( в частности при записи бесконечной
периодической
десятичной дроби в виде обыкновенной)
Бесконечно убывающая
геометрическая
прогрессия
4. 1. Определение
Геометрическаяпрогрессия
–
такая числовая последовательность
b1,
b2,
b3,
…,
bn
,
…,
что для всех натуральных
n
выполняется равенство bn+1 = bnq ,
где bn≠0, q≠0
5.
Формула n-го членагеометрической
последовательности:
n 1
n
1
b b q
6.
Формула суммы первыхчленов:
n
b1 1 q
Sn
, где _ q 1
1 q
n
S n b1 n, где _ q 1
7.
2. Геометрическая прогрессияназывается бесконечно убывающей,
если модуль её знаменателя меньше
1 (|q|<1)
Формула суммы
бесконечно убывающей
геометрической
прогрессии
b1
S
1 q
8.
2. Геометрическая прогрессияназывается бесконечно убывающей,
если модуль её знаменателя меньше
1 (|q|<1)
Формула суммы
бесконечно убывающей
геометрической
прогрессии
b1
S
1 q







 mathematics
mathematics