Сумма бесконечной убывающей геометрической прогрессии

1.

Сумма бесконечной
убывающей геометрической
прогрессии

2.

Софизм-это головоломка,
хитроумное высказывание, хорошо
замаскировавшее ошибку.
Нахождение ошибок в
математических софизмах помогла
развитию математики. Теперь мы с
вами рассмотрим софизм Зенона

3.

Чтобы пройти путь в один километр, нужно
непременно миновать его середину,
утверждал Зенон. Само по себе это
утверждение верно.
Но далее Зенон рассуждает так: если мы
дошли до середины пути,
перед нами остается еще полпути, у которого
есть своя середина. И так без конца. Сколько
бы мы ни шли, впереди всегда есть какая-то
не пройденная часть пути, у которой есть
своя середина.

4.

Мы получим
последовательность:
1 1 1 1 1
; ; ; ; ;....
2 4 8 16 32

5.

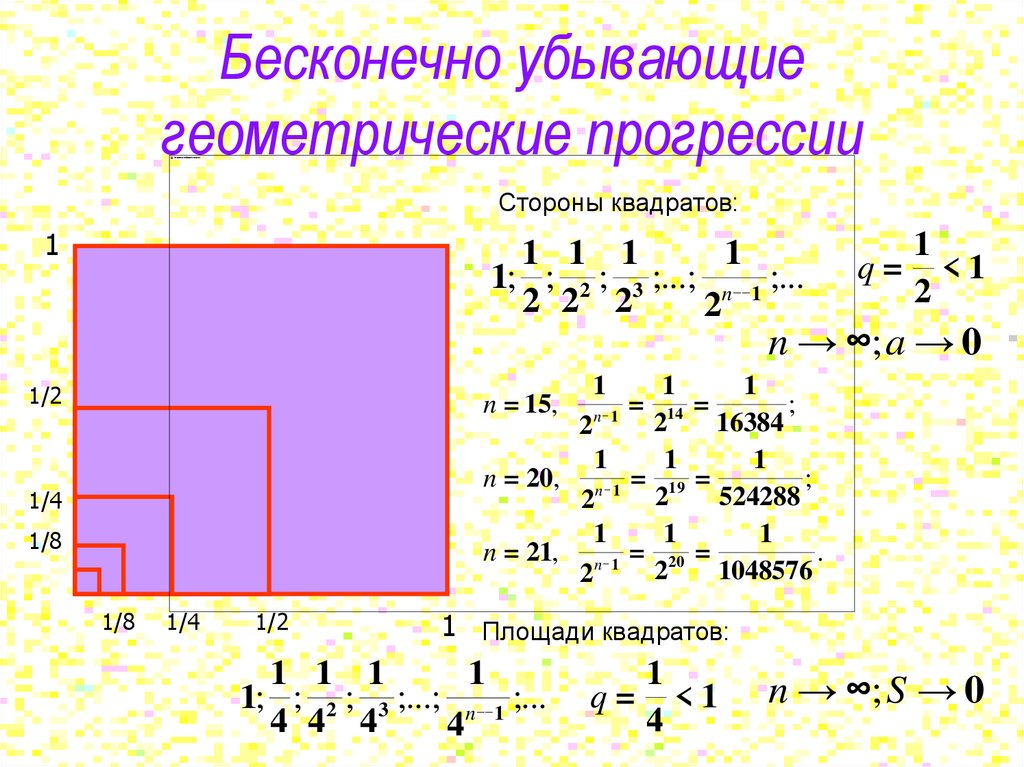
Бесконечно убывающие
геометрические прогрессии
Стороны квадратов:
1
1 1 1
1
1; ; 2 ; 3 ;...; n __ 1 ;...
2 2 2
2
1
q= <1
2
n → ∞; a → 0
1
1
1
=
=
;
_
14
n 1
2
16384
2
1
1
1
n = 20, n _ 1 = 19 =
;
2
524288
2
1
1
1
n = 21, n _ 1 = 20 =
.
2
1048576
2
1/2
n = 15,
1/4
1/8
1/8
1/4
1/2
1 Площади квадратов:
1 1 1
1
1; ; 2 ; 3 ;...; n __ 1 ;...
4 4 4
4
1
q= <1
4
n → ∞; S → 0

6.

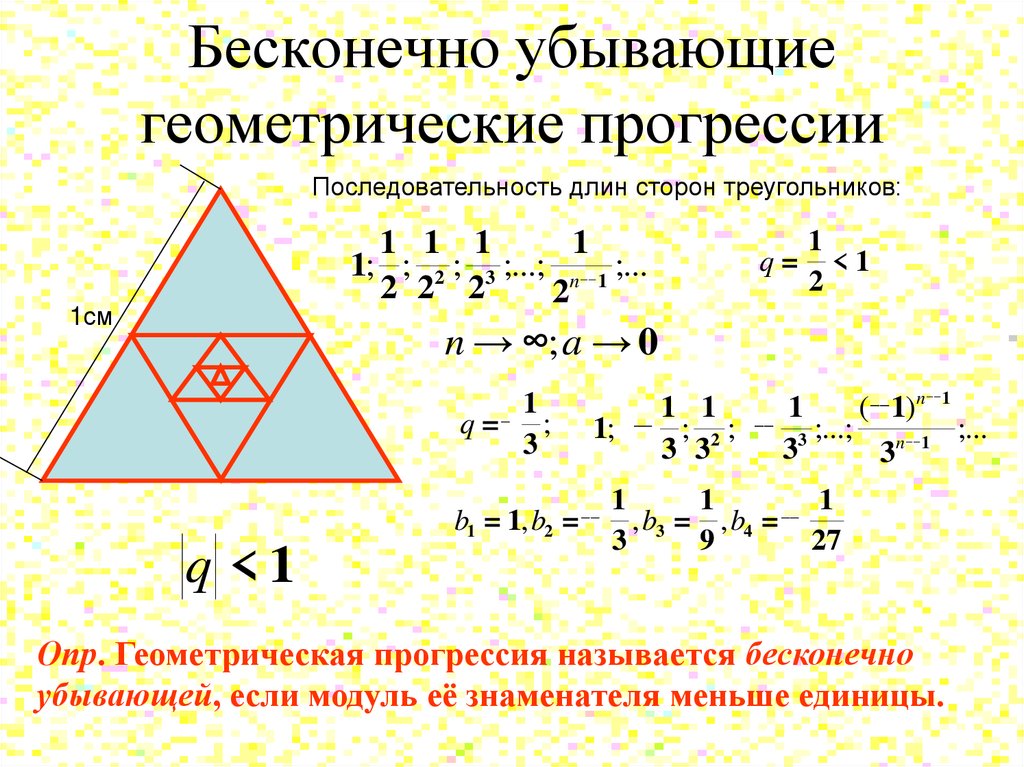
Бесконечно убывающие
геометрические прогрессии
Последовательность длин сторон треугольников:
1 1 1
1
1; ; 2 ; 3 ;...; n __ 1 ;...
2 2 2
2
1см
q=
1
<1
2
n → ∞; a → 0
_ 1
q= ;
3
b1 = 1, b2 =
q <1
__
1;
__
__
n __ 1
1 1 __ 1
( 1)
; ;
;...; n __ 1 ;...
3 32
33
3
1
1
__ 1
,b = ,b =
3 3 9 4
27
Опр. Геометрическая прогрессия называется бесконечно
убывающей, если модуль её знаменателя меньше единицы.

7.

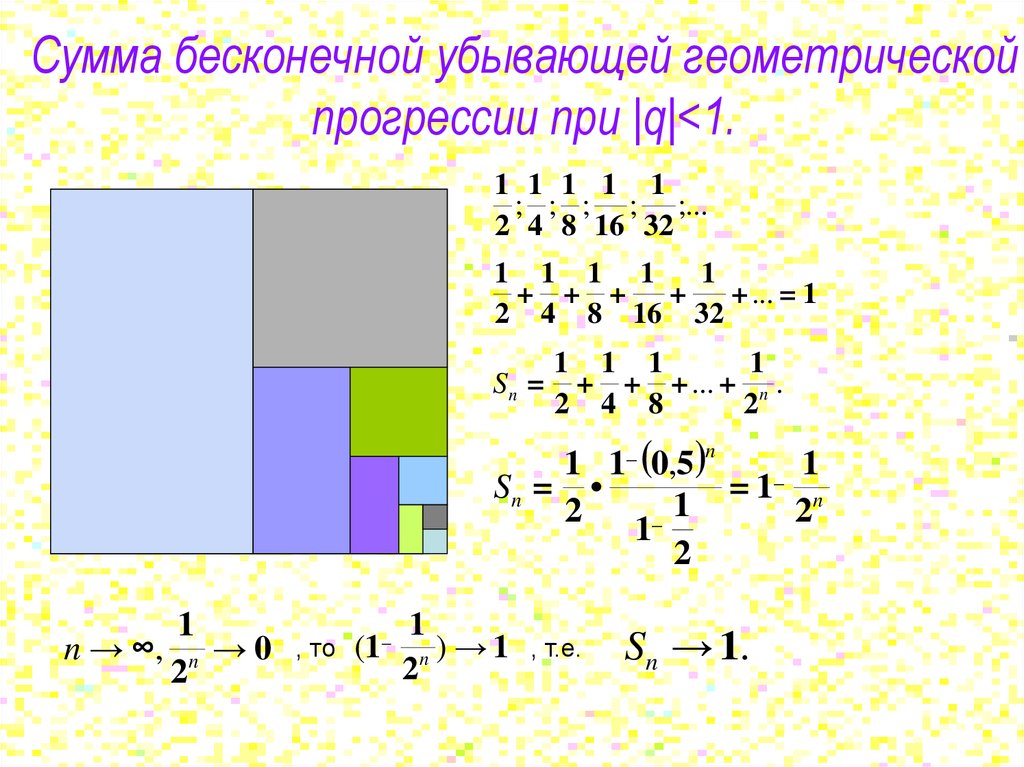
Сумма бесконечной убывающей геометрической
прогрессии при |q|<1.
1 1 1 1 1
; ; ; ; ;...
2 4 8 16 32
1 1 1 1
1
+ + + +
+ ... = 1
2 4 8 16 32
1 1 1
1
Sn = + + + ... + n .
2 4 8
2
1 1_ (0,5)n
_ 1
Sn =
=1 n
1
2
2
1_
2
1
n → ∞, n → 0
2
1
, то (1 n ) → 1 , т.е.
2
_
Sn → 1.

8.

Сумма бесконечной убывающей
геометрической прогрессии при |q|<1.
Опр. Суммой бесконечно убывающей геометрической
прогрессии называют число, к которому стремится сумма её
первых n членов при n →
∞
b1 (1_ q n )
Sn =
.
_
1 q
q < 1, то
b1
Sn = _
1 q
q → 0, при
n
_
b1
n
q
.
_
1 q
n → ∞.
b1
S= _
1 q
Поэтому
q <1
b1
n
q
→0
_
1 q

9.

Самопроверка
1). Является ли геометрическая прогрессия бесконечно
убывающей, если: b7= -30; b6= 15 ?
b7 _ 30 _
q= =
= 2;
b6
15
_
2 > 1,⇒ Г.П. не является бесконечно
убывающей
2). Найдите сумму бесконечно убывающей геометрической прогрессии:
-25; -5; -1;…
_
b1
1
25 _ 125 _ 1
_
S _ ; b1 25; q ; S
31 31,25
1
1 q
5
4
4
1_
5
3). Записать бесконечную десятичную периодическую дробь
0,(9) в виде обыкновенной дроби. 0,(9)=0,9999…=0,9+0,09+0,009+….
0, (9 ) =
9
9
9
+ 2 + 3 + ...
10 10 10
1
b1
0,9
0,9
q= ; S= _ ; S= _
=
= 1.
10
1 q
1 0,1 0,9
0, (9) = 1