Similar presentations:
Руководство для выполнения графических работ по начертательной геометрии для студентов вузов
1.
Т Г Т У2.
3.
П.А. Острожков, М.А .Кузнецов, С.И. Лазаревдля студентов ВУЗов, обучающихся по направлениям техники
и технологии
4.
Графическая работа № 1Графическая работа № 2
Графическая работа № 3
Проверочный
тест
Приложение
5.
Графическая работа № 1Взаимное положение двух плоскостей.
Цель работы: закрепление знаний при
позиционных задач.
Задача
Задача №
№ 11
решении
Задача
Задача №
№ 22
6.
Задача № 11. В плоскости, заданной тремя точками
А,В,С (координаты точек смотри в
приложении) построить треугольник,
образованный горизонталью, фронталью и
профильной прямой. Начертить
полученный треугольник в натуральную
величину.
2. Построить плоскость, параллельную
заданной и отстоящую от нее на
расстоянии 50 мм.
7.
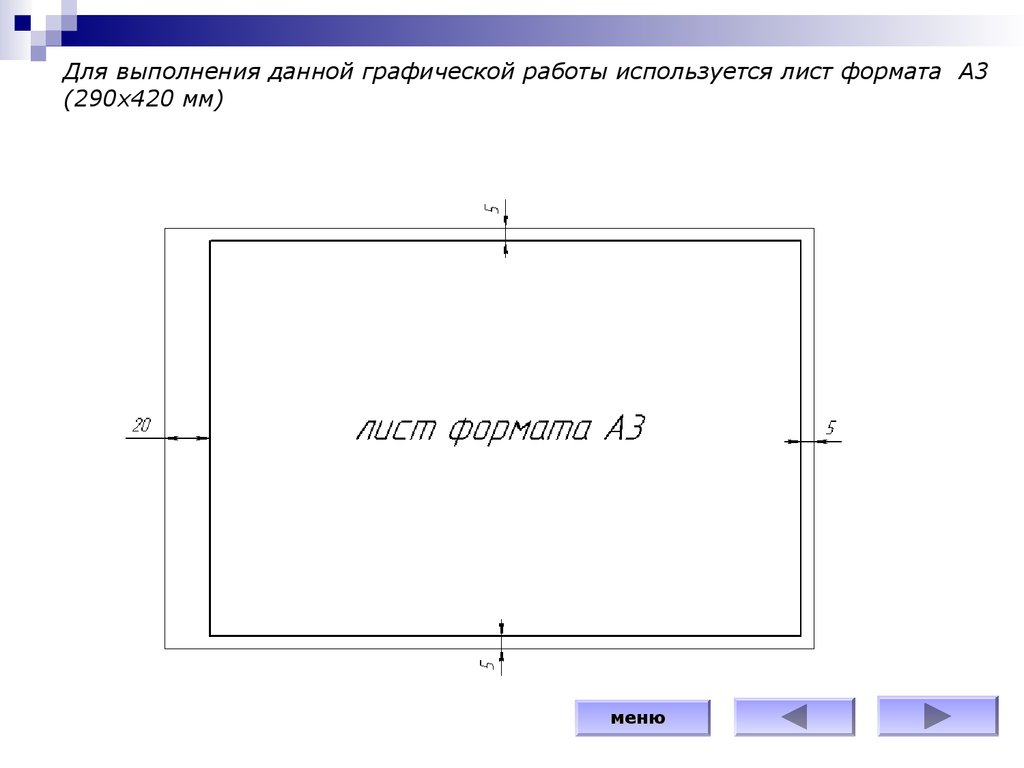
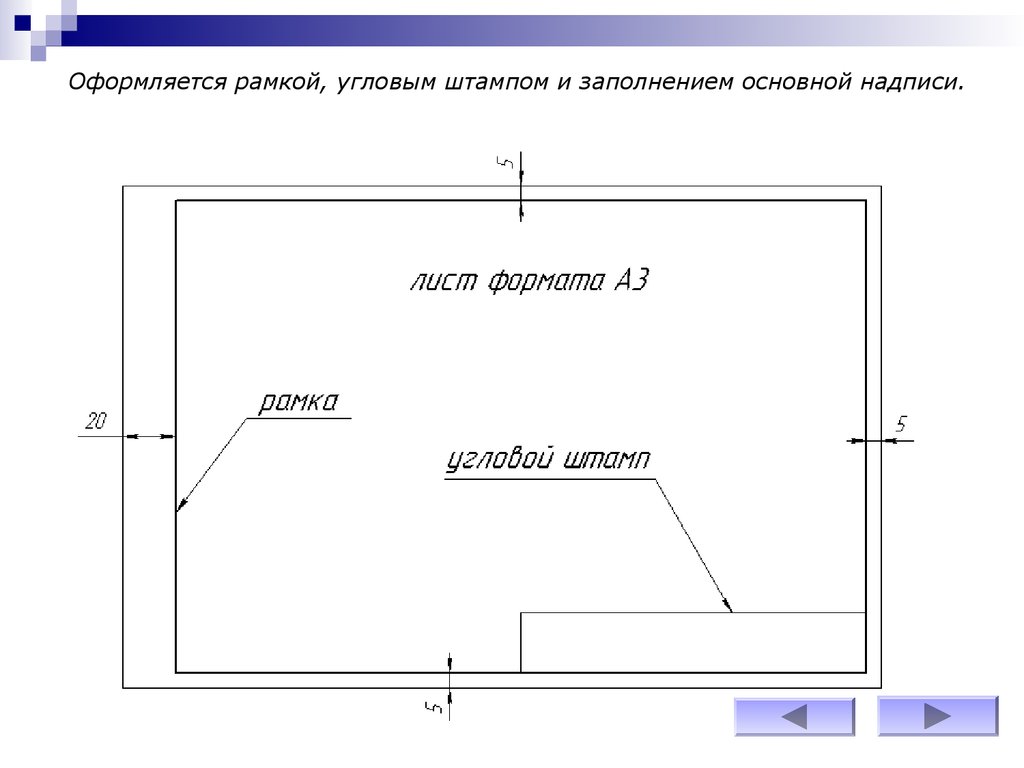
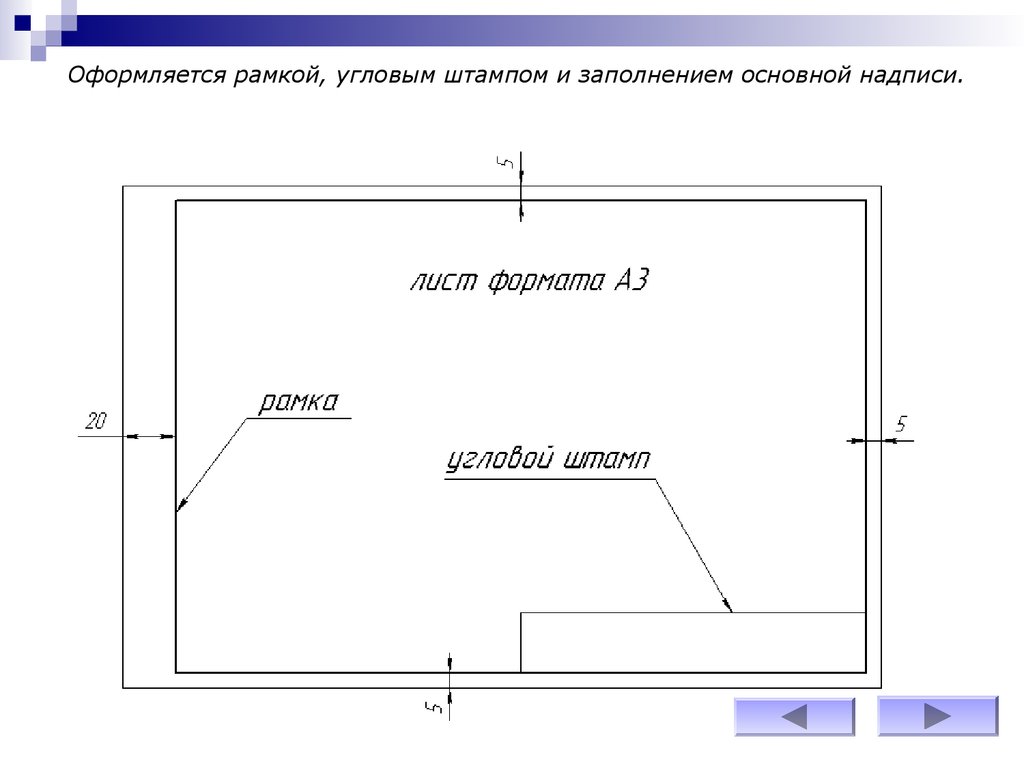
Для выполнения данной графической работы используется лист формата А3(290х420 мм)
меню
8.
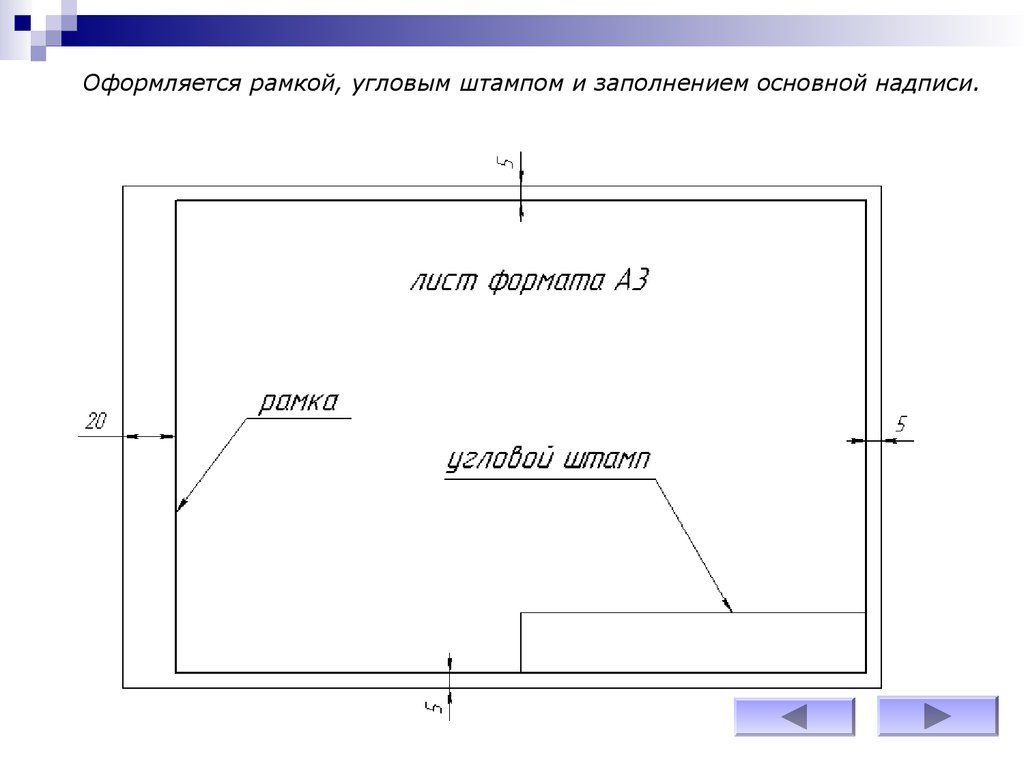
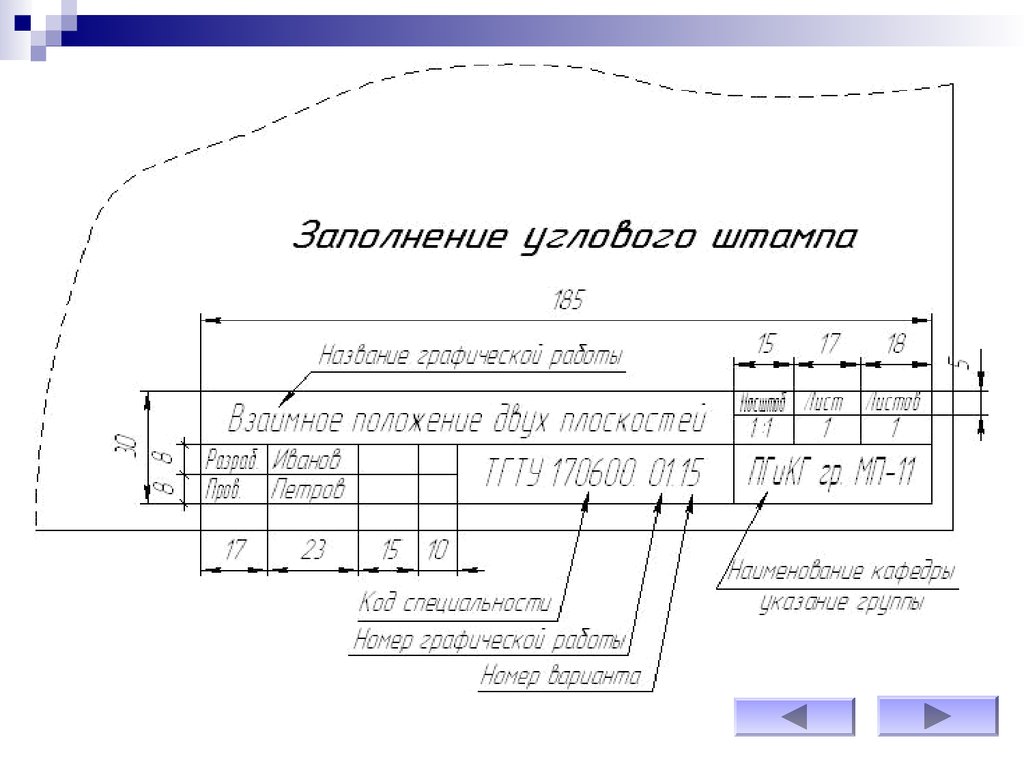
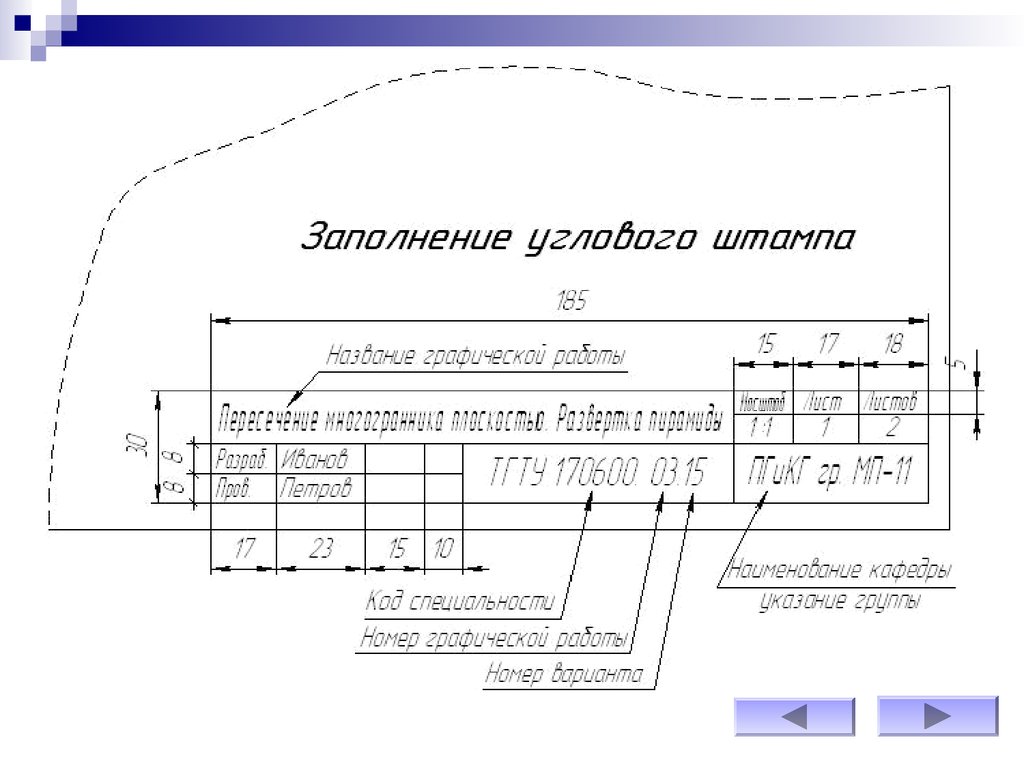
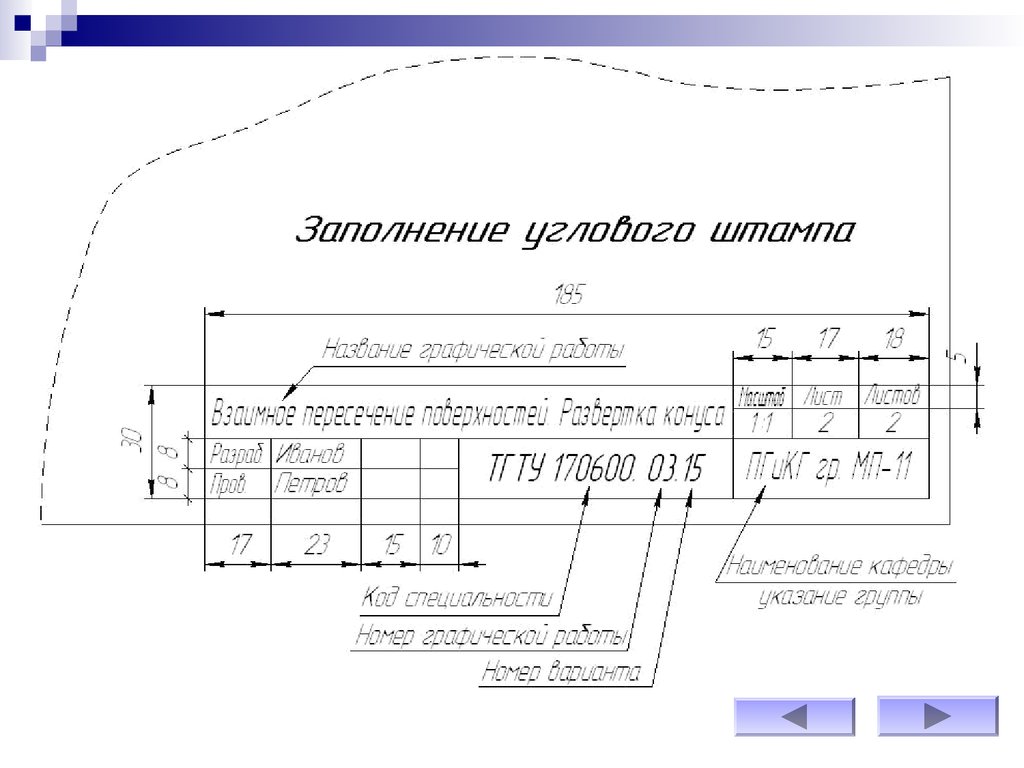
Оформляется рамкой, угловым штампом и заполнением основной надписи.9.
10.
Размечаем мысленно лист на 2 части11.
В левой части листа формата А3 намечаем оси координат.z
x
0
y
12.
Согласно координатам индивидуального задания отмечаем точки А, В и С –вершины ∆ АВС в координатных плоскостях.
B”
A”
z
C”
x
0
B’
A’
C’
y
13.
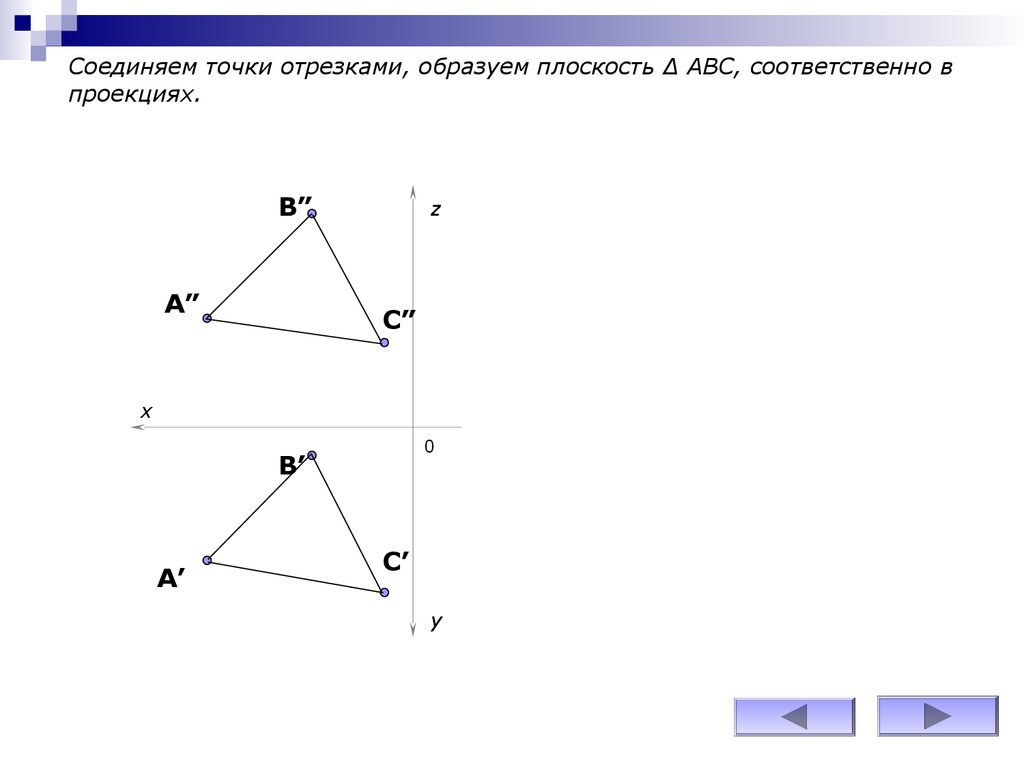
Соединяем точки отрезками, образуем плоскость ∆ АВС, соответственно впроекциях.
B”
A”
z
C”
x
0
B’
A’
C’
y
14.
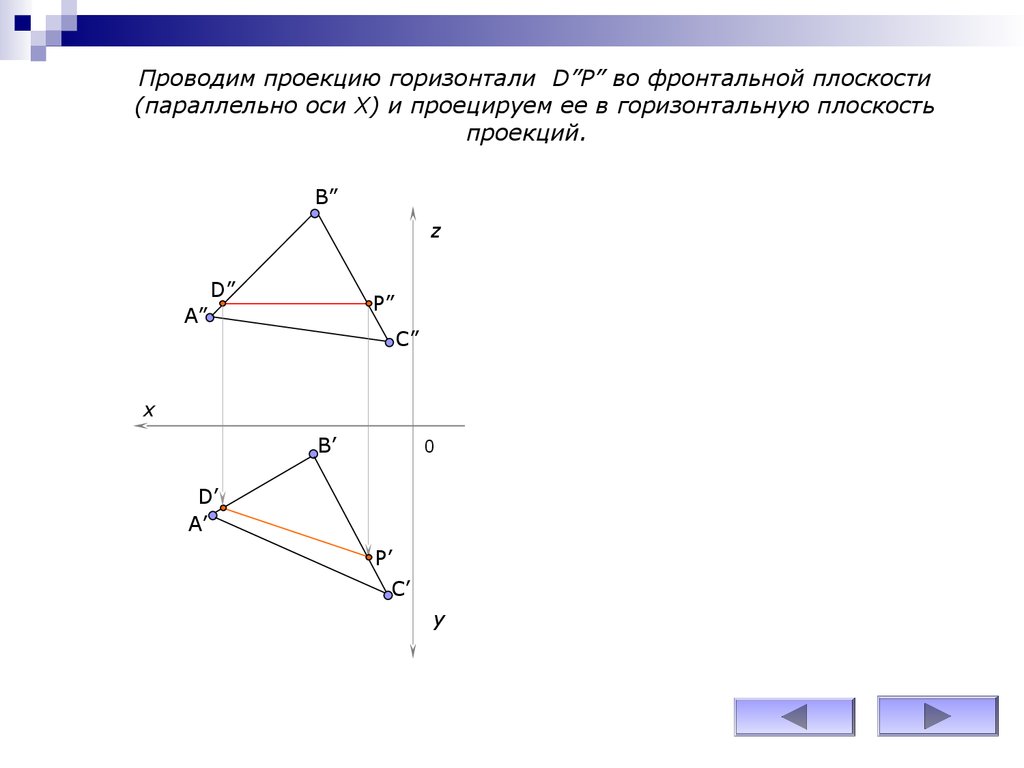
Проводим проекцию горизонтали D”P” во фронтальной плоскости(параллельно оси Х) и проецируем ее в горизонтальную плоскость
проекций.
B”
z
D”
P”
A”
C”
x
B’
0
D’
A’
P’
C’
y
15.
Проводим в горизонтальной плоскости проекции фронталь D’E’, затемпроводим профильную прямую. Образуем DEF, в котором с помощью
способа прямоугольного треугольника находим натуральную величину
катета EF.
B”
z
Е”
D”
A”
F”
P”
C”
x
0
B’
D’
A’
E*
Е’
F’ P’
C’
y
16.
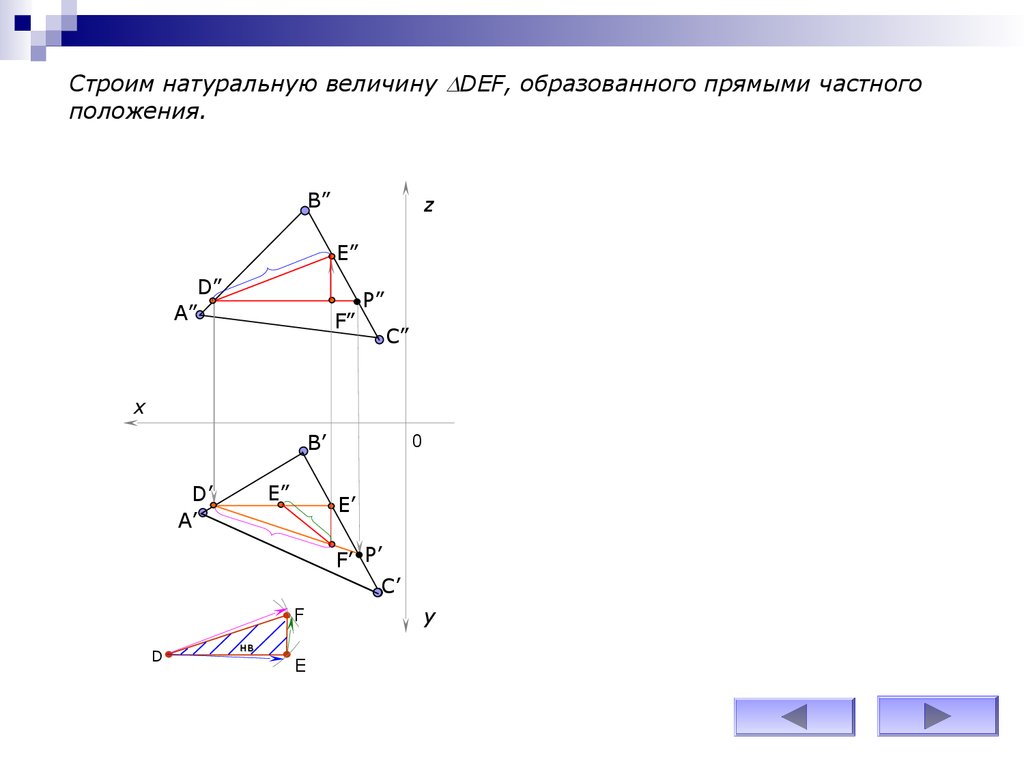
Строим натуральную величину DEF, образованного прямыми частногоположения.
B”
z
Е”
D”
A”
F”
P”
C”
x
0
B’
E”
D’
A’
Е’
F’ P’
C’
F
D
нв
E
y
17.
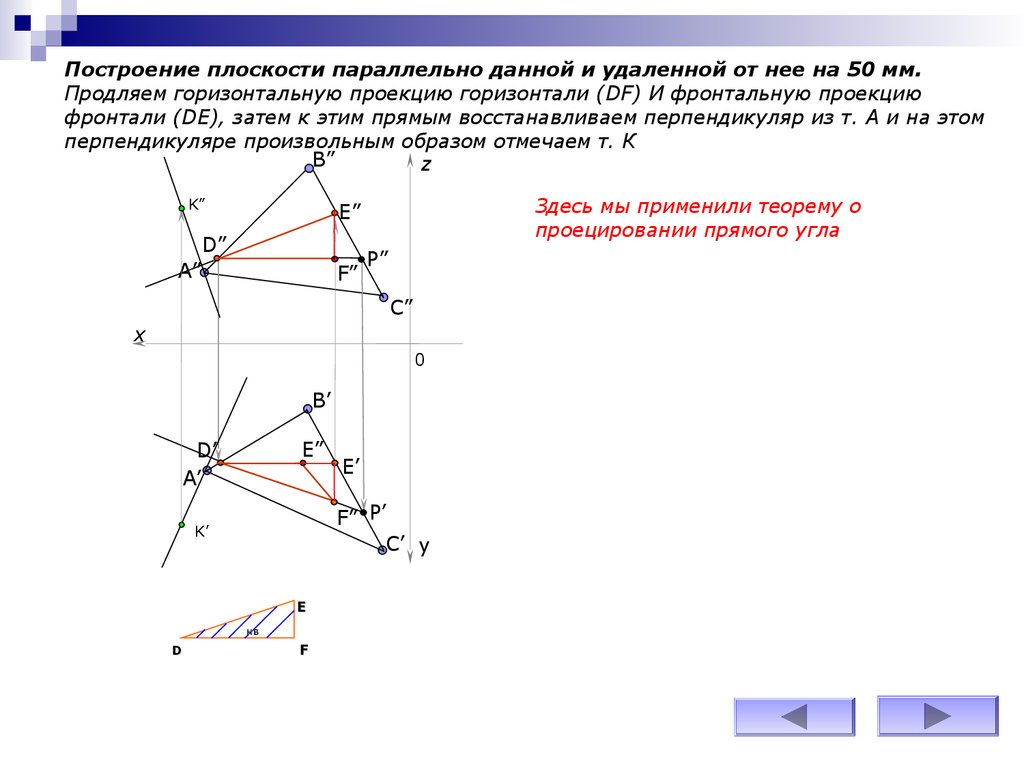
Построение плоскости параллельно данной и удаленной от нее на 50 мм.Продляем горизонтальную проекцию горизонтали (DF) И фронтальную проекцию
фронтали (DE), затем к этим прямым восстанавливаем перпендикуляр из т. А и на этом
перпендикуляре произвольным образом отмечаем т. К
B”
z
K”
Здесь мы применили теорему о
проецировании прямого угла
Е”
D”
A”
F”
P”
C”
x
0
B’
E”
D’
A’
F” P’
C’ y
K’
E
нв
D
Е’
F
18.
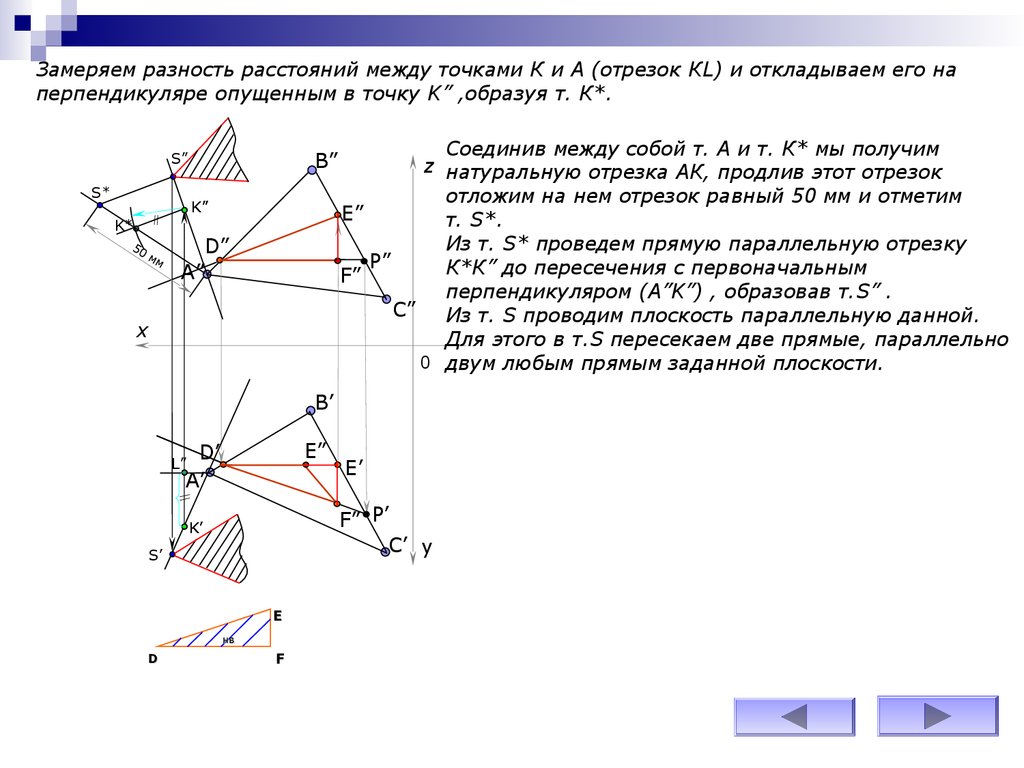
Замеряем разность расстояний между точками К и А (отрезок КL) и откладываем его наперпендикуляре опущенным в точку K” ,образуя т. К*.
B”
S”
S*
K”
K*
50
мм
D”
A”
x
Соединив между собой т. А и т. К* мы получим
z натуральную отрезка АК, продлив этот отрезок
отложим на нем отрезок равный 50 мм и отметим
Е”
т. S*.
Из т. S* проведем прямую параллельную отрезку
P”
К*К” до пересечения с первоначальным
F”
перпендикуляром (А”K”) , образовав т.S” .
C”
Из т. S проводим плоскость параллельную данной.
Для этого в т.S пересекаем две прямые, параллельно
0 двум любым прямым заданной плоскости.
B’
E”
D’
A’
L”
F” P’
C’ y
K’
S’
E
нв
D
Е’
F
19.
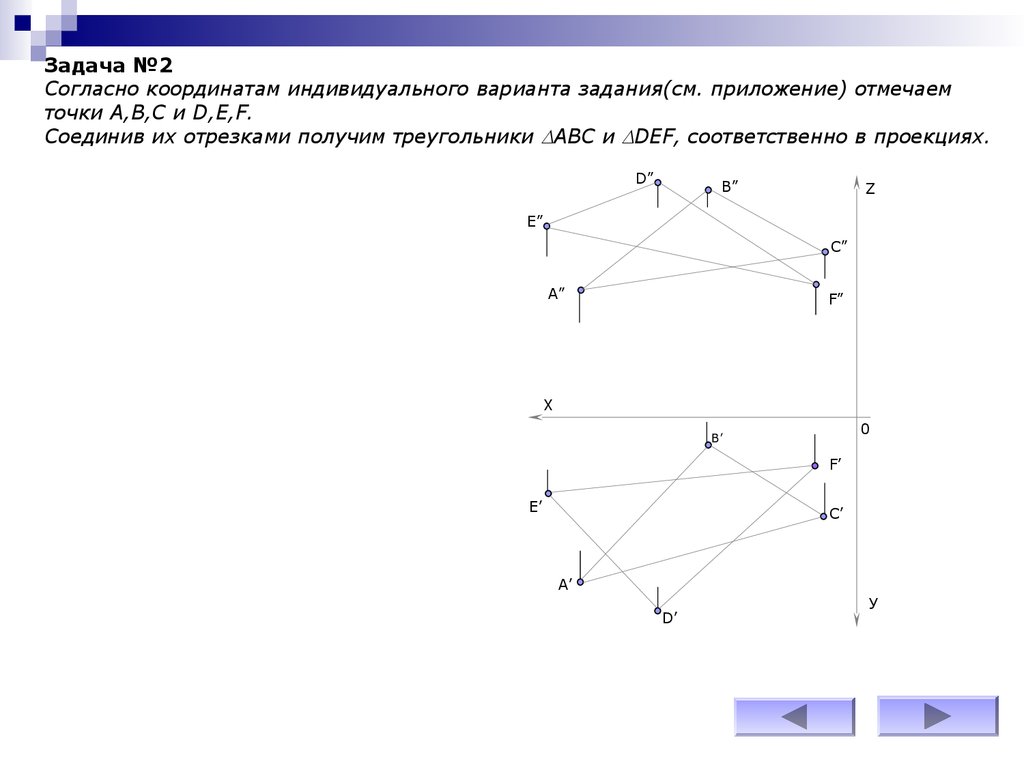
Задача №2Согласно координатам индивидуального варианта задания(см. приложение) отмечаем
точки А,В,С и D,E,F.
Соединив их отрезками получим треугольники АВС и DEF, соответственно в проекциях.
D”
B”
Z
E”
C”
A”
F”
X
0
B’
F’
E’
C’
A’
D’
У
20.
Отмечаем в горизонтальной плоскости проекции т.1 и т.2, точки пересечения стороны А’В’( АВС) соответственно со сторонами E’F’ и D’E’ DEF.
Проецируем т.1 и т.2 во фронтальную плоскость проекции на соответствующие прямые и
соединяем отрезком т.1 и т.2 между собой.
На пересечении прямой А”B” и отрезка 1”2” образуем т.К”, затем проецируем ее в
горизонтальную плоскость проекции на соответствующую прямую.
1”
E”
D”
B”
Z
K”
C”
2”
A”
F”
X
0
B’
2’
E’
K’
F’
C’
1’
A’
D’
У
21.
Во фронтальной плоскости проекции отмечаем т.3 и т.4, точки пересечения сторон А”В” иА”С” ( АВС) со стороной D”F” ( DEF).
Проецируем т.3 и т.4 в горизонтальную плоскость проекции на соответствующие стороны
треугольника, соединяем их между собой отрезком.
На пересечении отрезка 3’ 4’ со стороной D’F’, образуем т. L .
Проецируем т.L во фронтальную плоскость проекции на соответствующую сторону (D”F”).
D”
3”
1”
Соединив т.К и т.L между собой ,получим
искомую линию KL - линию пересечения
плоскостей, заданных треугольниками.
E”
B”
Z
K”
L”
2”
C”
4”
A”
F”
X
0
B’
2’
E’
F’
3’
K’
L’
C’
4’
1’
A’
D’
У
22.
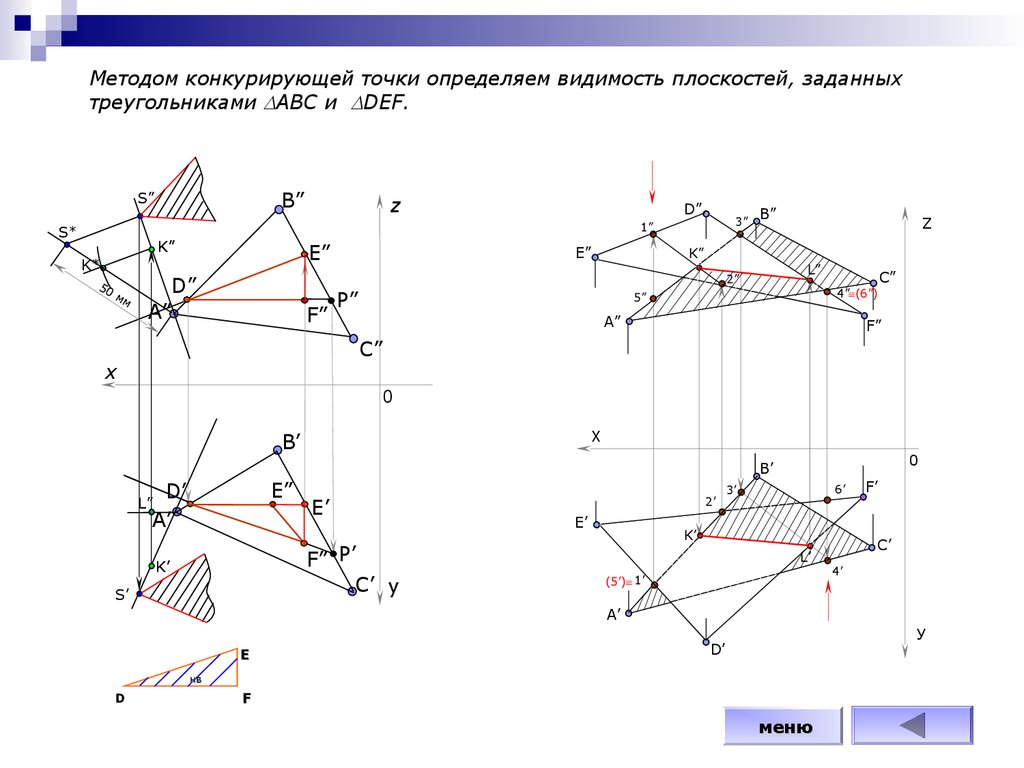
Методом конкурирующей точки определяем видимость плоскостей, заданныхтреугольниками АВС и DEF.
B”
S”
z
D”
3”
1”
S*
K”
K*
50
мм
Е”
E”
B”
K”
L”
2”
D”
A”
F”
Z
P”
C”
4” (6”)
5”
A”
F”
C”
x
0
X
B’
0
B’
E”
D’
A’
L”
Е’
F” P’
C’ y
K’
S’
2’
E’
6’
3’
K’
L’
(5’) 1’
F’
C’
4’
A’
E
У
D’
нв
D
F
меню
23. Графическая работа №2
Способы преобразования чертежаЦель работы: закрепление знаний и основных
приемов при решении метрических задач.
24.
Условие задачи.Дана пирамида SABCD с основанием АВСD (координаты
точек смотри в приложении) расположенным в
плоскости общего положения.
Требуется :
1.Методом вращения вокруг линии уровня определить
натуральную величину основания АВСD.
2.Методом плоско-параллельного перемещения
определить расстояние от вершины S до плоскости
основания АВСD.
3. Методом перемены плоскостей проекции определить
истинную величину двугранного угла при ребре ВC,
образованного основанием и боковой гранью
пирамиды.
25.
Для выполнения данной графической работы используется листформата А3 (290х420 мм)
26.
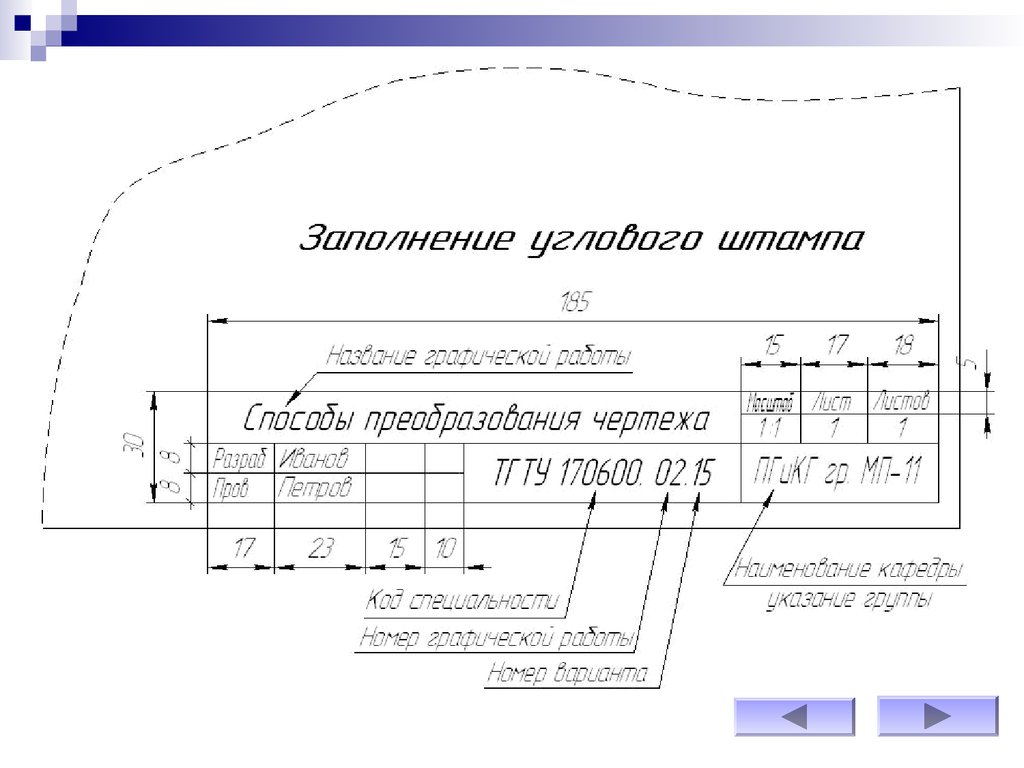
Оформляется рамкой, угловым штампом и заполнением основной надписи.27.
28.
ZB”
D”
L”
C”
S”
X
A”
0
S’
B’
D’
L’
C’
A’
У
Согласно индивидуального задания
отмечаем по координатам точки
S,А,В,С и D“,недостающую
координату т. D’ - определяем
построением.
Соединяем точки отрезками,
образуем плоскость основания
пирамиды ABCD.
29.
ZB”
L”
D”
C”
S”
H”
X
0
A”
S’
B’
D*
D’
RD
L’
C’
O’1
A’
ось вращ
.
H’
D
У
Задаемся осью вращения (линия
уровня-AH).
В горизонтальной плоскости
проекции из точки D’ опускаем
перпендикуляр на ось вращения
A’H’, на их пересечении образуем
центр вращения (т.О’1)
соответствующей точки D” .
Методом прямоугольного
треугольника получаем
натуральную величину радиуса
вращения точки D.
Вращаем т.D до пересечения с
перпендикуляром, на их
пересечении образуем т. D
30.
ZB”
L”
D”
C”
S”
H”
X
0
A”
S’
B’
D*
D’
RD
L’
B*
RB
C’
O’1
A’
O’2
O’3
H’
D
B
У
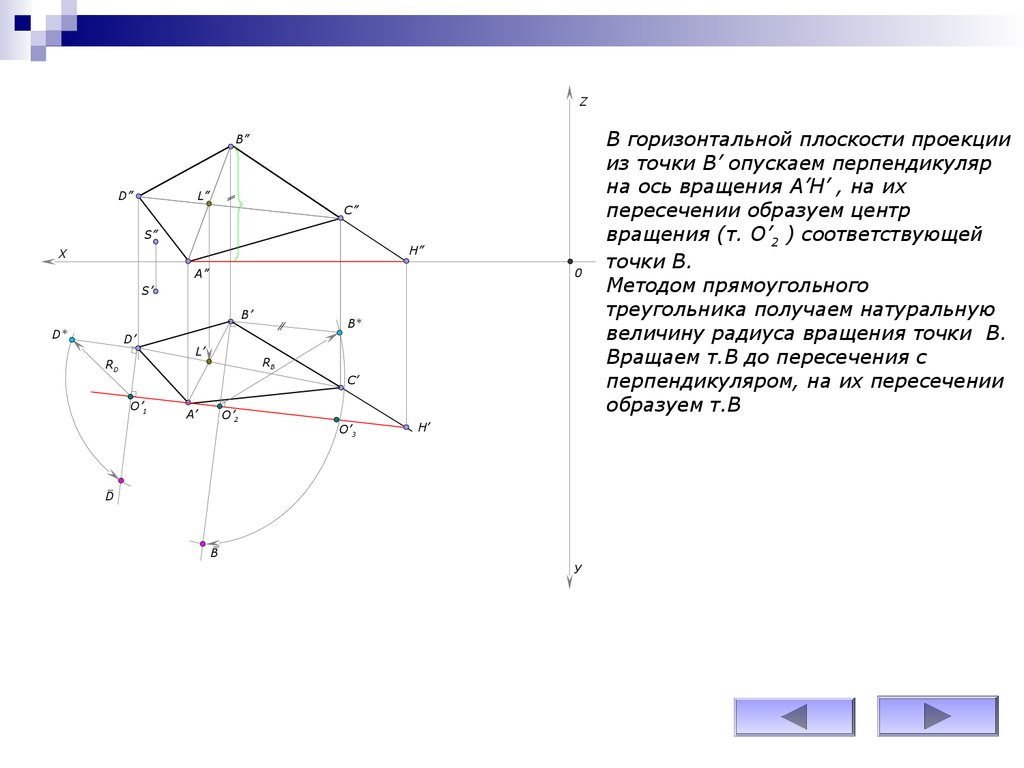
В горизонтальной плоскости проекции
из точки В’ опускаем перпендикуляр
на ось вращения A’H’ , на их
пересечении образуем центр
вращения (т. О’2 ) соответствующей
точки В.
Методом прямоугольного
треугольника получаем натуральную
величину радиуса вращения точки В.
Вращаем т.В до пересечения с
перпендикуляром, на их пересечении
образуем т.В
31.
ZB”
L”
D”
C”
S”
H”
X
0
A”
S’
B’
D*
D’
RD
L’
B*
RB
C’
O’1
C*
RC
A’
O’2
O’3
H’
C
D
B
У
В горизонтальной плоскости проекции
из точки С’ опускаем перпендикуляр на
ось вращения A’H’, на их пересечении
образуем центр вращения
(т.О’3)соответствующей точки С.
Методом прямоугольного треугольника
получаем натуральную величину
радиуса вращения точки С.
Вращаем т.C до пересечения с
перпендикуляром, на их пересечении
образуем т.С.
Точку А не вращаем, так как она лежит
на оси вращения.
32.
ZB”
L”
D”
C”
S”
H”
X
0
A”
S’
B’
D*
D’
RD
L’
B*
RB
C’
O’1
C*
RC
A’
O’2
НВ
D
B
O’3
H’
C
У
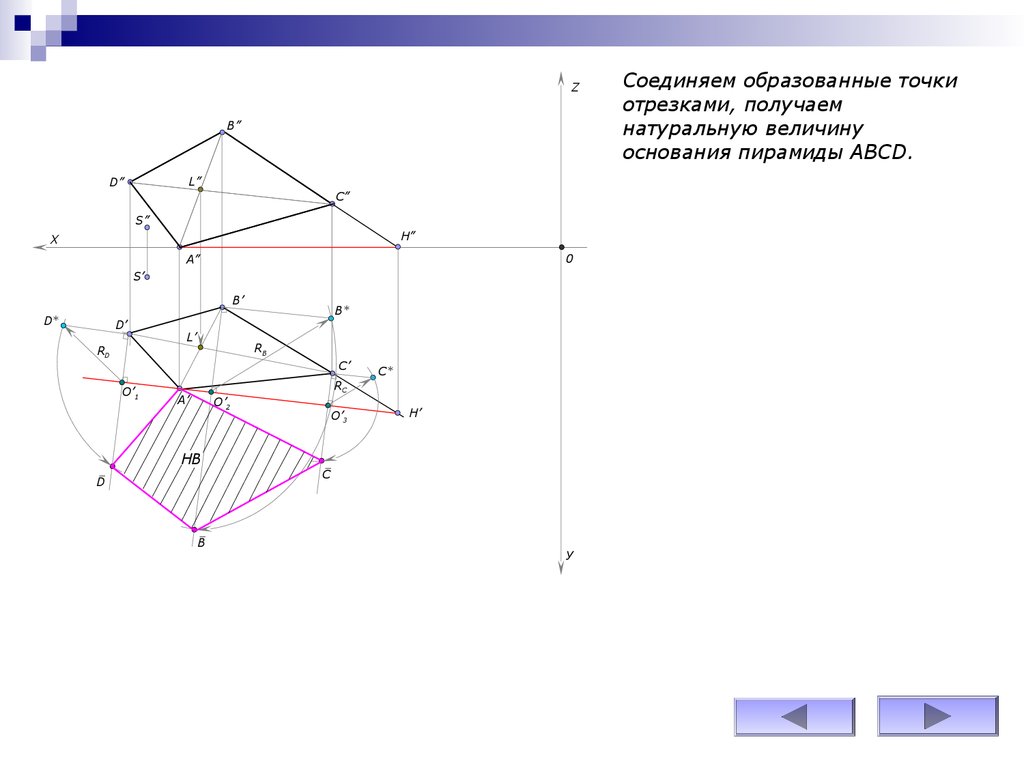
Соединяем образованные точки
отрезками, получаем
натуральную величину
основания пирамиды АВСD.
33.
ZB”
L”
D”
C”
S”
A” H”
H”
X
0
A”
S’
B’
D*
D’
R1
RB
R2
C’
A’
O’2
R3
RC
O’3
RC
RC
C*
H’
B’
НВ
D
B
RC
C’
RB
L’
RB
O’1
B*
C
RB
A’ H’
У
Приводим плоскость АВС в
положение проецирующей
плоскости, т.е. перпендикулярной
плоскости проекции. Для получения
фронтально-проецирующей
плоскости необходимо горизонталь
АH плоскости вместе с системой
всех точек плоскости ( АВС)
поставить в положение,
перпендикулярное фронтальной
плоскости проекций.
34.
ZПереносим т.S – вершину пирамиды.
B”
L”
D”
C”
S”
A” H”
H”
X
0
A”
S’
B’
D*
D’ RS
R1
O’1
B*
RS
L’
A’
R2
RS
C’
C’
RS
C*
R3
O’2
O’3
H’
B’
НВ
D
C
RS
A’ H’
S’
B
У
35.
ZB”
B”
K”
L”
D”
C”
C”
S”
H”
S”
X
A” H”
0
A”
S’
B’
D*
D’
R1
L’
B*
R2
C’
O’1
A’
C’
C*
R3
O’2
O’3
H’
B’
НВ
D
C
A’ H’
S’
B
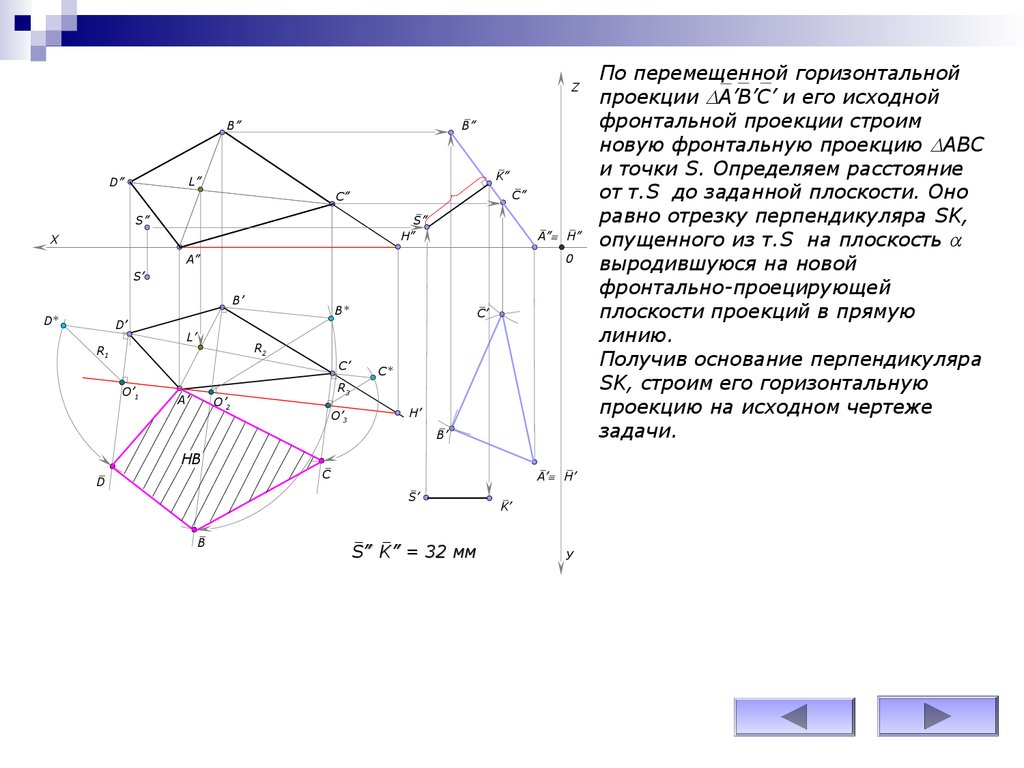
S” K” = 32 мм
K’
У
По перемещенной горизонтальной
проекции A’В’С’ и его исходной
фронтальной проекции строим
новую фронтальную проекцию АВС
и точки S. Определяем расстояние
от т.S до заданной плоскости. Оно
равно отрезку перпендикуляра SK,
опущенного из т.S на плоскость
выродившуюся на новой
фронтально-проецирующей
плоскости проекций в прямую
линию.
Получив основание перпендикуляра
SK, строим его горизонтальную
проекцию на исходном чертеже
задачи.
36.
ZB”
B”
K”
L”
D”
C”
Двугранный угол измеряется
линейным углом, составленным
линиями пересечения граней
двугранного угла с плоскостью,
перпендикулярной к его ребру.
C”
S”
H”
S”
X
A” H”
0
A”
S’
B’
D*
D’
RD
L’
B*
B”
RB
C’
O’1
C’
C*
RC
A’
O’2
O’3
H’
B’
НВ
D
X
C
A’ H’
S’
B
S” K” = 32 мм
C”
S”
K’
П2
П1
0
A”
S'
B’
У
C’
A’
37.
ZB”
B”
K”
L”
D”
C”
C”
S”
H”
S”
X
A” H”
0
A”
S’
B’
D*
D’
RD
L’
B*
BIV
RB
RC
A’
C’
SIV
C’
O’1
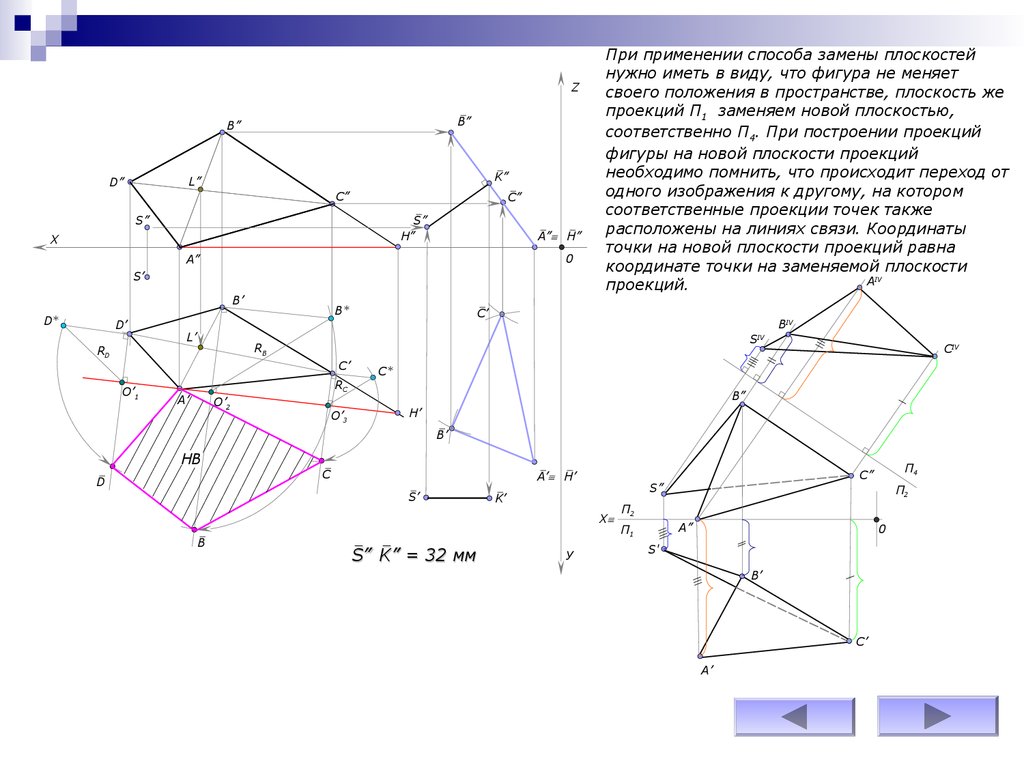
При применении способа замены плоскостей
нужно иметь в виду, что фигура не меняет
своего положения в пространстве, плоскость же
проекций П1 заменяем новой плоскостью,
соответственно П4. При построении проекций
фигуры на новой плоскости проекций
необходимо помнить, что происходит переход от
одного изображения к другому, на котором
соответственные проекции точек также
расположены на линиях связи. Координаты
точки на новой плоскости проекций равна
координате точки на заменяемой плоскости
AIV
проекций.
O’2
O’3
CIV
C*
B”
H’
B’
НВ
D
C
A’ H’
S’
K’
X
B
S” K” = 32 мм
У
П4
C”
S”
П2
П2
A”
П1
0
S'
B’
C’
A’
38.
ZB”
B”
K”
L”
D”
C”
Для того чтобы линейный угол
спроецировался на плоскость проекций в
натуральную величину, надо новую
плоскость проекций П5 поставить
перпендикулярно к ребру ВС двугранного
угла.A
V
П5 П4
C”
S”
H”
S”
X
0
A”
AIV
A” H”
SV
BV C V
S’
SIV
B’
D*
D’
RD
L’
CIV
B*
C’
B”
RB
C’
O’1
C*
=40°
RC
A’
O’2
O’3
H’
D
X
C
A’ H’
S’
B
S” K” = 32 мм
K’
П4
C”
S”
B’
НВ
BIV
П2
П2
П1
0
A”
S'
B’
У
C’
A’
меню
39.
Графическая работа №3 лист 1Пересечение поверхности плоскостью.
Цель работы: закрепление знаний и приобретение
навыков в решении позиционных задач на поверхности
и построении разверток поверхностей.
40.
Условие задачи.1.Построить проекции сечения правильной пирамиды
плоскостью общего положения заданной тремя точками
А,В,С (координаты точек смотри в приложении). Центр
окружности описанной вокруг основания пирамиды
расположен в точке К с координатами (70,60,0).
2.Построить полную развертку усеченной пирамиды по
условию предыдущей задачи.
41.
Для выполнения данной графической работы используется лист форматаА3 (290х420 мм)
42.
Оформляется рамкой, угловым штампом и заполнением основной надписи43.
44.
ZS”
B”
А”
C”
П1
D”
F”
E”
0
П2
А’
D’
У
B’
S’
F’
K’
E’
C’
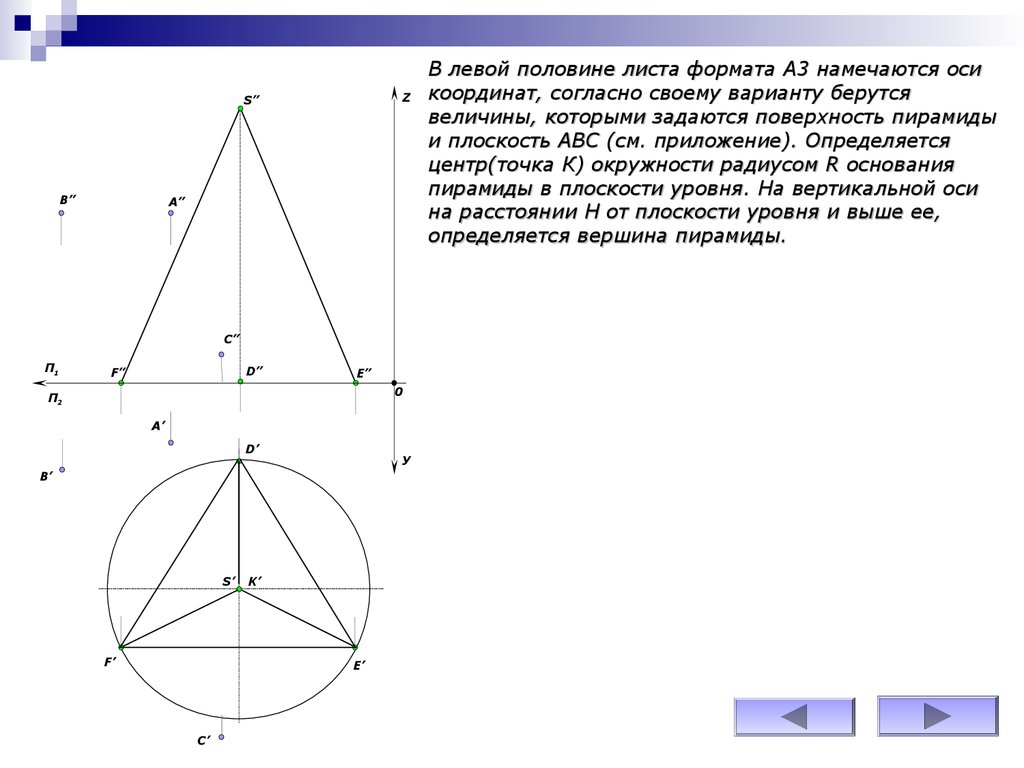
В левой половине листа формата А3 намечаются оси
координат, согласно своему варианту берутся
величины, которыми задаются поверхность пирамиды
и плоскость АВС (см. приложение). Определяется
центр(точка К) окружности радиусом R основания
пирамиды в плоскости уровня. На вертикальной оси
на расстоянии Н от плоскости уровня и выше ее,
определяется вершина пирамиды.
45.
ZS”
B”
А”
C”
П1
D”
F”
E”
0
П2
А’
D’
У
B’
S’
F’
K’
E’
C’
По координатам точек А, В, С определяется
секущая плоскость.
46.
ZS”
B”
А”
В целях облегчения построения линии сечения
строится дополнительный чертеж заданных
геометрических образов.
Выбирается дополнительная система П1/П4 плоскостей
проекций с таким расчетом, чтобы секущая плоскость
была представлена как проецирующая.
Дополнительная плоскость проекций П4
перпендикулярна заданной плоскости АВС.
AIV BIV
П1
C”
П1
D”
F”
П4
E”
0
П2
DIV
А’
SIV
D’
У
B’
KIV
FIV
S’
F’
K’
EIV
E’
C’
CIV
47.
ZS”
B”
А”
Линия сечения проецируется на плоскость
проекции П4 в виде отрезка прямой на следе
этой плоскости. Имея проекцию сечения на
дополнительной плоскости П4 строят основные
ее проекции.
L”
N”
C”
П1
D”
F”
П1
M”
AIV BIV
П4
E”
0
П2
DIV
LIV
А’
D’
SIV
У
B’
L’
NIV
KIV
FIV
S’
N’
MIV
K’
E
IV
M’
F’
E’
C’
CIV
48.
ZS”
B”
А”
L”
L”
N”
N”
M
C”
П1
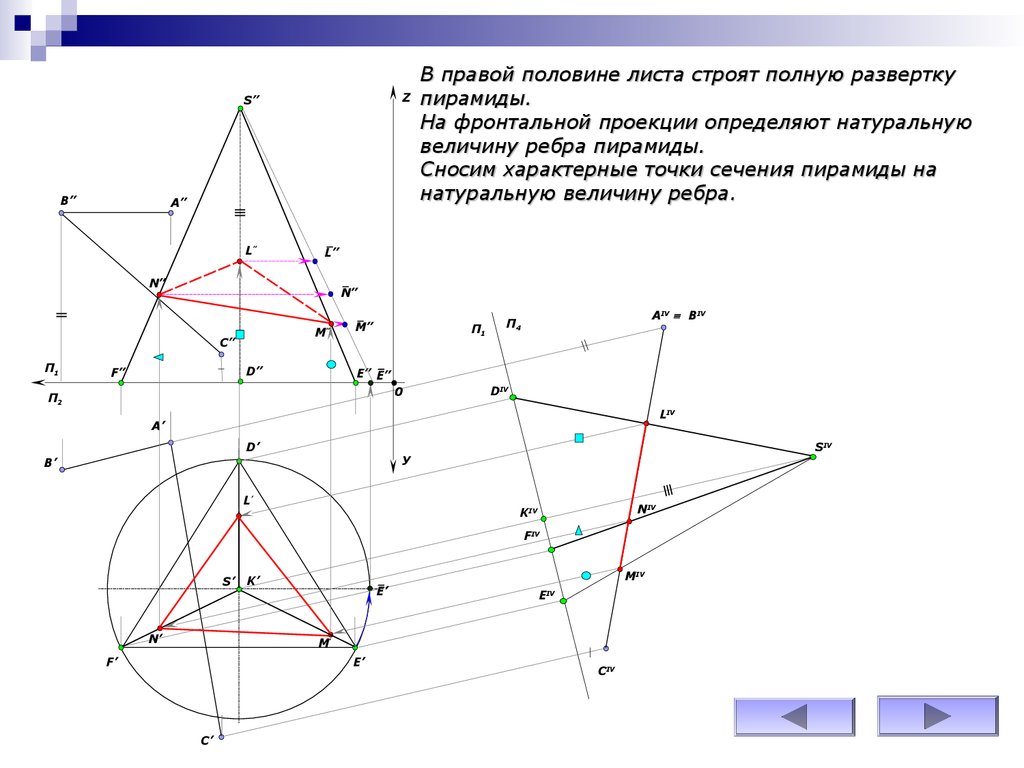
В правой половине листа строят полную развертку
пирамиды.
На фронтальной проекции определяют натуральную
величину ребра пирамиды.
Сносим характерные точки сечения пирамиды на
натуральную величину ребра.
”
D”
F”
M”
П1
AIV BIV
П4
E” E”
0
П2
DIV
LIV
А’
D’
SIV
У
B’
L’
NIV
KIV
FIV
S’
N’
MIV
K’
E’
E
IV
M’
F’
E’
C’
CIV
49.
SR1
R1
Z
S”
R1
D
D
R1
B”
А”
R
R1
R
L
”
L”
N”
M”
C”
П1
F
N”
D”
F”
M”
П1
A
BIV
П4
R
E” E”
0
П2
E
R
IV
R
DIV
LIV
А’
D’
У
B’
L’
SIV
NIV
KIV
R
FIV
M
S’ K’
N’
EIV
M’
F’
E’
CI
V
C’
IV
D
Зная натуральную величину ребра
пирамиды, строят ее развертку.
50.
SRL
RL
L
Z
S”
L
RN
RM
D
B”
А”
RN
L
”
RL
N
RM
П1
M
L”
N”
F
N”
M”
C”
D”
F”
D
M”
П1
A
П4
IV
B
E
IV
E” E”
0
П2
DIV
LIV
А’
D’
У
B’
L’
SIV
NIV
KIV
FIV
MIV
S’ K’
N’
E
IV
M’
F’
E’
CI
V
C’
D
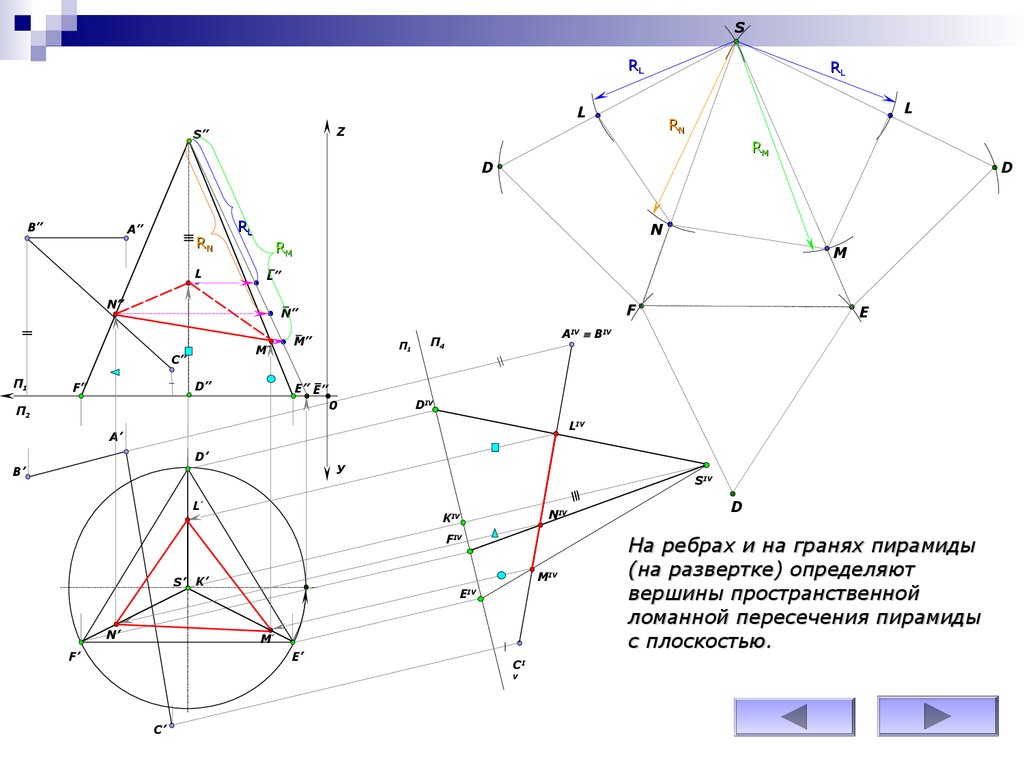
На ребрах и на гранях пирамиды
(на развертке) определяют
вершины пространственной
ломанной пересечения пирамиды
с плоскостью.
51.
SM
L
L
Z
S”
R1
D
B”
D
R
R1
N
А”
R
L
”
L”
N”
П1
F
N”
M”
C”
D”
F”
M
M”
П1
E
A
BIV
IV
П4
E” E”
0
П2
DIV
LIV
А’
D’
У
B’
L’
SIV
NIV
KIV
D
FIV
MIV
S’ K’
N’
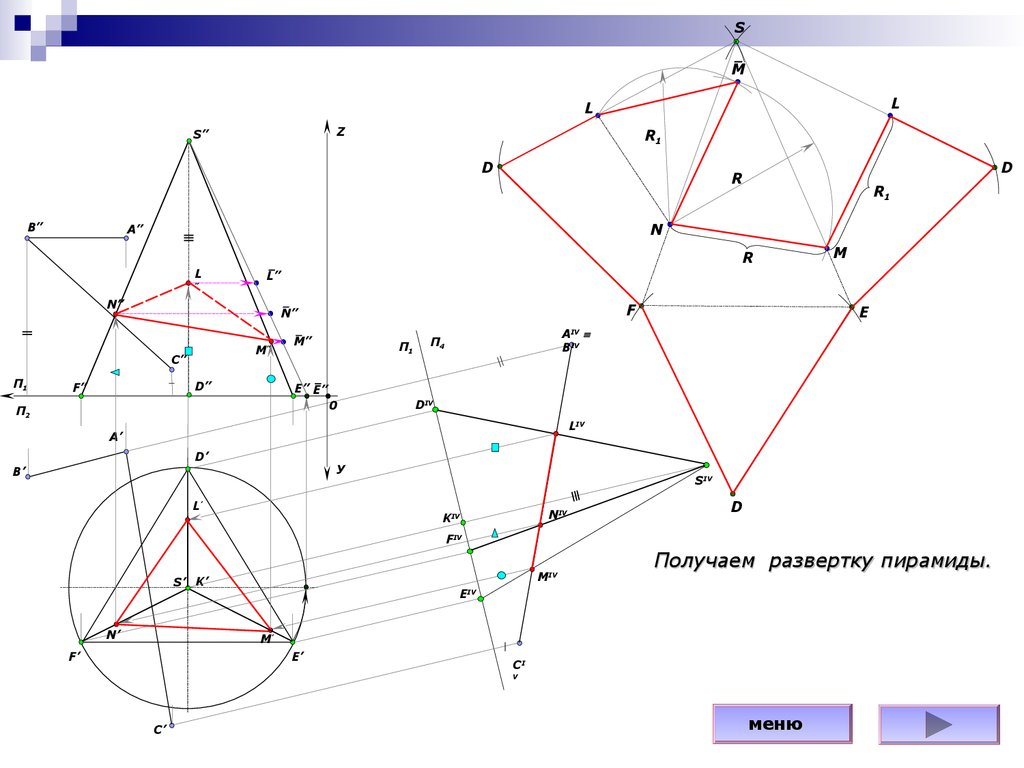
Получаем развертку пирамиды.
EIV
M’
F’
E’
CI
V
C’
меню
52. Графическая работа №3 лист 2
Взаимное пересечение поверхностей.Развертка конуса.
Цель работы: закрепление знаний и приобретение
навыков в решении позиционных задач на поверхности и
построение разверток поверхностей
53.
Условие задачи.1) построить проекции линии пересечения двух
поверхностей способом вспомогательных
секущих плоскостей.
2) построить проекции линии пересечения двух
поверхностей способом концентрических сфер.
3) построить развертку боковой поверхности
конуса с нанесением линии пересечения по
условию задачи 1 или 2.
54.
Для выполнения данной графической работы используется листформата А3 (290х420 мм)
55.
Оформляется рамкой, угловым штампом и заполнением основной надписи.56.
57.
K”S”
К’
S’
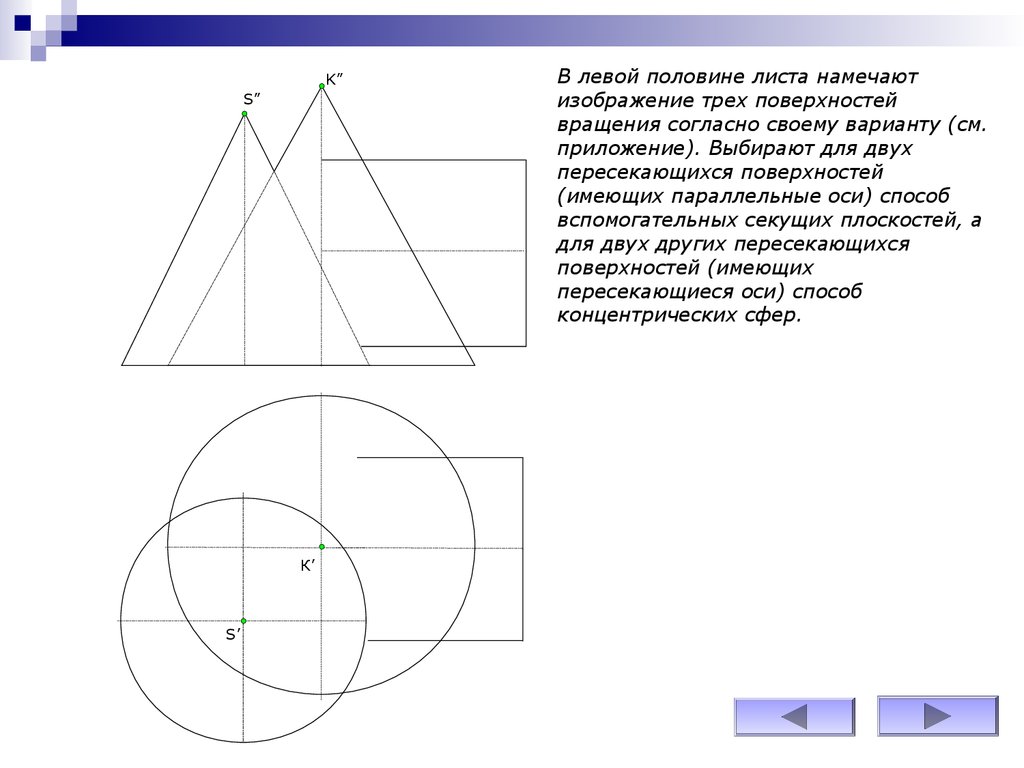
В левой половине листа намечают
изображение трех поверхностей
вращения согласно своему варианту (см.
приложение). Выбирают для двух
пересекающихся поверхностей
(имеющих параллельные оси) способ
вспомогательных секущих плоскостей, а
для двух других пересекающихся
поверхностей (имеющих
пересекающиеся оси) способ
концентрических сфер.
58.
При решении задачи с помощьювспомогательных секущих плоскостей
определяют точки линии пересечения
поверхностей.
Начинают построения с характерных
краевых точек линии пересечения.
K”
S”
S”
3”
2”
1”
’
1’
K’
S’
3’
S’
2’
’
59.
K”S”
S”
3”
1”
4”
5”
R 1’
R1
1”
2”
1’
R 1’
’
S’
K’
5’
3’
R1
S’
4’
2’
’
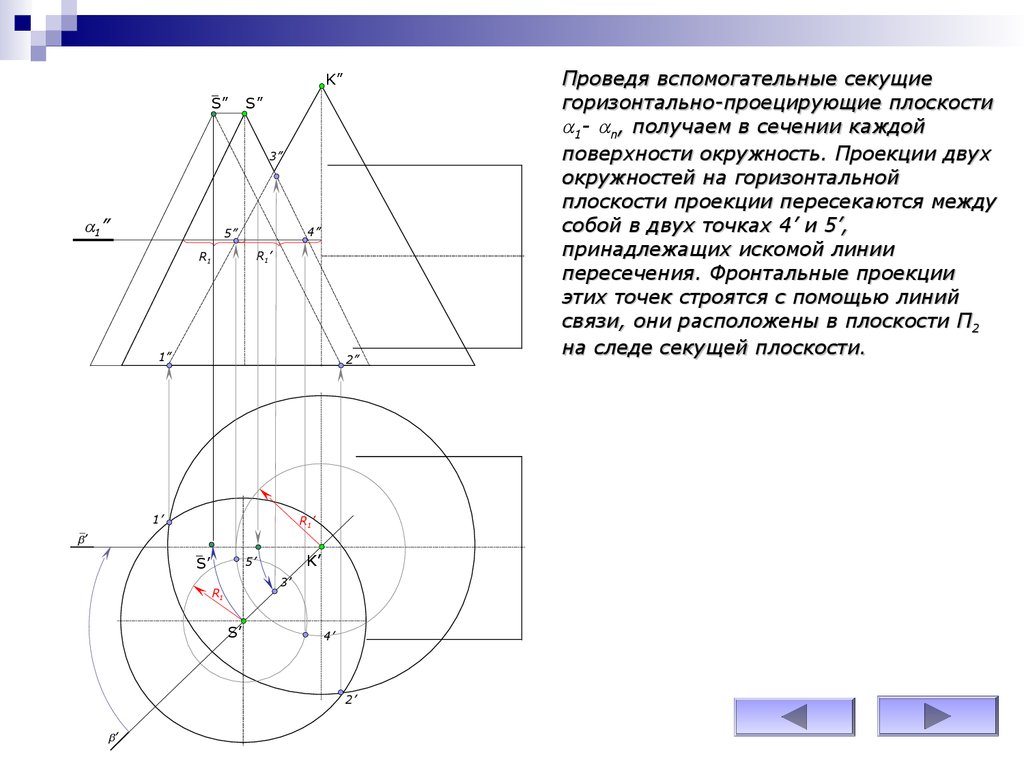
Проведя вспомогательные секущие
горизонтально-проецирующие плоскости
1- n, получаем в сечении каждой
поверхности окружность. Проекции двух
окружностей на горизонтальной
плоскости проекции пересекаются между
собой в двух точках 4’ и 5’,
принадлежащих искомой линии
пересечения. Фронтальные проекции
этих точек строятся с помощью линий
связи, они расположены в плоскости П2
на следе секущей плоскости.
60.
K”S”
S”
3”
1”
4”
5”
R1
2”
R 1’
7”
6”
R2
R 2’
1”
2”
R2 ’
R1 ’
1’
7’
’
5’
S’
K’
3’
R2
R1
S’
4’
6’
2’
’
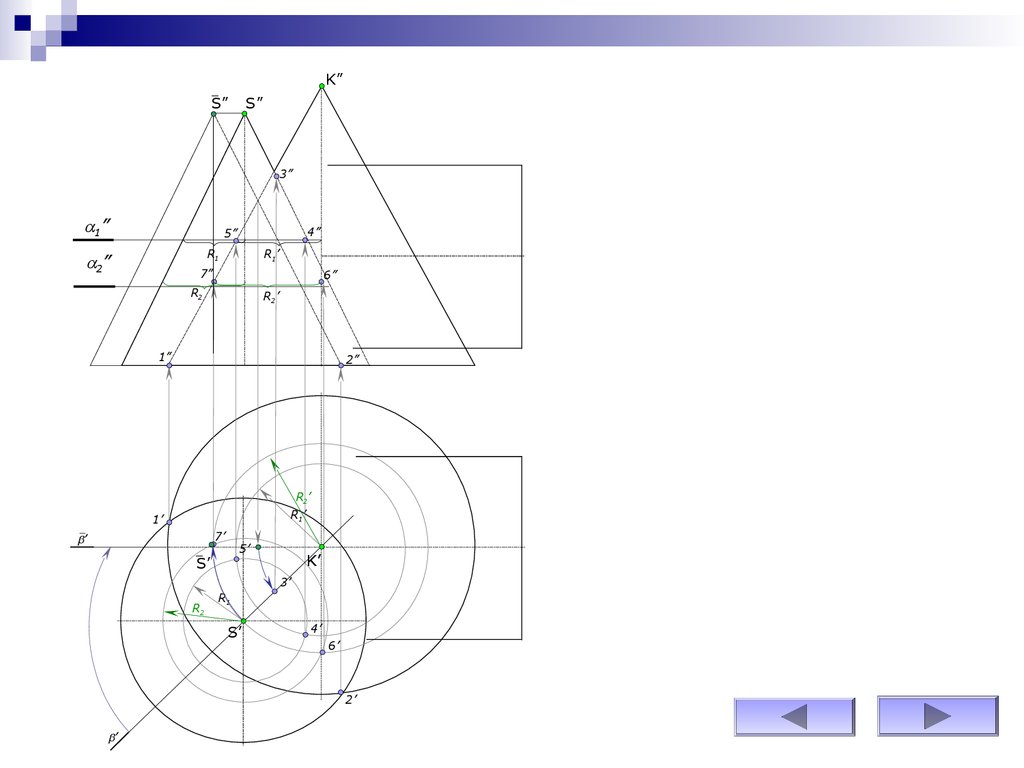
61.
K”S”
S”
3”
1”
4”
5”
R1
2”
R 1’
7”
6”
R2
3”
R 2’
9”
8”
R 3’
R3
1”
2”
R3 ’
R2 ’
9’
1’
’
R1 ’
7’
5’
S’
K’
3’
R2
R1
S’
R3
4’
6’
8’
2’
’
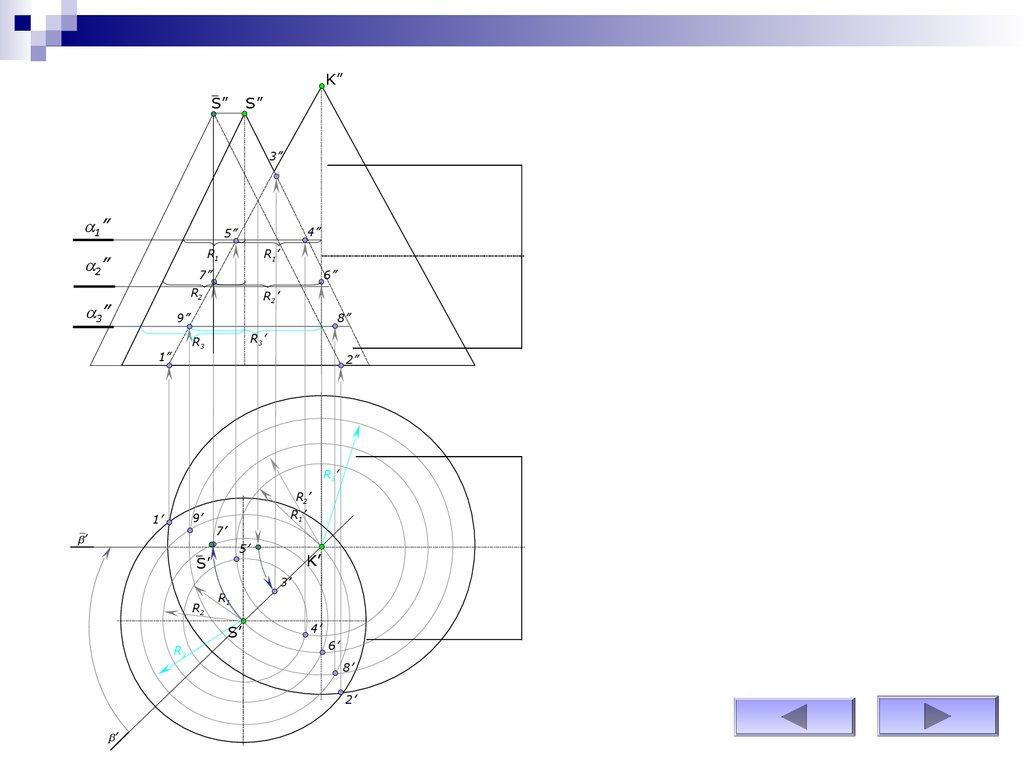
62.
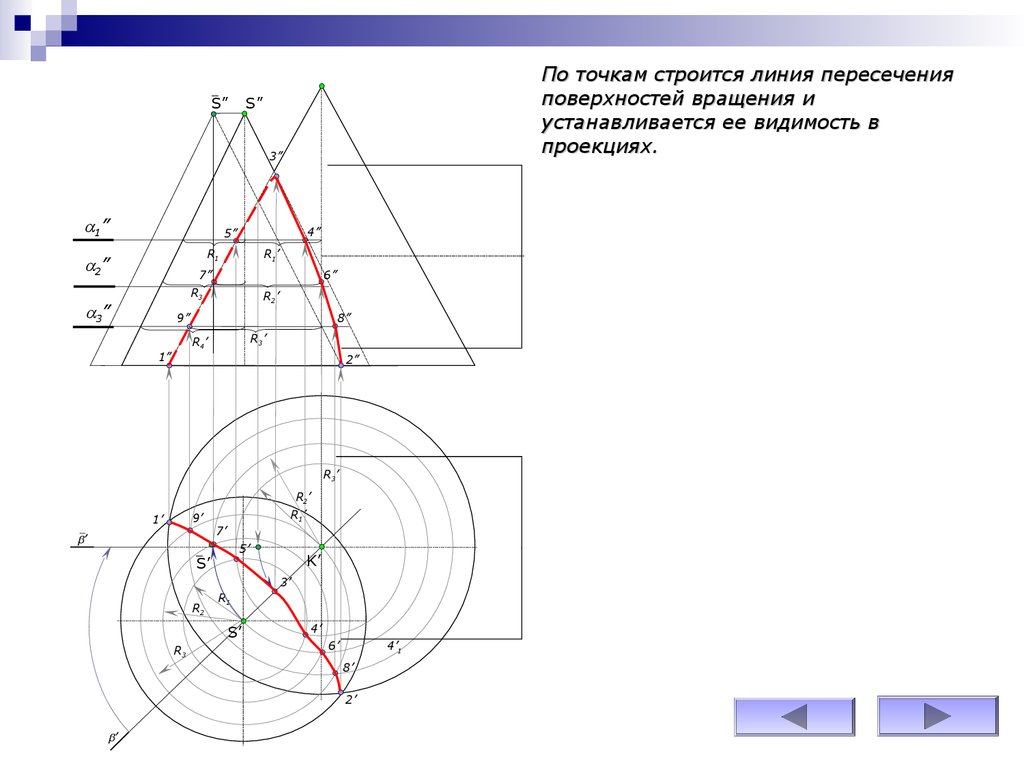
По точкам строится линия пересеченияповерхностей вращения и
устанавливается ее видимость в
проекциях.
S”
S”
3”
1”
4”
5”
R1
2”
R 1’
7”
6”
R3
3”
R 2’
9”
8”
R 3’
R4 ’
1”
2”
R3 ’
R2 ’
9’
1’
’
R1 ’
7’
5’
S’
K’
3’
R2
R1
S’
R3
4’
6’
4’1
8’
2’
’
63.
S”S”
3”
1”
1”
4”
5”
R1
2”
R 1’
7”
6”
R3
3”
R 2’
9”
8”
R 3’
R4 ’
1”
2”
2”
R3 ’
R2 ’
9’
1’
’
R1 ’
7’
1’
5’
S’
K’
3’
R2
R1
S’
R3
4’
6’
8’
2’
’
2’
При решении задачи с помощью
вспомогательных концентрических сфер
необходимо выполнение следующих
условий:
•обе поверхности должны быть
поверхностями вращения;
•их оси должны пересекаться;
•каждая ось должна быть параллельна
какой-либо плоскости проекций.
Построение начинаем с определения
характерных краевых точек 1 и 2 линии
пересечения поверхностей.
64.
S”S”
3”
1”
1”
R1
7”
6”
R 2’
9”
8”
R 3’
R4 ’
1”
R1
R 1’
R3
3”
3” 3”1
4”
5”
2”
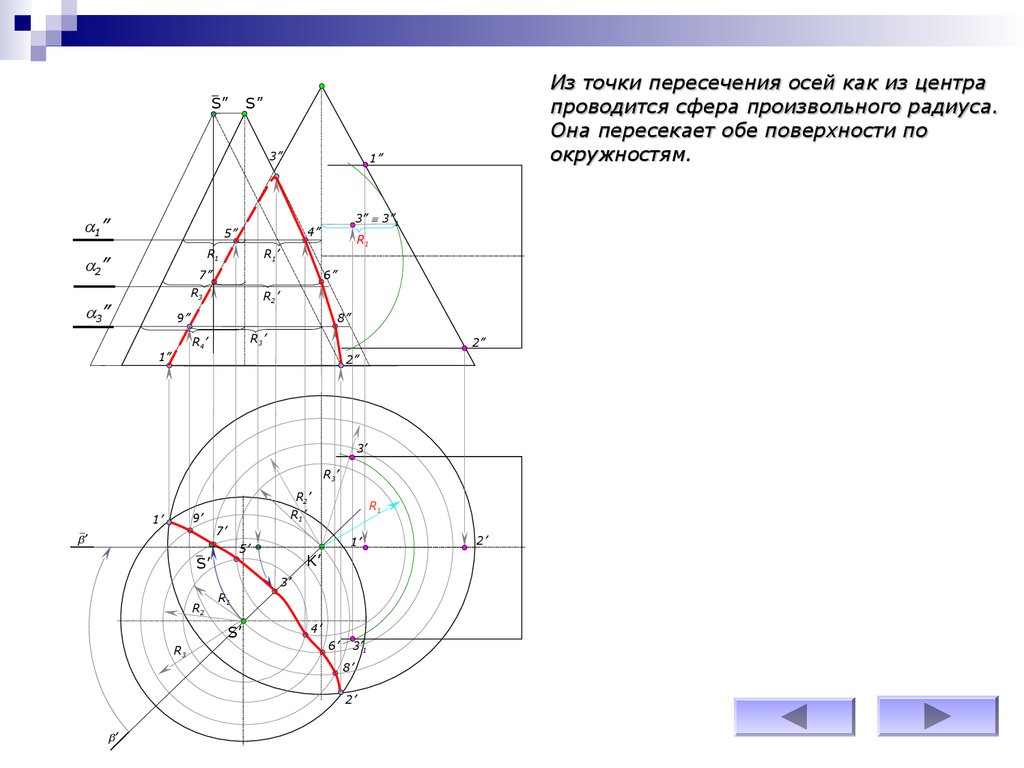
Из точки пересечения осей как из центра
проводится сфера произвольного радиуса.
Она пересекает обе поверхности по
окружностям.
2”
2”
3’
R3 ’
R2 ’
9’
1’
’
R1
R1 ’
7’
1’
5’
S’
K’
3’
R2
R1
S’
R3
4’
6’
3’1
8’
2’
’
2’
65.
S”S”
3”
1”
1”
R1
7”
4” 4”1
6”
R 2’
R2
9”
8”
R 3’
R4 ’
1”
R1
R 1’
R3
3”
3” 3”1
4”
5”
2”
Изменяя радиус вспомогательной секущей
сферы, можно получить
последовательный ряд точек линии
пересечения.
2”
2”
3’
4’
R3 ’
R2 ’
9’
1’
’
R1
R1 ’
7’
1’
5’
S’
K’
2’
R2
3’
R2
R1
S’
R3
4’
6’
3’1
8’
2’
’
4’1
66.
S”S”
3”
1”
1”
R1
2”
7”
4” 4”1
6”
R 2’
R2
9”
8”
5” 5”1
R3
R 3’
R4 ’
1”
R1
R 1’
R3
3”
3” 3”1
4”
5”
2”
2”
3’
4’
5’
R3 ’
R2 ’
9’
1’
’
R1
R1 ’
7’
1’
5’
S’
K’
3’
R2
R3
R3
R1
S’
5’1
4’
6’
3’1
8’
2’
’
2’
R2
4’1
67.
S”S”
3”
1”
1”
R1
7”
4” 4”1
6”
R 2’
R2
9”
8”
5” 5”1
R3
R 3’
R4 ’
1”
R1
R 1’
R3
3”
3” 3”1
4”
5”
2”
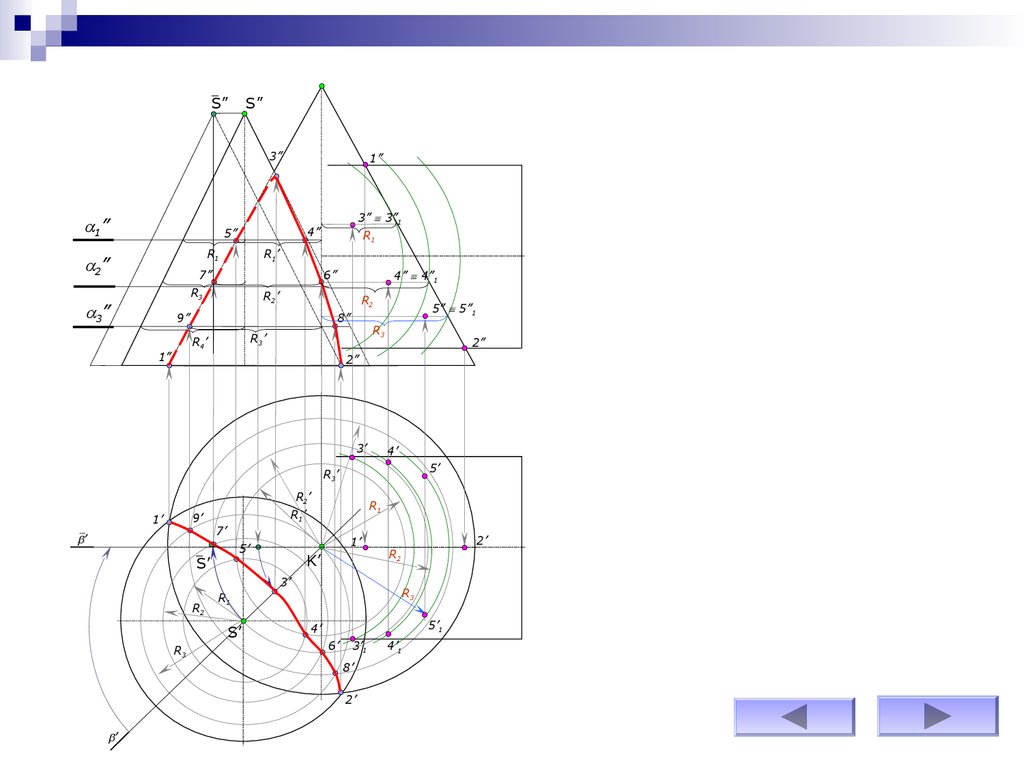
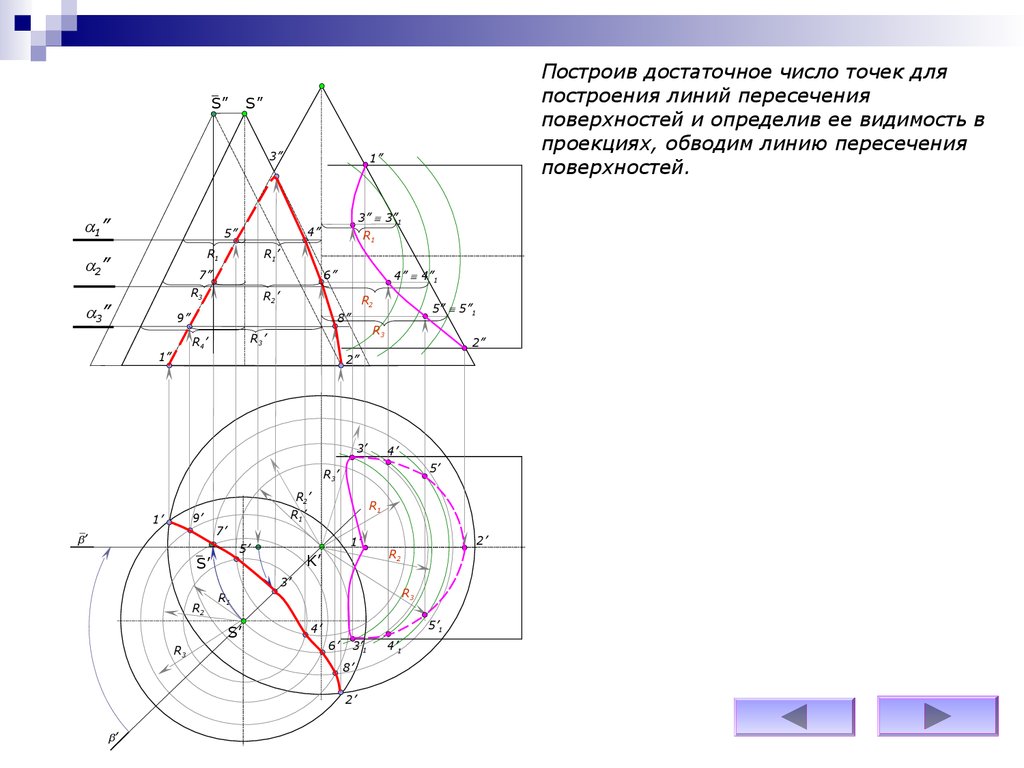
Построив достаточное число точек для
построения линий пересечения
поверхностей и определив ее видимость в
проекциях, обводим линию пересечения
поверхностей.
2”
2”
3’
4’
5’
R3 ’
R2 ’
9’
1’
’
R1
R1 ’
7’
1’
5’
S’
K’
3’
R2
R3
R3
R1
S’
5’1
4’
6’
3’1
8’
2’
’
2’
R2
4’1
68.
S”S”
3”
1”
1”
R1
7”
4” 4”1
6”
R 2’
R2
9”
8”
5” 5”1
R3
R 3’
R4 ’
1”
R1
R 1’
R3
3”
3” 3”1
4”
5”
2”
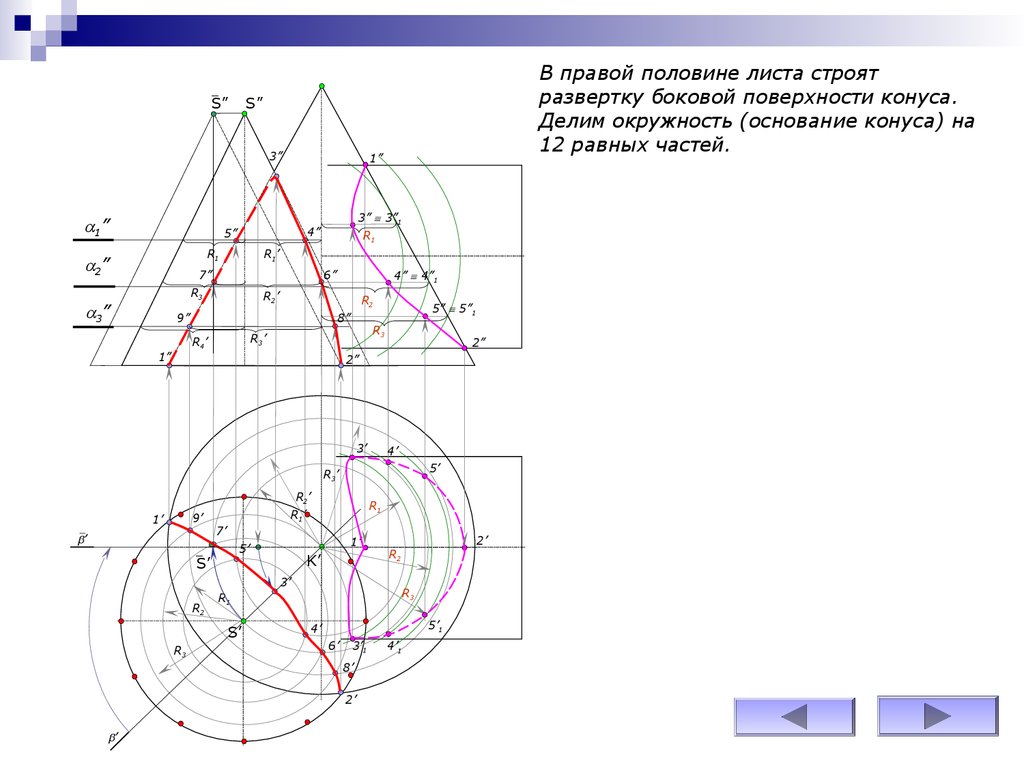
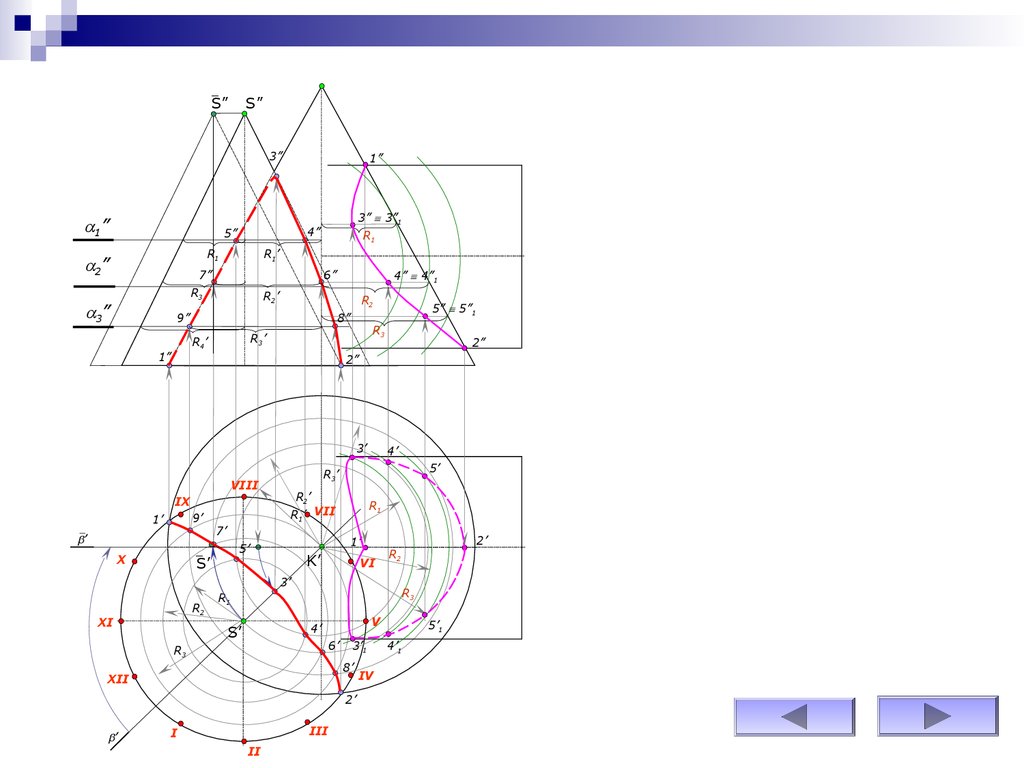
В правой половине листа строят
развертку боковой поверхности конуса.
Делим окружность (основание конуса) на
12 равных частей.
2”
2”
3’
4’
5’
R3 ’
R2 ’
9’
1’
’
R1
R1 ’
7’
1’
5’
S’
K’
3’
R2
R3
R3
R1
S’
5’1
4’
6’
3’1
8’
2’
’
2’
R2
4’1
69.
S”S”
3”
1”
R1
R1
R 1’
7”
R 2’
R2
9”
8”
2”
2”
3’
1’
’
X
7’
R1
2’
1’
5’
S’
5’
R2 ’
R1’ VII
IX
9’
4’
R3 ’
VIII
K’
VI
3’
R2
XI
V
4’
S’
6’
3’1
8’
XII
2’
III
I
II
R2
R3
R1
R3
’
5” 5”1
R3
R 3’
R4 ’
1”
4” 4”1
6”
R3
3”
3” 3”1
4”
5”
2”
1”
IV
5’1
4’1
70.
S”S”
3”
1”
L
1”
2”
3” 3”1
4”
5”
7”
R1
4” 4”1
6”
R2
3”
9”
8”
1”
5” 5”1
R3
2”
2”
S
3’
R2 ’
R1’ VII
’
X
7’
2’
1’
5’
S’
R1
K’
VI
3’
R2
XI
R3
R1
V
4’
S’
6’
R3
3’1
8’
XII
2’
’
III
I
II
R2
IV
5’1
4’1
L
IX
1’
5’
R3 ’
VIII
9’
4’
71.
S”S”
II
III
3”
1”
7”
R1
V
4” 4”1
6”
R2
3”
I
VI
3” 3”1
4”
5”
2”
1”
9”
8”
1”
5” 5”1
R3
IV
2”
2”
S
VII
3’
’
X
7’
K’
VI
3’
R2
XI
V
4’
6’
R3
3’1
8’
XII
2’
’
III
I
II
R2
R3
R1
S’
VIII
2’
1’
5’
S’
R1
L
R2 ’
R1’ VII
IX
1’
5’
R3 ’
VIII
9’
4’
IV
IX
5’1
4’1
X
I
XI
XII
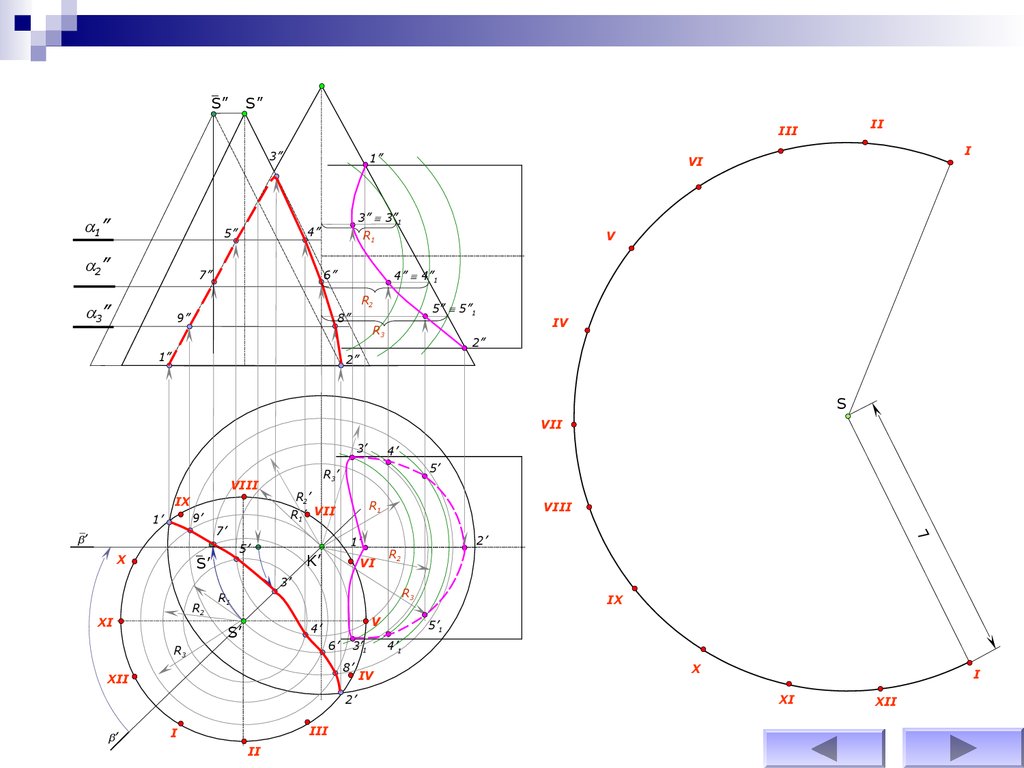
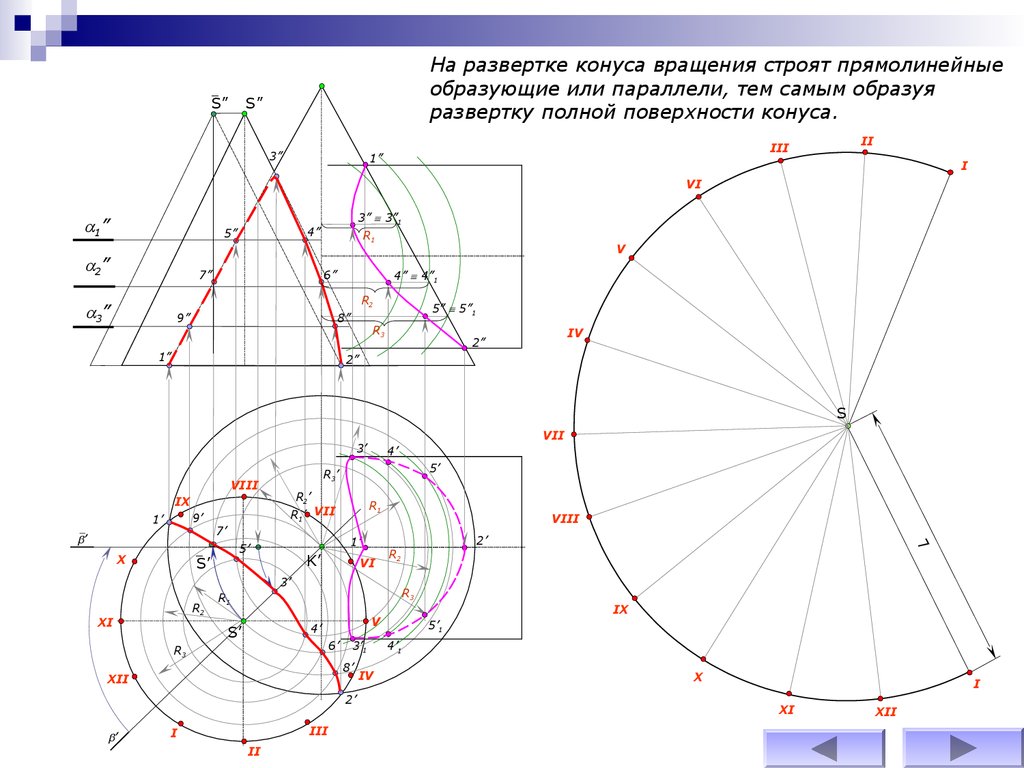
72.
На развертке конуса вращения строят прямолинейныеобразующие или параллели, тем самым образуя
развертку полной поверхности конуса.
S”
S”
3”
II
III
1”
I
VI
1”
2”
3” 3”1
4”
5”
7”
R1
V
4” 4”1
6”
R2
3”
9”
8”
1”
5” 5”1
R3
IV
2”
2”
S
VII
3’
’
X
7’
K’
VI
3’
R2
XI
6’
3’1
8’
XII
2’
III
I
II
IX
V
4’
R3
’
R2
R3
R1
S’
VIII
2’
1’
5’
S’
R1
L
R2 ’
R1’ VII
IX
1’
5’
R3 ’
VIII
9’
4’
IV
5’1
4’1
X
I
XI
XII
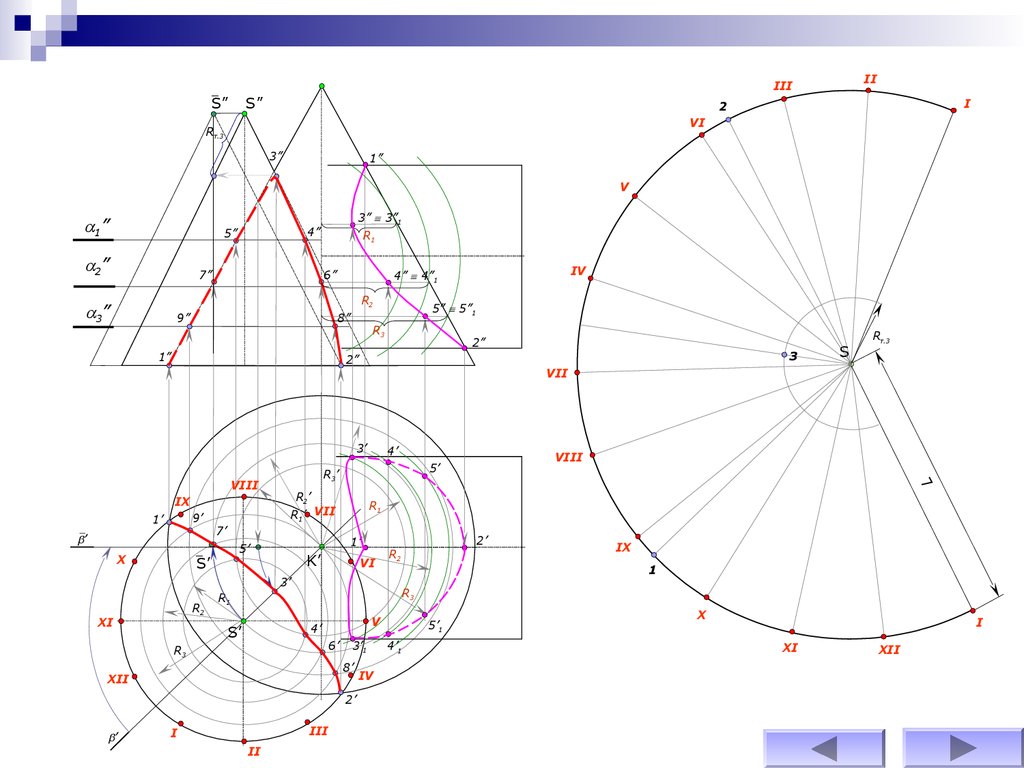
73.
Далее проводят образующие, проходящие черезхарактерные точки линий пересечения конуса вращения с
поверхностью вращения.
S”
S”
3”
II
III
1”
I
2
VI
1”
2”
3” 3”1
4”
5”
7”
R1
V
4” 4”1
6”
R2
3”
9”
8”
1”
5” 5”1
R3
IV
2”
2”
S
VII
3’
’
X
7’
K’
VI
3’
R2
XI
6’
3’1
8’
XII
2’
III
I
II
IX
V
4’
R3
’
R2
R3
R1
S’
VIII
2’
1’
5’
S’
R1
L
R2 ’
R1’ VII
IX
1’
5’
R3 ’
VIII
9’
4’
IV
5’1
1
4’1
X
I
XI
XII
74.
IIIII
S”
S”
I
2
VI
Rт.3
3”
1”
V
1”
2”
3” 3”1
4”
5”
7”
R1
R2
3”
9”
8”
1”
5” 5”1
R3
2”
2”
1’
’
X
S’
R1
2’
1’
5’
K’
VI
3’
R2
XI
6’
R3
3’1
8’
XII
2’
III
II
IX
1
V
4’
I
R2
R3
R1
S’
VIII
5’
R2 ’
R1’ VII
7’
Rт.3
L
VIII
9’
4’
R3 ’
IX
3
S
VII
3’
’
IV
4” 4”1
6”
IV
5’1
4’1
X
I
XI
XII
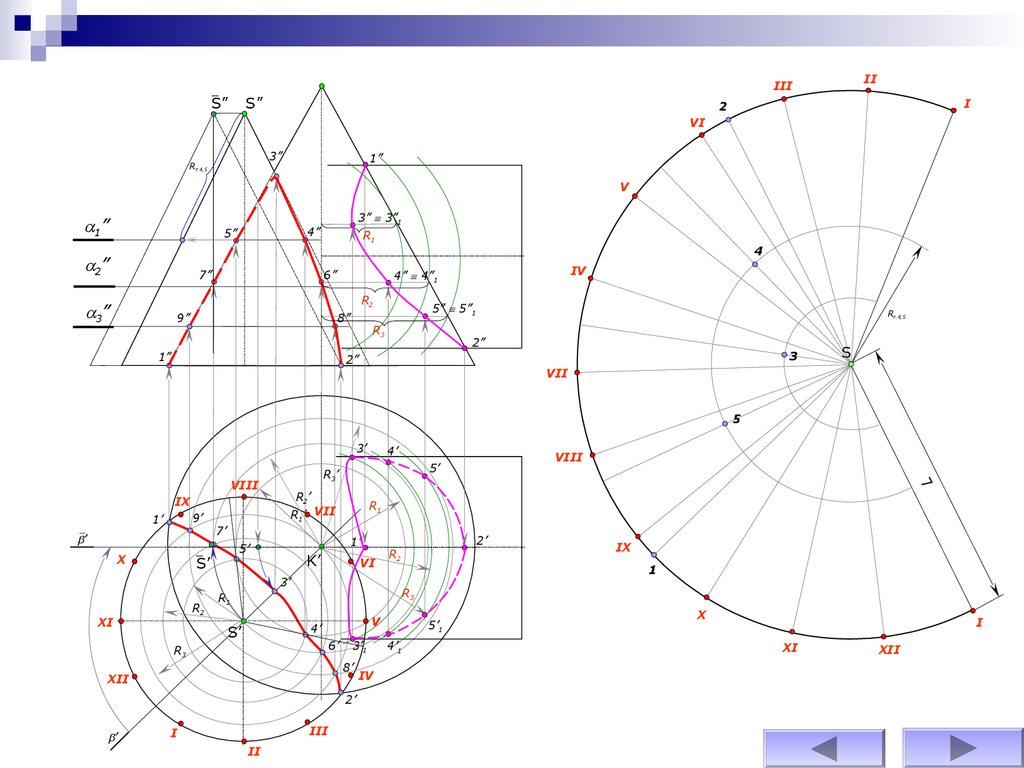
75.
IIIII
S”
S”
I
2
VI
3”
Rт.4,5
1”
V
1”
2”
3” 3”1
4”
5”
7”
R1
4
R2
3”
9”
IV
4” 4”1
6”
8”
1”
5” 5”1
R3
Rт.4,5
2”
2”
3
S
VII
5
3’
1’
’
X
R2 ’
R1’ VII
7’
R1
2’
1’
5’
S’
L
VIII
K’
VI
3’
R2
XI
6’
3’1
8’
XII
2’
III
I
II
IX
1
V
4’
R3
’
R2
R3
R1
S’
VIII
5’
R3 ’
IX
9’
4’
IV
5’1
4’1
X
I
XI
XII
76.
IIIII
S”
S”
I
2
VI
3”
1”
Rт.6,7
V
1”
4”
5”
6
3” 3”1
R1
4
2”
7”
4” 4”1
6”
R2
3”
9”
IV
8”
1”
Rт.6,7
5” 5”1
R3
2”
2”
3
S
VII
5
R2 ’
R1’ VII
IX
1’
’
X
7’
S’
2’
K’
VI
3’
R2
XI
6’
3’1
8’
XII
2’
III
I
II
IX
1
V
4’
R3
’
R2
R3
R1
S’
7
R1
1’
5’
VIII
5’
R3 ’
VIII
9’
4’
L
3’
IV
5’1
4’1
X
I
XI
XII
77.
IIIII
S”
S”
I
2
VI
3”
1”
8
V
Rт.8,9
1”
4”
5”
6
3” 3”1
R1
4
2”
7”
4” 4”1
6”
R2
3”
9”
IV
8”
1”
Rт.8,9
5” 5”1
R3
2”
2”
3
S
VII
5
R2 ’
R1’ VII
IX
1’
’
X
7’
S’
K’
XI
VI
6’
3’1
8’
XII
2’
III
I
II
IX
1
V
4’
R3
’
R2
R3
R1
S’
9
2’
3’
R2
7
R1
1’
5’
VIII
5’
R3 ’
VIII
9’
4’
L
3’
IV
5’1
4’1
X
I
XI
XII
78.
IIIII
S”
S”
I
2
VI
3”
1”
8
V
Rт.8,9
1”
4”
5”
6
3” 3”1
R1
4
2”
7”
4” 4”1
6”
R2
3”
9”
IV
8”
1”
Rт.8,9
5” 5”1
R3
2”
2”
3
S
VII
5
R2 ’
R1’ VII
IX
1’
’
X
7’
S’
K’
XI
VI
R2
IX
1
R3
R1
V
4’
S’
9
2’
3’
R2
7
R1
1’
5’
VIII
5’
R3 ’
VIII
9’
4’
L
3’
6’
R3
3’1
8’
XII
5’1
4’1
X
I
XI
IV
2’
’
III
I
II
меню
XII
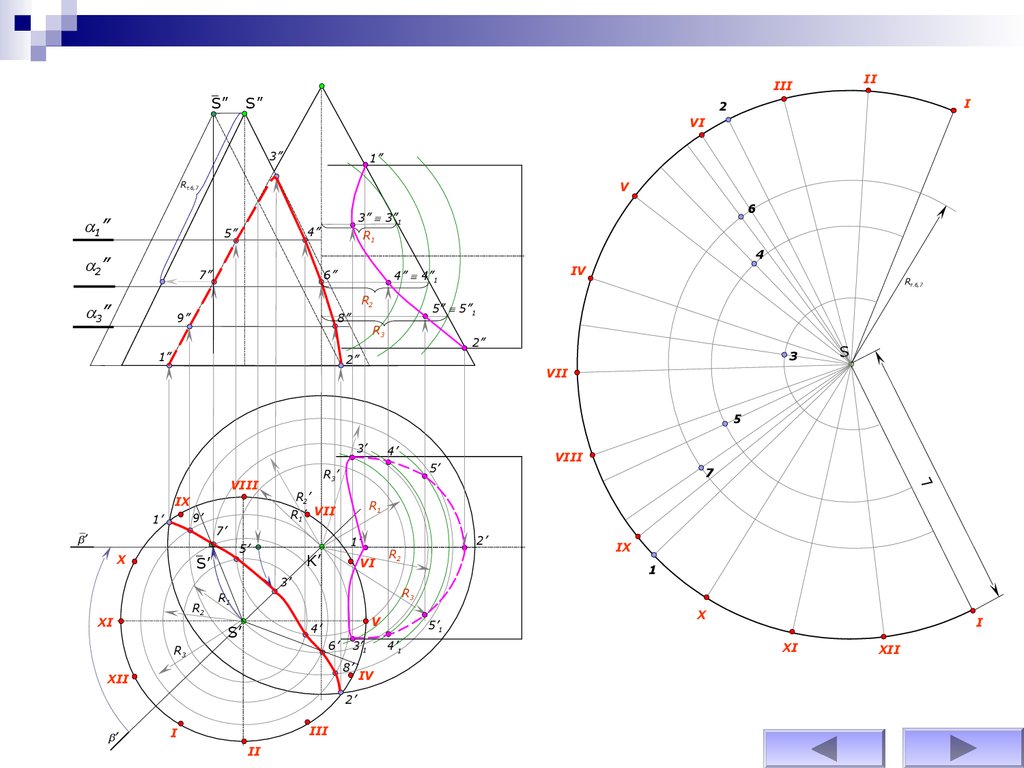
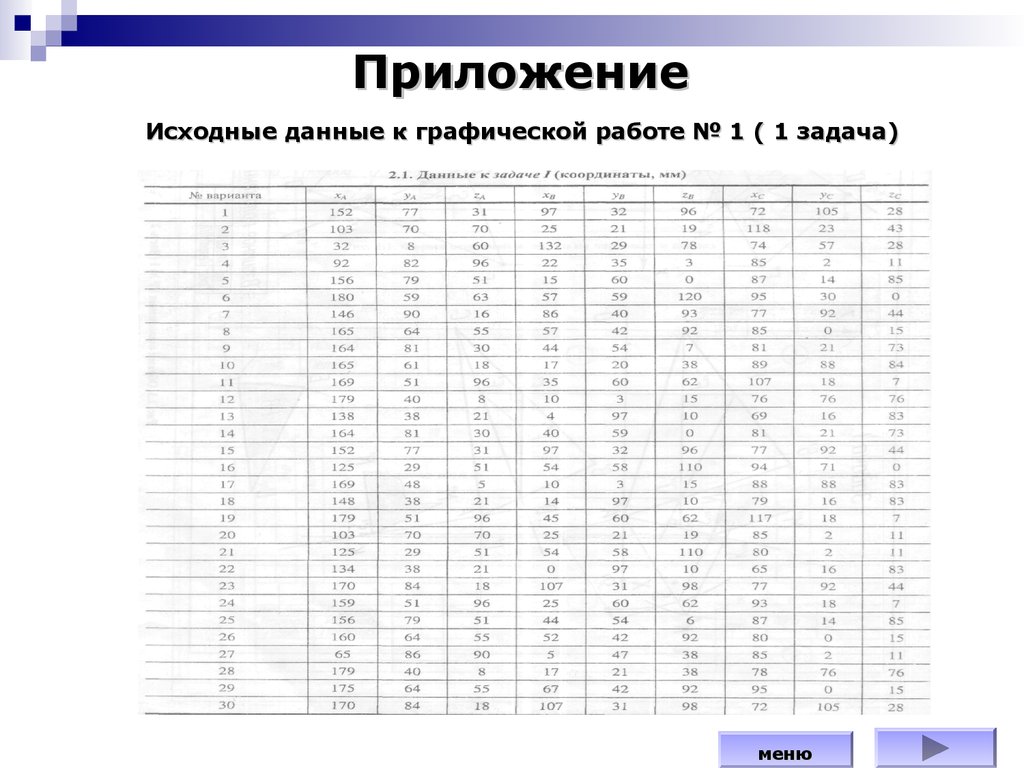
79.
ПриложениеИсходные данные к графической работе № 1 ( 1 задача)
меню
80.
Исходные данные к графической работе № 1 ( 2 задача)81.
Исходные данные к графической работе № 282.
Исходные данные к графической работе № 3 (лист №1)83.
Исходные данные к графической работе № 3 (лист №2)84.
Исходные данные к графической работе № 3 (лист №2)85.
Проверочный тестПравила
работы с тестом
Старт
Выход
в основное меню
86.
Тест № 1Тест № 2
Тест № 3
ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ.
СПОСОБЫ ПРЕОБРАЗОВАНИЯ
ЧЕРТЕЖА.
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ
ПОВЕРХНОСТЕЙ.
87.
ЗАПУСТИТЬТЕСТ №1
К МЕНЮ
88.
ЗАПУСТИТЬТЕСТ №2
К МЕНЮ
89.
ЗАПУСТИТЬТЕСТ №3
К МЕНЮ
90.
После запуска тестовой программы пользователюнеобходимо из предлагаемого перечня доступных
режимов, выбрать режим «ОБУЧЕНИЕ».
Вам предлагается ответить на 10 вопросов по 3
разделам учебного материала, на которые будут
даны варианты ответов. Подсчет баллов
осуществляется автоматически, после завершения
теста программа выдает результат по двухбалльной
системе «ЗАЧЕТ» «НЕ ЗАЧЕТ».














































 drafting
drafting








