Similar presentations:
Фигуры в пространстве. Движение в пространстве
1.
Теоретическая базаподготовлена 4 группой
Власкина Кристина, Жунусов Жанат, Иралин Рафаэль,
Михайлова Анна, Перебалин Захар, Старицына Алиса
2.
Понятие отображения пространства на себяПусть каждой точке X пространства поставлена в соответствие некоторая точка X1,
причем любая точка X1 пространства оказалась поставленной в соответствие какойто точке X. Тогда говорят, что задано отображение пространства на себя. При
данном отображении точка X переходит (отображается) в точку X1.
3.
Движение в пространствеДвижение в пространстве определяется так же, как и на плоскости.
Движением называется преобразование, при котором сохраняются расстояния
между точками.
Под движением пространства понимается отображение пространства на себя, при
котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что
|AB|=|A1B1|.
Иными словами, движение пространства — это отображение пространства на себя,
сохраняющее расстояния между точками. Так же, как и для движения на плоскости,
доказывается, что:
при движении в пространстве
- прямые переходят в прямые,
- полупрямые — в полупрямые,
- отрезки — в отрезки,
- сохраняются углы между прямыми.
4.
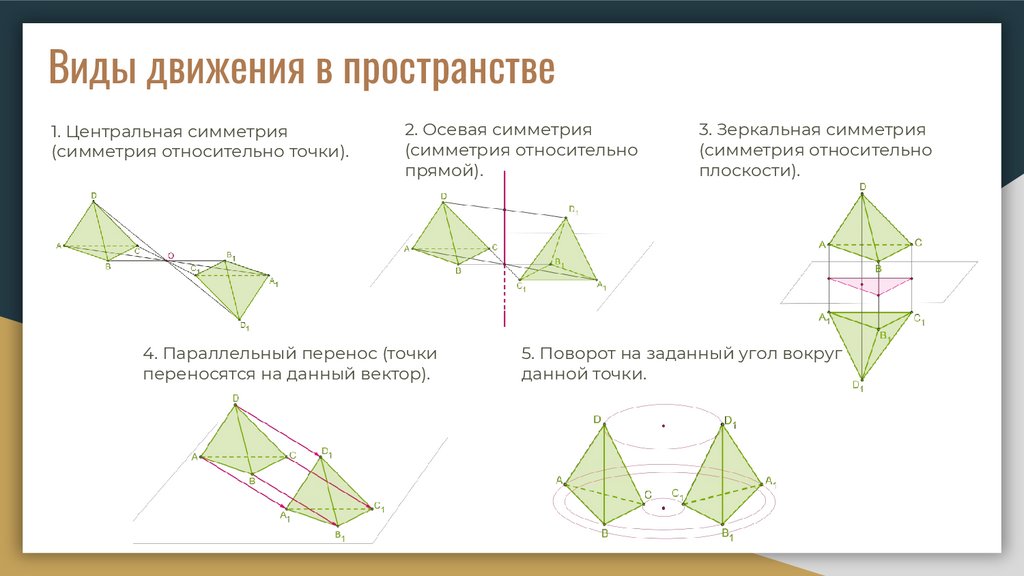
Виды движения в пространстве1. Центральная симметрия
(симметрия относительно точки).
2. Осевая симметрия
(симметрия относительно
прямой).
4. Параллельный перенос (точки
переносятся на данный вектор).
3. Зеркальная симметрия
(симметрия относительно
плоскости).
5. Поворот на заданный угол вокруг
данной точки.
5.
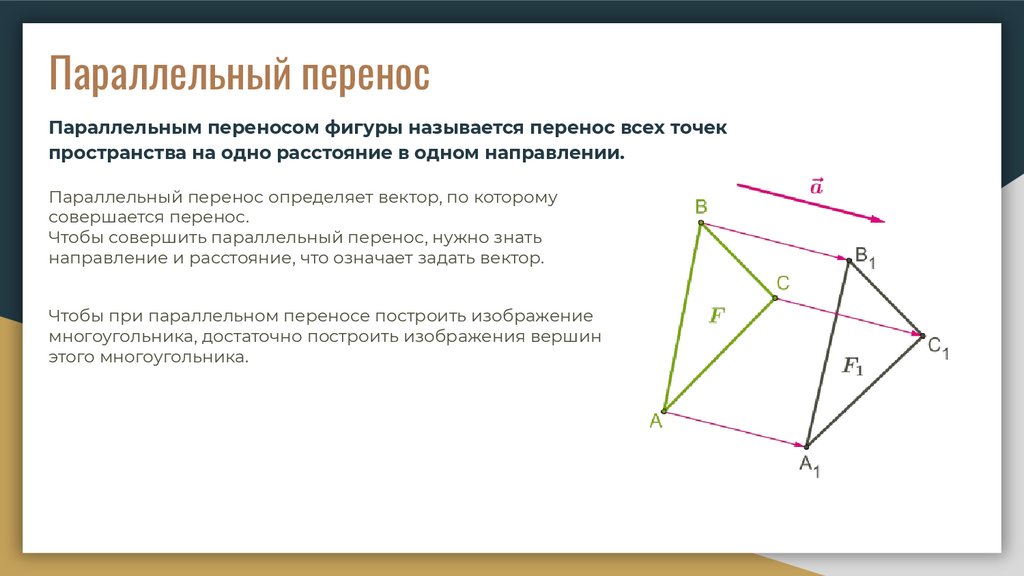
Параллельный переносПараллельным переносом фигуры называется перенос всех точек
пространства на одно расстояние в одном направлении.
Параллельный перенос определяет вектор, по которому
совершается перенос.
Чтобы совершить параллельный перенос, нужно знать
направление и расстояние, что означает задать вектор.
Чтобы при параллельном переносе построить изображение
многоугольника, достаточно построить изображения вершин
этого многоугольника.
6.
Параллельный переносПервоначальная фигура и фигура, полученная после параллельного переноса, равны.
Параллельный перенос используется для конструирования графиков функций.
На рисунке изображена парабола и два результата параллельного переноса.
Иногда параллельный перенос встречается в
необычных ситуациях.
7.
Изображение параллельного переноса впрямоугольной системе координат
Предположим, что система координат XOY перенесена параллельно себе так, что начало
координат сместилось в точку M(a;b). Найдем связь между координатами любой точки в старой и
новой системе координат. Возьмем произвольную точку N. В плоскости XOY она имеет
координаты N(x; y), в плоскости N(x’;y’) она имеет координаты X’O’Y’.
- преобразование координат при параллельном
переносе; выражение старых координат через
новые и новых через старые.
8.
Изображение параллельного переноса впрямоугольной системе координат. Пример
Рассмотрим уравнение:
Совершим параллельный перенос по
формулам
При этом начало координат перейдет в
точку O’(-1;-3). В новой системе координат
уравнение примет вид
В новой системе координат X’OY’
получено каноническое уравнение
гиперболы с параметрами a = 4, b = 2√2.
Построим старые и новые оси, а также
саму кривую.
9.
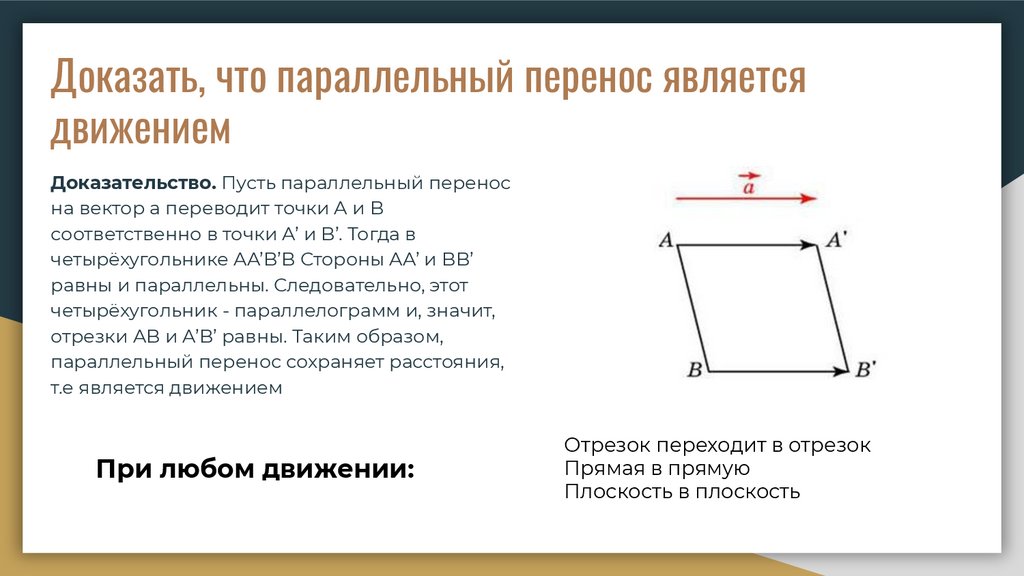
Доказать, что параллельный перенос являетсядвижением
Доказательство. Пусть параллельный перенос
на вектор a переводит точки A и B
соответственно в точки A’ и B’. Тогда в
четырёхугольнике AA’B’B Стороны AA’ и BB’
равны и параллельны. Следовательно, этот
четырёхугольник - параллелограмм и, значит,
отрезки AB и A’B’ равны. Таким образом,
параллельный перенос сохраняет расстояния,
т.е является движением
При любом движении:
Отрезок переходит в отрезок
Прямая в прямую
Плоскость в плоскость







 mathematics
mathematics








