Геометрические преобразование. Движение фигуры. Параллельный перенос

1.

Глава 5
Геометрические
преобразование
§ 17 Движение фигуры.
Параллельный перенос
- В этой главе вы узнаете, что такое
преобразование фигуры
- Познакомитесь с такими видами
преобразований: параллельный перенос,
центральная симметрия, осевая симметрия,
поворот, гомотетия, подобие
Автор: Филиппов Иван
Волобуева Вероника

2.

Пример 1
На этом рисунке каждой точке X
отрезка AB поставим в
соответствие точку X1 прямой а
так, чтобы точки O, X и X1 лежали
на одной прямой
- При этом, точка A будет
соответствовать точке A1, точке B –
точка B1.
КАК?
Мы указали правило, с помощью
которого каждой точке X отрезка AB
поставлена в соответствии
единственная точка X1 отрезка A1B1
! В этом случае говорят, что отрезок
A1B1 получен в результате
преобразования отрезка AB !
Если не учить геометрию, все кажется магией

3.

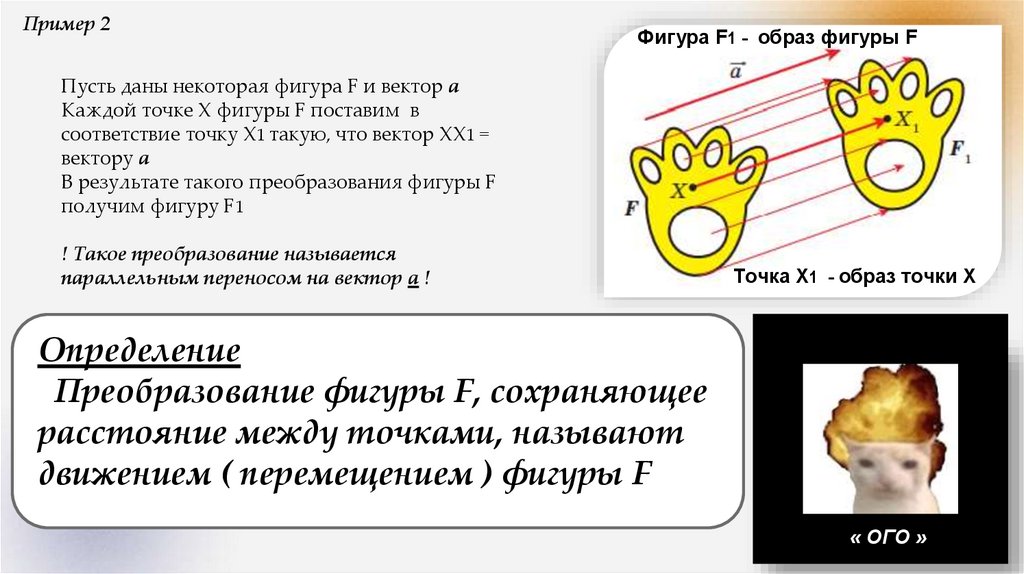
Пример 2
Фигура F1 - образ фигуры F
Пусть даны некоторая фигура F и вектор a
Каждой точке X фигуры F поставим в
соответствие точку X1 такую, что вектор XX1 =
вектору а
В результате такого преобразования фигуры F
получим фигуру F1
! Такое преобразование называется
параллельным переносом на вектор a !
Точка X1 - образ точки X
Определение
Преобразование фигуры F, сохраняющее
расстояние между точками, называют
движением ( перемещением ) фигуры F
« ОГО »

4.

Мы давно используем понятие « равенство фигур », хотя не давали строгого
определения
На то, что движение связано с равенством фигур, указывают следующие
свойства движения:
Если преобразование является движением, то:
- образом прямой является прямая
- образом отрезка является отрезок, равный данному
- образом угла является угол, равен данному
- образом треугольника является треугольник, равный данному
Определение
Две фигуры называют равными, если
существует движение, при котором одна
из данных фигур является образом другой
F = F1 – фигуры равны
« што? »

5.

Теорема гласит:
Параллельный перенос называется движением
Когда выучил теорему наизусть с первого раза:

6.

Рубрика докажи : теорема 17.1
Пусть A(x1; y1) и B(x2; y2) — произвольные точки фигуры F
Докажем, что AB = A1B
Если фигура F1 — образ
фигуры F при
параллельном переносе, то
F1 =F.

7.

Такое свойство применяется для тканей, обоев и
разнообразных принтов и т.д
Вапщета, не
только для
обоев и
принтов, но и
для проекции
изображений на
поверхность с
помощью
проектора

8.

ЗАДАЧИ

9.

10.

11.

Все!
Мы постарались сделать презентацию
информативной и прикольной
Старались как могли, Любовь Николаевна
:__)
Если что-то не поняли, самое
время задать вопросы!
Поможем разобраться
Если разобрались – молодцы!