Similar presentations:
Движение и подобие. Преобразования в пространстве
1. Движение и подобие.
Преобразования впространстве.
Движение и подобие.
2. Движение.
• Преобразование одной фигурыв другую называется
движением, если оно
• сохраняет расстояние между
точками.
• Другими словами, если точки Х
и Y фигуры F перешли в точки
X1 и Y1 фигуры F1, то XY=X1Y1.
3. Свойства движения:
• При движении в пространстве:• Прямые переходят в прямые.
• Полупрямые – в полупрямые.
• Отрезки - в отрезки.
• Сохраняются углы между
полупрямыми.
Новое свойство:
• Движение переводит плоскость в
плоскость.
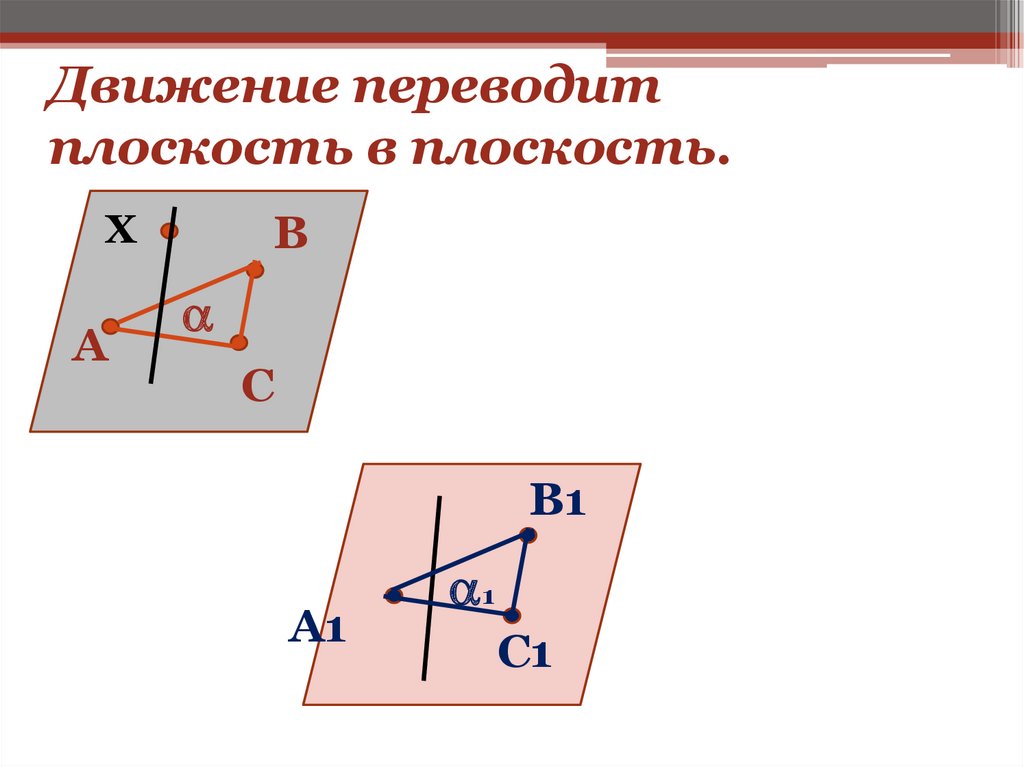
4. Движение переводит плоскость в плоскость.
ХА
В
С
В1
А1
1
С1
5. Виды движений:
•Симметрии (центральная,осевая, зеркальная)
•Параллельный перенос
•Поворот
6. «Симметрия… есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». Герман
Вейль.О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
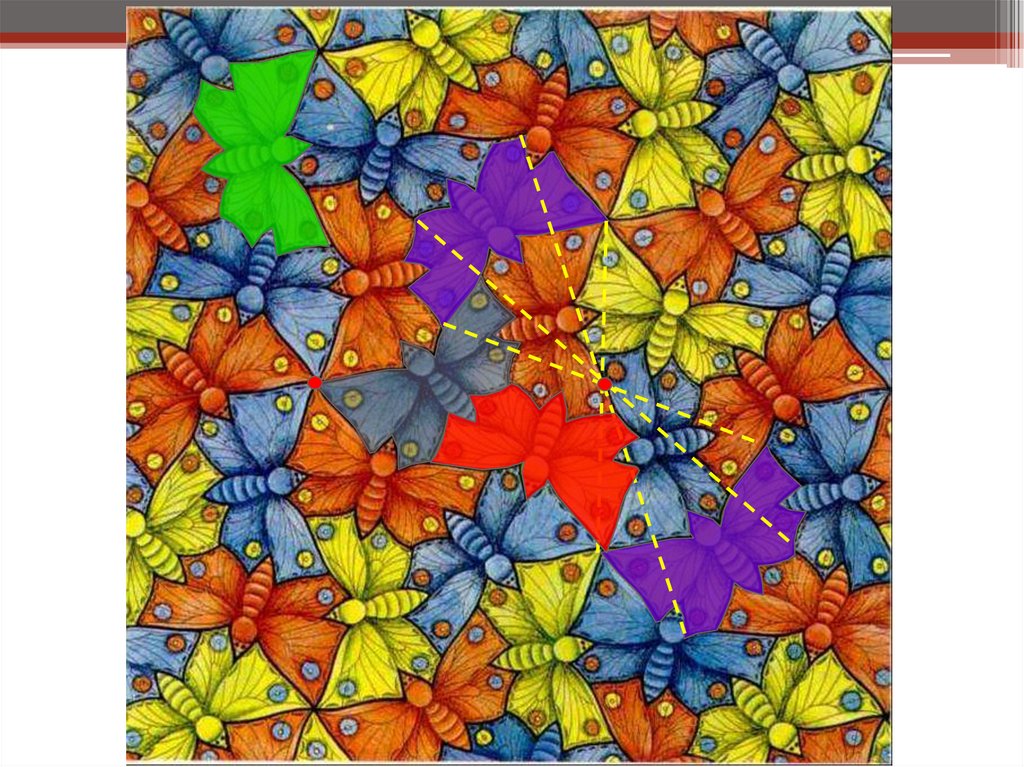
7. Орнаменты
• Много причудливыхмозаик – орнаментов
создала фантазия
знаменитого
голландского художника
Мариуса Эшера (18981972 гг).
• Основой его орнаментов
являются изображения
птиц, животных, людей,
растений.
8.
9. Преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1 фигуры F1,называется
1.симметриейотносительно
точки
(центральной
симметрией),
если
10. Симметрия относительно точки А: преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1
фигуры F1,симметричную Х относительно точки А:
Х
Х1
если Асередина
отрезка ХХ1
11. В какую фигуру отображается при центральной симметрии прямая, не проходящая через центр?
проходящая через центр?• Прямая
Х1
переходит в
О
У
Х
У1
12. В какую фигуру отображается при центральной симметрии плоскость, не проходящая через центр?
проходящая через центр?• плоскость
Х1
переходит в
О
У
Х
У1
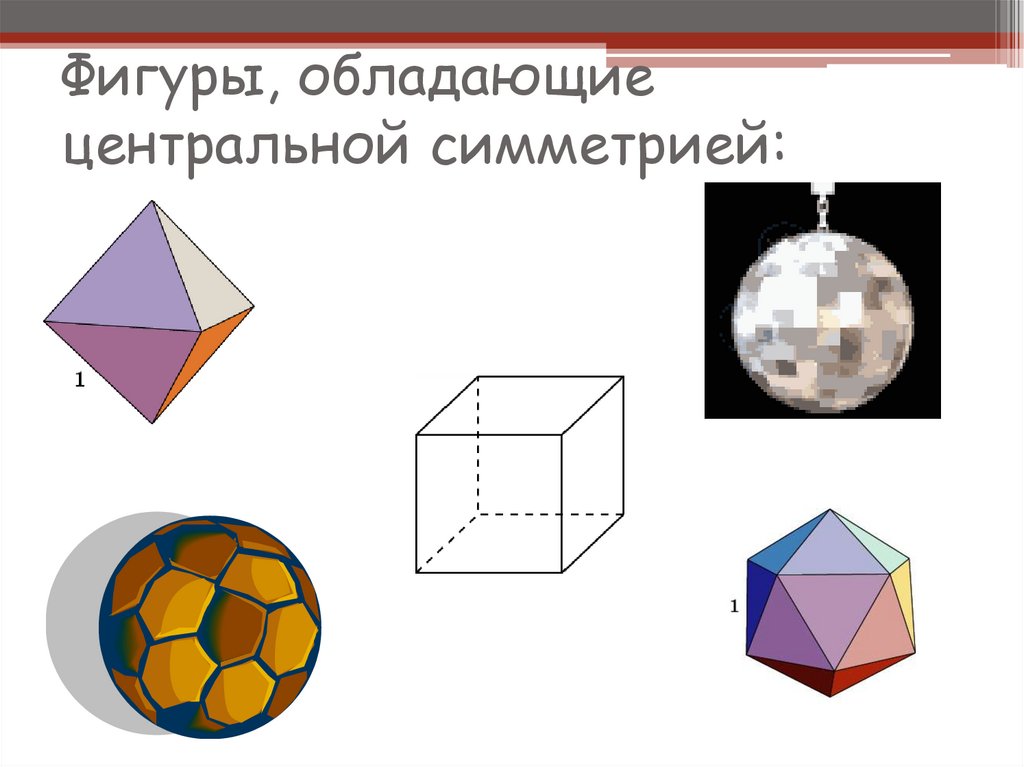
13. Фигуры, обладающие центральной симметрией:
14. Кристаллы
15. Центральная симметрия в природе:
16. Центральная симметрия в природе:
17. Преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1 фигуры F1,называется
2.симметриейотносительно
прямой (осевой
симметрией),
если
18. Симметрия относительно прямой а: преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1
фигуры F1,симметричную Х относительно прямой а
Х1
а
Х
прямая а
перпендикулярна
отрезку ХХ1 и
делит его
пополам.
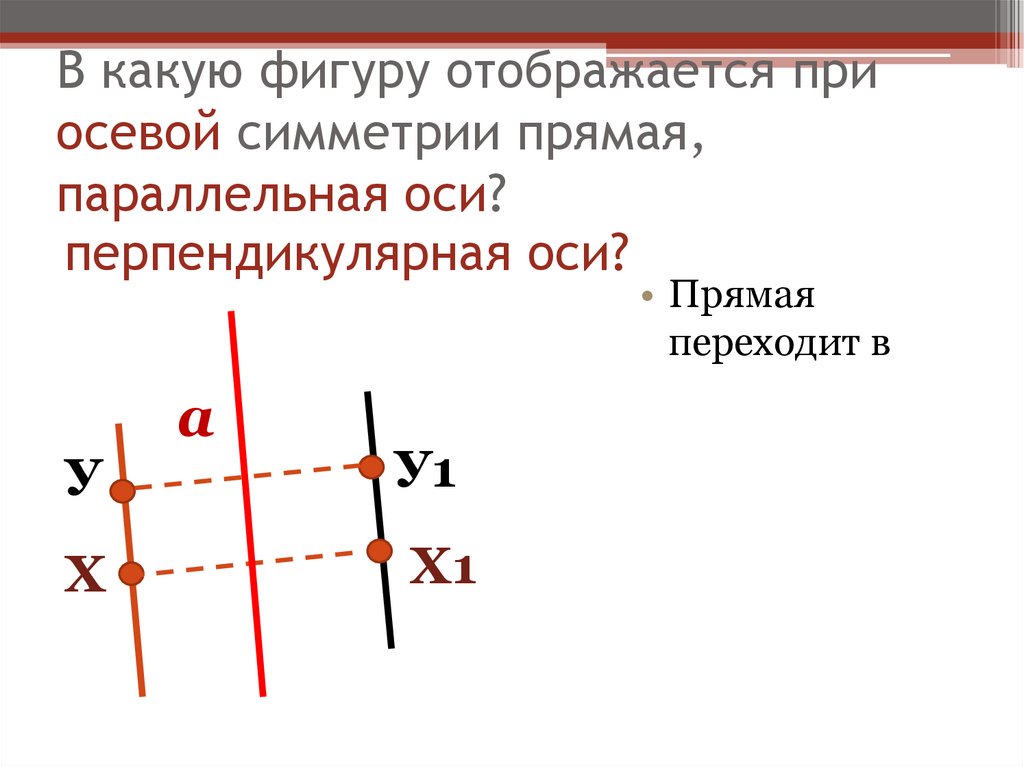
19. В какую фигуру отображается при осевой симметрии прямая, параллельная оси?
перпендикулярная оси?• Прямая
переходит в
У
Х
а
У1
Х1
20. Симметрия в искусстве
• Прекрасные симметриидемонстрируют
произведения искусства:
архитектуры, живописи,
скульптуры и т.д.
• Элементы симметрии
можно увидеть в общих
планах зданий,
архитектуры фасадов, в
оформлении внутренних
помещений, колоннах,
потолках и т.д.
21. Искусство
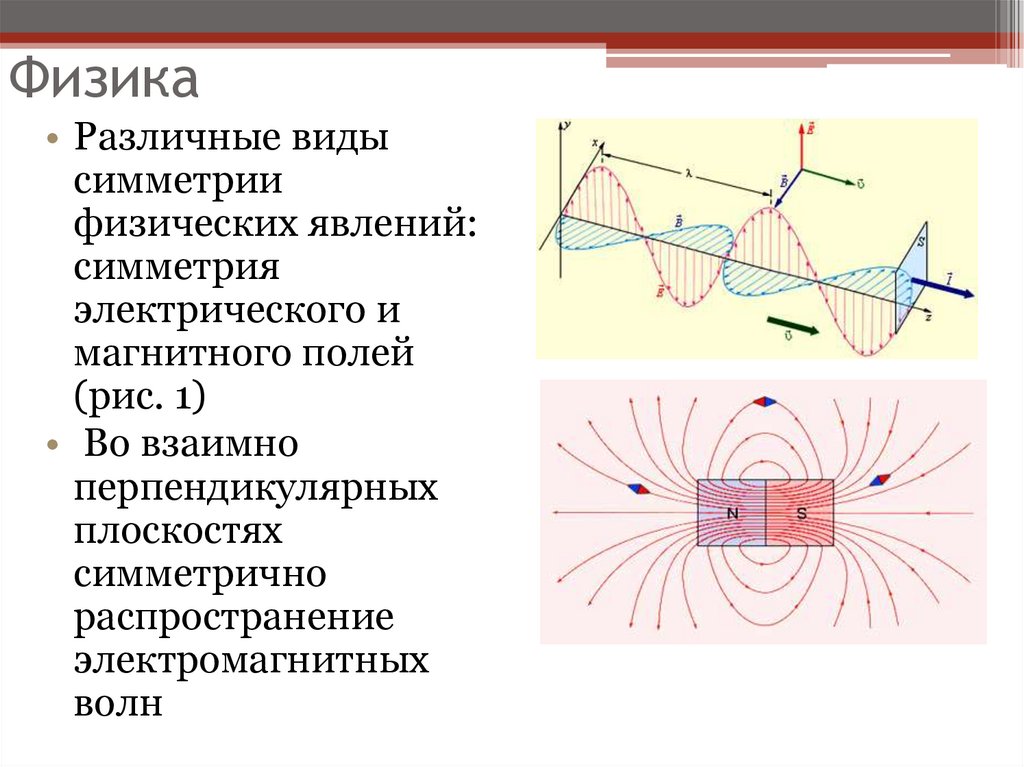
22. Физика
• Различные видысимметрии
физических явлений:
симметрия
электрического и
магнитного полей
(рис. 1)
• Во взаимно
перпендикулярных
плоскостях
симметрично
распространение
электромагнитных
волн
23. Преобразования в пространстве.
Зеркальная симметрия.Преобразования
в
пространстве.
24. Преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1 фигуры F1,называется
3.симметриейотносительно
плоскости
(зеркальной
симметрией),
если
25. Симметрия относительно плоскости : преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку
Симметрия относительно плоскости :преобразование фигуры F в фигуру F1,
при котором каждая точка Х фигуры F
переходит в точку Х1 фигуры F1,
симметричную Х относительно плоскости
Х1
О Х
плоскость
перпендикулярна
отрезку ХХ1 и
делит его
пополам.
26.
• Предметы могут иметь одну, две, три и т.д.плоскостей симметрии. Например, прямая
пирамида, основанием которой является
равнобедренный треугольник, симметрична
относительно одной плоскости. Призма с таким
же основанием имеет две плоскости симметрии. У
правильной шестиугольной призмы их семь.
27.
Прекрасныеобразы
симметрии
демонстрируют
произведения
искусства:
архитектуры…
28.
29.
30. …скульптуры.
31.
32. Архитектура
• Издавна человек использовалсимметрию в архитектуре. Особенно
блистательно использовали симметрию
в архитектурных сооружениях древние
зодчие. Причем древнегреческие
архитекторы были убеждены, что в своих
произведениях они руководствуются
законами, которые управляют природой.
Выбирая симметричные формы,
художник тем самым выражал свое
понимание природной гармонии как
устойчивости и равновесия.
33. Зеркальная симметрия в жизни
С этим видомсимметрии мы
сталкиваемся
чаще всего,
например, когда
смотрим в
зеркало.
34.
Следует отметить, что двесимметричные фигуры
или две симметричные
части одной фигуры при
всем их сходстве, равенстве
объемов и площадей
поверхностей, в общем
случае, неравны, т.е. их
нельзя совместить друг с
другом. Это разные
фигуры, их нельзя
заменить друг другом,
например, правая
перчатка, ботинок и т.д. не
годятся для левой руки,
ноги.
35.
36. Параллельный перенос
37.
Параллельный перенос38.
39.
40. Преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1 фигуры F1,называется
4.параллельным
переносом,
если
41. Параллельный перенос : преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1 фигуры F1,
Хесли Х(х;у;z) Х1,
Х1(х+а;у+b;z+c),
где числа а; b и c
одни и те же для
Х1
всех точек.
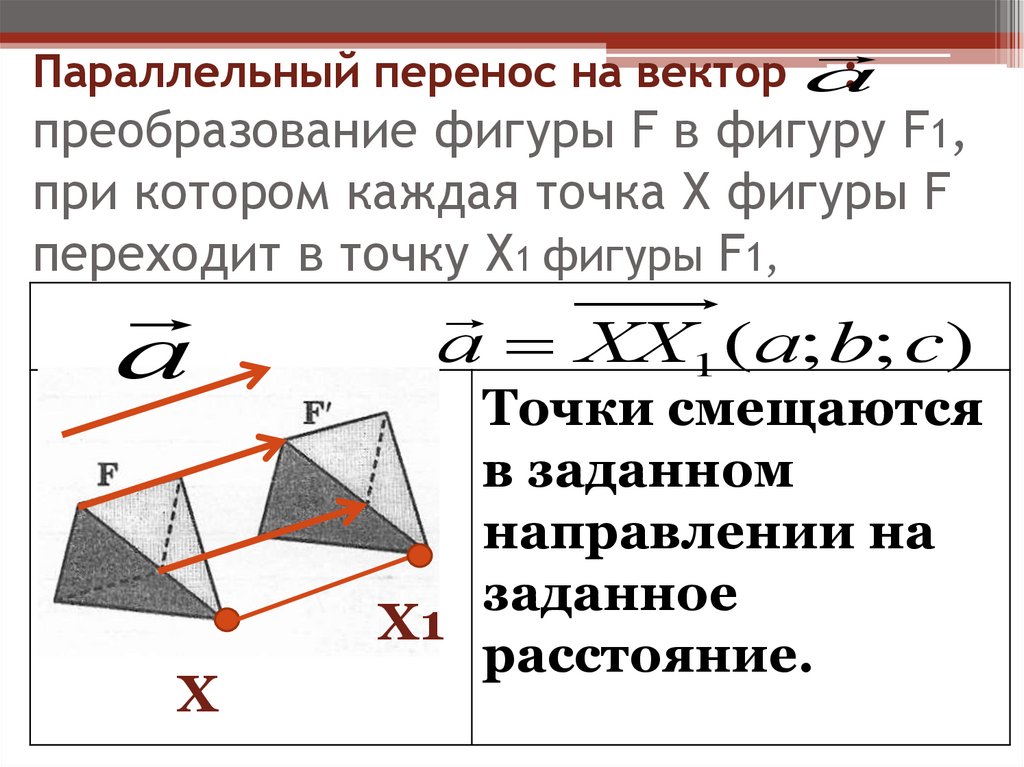
42. Параллельный перенос на вектор : преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1
Параллельный перенос на вектор а:
преобразование фигуры F в фигуру F1,
при котором каждая точка Х фигуры F
переходит в точку Х1 фигуры F1,
а
Х
а ХХ1 (а; b; c)
Точки смещаются
в заданном
направлении на
заданное
Х1
расстояние.
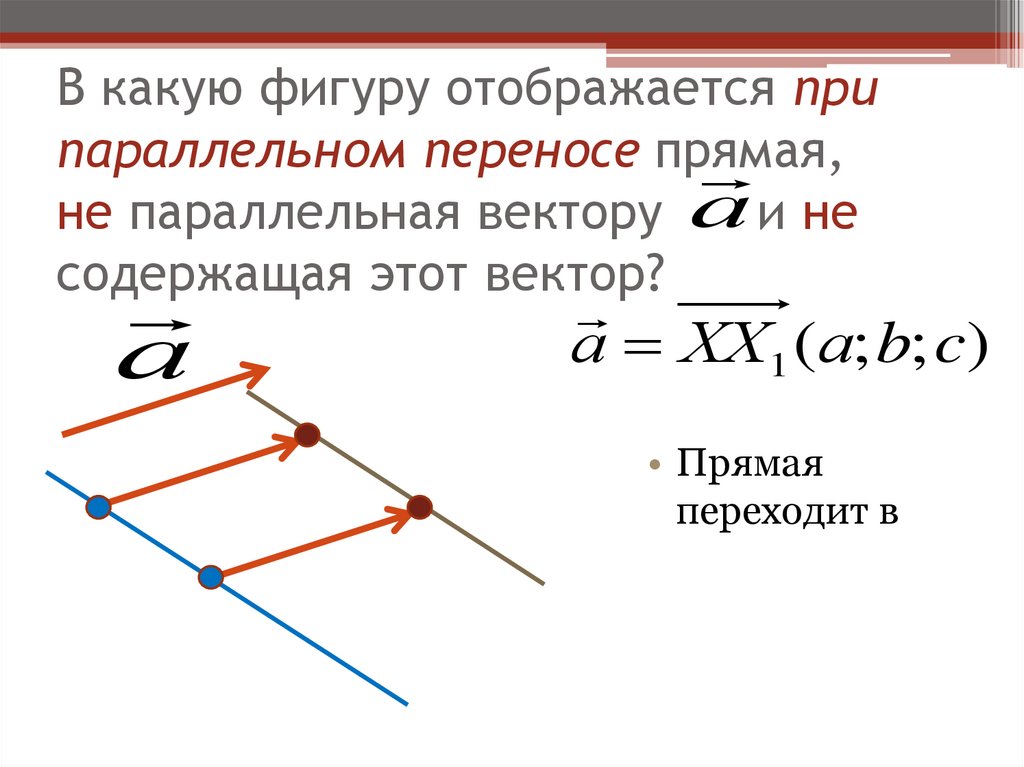
43. В какую фигуру отображается при параллельном переносе прямая, не параллельная вектору и не содержащая этот вектор?
В какую фигуру отображается припараллельном переносе прямая,
не параллельная вектору а и не
содержащая этот вектор?
а
а ХХ1 (а; b; c)
• Прямая
переходит в
44. В какую фигуру отображается при параллельном переносе прямая, параллельная вектору или содержащая этот вектор?
В какую фигуру отображается припараллельном переносе прямая,
параллельная вектору а или
содержащая этот вектор?
а
а ХХ1 (а; b; c)
• Прямая
переходит в
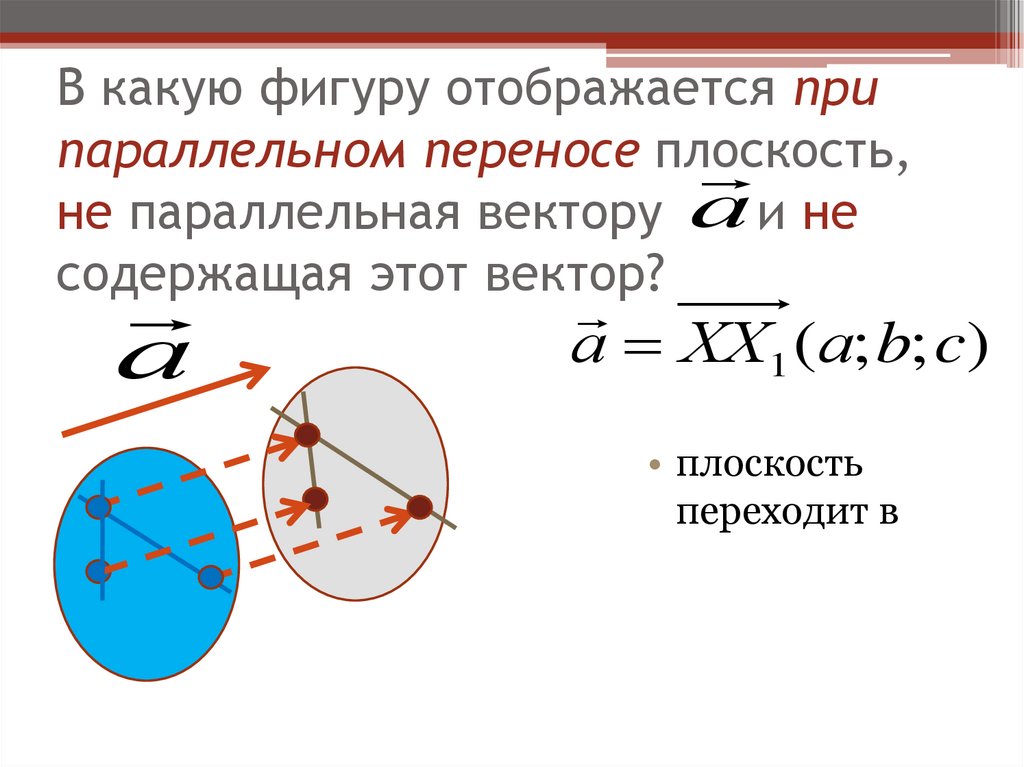
45. В какую фигуру отображается при параллельном переносе плоскость, не параллельная вектору и не содержащая этот вектор?
В какую фигуру отображается припараллельном переносе плоскость,
не параллельная вектору а и не
содержащая этот вектор?
а
а ХХ1 (а; b; c)
• плоскость
переходит в
46. В какую фигуру отображается при параллельном переносе плоскость, параллельная вектору или содержащая этот вектор?
В какую фигуру отображается припараллельном переносе плоскость,
параллельная вектору а или
содержащая этот вектор?
а
а ХХ1 (а; b; c)
• плоскость
переходит в
47. Особые свойства параллельного переноса :
• При параллельном переносе:• точки смещаются по параллельным (или
совпадающим) прямым на одно и то же
расстояние.
• прямая переходит в параллельную
прямую (или в себя).
• плоскость переходит в параллельную ей
плоскость (либо в себя).
• Каковы бы ни были две точки A и A1,
существует один и только один
параллельный перенос, при котором
точка A переходит в точку A1.
48. Параллельный перенос.
• Если движение не оставляет ни однойнеподвижной точки, то это движение и
есть параллельный перенос. Таким
образом, при параллельном переносе нет
неподвижных точек.
49.
Реальным примеромфигур,
полученных друг из друга
параллельным переносом,
являются одинаковые окна
на фасаде дома. Начертив
на плане одно из окон,
можно затем получить
любое другое окно,
сместив все точки первого
в одном и том же
направлении
на одно и то же
расстояние.
Это свойство и определяет
параллельный перенос.
50.
51. Преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F переходит в точку Х1 фигуры F1,называется
5. гомотетией,если
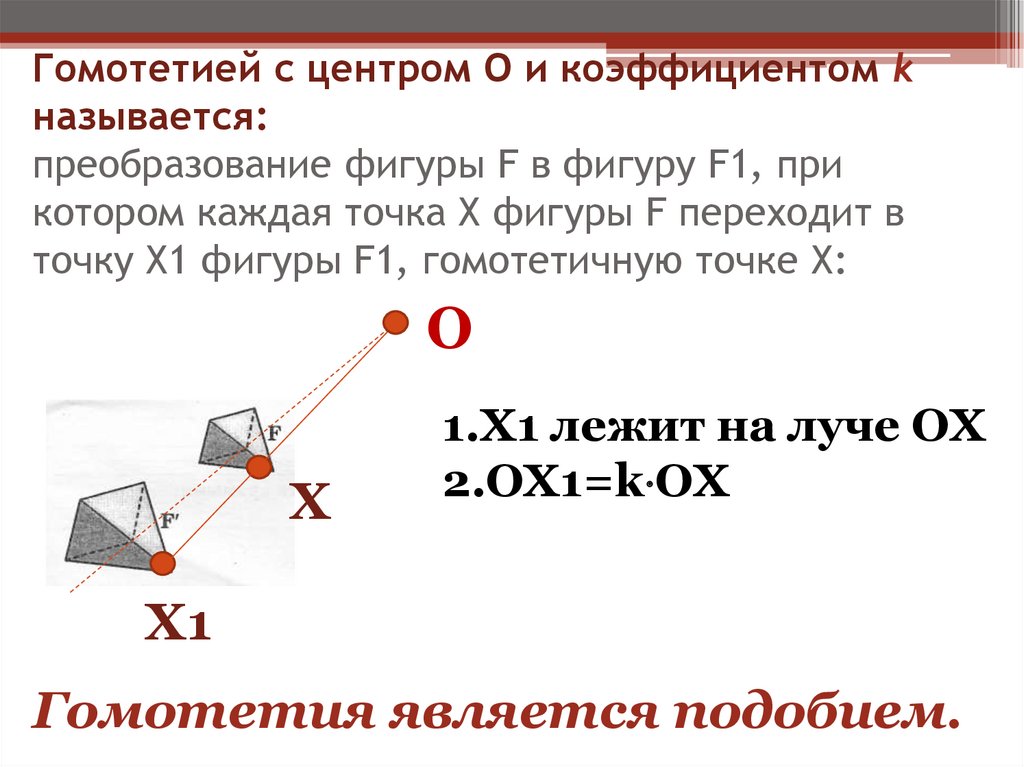
52. Гомотетией с центром О и коэффициентом k называется: преобразование фигуры F в фигуру F1, при котором каждая точка Х фигуры F
переходит вточку Х1 фигуры F1, гомотетичную точке Х:
O
Х
1.Х1 лежит на луче ОХ
2.ОХ1=k OX
Х1
Гомотетия является подобием.
53. Преобразование подобия с коэффициентом k
• Преобразование одной фигуры вдругую называется преобразованием
подобия с коэффициентом k, если оно
изменяет расстояние между точками в
k раз. Другими словами, если точки Х и
Y фигуры F перешли в точки X1 и Y1
фигуры F1, то XY= k X1Y1
54. Две фигуры называются подобными, если они переводятся одна в другую
• с помощью преобразования подобия.55. Как можно задать преобразование пространства?
указатьПри центральной
симметрии
При осевой
симметрии
При зеркальной
симметрии
При параллельном
переносе
При гомотетии
56. Какие точки при преобразовании остаются неподвижными, т.е. совпадают со своим образом?
При центральнойсимметрии
При осевой
симметрии
При зеркальной
симметрии
При параллельном
переносе
При гомотетии
57. Преобразования симметрии в координатах :
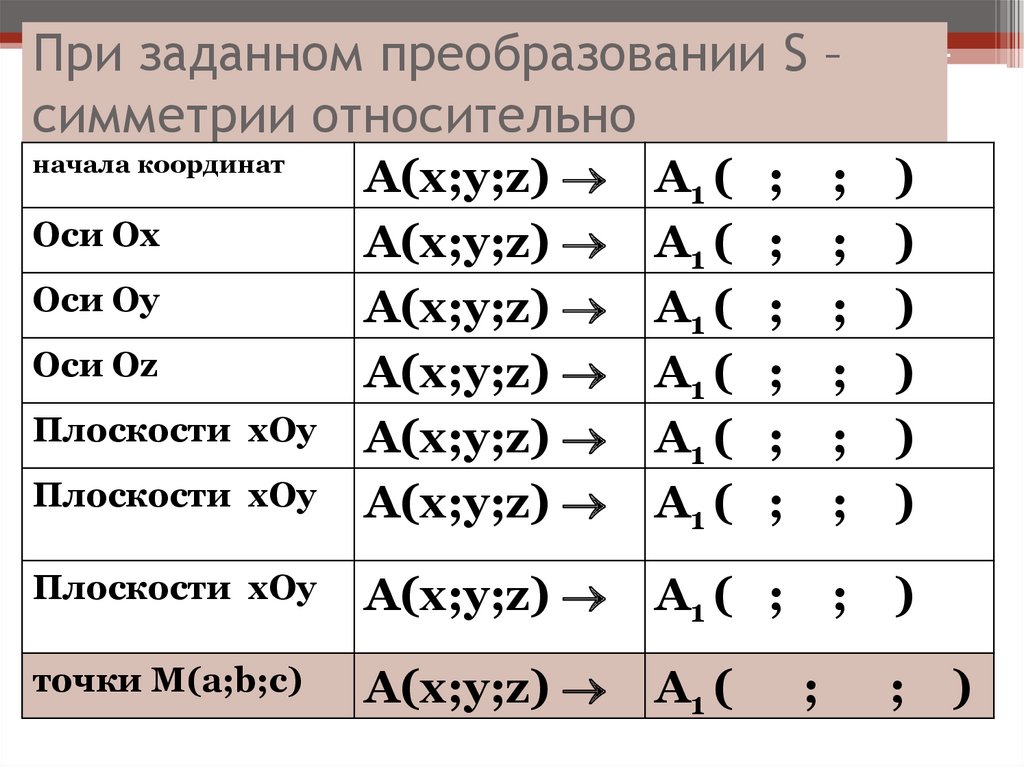
58. При заданном преобразовании S – симметрии относительно
Плоскости хОуА(x;y;z)
А(x;y;z)
А(x;y;z)
А(x;y;z)
А(x;y;z)
А(x;y;z)
A1 (
A1 (
A1 (
A1 (
A1 (
A1 (
;
;
;
;
;
;
;
;
;
;
;
;
)
)
)
)
)
)
Плоскости хОу
А(x;y;z)
A1 ( ;
;
)
точки М(a;b;c)
А(x;y;z)
A1 (
начала координат
Оси Ох
Оси Оу
Оси Оz
Плоскости хОу
;
;
)
59. Симметрия относительно начала координат: А(х;у;z)
Симметрия относительно началакоординат: А(х;у;z)
z
B(2;-1;2)
О
1
K
3
N
х
C(-2;1,5;1,5)
М
2
А(х;у;z)
у
60. Симметрия относительно осей координат: А(х;у;z)
Симметрия относительно осейкоординат: А(х;у;z)
z
B(2;-1;2)
О
1
K
3
N
х
C(-2;1,5;1,5)
М
у
2
А(х;у;z) А1( ; ; )
А(х;у;z) А1( ; ; )
А(х;у;z) А1( ; ; )
61. Симметрия относительно координатных плоскостей:
zB(2;-1;2)
О
1
K
3
N
х
C(-2;1,5;1,5)
М
у
2
А(х;у;z) А1( ; ; )
А(х;у;z) А1( ; ; )
А(х;у;z) А1( ; ; )
62. При заданном преобразовании S – симметрии относительно
Плоскости хОzА(x;y;z)
А(x;y;z)
А(x;y;z)
А(x;y;z)
А(x;y;z)
А(x;y;z)
A1 (-x;-y;-z)
A1 (x; -y; -z)
A1 (-x;y; -z)
A1 (-x; -y;z)
A1 (x;y; -z)
A1 (x; -y;z)
Плоскости yОz
А(x;y;z)
A1 (-x;y;z)
точки М(a;b;c)
А(x;y;z)
A1 (
начала координат
Оси Ох
Оси Оу
Оси Оz
Плоскости хОу
;
;
)





















































 mathematics
mathematics








