Similar presentations:
Движения
1. Движения
учитель математикиСидоренко Н.А.
МБОУ»Школа №70
г.Казань
2. Преобразование одной фигуры в другую называется движением, в том случае, если оно сохраняет расстояние между точками.
Преобразование одной фигуры в другуюназывается д в и ж е н и е м , в том случае, если
оно сохраняет расстояние между точками.
A
A1
B
B1
AB = A1B1
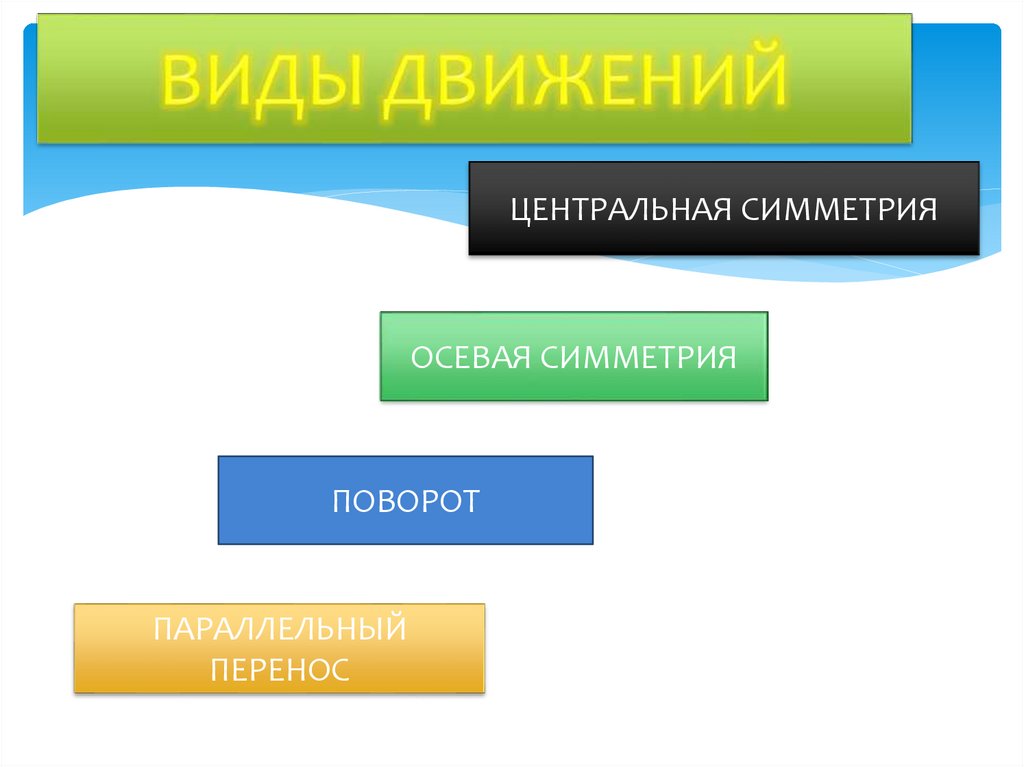
3. ВИДЫ ДВИЖЕНИЙ
ЦЕНТРАЛЬНАЯ СИММЕТРИЯОСЕВАЯ СИММЕТРИЯ
ПОВОРОТ
ПАРАЛЛЕЛЬНЫЙ
ПЕРЕНОС
4. СВОЙСТВА ДВИЖЕНИЯ
1)При движениипрямые переходят в
прямые, полупрямые –
в полупрямые,
отрезки – в отрезки.
2) Точки, лежащие на
одной прямой,
переходят в точки,
лежащие на другой
прямой, и порядок их
5. Движение плоскости – это отображение плоскости на себя, сохраняющее расстояние. Наложение- это отображение плоскости на себя.
Два движения, выполненные последовательно,снова дают движение.
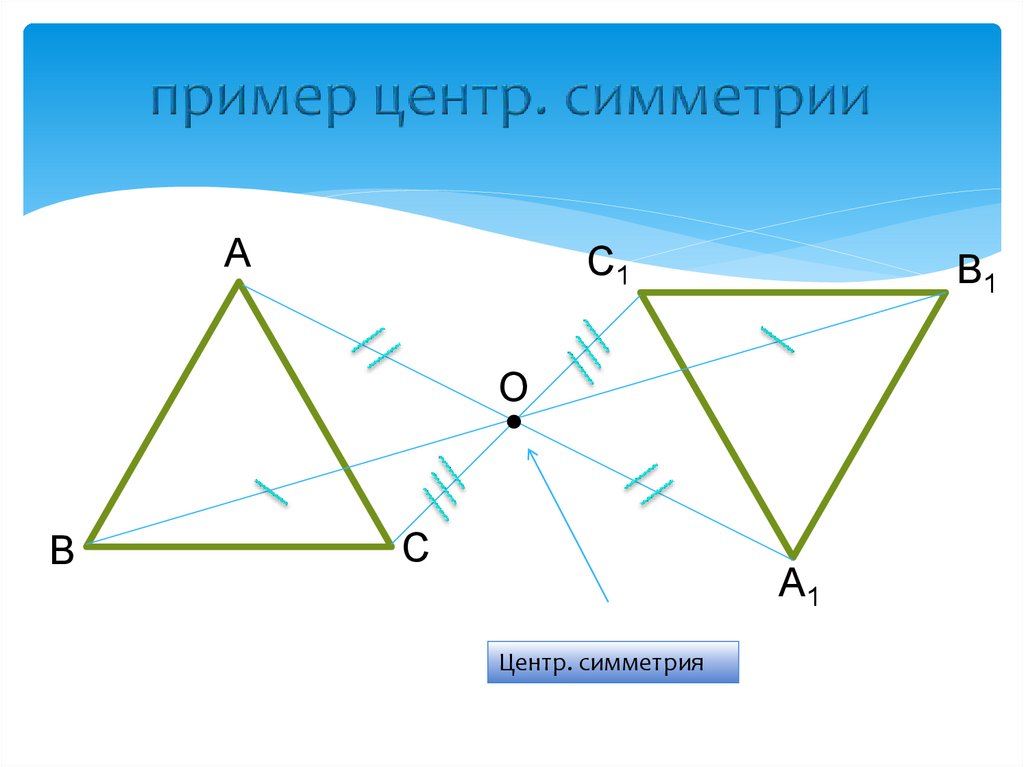
6. пример центр. симметрии
АС1
В1
О
В
С
А1
Центр. симметрия
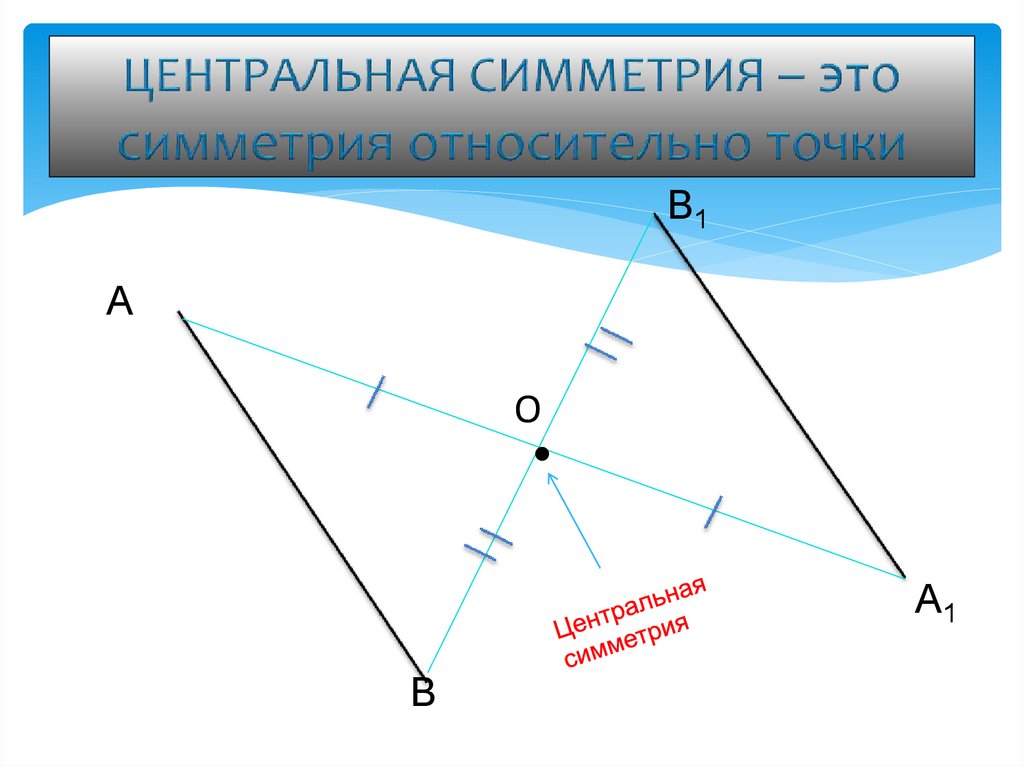
7. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – это симметрия относительно точки
В1А
О
А1
В
8. Свойства центральной симметрии.
Центральная симметрия на плоскости, как иповорот, сохраняет ориентацию.
Центральную симметрию в трёхмерном
пространстве называют также сферической
симметрией.
центральная симметрия является движением,
которое изменяет направления векторов на
противоположное.
Характерные свойства переноса и центральной
симметрии позволяют легко установить, каким
движением является любая композиция переносов
и центральных симметрий.(изометрии).
Центральной симметрией с центром О называется
такое преобразование фигуры, которое каждой ее
точке А сопоставляет точку А1, симметричную ей
относительно точки O.
9. В итоге: Чтобы построить фигуру, симметричную данной относительно точки О, нужно: 1)) каждую точку фигуры соединить с точкой О
2)продолжить полученный отрезок равным ему3)отметить на конце этого отрезка образ исходной
точки, затем соединить полученные образы.
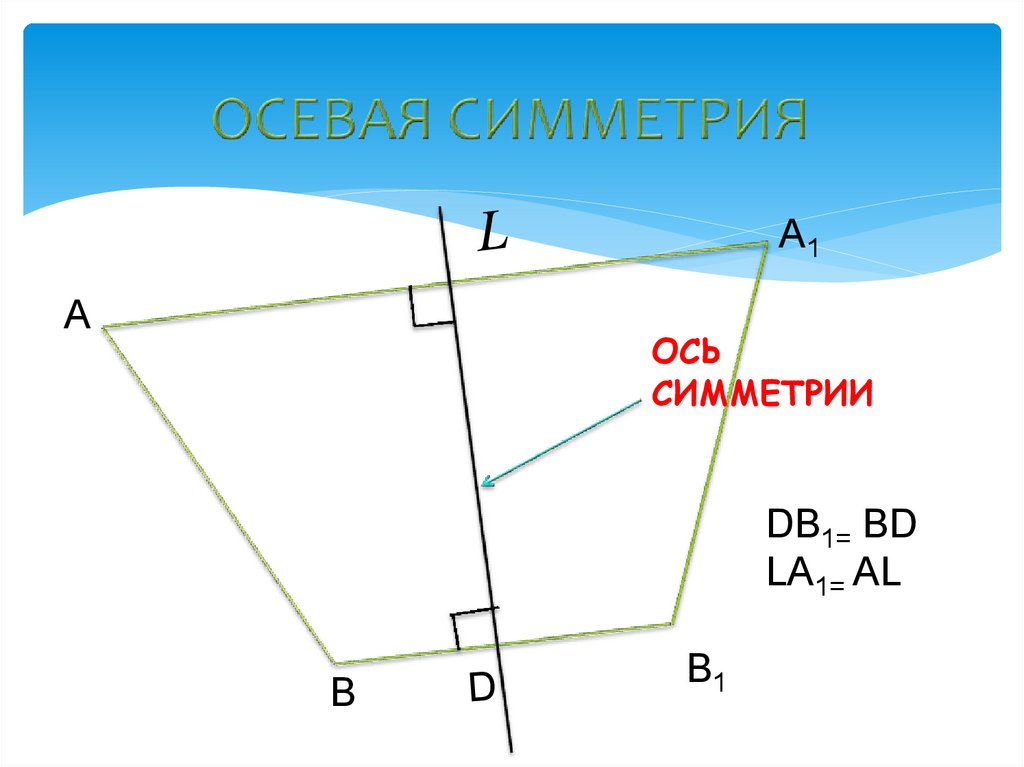
10. ОСЕВАЯ СИММЕТРИЯ
А1А
ОСЬ
СИММЕТРИИ
DB1= BD
LА1= AL
В
B1
11. Свойства осевой симметрии.
Осевая симметрия пространства есть движение, а значит, обладает всемисвойствами движений: переводит прямую в прямую, отрезок ---в отрезок,
луч ---в луч, плоскость ---в плоскость.
Кроме того, это преобразование пространства, совпадающее со своим
обратным: композиция двух симметрий относительно одной и той же
прямой есть тождественное преобразование.
При симметрии относительно прямой все точки этой прямой, и только они,
остаются на месте (неподвижные точки преобразования) . Прямые и
плоскости, перпендикулярные оси симметрии, переходят в себя.
Осевая симметрия есть поворот относительно оси симметрии на
определенный угол .
12. При осевой симметрии: --- неподвижной является каждая точка оси симметрии и других неподвижных точек не существует; ---
неподвижной прямой является ось симметрии (на ней индуцируетсятождественное преобразование) и любая прямая, пересекающая ось
симметрии и ей перпендикулярная (на каждой из этих прямых индуцируется
центральная симметрия относительно точки ее пересечения с осью
симметрии) ;
--- неподвижной является любая плоскость, перпендикулярная оси (в каждой
такой плоскости индуцируется центральная симметрия относительно точки ее
пересечения с осью симметрии) ;
При осевой симметрии:
13. Осевая симметрия- симметрия относительно прямой. чтобы построить фигуру, симметричную данной относительно прямой LD, нужно: 1)
из каждой точки фигуры провести перпендикуляр кпрямой LD.
2) продолжить полученный отрезок равным ему,
3) отметить на конце этого отрезка образ исходной
точки, затем соединить полученные образы.
FINISH
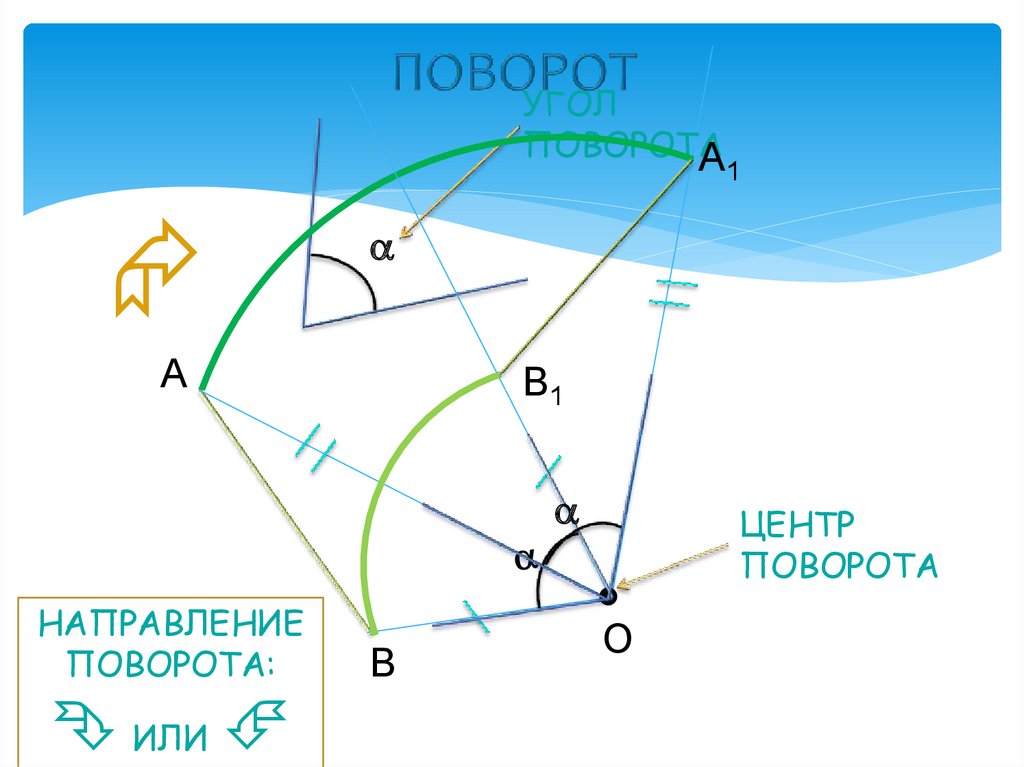
14. ПОВОРОТ
УГОЛПОВОРОТА
А
1
А
В1
НАПРАВЛЕНИЕ
ПОВОРОТА:
ИЛИ
В
ЦЕНТР
ПОВОРОТА
О
15. ПОВОРОТ - движение, при котором по крайней мере одна точка плоскости (пространства) остаётся неподвижной.
Чтобы получить отображение фигуры при повороте околоданной точки, нужно:
1) каждую точку фигуры повернуть на один и тот же угол в
одном и том же направлении (по часовой стрелке или
против часовой стрелки)
2) P.s. при движении угол переходит в равный ему угол.
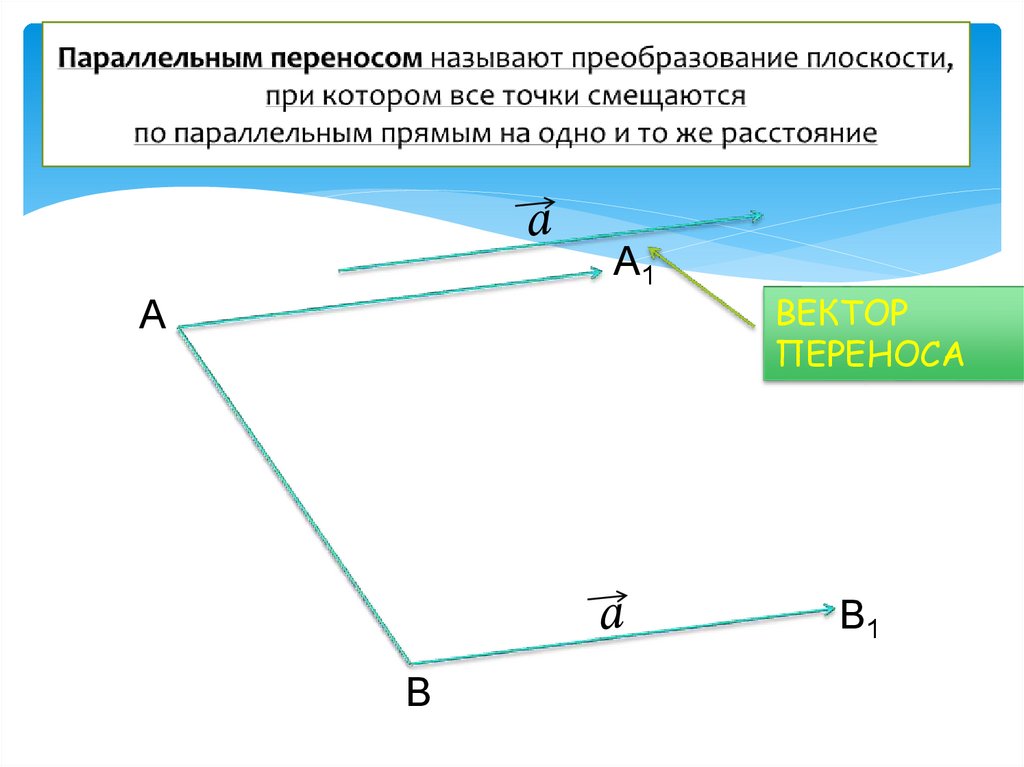
16. Параллельным переносом называют преобразование плоскости, при котором все точки смещаются по параллельным прямым на одно и то
А1А
ВЕКТОР
ПЕРЕНОСА
В1
В
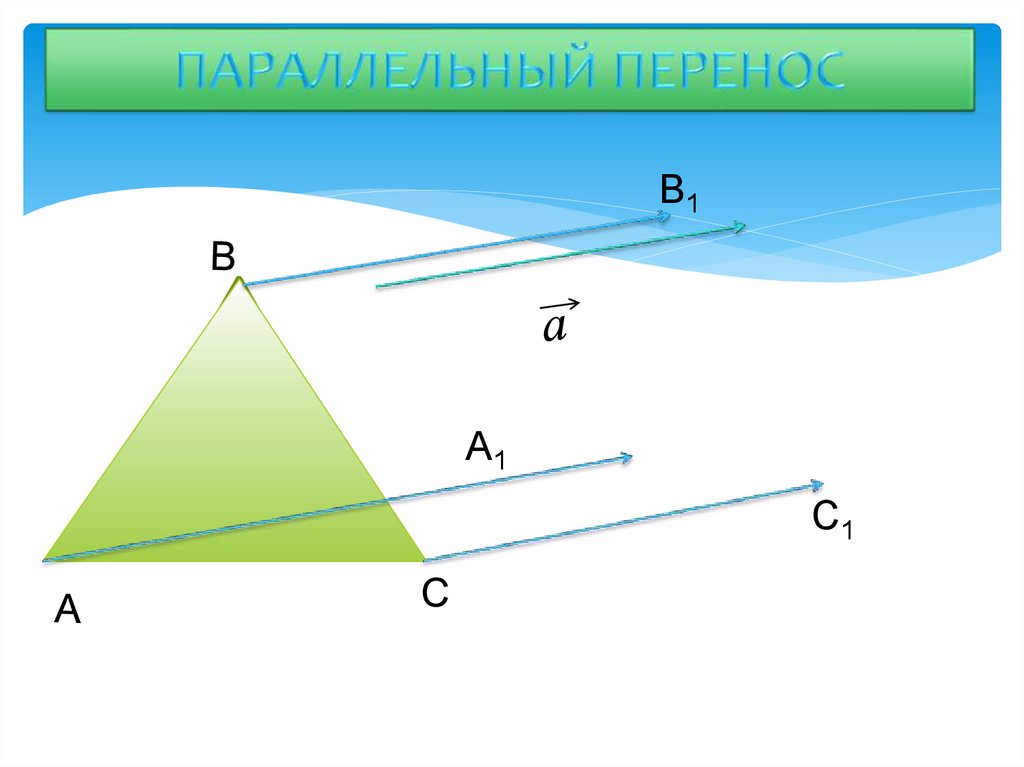
17. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
В1А1
С1
18. Свойства параллельного переноса.
У параллельного переноса нет неподвижных точек.Параллельным переносом на некоторый заданный
вектор называется такое отображение плоскости на саму
себя, при котором каждая точка А плоскости переходит в
такую точку А1 той же плоскости, чтобы АА1= а
Значит, расстояние между векторами и точками равно.
Таким образом, параллельный перенос сохраняет расстояние
между точками и поэтому представляет собой движение.
Параллельный перенос перемещает каждую точку фигуры или
пространства на одно и то же расстояние в одном и том же направлении.
При параллельном переносе прямая переходит либо в себя, либо в
параллельную ей прямую.
Параллельный перенос задается парой соответствующих точек, т.е.
каковы бы ни были точки, существует единственный параллельный
перенос, при котором точка переходит в точку.
19. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Сделаем вывод:
Чтобы отобразить фигуру с помощьюпараллельного переноса, нужно:
1) каждую точку фигуры переместить на заданный
вектор
2) соединить полученные образы
20.
Внимание!Любая фигура переходит
в равную ей фигуру
Фигуры называются равными,
если существует движение ,
отображающее одну из них на другую.
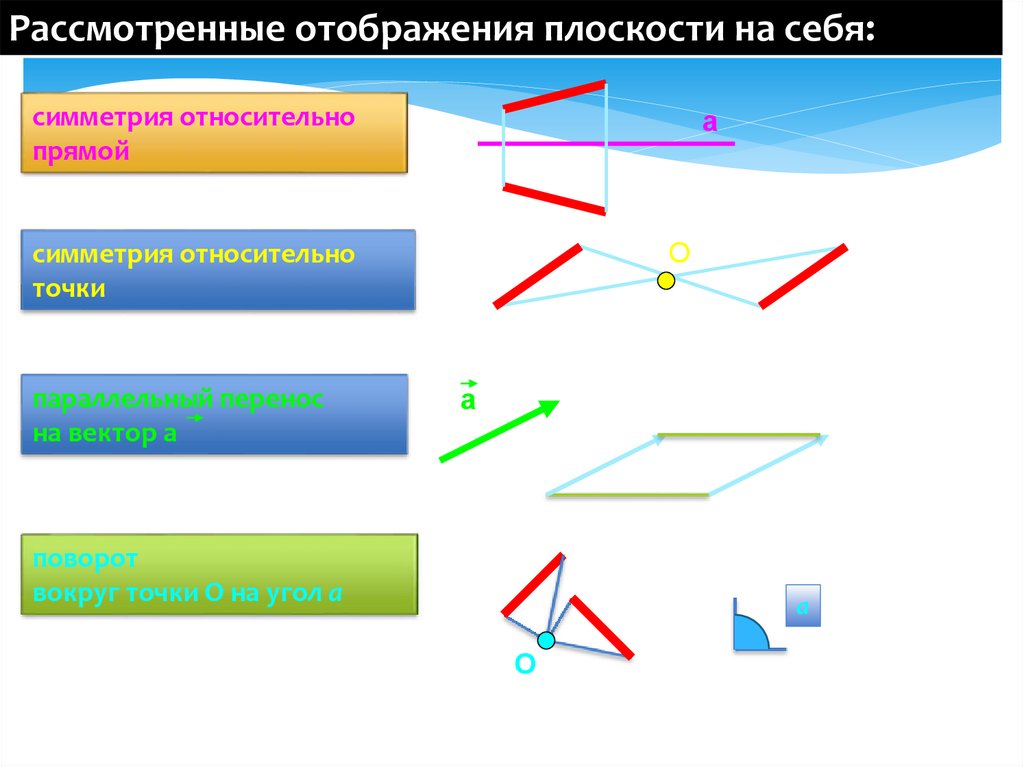
21.
Рассмотренные отображения плоскости на себя:симметрия относительно
прямой
а
О
симметрия относительно
точки
параллельный перенос
на вектор а
а
поворот
вокруг точки О на угол а
а
О
являются движениями.














 mathematics
mathematics








