Similar presentations:
System of linear equations. Lecture 4-5
1. System of linear equations
SYSTEM OF LINEAREQUATIONS
K A R A S H B AY E VA Z H . O .
SENIOR-LECTURER
2. overview
OVERVIEW• Rank of a matrix
• Systems of linear equations
• Matrix representation of SLEs and solution.
• Elementary row and column operations
3. Rank of A Matrix
RANK OF A MATRIX• A matrix of r rows and c columns is said to be of
order r by c. If it is a square matrix, r by r, then the
matrix is of order r.
• The rank of a matrix equals the order of highest-order
nonsingular submatrix.
• Nonsingular matrices have non-zero determinants
• Singular matrices have zero determinants
2- 3
4.
5. Computing rank by various methods
COMPUTING RANK BY VARIOUSMETHODS
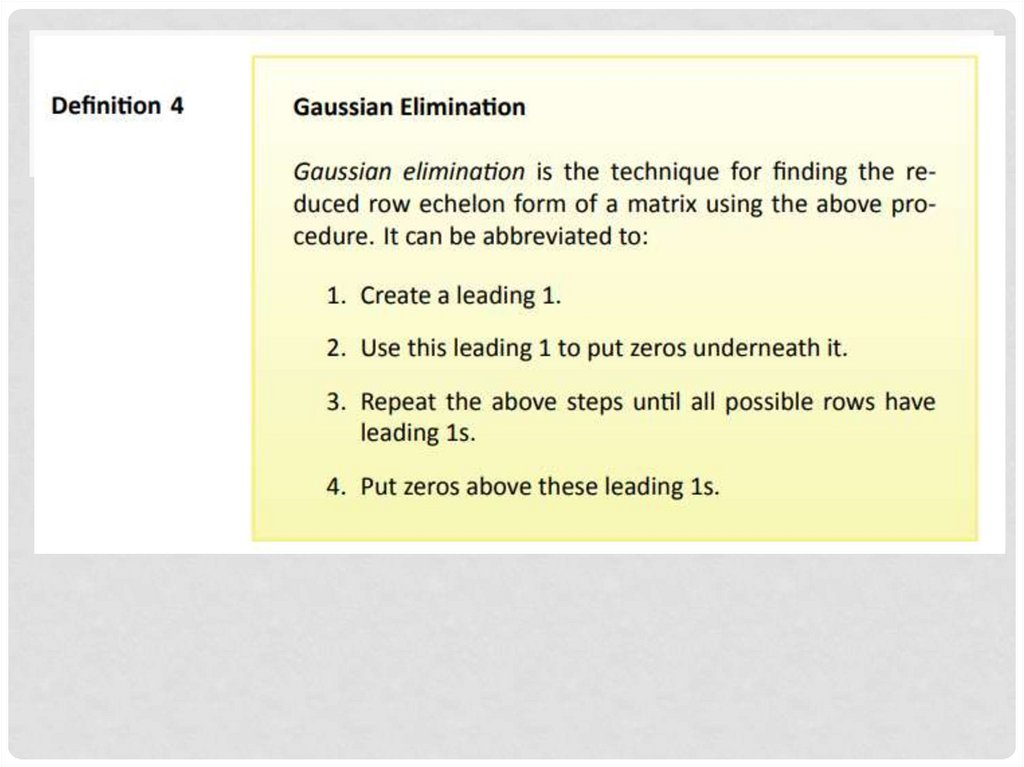
• By Gauss elimination
• By determinants
• By minors
6.
7. Elementary row and column operations
ELEMENTARY ROW AND COLUMN OPERATIONS8. Elementary row and column operations
ELEMENTARY ROW AND COLUMN OPERATIONS9.
10.
11.
12. Example 1: Rank of Matrix
EXAMPLE 1: RANK OF MATRIX2 3 order matrix,
1 2 4
R
2
4
8
3 square submatrices:
1 2
1 4
R1
, R2
,
2 4
2 8
2 4
R3
4
8
Each of these has a determinant of 0, so the rank is less than 2.
Thus the rank of R is 1.
2- 12
13. Example 2: Rank of Matrix
EXAMPLE 2: RANK OF MATRIX2
A 1
9
4
3
10
6
5
11
Since |A|=0, the rank is not 3. The following
submatrix has a nonzero determinant:
2 4
2(3) 4(1) 2
1 3
Thus, the rank of A is 2.
2- 13
14. Systems of linear equations
SYSTEMS OF LINEAR EQUATIONS15.
MATRIX REPRESENTATION OF SLES• Any SLEs can be formulated in the matrix form:
16. Methods of solving SLE
METHODS OF SOLVING SLE17. Methods of solving SLE
METHODS OF SOLVING SLE18. Gauss elimination
GAUSS ELIMINATION• Two steps
• 1. Forward Elimination
• 2. Back Substitution
19. Forward Elimination
FORWARD ELIMINATIONA set of n equations and n unknowns
a11x1 a12 x2 a13 x3 ... a1n xn b1
a21x1 a22 x2 a23 x3 ... a2n xn b2
.
.
.
.
.
.
an1x1 an 2 x2 an3 x3 ... ann xn bn
(n-1) steps of forward elimination
20. Forward Elimination
FORWARD ELIMINATIONStep 1
For Equation 2, divide Equation 1 by a11 and
multiply by a21 .
a21
a (a11x1 a12 x2 a13 x3 ... a1n xn b1 )
11
a21
a21
a21
a21x1
a12 x2 ...
a1n xn
b1
a11
a11
a11
21. Forward Elimination
FORWARD ELIMINATIONSubtract the result from Equation 2.
a21x1 a22 x2 a23 x3 ... a2n xn b2
a21
a21
a21
− a21x1 a a12 x2 ... a a1n xn a b1
11
11
11
_________________________________________________
a21
a21
a21
a22
a12 x2 ... a2 n
a1n xn b2
b1
a11
a11
a11
or
a x ... a x b
'
22 2
'
2n n
'
2
22. Forward Elimination
FORWARD ELIMINATIONRepeat this procedure for the remaining
equations to reduce the set of equations as
a11x1 a12 x2 a13 x3 ... a1n xn b1
'
'
a22
x2 a23
x3 ... a2' n xn b2'
'
'
a32
x2 a33
x3 ... a3' n xn b3'
.
.
.
.
.
.
.
.
.
'
an' 2 x2 an' 3 x3 ... ann
xn bn'
End of Step 1
23. Forward Elimination
FORWARD ELIMINATIONStep 2
Repeat the same procedure for the 3rd term of
Equation 3.
a11x1 a12 x2 a13 x3 ... a1n xn b1
'
'
a22
x2 a23
x3 ... a2' n xn b2'
"
a33
x3 ... a3" n xn b3"
.
.
.
.
.
.
"
an" 3 x3 ... ann
xn bn"
End of Step 2
24. Forward Elimination
FORWARD ELIMINATIONAt the end of (n-1) Forward Elimination steps, the
system of equations will look like
a11 x1 a12 x2 a13 x3 ... a1n xn b1
'
'
a22
x2 a23
x3 ... a2' n xn b2'
"
a33
x3 ... a3" n xn b3"
.
.
.
.
.
.
n 1
n 1
ann
xn bn
End of Step (n-1)
25. Matrix Form at End of Forward Elimination
MATRIX FORM AT END OFFORWARD ELIMINATION
a11 a12
0 a'
22
0
0
0
0
a13
'
a23
a"33
0
a1n x1 b1
'
'
a 2 n x2
b2
a"3n x3 b3"
(n 1 )
xn bn(n-1 )
0 ann
26. Back Substitution Starting Eqns
BACK SUBSTITUTION STARTING EQNSa11 x1 a12 x2 a13 x3 ... a1n xn b1
'
'
a22
x2 a23
x3 ... a2' n xn b2'
"
a33
x3 ... an" xn b3"
.
.
.
n 1
.
.
.
n 1
ann xn bn
27. Back Substitution
BACK SUBSTITUTIONStart with the last equation because it has only one unknown
( n 1)
n
( n 1)
nn
b
xn
a
28. Back Substitution
BACK SUBSTITUTION( n 1)
n
( n 1)
nn
b
xn
a
xi
bi i 1 ai ,ii 11 xi 1 ai ,ii 12 xi 2 ... ai ,in 1 xn
i 1
aii
i 1
xi
bi
aij i 1 x j
n
j i 1
i 1
ii
a
for i n 1,...,1
for i n 1,...,1

































 mathematics
mathematics








