Ex: Find the determinants of the following triangular matrices

712.13K

Category: $mathematics$ mathematics

Determinants

1. Determinants

2.

1 The Determinant of a Matrix
2 Properties of Determinants
3 Application of Determinants: Cramer’s Rule
3.2

4.

Determinant - a square array of
numbers or variables enclosed between
parallel vertical bars.
**To find a determinant you must have
a SQUARE MATRIX!!**
Finding a 2 x 2 determinant:
a
b
c d
= ad - bc

Given a square matrix A its determinant is a real number
associated with the matrix.
The determinant of A is written:
det (A)
or
|A|
For a 2x2 matrix, the definition is
a
b
a
b
det
=
= ad - bc
c d
c d
• For larger matrices the definition is more
complicated

6.

※ The determinant is NOT a matrix operation
※ The determinant is a kind of information extracted from a
square matrix to reflect some characteristics of that square
matrix
※ For example, this chapter will discuss that matrices with a
zero determinant are with very different characteristics from
those with non-zero determinants
※ The motives to calculate determinants are to identify the
characteristics of matrices and thus facilitate the comparison
between matrices since it is impossible to investigate or
compare matrices entry by entry
※ The similar idea is to compare groups of numbers through
the calculation of averages and standard deviations
※ Not only the determinant but also the eigenvalues and
eigenvectors are the information that can be used to identify
the characteristics of square matrices
3.6

7.

The determinant of a 2 × 2 matrix:
a11 a12
A
a
a
21 22
det( A) | A | a11a22
a21a12
Note:
1. For every SQUARE matrix, there is a real number
associated with this matrix and called its determinant
2. It is common practice to omit the matrix brackets
a11 a12
a11 a12
a
a 21 a 22
21 a22
3.7

8.

Historically speaking, the use of determinants arose from the
recognition of special patterns that occur in the solutions of
linear systems:
a11 x1
a21 x1
a12 x2
b1
a22 x2
b2
b1a22 b2 a12
b2 a11 b1a21
x1
and x2
a11a22 a21a12
a11a22 a21a12
Note:
1. x1 and x2 have the same denominator, and this quantity is
called the determinant of the coefficient matrix A
2. There is a unique solution if a11a22 – a21a12 = |A| ≠ 0
3.8

9. Determinants 2x2 examples

1
2
det
3 4
1
2
=
3 4
= (1)(4) – (2)(3) = -2
-5
2
det
-2 0
-5
2
=
-2 0
= (-5)(0) – (2)(-2) = 4
1
2
det
2 4
1
2
=
2 4
= (1)(4) – (2)(2) = 0
Note: The determinant of a matrix can be positive, zero, or negative

10.

Determinants
• To define det(A) for larger matrices, we will
need the definition of a minor Mij
• The minor Mij of a matrix A is the matrix
formed by removing the ith row and the jth
column of A
1 1 -2
A = -1 2 3
2 7 0
M11 : remove row 1, col 1
2
3
M11 =
7 0

11.

12.

13.

14.

15.

16.

17.

18.

19.

The formula for a 3x3 matrix
For a matrix
a11 a12 a13
A = a21 a22 a23
a31 a32 a33
• Its determinant is given by
|A| = a11|M11| - a12|M12| + a13|M13|
• From the formula for a 2x2 matrix:
a22 a23
|M11|=
= a22a33 - a23a32
a32 a33

20.

The formula for a 3x3 matrix
For a matrix
a11 a12 a13
A = a21 a22 a23
a31 a32 a33
• Its determinant is given by
|A| = a11|M11| - a12|M12| + a13|M13|
• From the formula for a 2x2 matrix:
a21 a23
|M12|=
= a21a33 - a23a31
a31 a33

21.

22.

3x3 Example
1 1 -2
A = -1 2 3
2 7 0
|A| = 1x|M11| - 1x|M12| + (-2)x|M13|
2
3
|A|= 1x
7 0
-1
3
- 1x
2 0
-1
2
+ (-2)
2 7
= 1x(-21) -1x(-6) +(-2)x(-11) = 7

23.

3x3 Example
0 1 3
B= 5 3 1
-1 2 0
|B| = 0x|M11| - 1x|M12| + 3x|M13|
3
1
|B|= 0x
2 0
5
1
- 1x
-1 0
= 0x(-2) -1x(1) +(3)x(13) = 38
5
3
+ 3x
-1 2

24.

The formula for a 3x3 matrix
For the matrix
a11 a12 a13
A = a21 a22 a23
a31 a32 a33
• We used the top row to calculate the determinant:
|A| = a11|M11| - a12|M12| + a13|M13|
• However, we could equally have used any row of
the matrix and performed a similar calculation

25.

The formula for a 3x3 matrix
For the matrix
a11 a12 a13
A = a21 a22 a23
a31 a32 a33
• Using the top row:
|A| = a11|M11| - a12|M12| + a13|M13|
• Using the second row
|A| = -a21|M21| + a22|M22| - a23|M23|
• Using the third row
|A| = a31|M31| - a32|M32| + a33|M33|

26.

The formula for a 3x3 matrix
|A| = a11|M11| - a12|M12| + a13|M13|
= -a21|M21| + a22|M22| - a23|M23|
= a31|M31| - a32|M32| + a33|M33|
• Notice the changing signs depending on what
row we use:
+ - +
- + + - +

27.

The formula for a 3x3 matrix
• Equally, we could have used any column as long
as we follow the signs pattern
a11 a12 a13
A = a21 a22 a23
a31 a32 a33
+ - +
- + + - +
• E.g. using the first column:
|A| = a11|M11| - a21|M21| + a31|M31|

28.

• This choice sometimes makes it a bit easier to
calculate determinants. e.g.
1 1 -2
A= 0 2 3
0 1 1
• Using the first row:
2
3
|A|= 1x
1 1
0
3
- 1x
0 1
0
2
+ (-2) x
0 1
= 1x(-1) -1x(0) + (-2)x(0) = -1

29.

• This choice sometimes makes it a bit easier to
calculate determinants. e.g.
1 1 -2
A= 0 2 3
0 1 1
• However, using the first column:
2
3
|A|= 1x
1 1
- 0 + 0 = 1x(-1) = -1

30.

A general formula for determinants
• For a 4x4 matrix we add up minors like the 3x3
case, and again use the same signs pattern
+
+
-
+
+
+
+
-
+
+
• Notice that if we think of the signs pattern as a
matrix, then it can be written as (-1)i+j

31.

A general formula for determinants

32.

3.32

33.

Minor of the entry aij: the determinant of the matrix obtained
by deleting the i-th row and j-th column of A
a11
a12
M ij
a1( j 1)
a1( j 1)
a1n
a( i 1)1
a( i 1)( j 1)
a( i 1)( j 1) a( i 1) n
a( i 1)1
a( i 1)( j 1)
a( i 1)( j 1) a( i 1) n
a n1
an ( j 1)
an ( j 1)
ann
Aij ( 1) i j M ij
3.33

34.

Ex:
a11
A a21
a31
M 21
a32
a13
a23
a33
a12
a13
a32
a33
a12
a22
A21 ( 1) 2 1 M 21 M 21
M 22
a13
a31
a33
А22 ( 1) 2 2 M 22 M 22
Notes: Sign pattern for cofactors. Odd
positions (where i+j is odd) have negative
signs, and even positions (where i+j is even)
have positive signs. (Positive and negative
signs appear alternately at neighboring
positions.)
a11
3.34

35.

Theorem: Expansion by cofactors
Let A be a square matrix of order n, then the determinant of A
is given by
n
(a) det( A) | A | aij Aij ai1 Ai1 ai 2 Ai 2
j 1
ain Ain
(cofactor expansion along the i-th row, i=1, 2,…, n)
or
n
(b) det( A) | A | aij Aij a1 j A1 j a2 j A2 j
i 1
anj Anj
(cofactor expansion along the j-th column, j=1, 2,…, n)
※The determinant can be derived by performing the cofactor expansion
along any row or column of the examined matrix
3.35

36.

Ex: The determinant of a square matrix of order 3
a11
A a21
a31
a12
a22
a32
a13
a23
a33
det( A) a11 A11 a12 A12 a13 A13 (first row expansion)
a21 A21 a22 A22 a23 A23 (second row expansion)
a31 A31 a32 A32 a33 A33 (third row expansion)
a11 A11 a21 A21 a31 A31 (first column expansion)
a12 A12 a22 A22 a32 A32 (second column expansion)
a13 A13 a23 A23 a33 A33 (third column expansion)
3.36

37.

Ex: The determinant of a square matrix of order 3
0 2 1
A 3 1 2
4 0 1
Sol:
1 1
A11 ( 1)
1 2
0
1 3
A13 ( 1)
1
det( A) ?
1
3 1
4
0
1 2
A12 ( 1)
3 2
4 1
( 1)( 5) 5
4
det( A) a11 A11 a12 A12 a13 A13
(0)( 1) (2)(5) (1)(4)
14
3.37

38.

Ex: The determinant of a square matrix of order 4
1 2
1 1
A
0
2
4
3
0
0 2
det( A) ?
0 3
0 2
3
3.38

39.

Sol:
det( A) (3)( A13 ) (0)( A23 ) (0)( A33 ) (0)( A43 ) 3 A13
1 1
3( 1)1 3 0
3
2
2
3
4 2
2
2
2 1 1
2 2 1
2 3 1 1
3 (0)( 1)
( 2)( 1)
(3)( 1)
4
2
3
2
3
4
3 0 (2)(1)( 4) (3)( 1)( 7)
(3)(13)
39
※ By comparing the exercises, it is apparent that the computational effort for the
determinant of 4×4 matrices is much higher than that of 3×3 matrices.
3.39

40.

Upper triangular matrix:
All entries below the main diagonal are zeros
Lower triangular matrix:
All entries above the main diagonal are zeros
Diagonal matrix:
All entries above and below the main diagonal are zeros
Ex:
a11 a12 a13
0 a22 a23
0 0 a
33
a11 0 0
a21 a22 0
a a a
31 32 33
a11 0 0
0 a22 0
0 0 a
33
upper triangular
lower triangular
diagonal
3.40

41.

Theorem: (Determinant of a Triangular Matrix)
If A is an n n triangular matrix (upper triangular, lower
triangular, or diagonal), then its determinant is the product of
the entries on the main diagonal. That is
det( A) | A | a11a22 a33 ann
3.41

42. Ex: Find the determinants of the following triangular matrices

0
2
4 2
(a) A
5 6
1
5
0 0
0 0
1 0
3 3
Sol:
1
0
(b) B 0
0
0
0 0 0
3 0 0
0 2 0
0 0 4
0 0 0
0
0
0
0
2
(a) |A| = (2)(–2)(1)(3) = –12
(b) |B| = (–1)(3)(2)(4)(–2) = 48
3.42

43. 2 Properties of Determinants

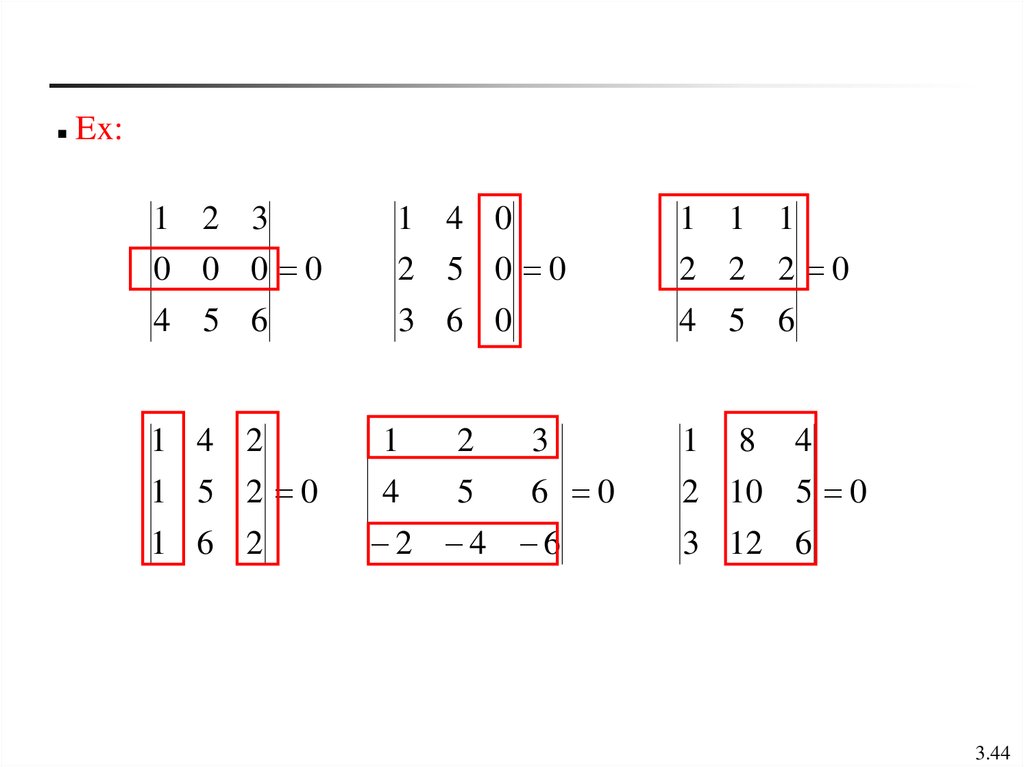
Conditions that yield a zero determinant
If A is a square matrix and any of the following conditions is
true, then det(A) = 0
(a) An entire row (or an entire column) consists of zeros
(b) Two rows (or two columns) are equal
(c) One row (or column) is a multiple of another row (or column)
3.43

44.

Ex:
1 2 3
1 4 0
1 1 1
0 0 0 0
2 5 0 0
2 2 2 0
4 5 6
3 6 0
4 5 6
1 4 2
1
2
3
1
1 5 2 0
4
5
6 0
2 10 5 0
1 6 2
2 4 6
8
4
3 12 6
3.44

45.

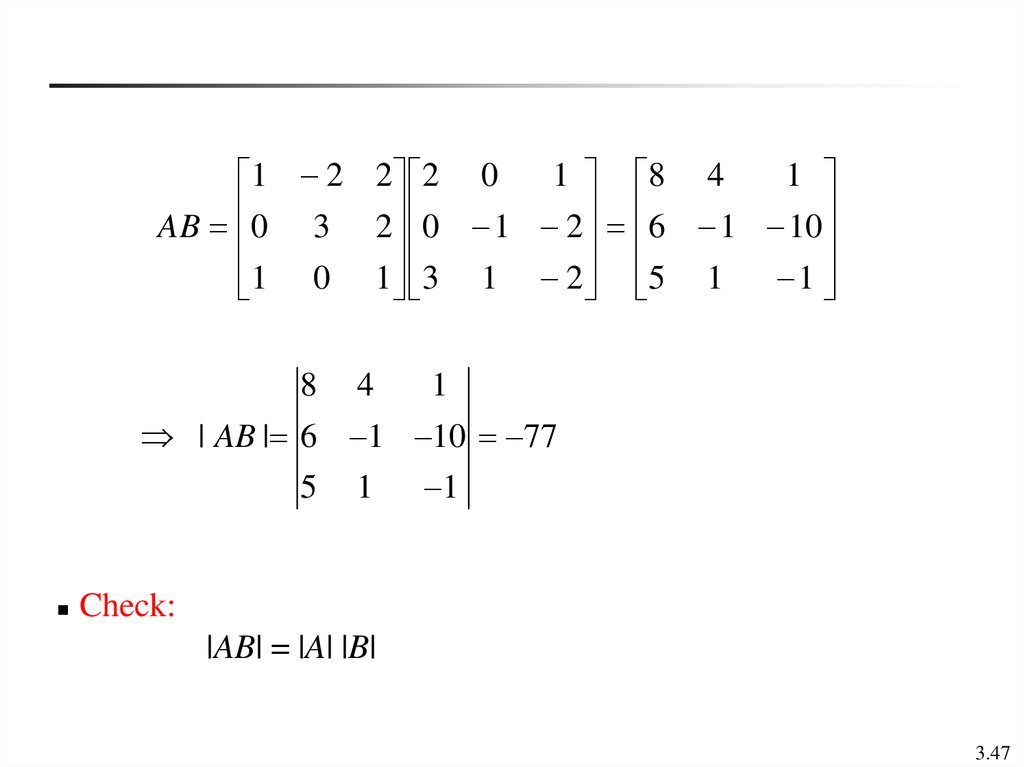
Theorem: Determinant of a matrix product
det(AB) = det(A) det(B)
Notes:
(1) det( A1 A2
(Verified by Ex on the next slide)
(2)
An ) det( A1 ) det( A2 )
det( An )
det( A B) det( A) det( B)
a11
a12
a13
a11
a12
a13
a11
a12
a13
(3) a21 b21 a22 b22 a23 b23 a21 a22 a23 b21 b22 b23
a31
a32
a33
a31
a32
a33
a31
a32
a33
3.45

46.

Ex 1: The determinant of a matrix product
1 2 2
A 0 3 2
1 0 1
1
2 0
B 0 1 2
3 1 2
Find |A|, |B|, and |AB|
Sol:
1 2 2
| A | 0
3
2 7
1
0
1
2
0
1
| B | 0 1 2 11
3
1
2
3.46

47.

1 8 4
1
1 2 2 2 0
AB 0 3 2 0 1 2 6 1 10
1 0 1 3 1 2 5 1
1
8
4
1
| AB | 6 1 10 77
5
1
1
Check:
|AB| = |A| |B|
3.47

48.

Theorem: Determinant of a scalar multiple of a matrix
If A is an n × n matrix and c is a scalar, then
det(cA) = cn det(A)
Ex 2:
(can be proven by repeatedly use the fact
that
)
if B M i( k ) ( A) B k A
1 2 4
10 20 40
A 30
0 50 , if 3 0 5 5, find |A|
20 30 10
2 3 1
Sol:
1 2 4
1 2 4
3
0 5 (1000)(5) 5000
A 10 3
0 5 A 10 3
2 3 1
2 3 1
3.48

49.

Theorem: (Determinant of an invertible matrix)
A square matrix A is invertible (nonsingular) if and
only if det(A) 0
3.49

50.

Ex 3: Classifying square matrices as singular or nonsingular
0 2 1
A 3 2 1
3 2 1
0 2 1
B 3 2 1
3 2
1
Sol:
A 0
A has no inverse (it is singular)
B 12 0
B has inverse (it is nonsingular)
3.50

51. Inverse Matrices

3.51

52. Theorem of Inverse Matrices

3.52

53.

3.53

54.

3.54

55.

3.55

56. Example 3

3.56

57.

3.57

58.

Theorem: Determinant of an inverse matrix
1
If A is invertible, then det( A )
det( A)
1
Theorem: Determinant of a transpose
If A is a square matrix, then det( AT ) det(A)
Ex 4:
Sol:
1 0 3
A 0 1 2
2 1 0
1
0
3
| A | 0 1 2 4
2
1
0
1
(a) A ?
(b)
AT ?
1 1
A 4
AT A 4
A 1
3.58

59.

The similarity between the noninvertible matrix and the real
number 0
Matrix A
Invertible
det( A) 0
A 1 exists and det( A 1 )
Noninvertible
Real number c
c 0
1
det( A)
c 1 exists and c 1 =
det( A) 0
c 0
A 1 does not exist
c 1 does not exist
1
1
1
det( A )
det(
A
)
0
1 1 1
c = =
c 0
1
c
3.59

60.

Equivalent conditions for a nonsingular matrix:
If A is an n × n matrix, then the following statements are
equivalent
(1) A is invertible
(2) Ax = b has a unique solution for every n × 1 matrix b
(3) Ax = 0 has only the trivial solution
(4) det(A) 0
3.60

61.

Ex 5: Which of the following system has a unique solution?
2 x2
x3
1
3x1
2 x2
x3
4
3x1
2 x2
x3
4
2 x2
x3
1
3x1
2 x2
x3
4
3x1
2 x2
x3
4
(a)
(b)
3.61

62.

Sol:
(a) Ax b (the coefficient matrix is the matrix A in Ex 3)
A 0 (from Ex 3)
This system does not have a unique solution
(b) Bx b (the coefficient matrix is the matrix B in Ex 3)
B 12 0 (from Ex 3)
This system has a unique solution
3.62

63. 3 Applications of Determinants

Theorem: Cramer’s Rule
a11 x1 a12 x2
a1n xn b1
a21 x1 a22 x2
a2 n xn b2
an1 x1 an 2 x2
ann xn bn
where A aij
n n
A(1) A(2)
Ax b
A(i) represents the i-th
column vector in A
b1
x1
b
x
2
2
( n)
b
x
,
A ,
x
bn
n
Suppose this system has a unique solution, i.e.,
det( A)
a11
a12
a1n
a21
a22
a2 n
an1
an 2
ann
0
3.63

64.

By defining Aj A(1) A(2)
a11
a
21
an1
A( j 1) b A( j 1)
a1( j 1)
b1
a1( j 1)
a2( j 1)
b2
a2( j 1)
an ( j 1)
bn
an ( j 1)
(i.e., det( Aj ) b1C1 j b2C2 j
xj
det( Aj )
det( A)
, j 1, 2,
A( n )
a1n
a2 n
ann
bnCnj )
,n
3.64

65.

Ex: Use Cramer’s rule to solve the system of linear equation
x 2 y 3z 1
2x
z 0
3x 4 y 4 z 2
Sol:
1 2 3
1 2 3
det( A1 ) 0 0
1 8
det( A) 2
0
1 10
2 4 4
3 4 4
1
1 1 3
det( A2 ) 2
0
1 15,
3
2
4
det( A1 ) 4
x
det( A) 5
det( A3 ) 2
det( A2 ) 3
y
det( A)
2
3
2
1
0
0 16
4 2
det( A3 ) 8
z
det( A)
5
3.65

66. Keywords

determinant
minor
cofactor
expansion by cofactors
upper triangular matrix
lower triangular matrix
diagonal matrix
Cramer’s rule
3.66

English Русский Rules