Similar presentations:
Кинематика
1. 2. КИНЕМАТИКА.
1. Предмет кинематики.Кинематика изучает механическое движение без учета сил.
Кинематика разделяется на кинематику мочки и кинематику
твердого тела.
2. Кинематика точки.
2.1. Д в а с п о с о б а з а д а н и я д в и ж е н и я т о ч к и :
векторно-координатный и естественный.
При в е к т о р н о - к о о р д и н а т н о м способе задаются
либо три координаты точки для любого момента времени:
x=x(t), y=y(t), z=z(t),
(2.1)
либоy радиус-вектор точки,
r имеющий,
xi y j zкак
k , правило, начало в (2.2
начале системы координат:
)
где
i
,
j
,
k
единичные
орты
координатных
A
x
o
осей.
r
z
2. 2. Кинематика точки (продолжение).
При е с т е с т в е н н о м с п о с о б е задается закон движенияточки
S=S(t) и уравнение траектории f(x,y,z).
y
Движение точки считается
заданным, если можно в каждый
момент времени определить ее
положение на траектории.
S(t)
o
f(x,y,z)
z
x
2.2. С к о р о с т ь точки характеризует быстроту перемещения
точки в пространстве.
Средняя
с к о р о с т ь.
y
Средняя скорость (рис.2.1)
определяется выражением:
r
r (t )
r (t t )
j
z
k
i
Рис.2.1.
vср
r
.
t
x
Слайд 25
3. 2. Кинематика точки (продолжение).
М г н о в е н н а я с к о р о с т ь (или просто с к о р о с т ь).Чаще всего определяют мгновенную скорость в данный момент
времени:
r
v lim
t
t 0
d r dx
dy
dz
i
j k.
dt dt
dt
dt
(2.3
)
Обозначим проекции вектора скорости на координатные оси:
x
vx x ,
t
y
vy y ,
t
vz z
z
.
t
(2.4
)
С учетом этих обозначений формула (2.3) примет вид:
v vx i v y j vz k .
(2.5)
Модуль скорости
v vx2 v y2 vz2 .
(2.6
)
Слайд 26
4. 2. Кинематика точки (продолжение).
2.3. У с к о р е н и е точки – это скорость изменения скорости.Среднее
v
.
ускорение аср
t
М г н о в е н н о е ускорение
dv d 2 r d 2x
d2y
d 2z
а
2 2 i 2 j 2 k ax i a y j az k ,
dt dt
dt
dt
dt
(2.7)
где проекции ускорения на координатные оси:
2
d x
ax x 2 ,
dt
d2y
ay y 2 ,
dt
М о д у л ь ускорения (п о л н о е
a ax2 a y2 a z2 .
d 2z
az z 2 .
dt
(2.8)
ускорение):
(2.9
)
Ускорение также разделяется на касательное и нормальное.
Слайд 27
5. 2. Кинематика точки (продолжение).
Определение к а с а т е л ь н о г о и н о р м а л ь н о г оускорений.
Пусть т.М движется по криволинейной
d
траектории. При этом изменяется и величина и
n
направление скорости.
/
a n о dS
M
о
M
a v
/
v
Рис.2.2.
n
/
d
M
v
dv
d vn
v d v
Величину скорости изменяет касательное
an
ускорение
,
a
а направление нормальное ускорение
- рис.2.2
d v
и 2.3. Обозначим приращение
скорости по d vn .
dv
d vn
касательной
2
2
Тогда a ,к aan
. a an a . (2.10
траектории вdtт.М через dt , а по нормали n )через
d v d vn (
Рассмотрим только приращение
=0).
В этом
d v
dv и
d
случае
=0 ,
dv =
d2S
(2.11
a
2 .
)
dt
dt
Рис.2.3.
d vn
d v (
Рассмотрим теперь только приращение
=0). Из
dS
рис.2.3 следует:
d
. C учетом этих выражений
dvn vd , а из рис.2.2:
формула
2
v
(2.10) дляa n
примет an .
(2.12 Слайд28
6. 2. Кинематика точки (продолжение).
2.4. П р о с т ы е ф о р м ыдвижения точки.
а). П р я м о л и н е й н о е движение:
= ,
dv
аn 0, a а
.
dt
б). Р а в н о м е р н о е движение:
v const ,
в). Р а в н о м е р н о е
а 0,
v2
an .
п р я м о л и н е й н о е движение:
, v const , аn 0, а 0.
г). Р а в н о п е р е м е н н о е движение (за равные промежутки
времени скорости изменяются на равные величины):
dv
dv a dt ;
a
const
t
dt
v v v0 dv a t v v0 a t ;
0
dS
v
dS vdt v0 a t dt ;
dt t
t
a t 2
S dS v0 a t dt v0t
.
2
0
0
Слайд 29
7. 2. Кинематика точки (продолжение).
2.5. С л о ж н о е д в и ж е н и е т о ч к и.2.5.1. Понятие о сложном движении точки.
При сложном движении точка одновременно участвует в
нескольких движениях. Например, человек идет по
движущемуся поезду. Поезд можно рассматривать как
подвижную систему координат, а движение человека (примем
его за материальную точку М) относительно поезда –
отно
с и т е л ь н ы м движением. Движение поезда относительно
земли (примем ее за неподвижную) назовем п е р е н о с н ы м
движением относительно неподвижной системы координат.
Таким образом,
т. М одновременно
участвует и в
vпер
vотн
аотн
относительном
движении (имеет
и
) и в переносном
апер
движении (имеет
и
).
Движение, совершаемое т. М по отношению к неподвижной
системе отсчета – это а б с оv л ю тан о
е (или сложное)
абс
абс .
движение. Соответственно в абсолютном движении у т. М:
и
Слайд 30
8. 2. Кинематика точки (продолжение).
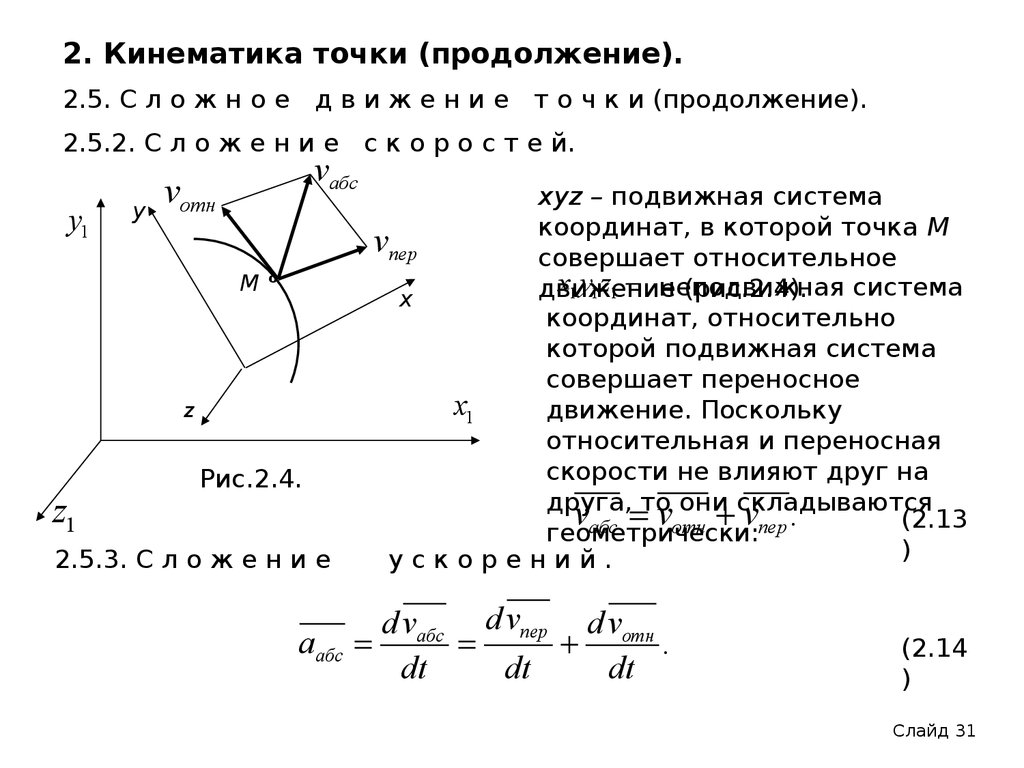
2.5. С л о ж н о е д в и ж е н и е т о ч к и (продолжение).2.5.2. С л о ж е н и е с к о р о с т е й.
y1
y
vабс
vотн
М
о
z
z1
Рис.2.4.
2.5.3. С л о ж е н и е
аабс
xyz – подвижная система
координат, в которой точка М
vпер
совершает относительное
x1 y1 z1 неподвижная
система
движение
(рис.2.4).
x
координат, относительно
которой подвижная система
совершает переносное
x1
движение. Поскольку
относительная и переносная
скорости не влияют друг на
друга, то они складываются
vабс vотн vпер .
(2.13
геометрически:
)
ускорений.
d vабс d vпер d vотн
.
dt
dt
dt
(2.14
)
Слайд 31
9. 2. Кинематика точки (продолжение).
2.5.3. С л о ж е н и еу с к о р е н и й (продолжение).
Скорости изменяются и в переносном и в относительном
движениях. Условимся изменение скорости в относительном
движении отмечать индексом «1», а в переносном – индексом «2».
Формула (2.14) примет
(d vпер )1вид:d vпер 2 (d vотн )1 d vотн 2
(2.15
аабс
.
dt
dt
dt
dt
)
В этой формуле:
аотн
апер
(d vотн )1
dt
dv
акор
пер 2
dt
(d vпер )1
dt
- относительное ускорение; (2.16
)
- переносное ускорение;
dv
отн 2
- кориолисово ускорение.
(2.17)
(2.18)
dt
Кориолисово ускорение характеризует изменение
относительной скорости при переносном движении и изменение
переносной скорости в относительном движении. Таким
образом:
(2.19)
аабс аотн апер акор .
Слайд 32
10. 2. Кинематика точки (продолжение).
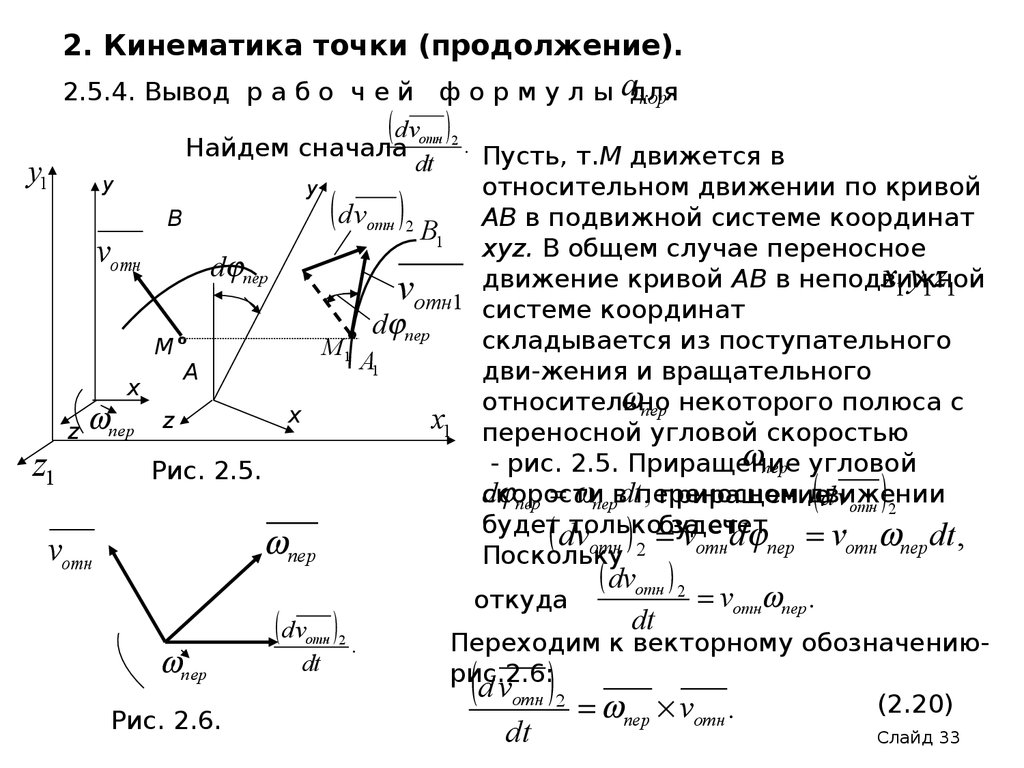
2.5.4. Вывод р а б о ч е й ф о р м у л ы адлякор .
d v
y1
Найдем сначала
отн 2
dt
. Пусть, т.М движется в
относительном движении по кривой
d vотн 2
В
В1 АВ в подвижной системе координат
xyz. В общем случае переносное
vотн
d пер
x1 y1 z1
кривой АВ в неподвижной
vотн1 движение
системе координат
d
о
пер
складывается из поступательного
Мо
М1
А
1
А
дви-жения и вращательного
х
пер некоторого полюса с
относительно
х
x1 переносной угловой скоростью
z пер z
пер угловой
- рис. 2.5. Приращение
z1
Рис. 2.5.
d пер первdtпереносном
, приращение
скорости
движении
d vотн 2
будетdv
только
за
счет
. dt ,
будет
v
d
v
пер
отн 2
отн
пер
отн пер
vотн
Поскольку
у
у
пер
Рис. 2.6.
d v
отн 2
dt
откуда
.
dvотн 2
dt
vотн пер .
Переходим к векторному обозначениюрис.2.6:
d vотн 2
(2.20)
пер vотн .
dt
Cлайд 33
11. 2. Кинематика точки (продолжение).
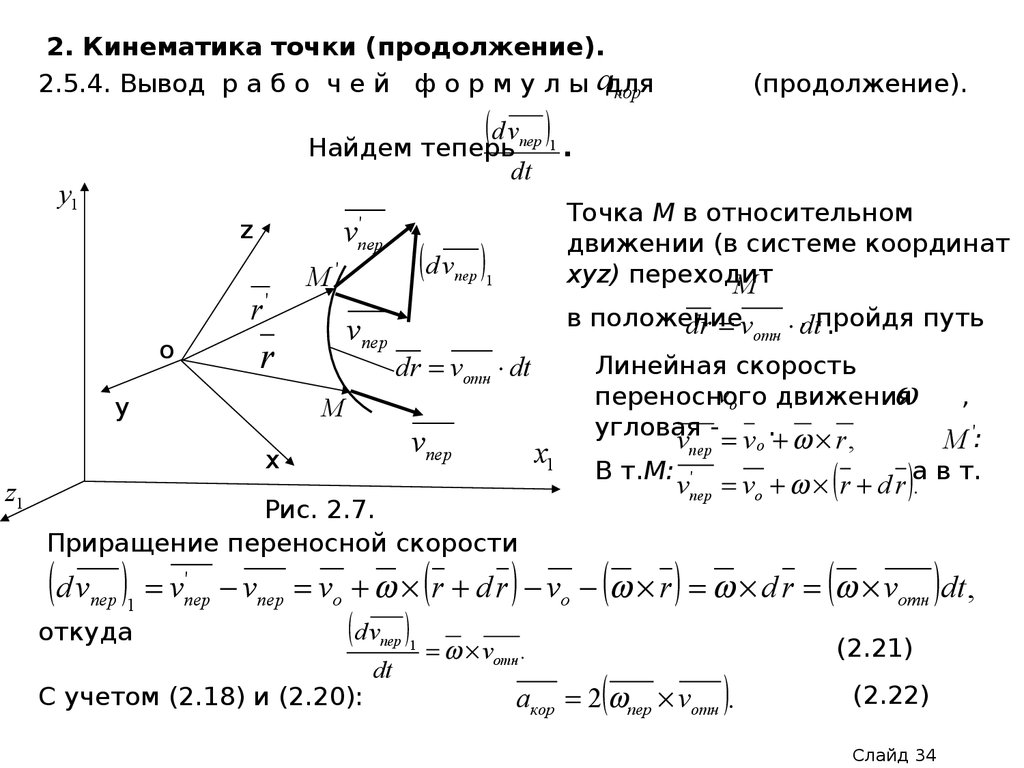
2.5.4. Вывод р а б о ч е й ф о р м у л ы адлякор
dv
Найдем теперь пер 1 .
dt
y1
'
пер
z
v
r'
o
Точка М в относительном
движении (в системе координат
xyz) переходит
M'
d v
M'
пер 1
vпер
r
y
в положение
dr v
отн
dr vотн dt
M
vпер
x
z1
(продолжение).
x1
Рис. 2.7.
Приращение переносной скорости
d v
пер
, пройдя
путь
.
dt
Линейная скорость
vo движения
переносного
угловая .
В т.М:
vпер v o r ,
,
M ':
а в т.
'
vпер
vo r d r .
'
v
пер vпер vo r d r vo r d r vотн dt ,
1
откуда
d v
С учетом (2.18) и (2.20):
пер 1
dt
vотн .
aкор 2 пер vотн .
(2.21)
(2.22)
Слайд 34
12. 2. Кинематика точки (завершение).
перТаким образом, получена рабочая формула
(2.22) для расчета кориолисова ускорения.
Если пер
aкор
=0, то
aкор
=0.
aкор 2 vотн sin ,
Модуль кориолисова ускорения
где
vотн
vотн и
- угол между векторами
.
3. Кинематика твердого тела.
3.1. П р о с т е й ш и е д в и ж е н и я т в е р д о го т е л а.
3.1.1. Поступательное движение.
При поступательном движении тела достаточно знать
движение любой одной
vi const , ai const.
точки тела, поскольку
Частным случаем поступательного движения является равномерное
ai 0.
поступательное движение. В этом случае
Слайд 35
13. 3. Кинематика твердого тела (продолжение)
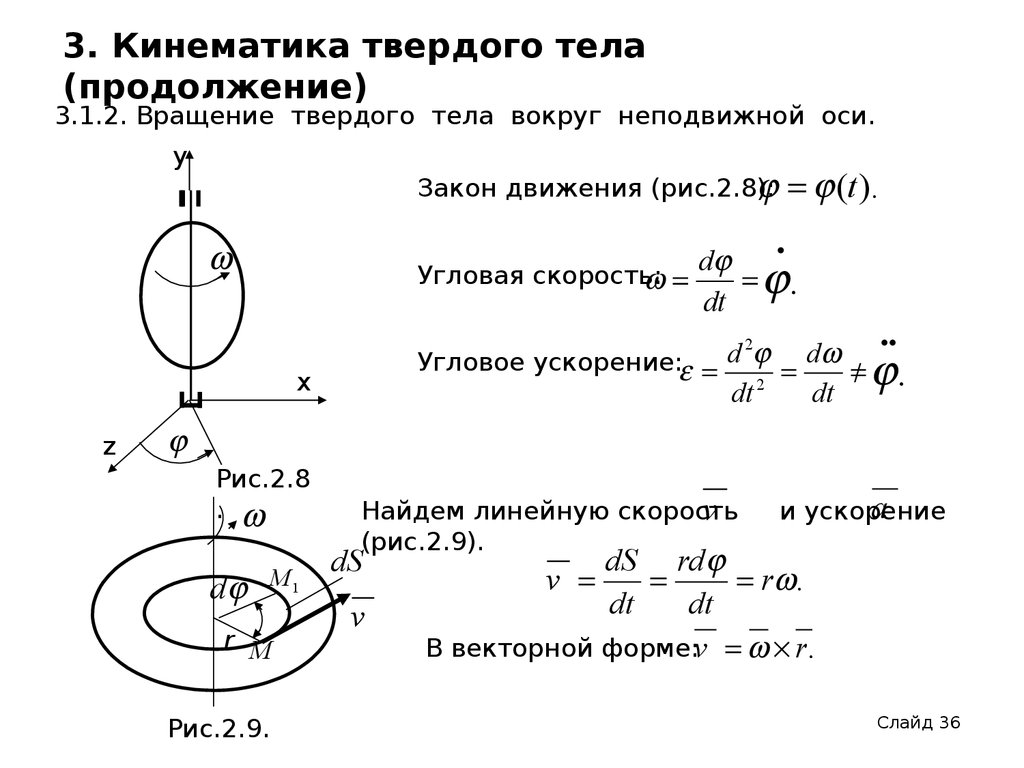
3.1.2. Вращение твердого тела вокруг неподвижной оси.y
Закон движения (рис.2.8):
(t ).
d
Угловая скорость:
.
dt
2
d
Угловое ускорение: d
.
dt 2
dt
x
z
Рис.2.8
.
d
M1
r M
Рис.2.9.
Найдем линейную скорость
v
(рис.2.9).
dS
v
a
и ускорение
dS rd
r .
dt
dt
В векторной форме:v r.
v
Слайд 36
14. 3. Кинематика твердого тела (продолжение)
3.1.2. Вращение твердого тела вокруг неподвижной оси(продолжение).
a a
v.
На рис.2.10 показана эпюра скоростей
an
a
Полное линейное ускорение
касательное
a
S
r
a
a
:
v2
an
2 r.
r
Пример.
x 100t (см); r
Уравнение движения гири
Найти ускорение т.В.
Решение.
2
2
. a B
n
10см.
x 100t
S x r
.
r
r
2
d
d
20t (c 1 ); 2 20(c 2 ).
dt
x
Рис.2.11
и нормальное
an
d v d 2S
a
2 r.
dt
dt
Эпюраv
Рис. 2.10.
разложено на
dt
см
см
2
2
;
a
r
200
;
a
a
a
B
n
.
2
2
с
с
Слайд 37
an 2 r 4000t 2
15. 3. Кинематика твердого тела (продолжение)
3.2. П л о с к о п а р а л л е л ь н о е д в и ж е н и е т в е р д о г от е л а. 3.2.1. Основные понятия.
При плоскопараллельном (плоском)
движении все точки тела перемещаются
параллельно неко-торой фиксированной
у
плоскости П. Достаточно изучить движение
любого сечения, параллельно-го пл. П.
Плоское движение полностью характерих
зуется положением произвольного отрезка
АВ в этом сечении (рис. 2.12).
П
Движение отрезка АВ можно разложить
у
уА
В
А1
В1
А
на пос-тупательное движение полюса А
(произвольная точка на этом отрезке) и
вращательное движе-ние вокруг этого
полюса. Таким образом, движе-ние тела
x Aопределяется
f1 t ; y A fфункциями:
2 t ; f 3 t ,
полностью
В
2
А2
хА
Рис. 2.12.
х
т.е. надо знать v A , a A , , .
За полюс принимается точка, скорость
которой либо известна, либо ее легко
найти.
Слайд 38
16. 3. Кинематика твердого тела (продолжение)
3.2. П л о с к о п а р а л л е л ь н о еела
(п р о д о л ж е н и е).
движение твердого т
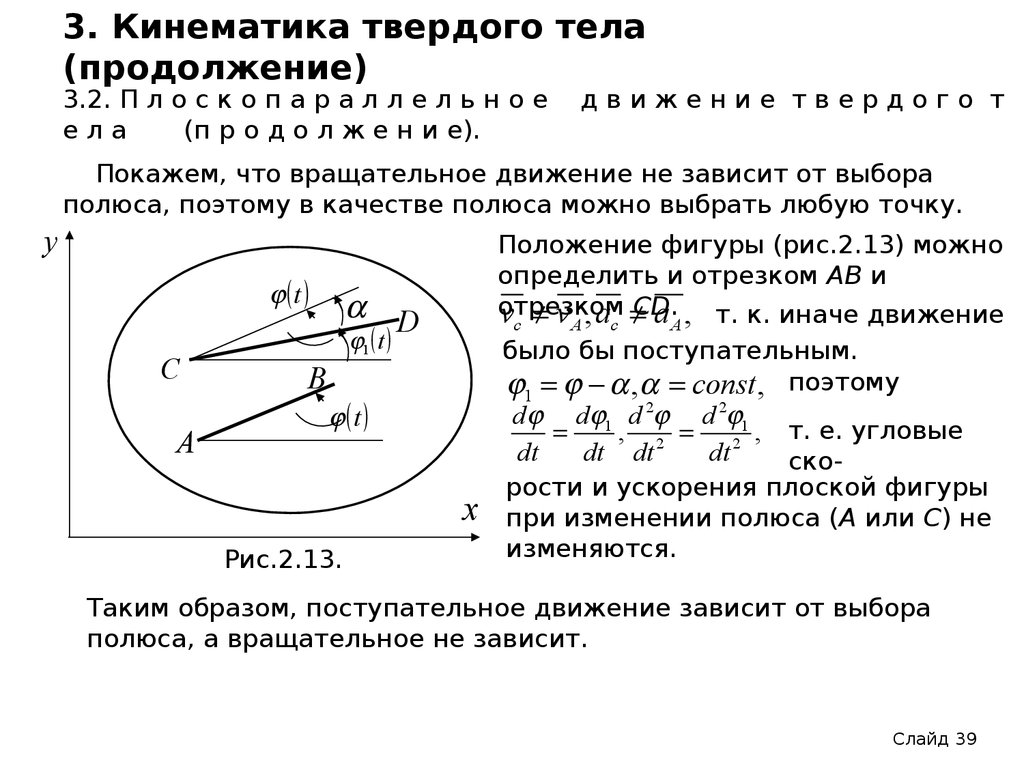
Покажем, что вращательное движение не зависит от выбора
полюса, поэтому в качестве полюса можно выбрать любую точку.
y
t
C
A
Положение фигуры (рис.2.13) можно
определить и отрезком АВ и
отрезком
v v , a СD.
a , т. к. иначе движение
D
c
1 t
B
t
x
Рис.2.13.
A
c
A
было бы поступательным.
1 , const , поэтому
d d 1 d 2 d 2 1
,
2 , т. е. угловые
dt
dt dt 2
dt
скорости и ускорения плоской фигуры
при изменении полюса (А или С) не
изменяются.
Таким образом, поступательное движение зависит от выбора
полюса, а вращательное не зависит.
Слайд 39
17. 3. Кинематика твердого тела (продолжение)
3.2. П л о с к о п а р а л л е л ь н о е д в и ж е н и е т в е р д о го тела
(п р о д о л ж е н и е).
3.2.2. Определение скоростей точек плоской фигуры (рис. 2.14).
vМ
vМA
М
Aо
vA
о
vA
А – полюс,
vМ v А vMA .
vMA AM .
Рис.2.1
4.
3.2.3. Мгновенный
центр скоростей (м.ц.с.).
М.ц.с. – это точка, в которой в данный момент времени
vА
скорость равна нулю. Если тело имеет вращательное
Bо
A
движение, то такая точка существует и она
о
единственная, т.к. в противном случае в различных
vВ точках тела направление скоростей было бы неопрео
Р
деленным. Для определения м.ц.с. (т.Р – рис.2.15) надо
знать скорости двух точек тела, провести к ним
Рис.2.1
и на их пересечении будет м.ц.с. Р.
5. vВ
vперпендикуляры
А
Если скорости в двух точках параллельны, то
положение м.ц.с. находится, как показано на
о
о
A
Ро
B
Слайд 40
Рис.2.16. рис.2.16.
18. 3. Кинематика твердого тела (продолжение)
. 3.2. П л о с к о п а р а л л е л ь н о е д в и ж е н и е т в е р д ого тела
(п р о д о л ж е н и е).
3.2.2 Определение скоростей точек плоской фигуры
(продолжение).
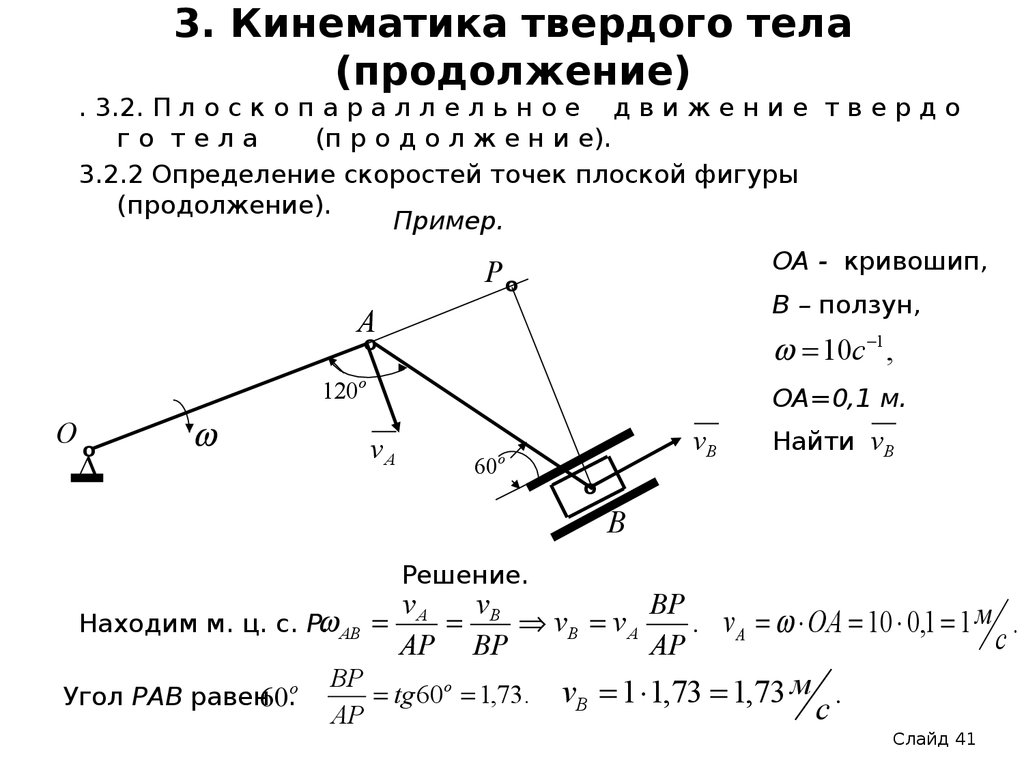
Пример.
ОА - кривошип,
Ро
В – ползун,
A
10с 1 ,
о
120о
Оо
ОА=0,1 м.
vА
60
vВ
о
Найти vВ
о
B
Решение.
Находим м. ц. с. Р. АВ
Угол РАВ равен60.о
vА
vB
BP
vB v A
. v A OA 10 0,1 1 м .
с
AP BP
AP
BP
tg 60o 1,73.
AP
vB 1 1,73 1,73 м .
с
Слайд 41
19. 3. Кинематика твердого тела (продолжение)
3.2. П л о с к о п а р а л л е л ь н о е д в и ж е н и е т в е р д о го тела
(п р о д о л ж е н и е).
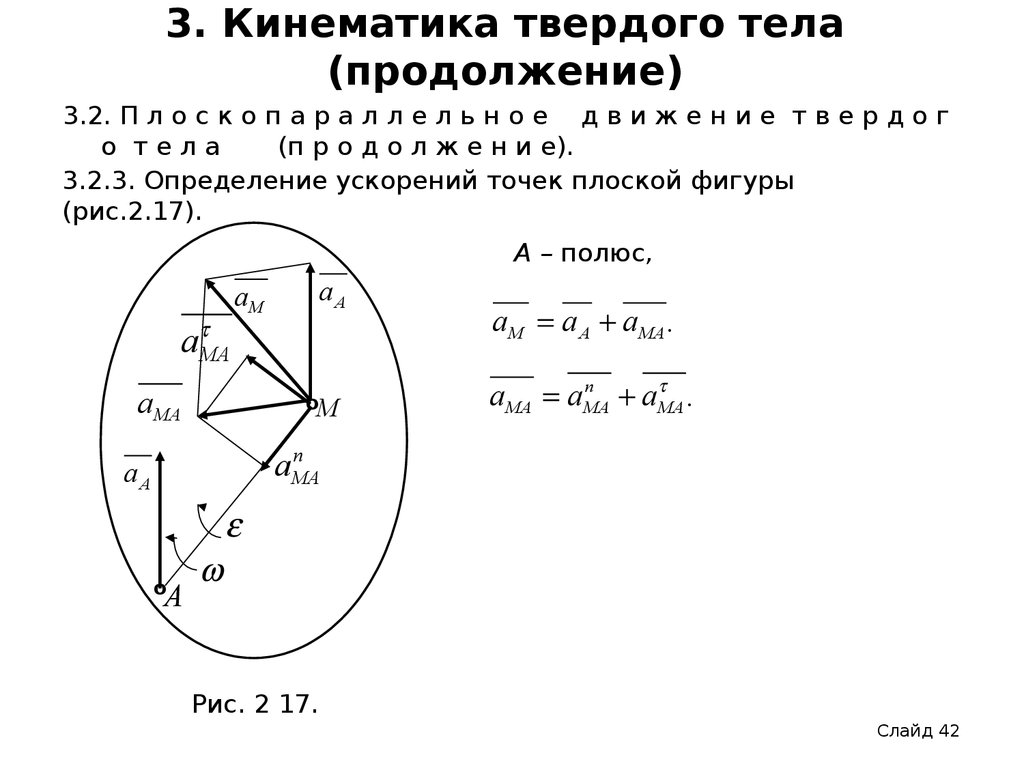
3.2.3. Определение ускорений точек плоской фигуры
(рис.2.17).
А – полюс,
а МА
аА
аM
аMA
оМ
аM а А аМА .
n
аMА аМА
a MA .
n
аМА
аА
о
A
Рис. 2 17.
Слайд 42
20. 3. Кинематика твердого тела (продолжение)
3.2.3 Определение ускорений точек плоской фигуры (продолжение).Пример
r
4о
О
vO
aO
о2
о
1
a
Т .1
о
оТ .2
2
a
Т .3о
n
3
a
Т .4о
,
r 0,5 м.
Найти ускорения точек 1,2,3,4.
Решение
a
3
vo
1
1 o
6c 2 .
2c ,
Т.1 – м.ц.с.
r 0,5
r 0,5
aion 2 r 2 м с 2 .
io
ai аo a a , где
n
2
с
2
Примем за полюс т.О, тогда
n
io
a1
аo 3 м
vo 1 м ,
с
о3
a1n
a1
aO
aO
3
аo a
a 4
аo a4n
a2
a3
a4
a
o
a1
a
2
n 2
1
a a a
a a a
o
n 2
2
2
2
o
2
3
n 2
3
a
o
a
a1n 2 м с 2 .
a
n 2
4
aio r 3 м с 2 .
3 2 2 32
3,16 м с 2 .
6,32 м с 2 .
2
4
5,83 м с 2 .
Слайд 43
21. 3. Кинематика твердого тела (продолжение)
3.2. П л о с к о п а р а л л е л ь н о е д в и ж е н и е т в е р д о г отела
(п р о д о л ж е н и е).
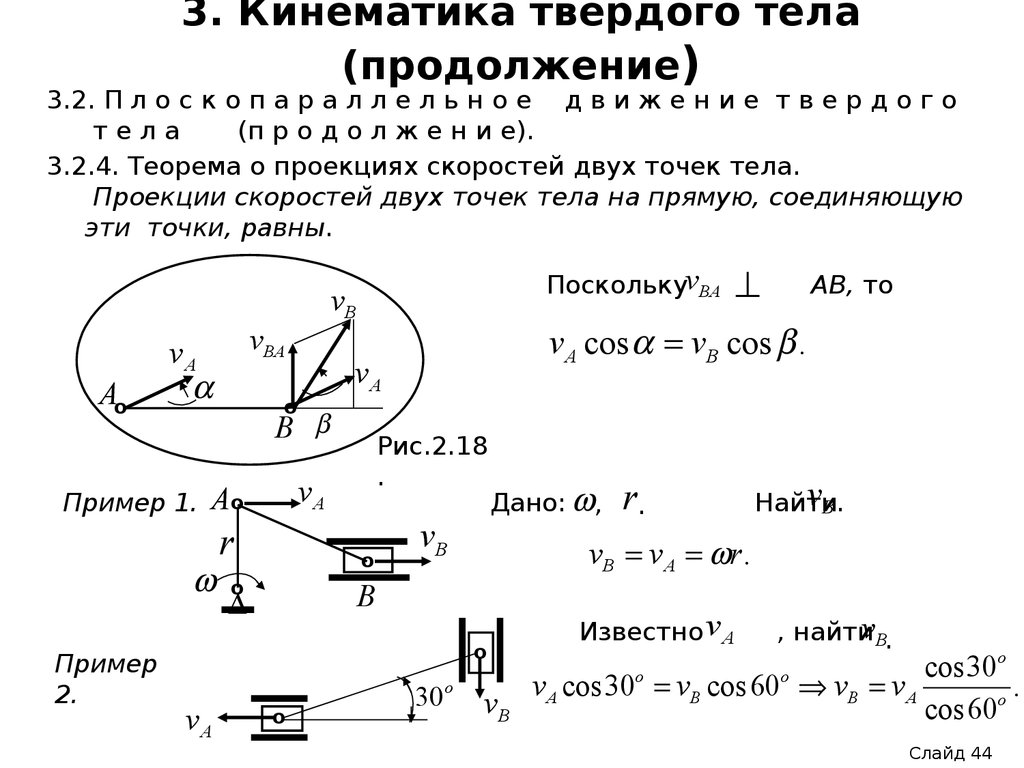
3.2.4. Теорема о проекциях скоростей двух точек тела.
Проекции скоростей двух точек тела на прямую, соединяющую
эти точки, равны.
ПосколькуvBA
vB
vBA
vA
Aо
Пример 1.
Пример
2.
v A cos vB cos .
vA
B
Рис.2.18
.
vА
r
о
о
vB
Дано: ,
B
о
30о
r.
vB .
Найти
v B v А r .
о
vА
АВ, то
о
Aо
Известно v А
cos 30o
v А cos 30 vB cos 60 vB v A
.
o
cos 60
о
vB
, найтиvB.
o
Слайд 44













 physics
physics








