379.50K

Category: $mathematics$ mathematics

Степень и её свойства

Урок 1. Определение
степени с
натуральным показателем. Основное
свойство степени.
Цели и задачи: систематизировать и
углубить знания учащихся, полученные в
5 классе; дать определение степени с
натуральным показателем; формировать
навыки возведения в степень; развивать
самостоятельность учащихся.

3. Устно

• *Как записать в виде произведения 74
• *Найти числовое значение выражения (5)2
• *Чему равно 7 в первой степени?

4.

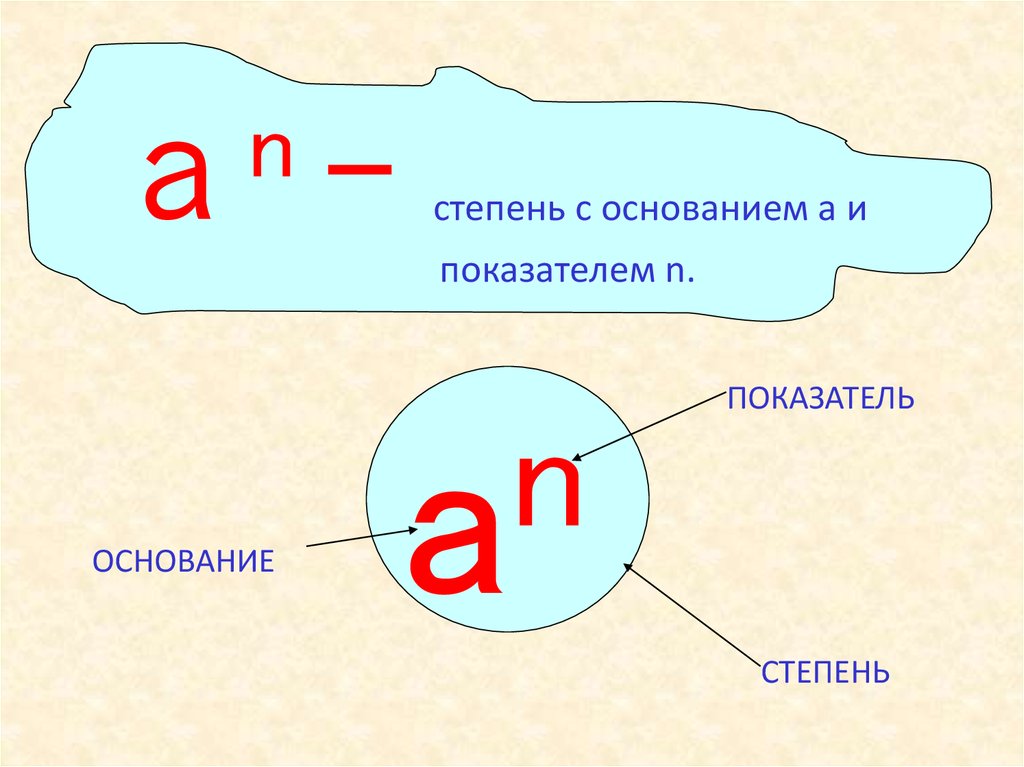
n
а
-
степень с основанием а и
показателем n.
ОСНОВАНИЕ
n
a
ПОКАЗАТЕЛЬ
СТЕПЕНЬ

5.

n
a = a·…·a
n раз
n- натуральное,
а1 = а
n>1

6.

Укажите степени,
их основания и показатели:
5
3,
7
а ,
х
в)2 ,
а)
б)
г)(а + в)2,д)-24,
32
22
е)
, ж)mn , з)
3
(-7) .

7.

Являются ли следующие выражения степенями?
Укажите их основания и показатель.
Поставьте знак «+»,если выражение является степенью,
и знак «-»,если не является.
Выражение
32
(-2) 7
-25
2+35
1 4
6
1
64
Является
степенью
или нет
+
+
+
-
Основание
степени
3
-2
-1
6
-
Показатель
степени
2
7
4
-

8.

Математический диктант.
1. Запишите в виде произведения а 5.
2. Запишите в виде степени ххх.
3. Запишите в виде степени выражение в.
4. Запишите число 2 5 в виде степени числа 5.
5. Найдите числовое значение выражения (-11) 2.
6.Найдите числовое значение квадрата числа
7. Найдите числовое значение куба числа 0,1.
8.Может ли шестая степень какого - нибудь числа быть
отрицательной?
9.Может ли пятая степень числа быть отрицательной?
10.Какое натуральное число в любой степени равно
самому себе?
2
3

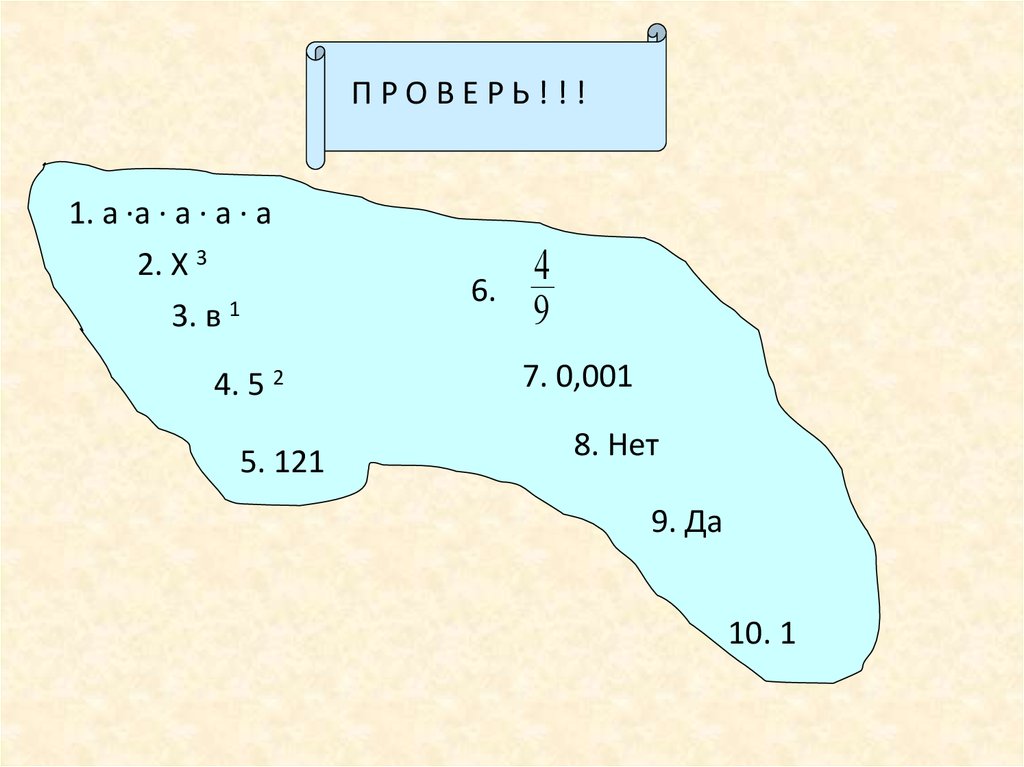
9.

ПРОВЕРЬ!!!
1. а ·а · а · а · а
2. Х 3
3. в 1
4. 5 2
5. 121
6.
4
9
7. 0,001
8. Нет
9. Да
10. 1

10. 3.Закрепление изученного материала

• Выполнить упражнения: №374, №375,
№376(а, в, д, ж, и), №377(а, в, д, ж),
№382, №384.

11. 4. Итог урока

Контрольные вопросы:
-Понятие степени с натуральным показателем.
-Определение основания степени.
-Определение показателя степени.
-Какое число получается при возведении положительного числа в
степень?
• -Какое число получается при возведении нуля в степень?
• -Какое число получается при возведении отрицательного числа в
степень? От чего зависит результат?
• Задание на дом. Пункт 18, №№386-388(1,2 столбики)

12. Урок №2.Действия со степенями.

• Цели и задачи:
• научиться выполнять основные действия
со степенями с натуральными
показателями;
• развивать логическое мышление

13.

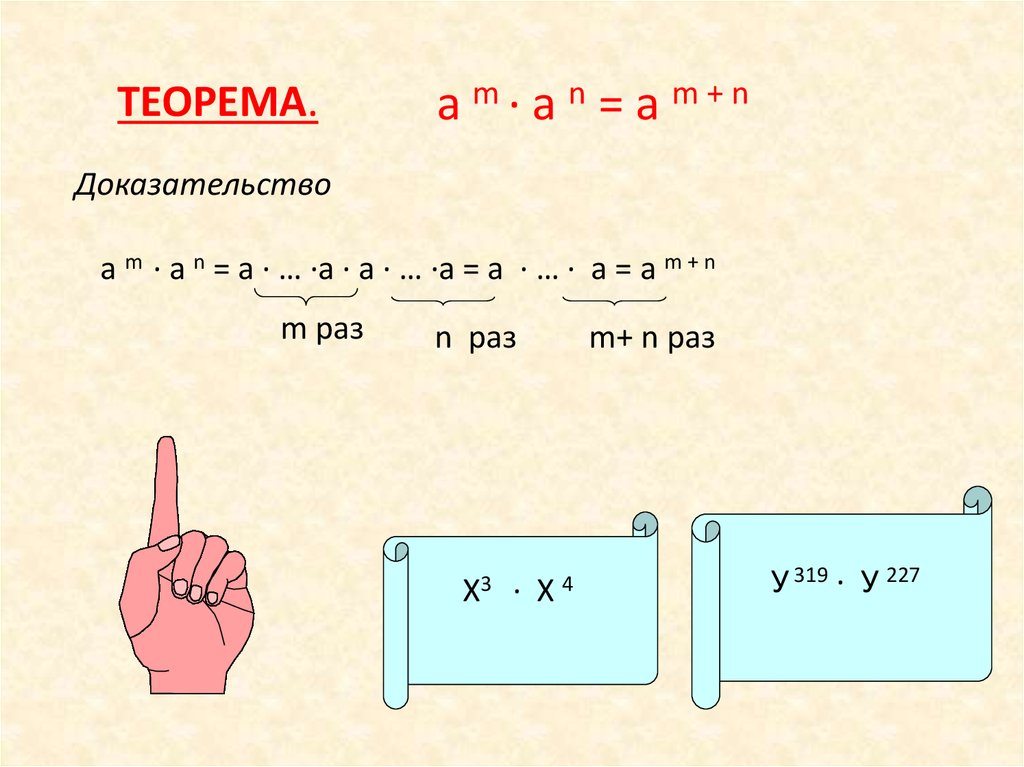
ТЕОРЕМА.
a m· a n = a m+n
Доказательство
a m · a n = a · … ·a · a · … ·a = a · … · a = a m + n
m раз
n раз
Х3 · Х 4
m+ n раз
У 319 · У 227

14.

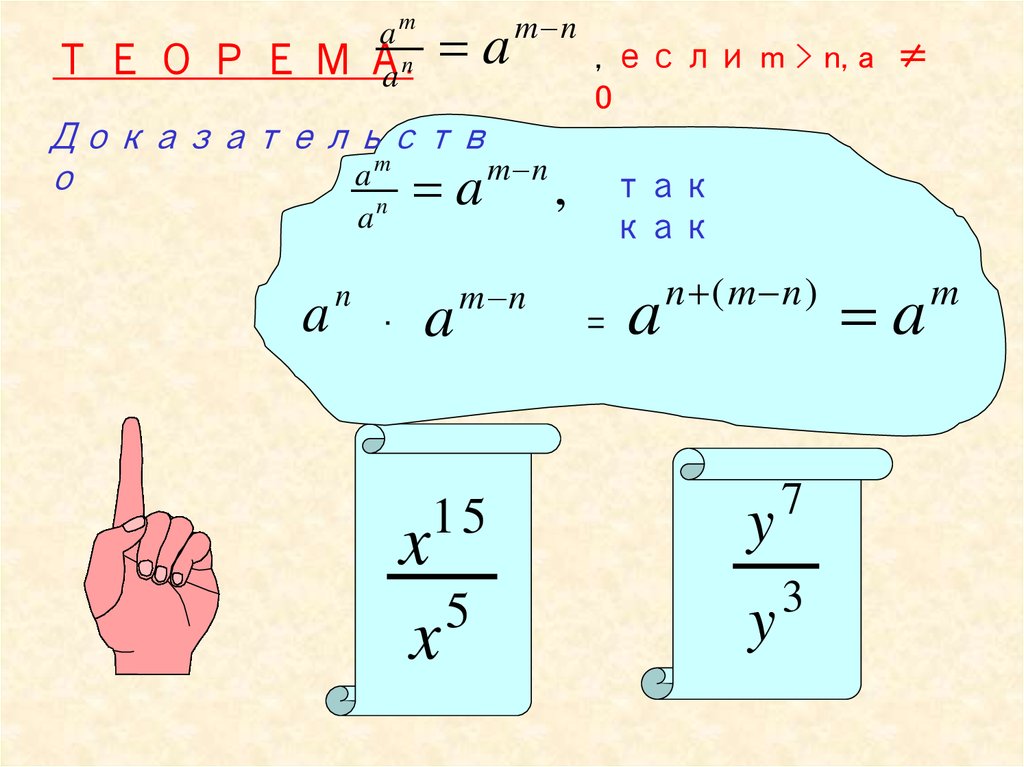
ТЕОРЕМ
am
А.
an
a
m n
, если m > n, a ≠
0
Доказательств
m n
am
о
a ,
a
a
n
так
как
n
·
a
m n
15
x
5
x
=
a
n ( m n )
y
7
y
3
a
m

15.

ТЕОРЕМА.
(a m)n =a mn
Доказательство:
n раз
(a m)n= a m · … · a m = a m + … + m = a m n
n раз
( Х 17) 3, ( У 21) 4

16.

( a b) n=a n b n
ТЕОРЕМА
Доказательство :
(a b) n = ( a b)· … · (ab) = ( a · … · a) · (b · … · b) = a n b n
n раз
n раз
n раз
(2 ·5)3
(ХУ)4

17.

Представьте
выражения в виде
степени с
основанием в:
а)в 4(в 2) 3,
б)(в 4) 5 в 6,
в)( в 3) 7 ( в 5) 3 ,
г) ( в 3) 2 ( в 3)5

18.

РЕШЕНИЕ
в) (
b3)7
a)
b4(b2)3
б)
(b4)5
(b5)3
=
=
b6
=b
21…
…
b b
г)( b3)2 (b3)5 = …b21
b4
6
b
… = … b10
… 20
b6 = …
15 …
=b
36
b26

19.

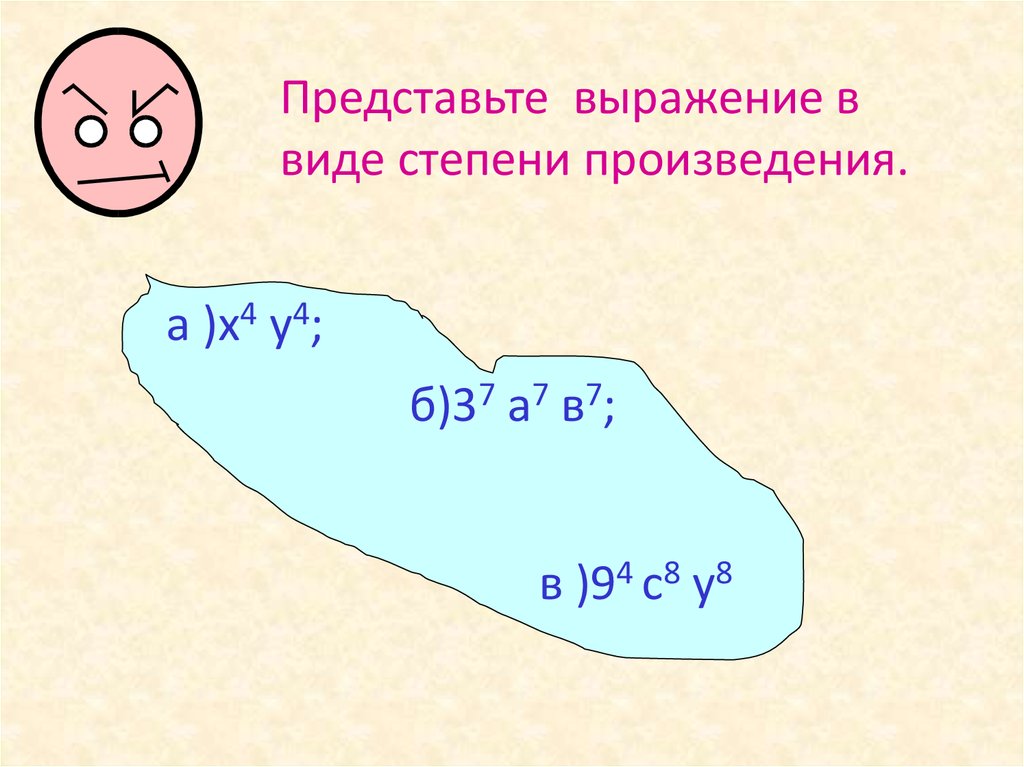
Представьте выражение в
виде степени произведения.
а )х4 у4;
б)37 а7 в7;
в )94 с8 у8

20.

а)x4y4
=(xy
4…
)
б)37a7b7 = (3ab
… )7
в) 94c8y8 =
8
3…c8…
y8
8
= (3cy
… )
…

21.

МАТЕМАТИЧЕСКИЙ
ДИКТАНТ
1). Четвертую степень куба числа 2
представьте в виде степени числа 2.
2 ). Двенадцатую степень числа 2 представьте
в виде квадрата некоторого числа.
3 ). Будет ли правильной дробью степень
правильной дроби?
4 ). Может ли степень числа 22
оканчиваться цифрой 3?
5 ). Запишите в виде степени произведения 23 · 53

27. Домашнее задание

• П.19, 20, №404, №409, №415, №428

English Русский Rules