Similar presentations:
Свойства степени
1.
«Пусть кто-нибудь попробуетвычеркнуть из математики степени,
и он увидит, что без них далеко не уедешь»
М.В.Ломоносов
Как вы думаете, на какие
вопросы мы будем отвечать?
Урок разработал учитель математики
Белова Татьяна Валентиновна
2. Теоретическая разминка
3.
Представьте в виде степени произведение. Назовитеоснование и показатель степени
1. (-8) * (-8) * (-8) * (-8) * (-8) =
2. 4 * 4 * 4 * 4 * 4 * 4 * 4 =
3. C * C* C * …… * C =
10 раз
4.
Найдите значение степени26 =
3
(-5)
=
(-1)7 =
4
-3 =
5.
Выполните действия1) ( - 3)3 =
2) 0,1 * 602 =
2
3) 7 + 7 =
9
3
4)(-1) + 5 =
5) (23)2 =
6) 23 * 25 =
7) 49 : 46 =
8)
6. Изучение нового материала
Как следует выполнять умножение степеней с одинаковымоснованием ?
23
*
32 *
25
34
=
(2 * 2* 2) *(2*2*2*2*2)
= 28
6
3
=
4 * 46 = 47
– Какие результаты вы получили? Подчеркните
начало выражения, его конечный результат.
– Что интересного вы заметили?
7. Умножение степеней с одинаковым основанием
• Для любого числа a и произвольныхнатуральных чисел m и n
am * an = am + n
Правило умножения степеней с одинаковыми основаниями:
При умножении степеней с одинаковыми основаниями основание
оставляют прежним, а показатели степеней складывают.
8. Изучение нового материала
Как следует выполнять деление степеней с одинаковымоснованием ?
47
:
4
4
4 =
4
7
4
3 :3 3
9
6
4*4*4*4*4*4*4
4*4*4= 4 3
4*4*4*4
3
5 : 5 Какие
5 результаты вы получили? Подчеркните
6
4
2
начало выражения, его конечный результат.
– Что интересного вы заметили?
9. Деление степеней с одинаковым основанием
• Для любого числа a 0 и любыхнатуральных чисел m и n, таких, что m > n
am : an = am - n
Правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями основание оставляют
прежним, а из показателя степени делимого вычитают показатель степени
делителя.
10.
При всякомa 0
a :a a
n
n
n n
a 1
0
Степень числа а, не равного нулю, c нулевым
показателем равна единице
3,5
0
1;
5
0
1
11.
12.
Изучение нового материалаКак возвести степень в степень ?
2 2
3 3
5 2
2 3
10
6
Для любого числа а и
натуральных чисел n и k
справедливо равенство
a
n k
a
nk
Правило. При возведении степени в степень показатели
перемножаются
13.
14.
Решаем из учебника15.
Подведем итоги урокаНа уроке мы повторили . . .
На уроке мы узнали . . .
На уроке мы научились . . .
Домашнее задание .












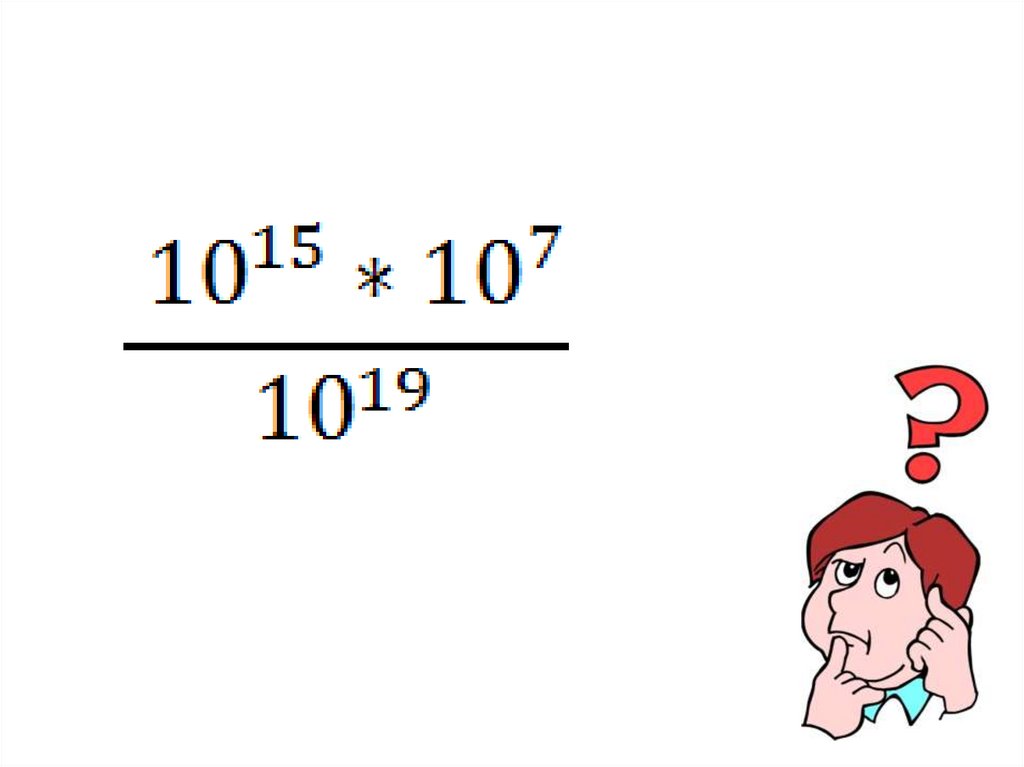



 mathematics
mathematics








